第5章 对函数的再探索章节测评试卷(精选含详解)
文档属性
| 名称 | 第5章 对函数的再探索章节测评试卷(精选含详解) |

|
|
| 格式 | doc | ||
| 文件大小 | 3.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-19 00:00:00 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
九年级数学下册第5章对函数的再探索章节测评
考试时间:90分钟;命题人:数学教研组
考生注意:
1、本卷分第I卷(选择题)和第Ⅱ卷(非选择题)两部分,满分100分,考试时间90分钟
2、答卷前,考生务必用0.5毫米黑色签字笔将自己的姓名、班级填写在试卷规定位置上
3、答案必须写在试卷各个 ( http: / / www.21cnjy.com )题目指定区域内相应的位置,如需改动,先划掉原来的答案,然后再写上新的答案;不准使用涂改液、胶带纸、修正带,不按以上要求作答的答案无效。www.21-cn-jy.com
第I卷(选择题 30分)
一、单选题(10小题,每小题3分,共计30分)
1、下列函数中,自变量x的取值范围是的函数是( )
A. B. C. D.
2、一次函数与反比例函数上的图象在同一直角坐标系下的大致图象如图所示,则、b的取值范围是( )21*cnjy*com
( http: / / www.21cnjy.com / )
A., B., C., D.,
3、下列实际问题中的y与x之间的函数表达式是二次函数的是( )
A.正方体集装箱的体积ym3,棱长xm
B.高为14m的圆柱形储油罐的体积ym3,底面圆半径xm
C.妈妈买烤鸭花费86元,烤鸭的重量y斤,单价为x元/斤
D.小莉驾车以108km/h的速度从南京出发到上海,行驶xh,距上海ykm
4、如图是二次函数图象的一部分,抛物线与轴交点位于与之间,给出四个结论:①,②,③,④,⑤当时,,当时,,则,⑥关于一元二次方程,一定有两个不等的实根,其中正确的有( )【出处:21教育名师】
( http: / / www.21cnjy.com / )
A.2个 B.3个 C.4个 D.5个
5、已知点A(-3,y1),B(2,y2)是反比例函数(k<0)图象上的两点,则有( )
A.y1<y2<0 B.y1<0<y2 C.y2<0<y1 D.y2<y1<0
6、下列关系式中表示是的反比例函数的是( )
A. B. C. D.
7、已知抛物线上部分点的横坐标x纵坐标y的对应值如表:
x … -2 -1 1 3 4 …
y … 2.5 0 -2 0 2.5 …
①物线的开口向上;
②方程的根为-1和3;
③当时,x的取值范围是;
④抛物线的对称轴为直线.
以上结论中正确的是( )
A.①③ B.①②③ C.②④ D.①②④
8、如图,已知抛物线(为常数,)经过点,且对称轴为直线,有下列结论:①;②;③;④无论 取何值,抛物线一定经过.其中正确结论有( )【版权所有:21教育】
( http: / / www.21cnjy.com / )
A.1个 B.2个 C.3个 D.4个
9、如果反比例函数y=的图象经过点(3,﹣4),那么k是( )
A.7 B.10 C.12 D.﹣12
10、小明发现鸡蛋的形状可以近似用抛 ( http: / / www.21cnjy.com )物线与圆来刻画.于是他画了两只鸡蛋的示意图(如图,单位:cm),其中 AB 和 AB 上方为两条开口大小相同的抛物线,下方为两个圆的一部分.若第一个鸡蛋的高度 CD 为 8.4 cm,则第二个鸡蛋的高度 CD 为( )
( http: / / www.21cnjy.com / )
A.7.29 cm B.7.34 cm C.7.39 cm D.7.44 cm
第Ⅱ卷(非选择题 70分)
二、填空题(5小题,每小题4分,共计20分)
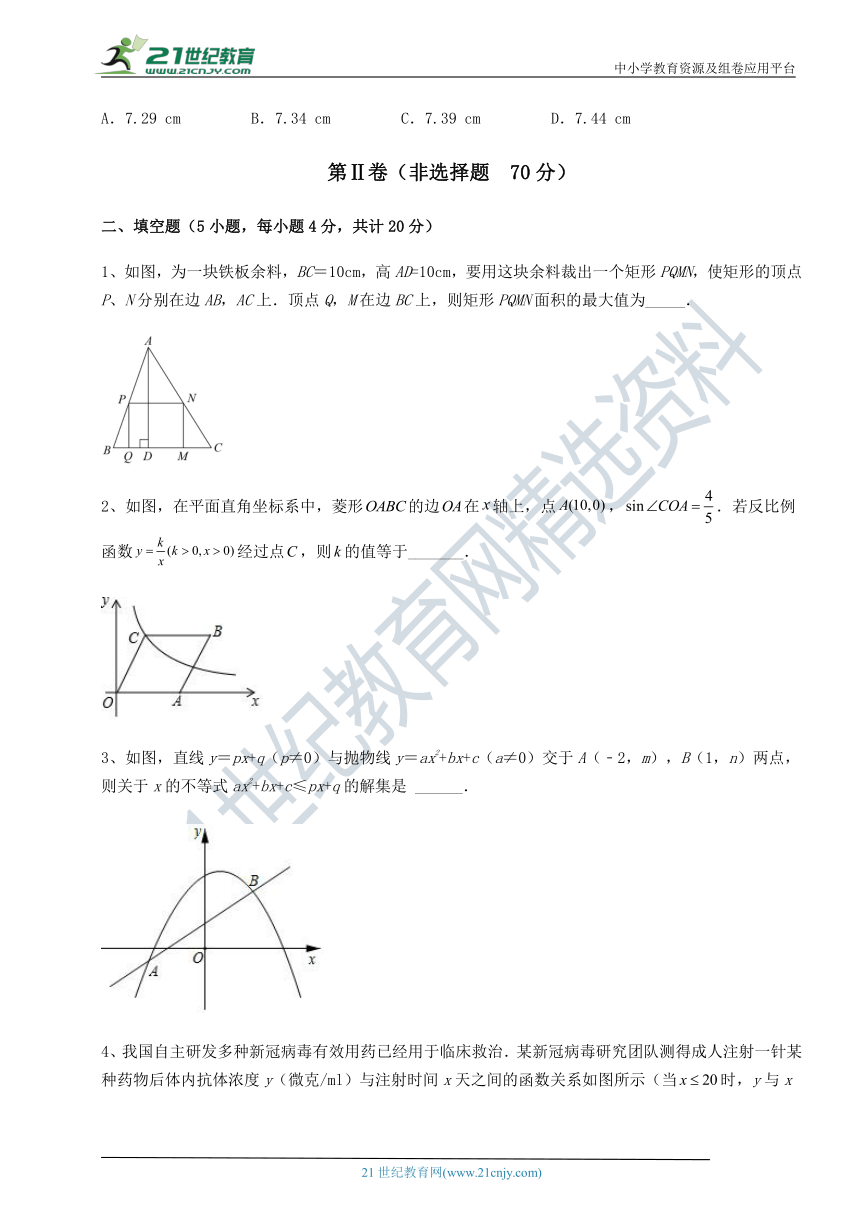
1、如图,为一块铁板余料 ( http: / / www.21cnjy.com ),BC=10cm,高AD=10cm,要用这块余料裁出一个矩形PQMN,使矩形的顶点P、N分别在边AB,AC上.顶点Q,M在边BC上,则矩形PQMN面积的最大值为_____.
( http: / / www.21cnjy.com / )
2、如图,在平面直角坐标系中,菱形的边在轴上,点,.若反比例函数经过点,则的值等于_______.
( http: / / www.21cnjy.com / )
3、如图,直线y=px+q ( http: / / www.21cnjy.com )(p≠0)与抛物线y=ax2+bx+c(a≠0)交于A(﹣2,m),B(1,n)两点,则关于x的不等式ax2+bx+c≤px+q的解集是 ______.
( http: / / www.21cnjy.com / )
4、我国自主研发多种新冠病毒有效用药已经用于临床救治.某新冠病毒研究团队测得成人注射一针某种药物后体内抗体浓度y(微克/ml)与注射时间x天之间的函数关系如图所示(当时,y与x是正比例函数关系;当时,y与x是反比例函数关系).则体内抗体浓度y高于70微克/ml时,相应的自变量x的取值范围是______.
( http: / / www.21cnjy.com / )
5、抛物线y=ax2+bx+c(a,b,c是常数,a<0)的顶点坐标为(1,m),其中m>0.下列四个结论:
①ab<0;
②c>0;
③关于x的一元二次方程ax2﹣bx+c=m+1无实数解;
④点P1(n,y1),P2(3﹣2n,y2)在抛物线上,若n<1,则y1<y2.
其中正确的结论是_____(填写序号).
三、解答题(5小题,每小题10分,共计50分)
1、已知抛物线y=ax2﹣4ax﹣3.
(1)若该抛物线与x轴交于A,B两点,点B在点A(1,0)的右侧,求该抛物线的解析式;
(2)若点P(m,y1),Q(4,y2)在抛物线上,且y1<y2,求m的取值范围.
2、如图,在平面直角坐标系中,四边形是平行四边形,,若、的长是关于的一元二次方程的两个根,且.
( http: / / www.21cnjy.com / )
(1)求、的长.
(2)若点为轴正半轴上的点,且,求经过、两点的直线解析式及经过点的反比例函数的解析式,并判断AOE与AOD是否相似.
(3)若点在平面直角坐标系内,则在直线上是否存在点,使以、、、为顶点且、为邻边的四边形为菱形?若存在,写出点的坐标,若不存在,请说明理由.
3、如图,抛物线与x轴交于A,B两点,与y轴交于C点,连接AC,已知B(﹣1,0),且抛物线经过点D(2,﹣2).
( http: / / www.21cnjy.com / )
(1)求抛物线的表达式;
(2)若点E是抛物线上第四象限内的一点,且,求点E的坐标;
(3)若点P是y轴上一点,以P,A,C三点为顶点的三角形是等腰三角形,求P点的坐标.
4、如图,一次函数yx﹣2的图象与坐标轴交于A,B两点,点C的坐标为(1,0),二次函数y=ax2+bx+c的图象经过A,B,C.
( http: / / www.21cnjy.com / )
(1)求抛物线的解析式;
(2)如图1,已知点D(﹣1,n)在抛物线上,作射线BD,Q为线段AB上一点,过点Q作QM⊥y轴于点M,作QN⊥BD于点N,过点Q作QPy轴交抛物线于点P,交BD于G,当QM与QN的积最大时,求点P的坐标;
(3)如图2,在(2)的条件下,连接AP,若E为抛物线上一点,且满足∠APE=2∠CAO,求点E的坐标.
5、有这样一类特殊边角特征的四边形,它们有“一组邻边相等且对角互补”,我们称之为“等对补四边形”.
( http: / / www.21cnjy.com / )
(1)如图1,四边形ABCD中,∠ ( http: / / www.21cnjy.com )BAD=∠BCD=90°,AD=AB,AE⊥CD于点E,若AE=4,则四边形ABCD的面积等于 .
(2)等对补四边形中,经过 ( http: / / www.21cnjy.com )两条相等邻边的公共顶点的一条对角线,必平分四边形的一个内角,即如图2,四边形ABCD中,AD=DC,∠A+∠C=180°,连接BD,求证:BD平分∠ABC.
(3)现准备在某地著名风景区开 ( http: / / www.21cnjy.com )发一片国家稀有动物核心保护区,保护区的规划图如图3所示,该地规划部门要求:四边形ABCD是一个“等对补四边形”,满足AD=DC,AB+AD=12,∠BAD=120°,因地势原因,要求3≤AD≤6,求该区域四边形ABCD面积的最大值.
-参考答案-
一、单选题
1、B
【解析】
【分析】
根据被开方数大于等于0,分母不等于0对各选项分别列式计算即可得解.
【详解】
解:A.中x≥1,此选项不符合题意;
B.中x>1,此选项符合题意;
C.中x≥,此选项不符合题意;
D.中x≥2,此选项不符合题意;
故答案选:B.
【点睛】
本题考查了函数自变量的范 ( http: / / www.21cnjy.com )围,一般从三个方面考虑:当函数表达式是整式时,自变量可取全体实数;当函数表达式是分式时,考虑分式的分母不能为0;当函数表达式是二次根式时,被开方数非负.
2、D
【解析】
【分析】
本题根据题意,判断一次函数和反比例函数的图象在哪个象限,即可判断的正负.
【详解】
反比例函数经过二、四象限,
,
一次函数经过二、三、四象限,
,
,
故选:D.
【点睛】
本题主要考查一次函数和反比例函数图象的性质,根据图象判断的正负是解题的关键.
3、B
【解析】
【分析】
根据二次函数的定义逐项判断即可.
【详解】
解:A.正方体集装箱的体积ym3,棱长xm,则y=x3,故不是二次函数;
B.高为14m的圆柱形储油罐的体积ym3,底面圆半径xm,则y=14πx2,故是二次函数;
C.妈妈买烤鸭花费86元,烤鸭的重量y斤,单价为x元/斤,则,故不是二次函数;
D.小莉驾车以108km/h的速度从南京出发到上海,行驶xh,距上海ykm,则y=南京与上海之间的距离-108x,故不是二次函数.21世纪教育网版权所有
故选:B.
【点睛】
本题考查二次函数的定义,解答本题的关键是明确题意,写出相应的函数解析式,利用二次函数的定义去判断.
4、A
【解析】
【分析】
由抛物线开口方向,对称轴位置,抛物 ( http: / / www.21cnjy.com )线与y轴交点位置可判断①,由抛物线对称轴和抛物线经过(﹣1,0)可得抛物线经过(3,0),从而可得b,c与a的关系,进而判断②,由x=﹣2时y<0可判断③,由x=1时y取最大值可判断④,由抛物线开口向下,对称轴为直线x=1可判断⑤,将ax2+bx+c﹣5=0化为只含系数a的方程,根据根与判别式的关系可判断⑥.21·cn·jy·com
【详解】
解:∵抛物线开口向下,
∴a<0,
∵抛物线对称轴为直线x=﹣=1,
∴b=﹣2a>0,
∵抛物线与y轴交点在x轴上方,
∴c>0,
∴abc<0,①正确.
∵抛物线经过点(﹣1,0),抛物线对称轴为直线x=1,
∴抛物线经过(3,0),
∴a﹣b+c=0,9a+3b+c=0,
∴10a+2b+2c=0,
∵b=﹣2a,
∴a=﹣,
∴﹣5b+2b+2c=﹣3b+2c=0,
∴b=c,
∴ c=b
∵抛物线与y轴交点位于(0,2)与(0,3)之间,
∴2<c<3,
∴2<b<3,
∴<b<2,②错误.
∵x=﹣2时,y<0,
∴4a﹣2b+c<0,③正确.
∵x=1时,y取最大值,
∴a+b+c≥am2+bm+c,
∴a+b≥am2+bm,④错误.
∵抛物线开口向下,2.5﹣1<1﹣(﹣2.5)
∴y1<y2,⑤错误.
∵b=c=﹣2a,
∴c=﹣3a,a=﹣c,
∵ 2<c<3
∴﹣1<﹣c<﹣
∴﹣1<a<﹣,
由ax2+bx+c﹣5=0可得ax2﹣2ax﹣3a﹣5=0,
∵﹣4<4a<﹣,1<4a +5<
∴Δ=(﹣2a)2﹣4a(﹣3a﹣5)=16a2+20a=4a(4a+5)<0,
∴方程ax2+bx+c﹣5=0无实数根,⑥错误.
故①③ 正确
故选:A.
【点睛】
本题考查二次函数图象与系数的关系,解题关键是掌握二次函数与方程及不等式的关系.
5、C
【解析】
【分析】
由反比例函数(k<0),可得 即函数图象分布在二,四象限,再结合点A(-3,y1),B(2,y2)是反比例函数(k<0)图象上的两点,判断的位置即可得到答案.
【详解】
解: 反比例函数(k<0),
即函数图象分布在二,四象限,
点A(-3,y1),B(2,y2)是反比例函数(k<0)图象上的两点,
故选C
【点睛】
本题考查的是反比例函数的图象与性质,掌握“当时,反比例函数的图象分布在第二,第四象限”是解本题的关键.2·1·c·n·j·y
6、A
【解析】
【分析】
根据反比例函数定义:形如的函数是反比例函数,即可得到答案.
【详解】
解:A、是反比例函数,故本选项符合题意;
B、是一次函数,故本选项不符合题意;
C、是二次函数,故本选项不符合题意;
D、是正比例函数,故本选项不符合题意;
故选A.
【点睛】
本题考查了反比例函数的定义,熟记正比例函数,反比例函数以及一次函数、二次函数的定义是解题的关键,是基础题,难度不大.【来源:21·世纪·教育·网】
7、B
【解析】
【分析】
先利用待定系数法求出抛物线解 ( http: / / www.21cnjy.com )析式,确定a的符号可判断①,利用函数值为0的两点横坐标为方程的解可判断②,利用图像解不等式确定自变量的取值范围可判断③,利用对称两的坐标可求对称轴可判断④.
【详解】
解:把(-2,2.5),(-1,0),(1,-2)代入抛物线解析式得:
,
解方程组得,
∴,
∴a=0.5>0,抛物线开口向上,故①正确;
∵(-1,0)和(3,0)在抛物线上,
∴当x=-1时,当x=3时,故②正确;
∵抛物线与x轴的交点坐标为(-1,0)和(3,0),
当时,函数图像在x轴下方,在两交点之间,x的取值范围是,故③正确;
∵抛物线的对称两点坐标为(-2,2.5),(4,2.5),
∴抛物线的对称轴为x=,故④不正确,
故正确的答案为①②③;
故选B.
( http: / / www.21cnjy.com / )
【点睛】
本题考查从表格获取信息与处理信息,待定系数 ( http: / / www.21cnjy.com )法求抛物线解析式确定抛物线性质,抛物线与x轴的交点的意义,利用图像与表格解不等式,确定自变量取值范围.
8、C
【解析】
【分析】
由题意得到抛物线的开口向上,对称轴﹣=,判断a,b与0的关系,即可判断①;根据抛物线对称轴方程可得a+b=0,即可判断②;根据抛物线y=ax2+bx+c经过点(2,0)以及c<0,得到4a+2b+3c<0,即可判断③;先根据a+b=0和4a+2b+c=0得c=﹣2a,再根据对称性可知:抛物线过(﹣1,0),即可判断④.【来源:21cnj*y.co*m】
【详解】
解:①∵抛物线开口向上,
∴a>0,
抛物线的对称轴为直线x=,即﹣=,,
∴b<0,故①正确;
②∵,
∴a+b=0,
故②不正确;
③∵抛物线y=ax2+bx+c(a,b,c为常数,a≠0)经过点(2,0),
∴4a+2b+c=0,
抛物线与y轴交点在负半轴,所以c<0,
∴4a+2b+3c<0,
故③正确;
④由对称得:抛物线与x轴另一交点为(﹣1,0),
∵,
∴c=﹣2a,
∴=﹣1,
∴无论a,b,c取何值,抛物线一定经过(,0),
故④正确;
本题正确的有:①③④,共3个.
故选:C.
【点睛】
本题考查了二次函数图象与系数的关系:对于 ( http: / / www.21cnjy.com )二次函数y=ax2+bx+c(a≠0),二次项系数a决定抛物线的开口方向和大小:当a>0时,抛物线向上开口;当a<0时,抛物线向下开口;一次项系数b和二次项系数a共同决定对称轴的位置:当a与b同号时(即ab>0),对称轴在y轴左;当a与b异号时(即ab<0),对称轴在y轴右;常数项c决定抛物线与y轴交点位置:抛物线与y轴交于(0,c).21教育网
9、D
【解析】
【分析】
直接把点(3,﹣4)代入反比例函数y=即可得出k的值.
【详解】
解:∵反比例函数y=的图象经过点(3,﹣4),
∴-4=,
解得k=-12.
故选D.
【点睛】
本题考查的是反比例函数图象上点的坐标特点,熟知反比例函数图象上各点的坐标一定适合此函数的解析式是解答此题的关键.www-2-1-cnjy-com
10、A
【解析】
【分析】
在图1中,由锐角三角函数求出AE长,以AB所在直线为x轴,CD所在直线为y轴,设抛物线的解析式为:y=ax2+3,进而求出a值,同理在图2中, A B 所在直线为x轴,C D 所在直线为y轴,设抛物线的解析式为:y=x2+b ,求出b ,即可得到C E ,由C D =C E +O E +O D 即可得解.
【详解】
解:如图1,
( http: / / www.21cnjy.com / )
在Rt△AOE中, AO=BO=3.6,∠AOE=60 ,
∴OE=OAsin60 =3.6×=1.8,AE= OAcos60 =3.6×=,
以AB所在直线为x轴,CD所在直线为y轴,
设抛物线的解析式为:y=ax2+3,
当x=时,y=a×()2+3=0,
∴a=,
如图2,
( http: / / www.21cnjy.com / )
在Rt△A O E 中, A O =B O =3.24,∠A O E =60 ,
∴O E =O A cos60 =3.24×=1.62,A E = O A sin60 =3.24×=,
以A B 所在直线为x轴,C D 所在直线为y轴,
设抛物线的解析式为:y=x2+b ,
当x=时,y=×()2+b =0,
∴b =2.43,即C E =2.43,
∴C D =C E +O E +O D =2.43+1.62+3.24=7.29cm.
故选:A
【点睛】
此题考查了待定系数法求二次函数解析式,锐角三角函数,建立适当的坐标系求二次函数解析式是解答此题的关键.
二、填空题
1、25
【解析】
【分析】
设DE=x,根据矩形的性质得到,PQ=MN=DE,证明△APN∽△ABC,得到,求出PN=10-x得到矩形的面积,根据二次函数的性质求解.
【详解】
解:设DE=x,
∵四边形PQMN是矩形,AD⊥BC,
∴,PQ=MN=DE,
∴△APN∽△ABC,
∴,
∴,
∴PN=10-x,
∴矩形PQMN面积=,
∴当x=5时,矩形PQMN面积有最大值,最大值为25cm2,
故答案为:25.
( http: / / www.21cnjy.com / ).
【点睛】
此题考查了矩形的性质,相似三角形的判定及性质,二次函数的最值,正确掌握相似三角形的判定及性质定理是解题的关键.
2、48
【解析】
【分析】
由菱形的性质和锐角三角函数可求点,将点坐标代入解析式可求的值.
【详解】
解:如图,过点作于点,
( http: / / www.21cnjy.com / )
菱形的边在轴上,点,
,
.
,
,
点坐标,
反比例函数经过点,
,
故答案为:48.
【点睛】
本题考查了反比例函数性质,反比例函数图象上点的坐标特征,菱形的性质,锐角三角函数,解题的关键是求出点坐标.
3、x≤﹣2或x≥1##x≥1或x≤﹣2
【解析】
【分析】
直接利用函数的交点坐标进而结合函数图象得出不等式ax2+bx+c≤px+q的解集.
【详解】
解:由图象可得点A左侧与点B右侧抛物线在直线下方,
∴x≤﹣2或x≥1时,ax2+bx+c≤px+q,
故答案为:x≤﹣2或x≥1.
【点睛】
此题主要考查了二次函数与不等式,正确数形结合分析是解题关键.
4、
【解析】
【分析】
根据函数图像求得正比例函数和反比例函数,进而根据题意求得时的自变量x的取值范围.
【详解】
解:根据题意设时,正比例函数为,时,反比例函数为,将点代入,得
,
当时,当时,
当时,当时,
根据函数图像可知,则体内抗体浓度y高于70微克/ml时,相应的自变量x的取值范围是
故答案为:
【点睛】
本题考查了正比例函数和反比例函数的应用,从函数图象获取信息是解题的关键.
5、①③##③①
【解析】
【分析】
①根据顶点的横坐标推出b=﹣2a,则ab=﹣2a2<0即可判断;
②当抛物线与x轴的交点都在x轴正半轴,则抛物线交y轴负半轴时,此时c<0先即可判断②;
③根据二次函数的性质,抛物线y=ax2+bx+c与直线y=m+1无交点,即可判断③;
③根据二次函数图象上点的坐标特征即可判断④.
【详解】
解:①∵抛物线y=ax2+bx+c(其中a,b,c是常数,m),
∴﹣=1,
∴b=﹣2a,
∴ab=﹣2a2<0,故①正确;
②由题意可知抛物线开口向下,对称轴为直线x=1,顶点坐标为(1,m),其中m>0
∴抛物线与x轴有两个交点,
当抛物线与x轴的交点在x轴正半轴,则抛物线交y轴负半轴时,故②错误;
③∵抛物线y=ax2+bx+c开口向下,函数有最大值m,
∴抛物线y=ax2+bx+c与直线y=m+1无交点,
∴关于x的一元二次方程ax2﹣bx+c=m+1无实数解,故③正确;
④抛物线y=ax2+bx+c开口向下,点P1(n,y1),P2(3﹣2n,y2)在抛物线上,
若n<1,则1﹣n<3﹣2n﹣1,
∴y1>y2.故④错误;
故答案为①③.
【点睛】
本题主要考查了二次函数图象与二次函数的系数的关系,解决本题的关键是二次函数的性质和一元二次方程与二次函数的关系.
三、解答题
1、 (1)y=-x2+4x﹣3;
(2)当a>0时00时m<0或m>4
【解析】
【分析】
(1)将点A代入解析式计算即可求出a,得到函数解析式;
(2)求出函数的对称轴,根 ( http: / / www.21cnjy.com )据对称性得到与点Q(4,y2)关于直线x=2对称的点的坐标为(0,y2),再分两种情况①当a>0时,②当a>0时,分别求出答案.21·世纪*教育网
(1)
解:将点A代入y=ax2﹣4ax﹣3,得a-4a-3=0,
解得a=-1,
∴该抛物线的解析式为y=-x2+4x﹣3;
(2)
解:∵抛物线的对称轴为直线,
∴与点Q(4,y2)关于直线x=2对称的点的坐标为(0,y2),
分两种情况:
①当a>0时,由y1<y2,得0②当a>0时,由y1<y2,得m<0或m>4.
【点睛】
此题考查了求二次函数的解析式,二次函数的性质,分类讨论解决问题,正确理解二次函数的对称性是解题的关键.21*cnjy*com
2、 (1),
(2),,
(3)存在,,
【解析】
【分析】
(1)根据题意解一元二次方程即可;
(2)根据题意,设,根据求得的坐标,进而根据平行四边形的性质求得点的坐标,从而求得直线解析式;根据在反比例函数图象上求得反比例函数解析式;计算可得,根据夹角相等即可证明AOE与AOD相似;
(3)根据,又,可得平分,分二种情况考虑:①、是邻边;②、是邻边,进而根据菱形的性质求得点的坐标即可.
(1)
方程,分解因式得:,可得:,,
解得:,,
∵,
∴,;
(2)
根据题意,设,
则,
解得:,
∴,
∵四边形是平行四边形,
∴点的坐标是,
设经过、两点的直线的解析式为,
则,
解得:,
∴解析式为;
设反比例函数解析式为,把代入得:,
∴反比例函数解析式为;
在与中,
,,
∴,
又∵,
∴;
( http: / / www.21cnjy.com / )
(3)
根据计算的数据,,
∵,
∴平分,
分二种情况考虑:
①、是邻边,点在射线上时,,
∴点与重合,即;
②、是邻边,点在射线上时,应在直线上,且垂直平分,根据,,
∴此时点坐标为;
综上所述,满足条件的点有二个:;
( http: / / www.21cnjy.com / )
【点睛】
此题考查了解一元二次方程,相似三角形的性质与判定,待定系数法求函数解析式,综合性较强,求点要根据与是邻边的情况进行讨论,不要漏解.
3、 (1)
(2)E(,-1)
(3)P点的坐标(0,2)或(0,﹣2)或(0,﹣2﹣)或(0,)
【解析】
【分析】
(1)用待定系数法求解即可,将坐标代入表达式得解.
(2)欲求三角形得面积,通过A、B两点得坐 ( http: / / www.21cnjy.com )标,我们很轻松得得到AB得长度,同时E点纵坐标的绝对值就是新三角形的高,三角形的面积为2,通过面积公式,便可得解.因为抛物线的对称性,我们可以找到两个横坐标,又因为E点在第四象限,所以横坐标为正数,此题可解.
(3)如图2,设P(0,m),则PC =m+2,OA =3.根据勾股定理得到. ①当PA=CA时,则OP1= OC=2.②当PC = CA=时,可得即m+2=,解方程即可求解.③当PC= CA= 时,可得m=-2-, 于是得到结论.④当PC=PA时,点P在AC的垂直平分线上,根据相似三角形性质得到.
(1)
把B(﹣1,0),D(2,﹣2)
代入中,得
,
解得:.
∴ 抛物线的表达式为;
(2)
当y=0时,,
解得x1=﹣1,x2=3,
∴A(3,0),
∴AB=4,
如图1,过点E作x轴的垂线交x轴于点D,连接AE,BE.
设点点E(t,),其中0<t<3,
∴
∴,
解得,(舍去).
此时,
∴E(,-1).
( http: / / www.21cnjy.com / )
(3)
在中,当x=0时,y=﹣2,
∴C(0,﹣2)
∴OC=2,
如图2,设P(0,m),则PC=m+2,OA=3,AC=,
①当PA=CA时,则OP1=OC=2,
∴P1(0,2)
②当PC=CA=时,即m+2=,
∴m=﹣2,
∴P2(0,﹣2)
③当PC=CA=时,
,
m=﹣2﹣,
∴P3(0,﹣2﹣).
④当PC=PA时,点P在AC的垂直平分线上,
则△AOC∽△P4FC,
∴
∴
∴P4C=,
∴,
∴P4(0,),
综上所述,P点的坐标(0,2)或(0,﹣2)或(0,﹣2﹣)或(0,).
( http: / / www.21cnjy.com / )
【点睛】
本题考察了二次函数的综合题,涉 ( http: / / www.21cnjy.com )及待定系数法求函数解析式,等腰三角形的判定和性质,三角形的面积公式,利用相似三角形的比例建立表达式,正确地作出辅助线也是解题的关键.
4、 (1)y2;
(2)P(﹣2,﹣3);
(3)E(10,63)
【解析】
【分析】
(1)先求出点A、B的坐标,再利用待定系数法求解二次函数解析式即可;
(2)延长PQ交OB于H,延长NQ交OB于K,作DE⊥OB于E,先求得点D坐标,设Q(m,m﹣2),根据坐标与图形性质,先判断出△KNB和△KHQ为等腰直角三角形,再根据等腰直角三角形的性质表示出QN=NK﹣QK (m+6)(),进而有QM QN=﹣m ((m+2)2,然后根据二次函数的性质求解即可;21教育名师原创作品
(3)作PI⊥OA于I,在射线AI上截取IJ=IA,作∠APK=∠APJ交y轴于K,根据点P坐标可得AI=OC=1,PI=OA=2,进而可求得直线PJ的解析式是:y,与抛物线解析式联立,由得此时点E不存在,故作KT∥PJ交PA的延长线于T,利用角平分线的性质作AL⊥PJ于L,作AS⊥PK于S,求得AS=AL,PS=PL,进而在Rt△AKS中,利用勾股定理求解m值,进而求得点K的坐标,求出直线PK的解析式,与抛物线解析式联立方程组求解即可解答.
(1)
解:当y=0时,由x﹣2=0得:x=﹣4,
∴B(﹣4,0),
当x=0时,y=﹣2,
∴A(0,﹣2),
∴设抛物线的解析式是y=a(x+4)·(x﹣1),
∴a×4×(﹣1)=﹣2,
∴a,
∴y(x+4)·(x﹣1)2;
(2)
解:如图1,
( http: / / www.21cnjy.com / )
延长PQ交OB于H,延长NQ交OB于K,作DE⊥OB于E,
由题意得,n2=﹣3,
∴D(﹣1,﹣3),
∴DE=BE=3,
∴∠DBE=45°,
∴△KNB和△KHQ是等腰直角三角形,
设Q(m,m﹣2),
∴QM=﹣m,
HK=QH,
BH=m+4,
QK HK (),
BK=BH+HK,
∴NK BK (m+6),
∴QN=NK﹣QK
(m+6)()
,
∴QM QN=﹣m (
(m+2)2,
∴当m=﹣2时,QM QN最大,
∴当m=﹣2时,y(﹣2+4)×(﹣2﹣1)=﹣3,
∴P(﹣2,﹣3);
(3)
解:如图2,
( http: / / www.21cnjy.com / )
作PI⊥OA于I,在射线AI上截取IJ=IA,作∠APK=∠APJ交y轴于K,
∴PA=PJ,
∴∠APJ=2∠API,
∵P(﹣2,﹣3),A(0,﹣2),C(1,0),
∴AI=OC=1,PI=OA=2,
∴Rt△API≌Rt△CAO(SAS),
∴∠API=∠CAO,
∴∠APJ=2∠CAO,
∵P(﹣2,﹣3),J(0,﹣4),
∴直线PJ的解析式是:y,
由得,
∴x1=x2=﹣2,
∴此时点E不存在
作KT∥PJ交PA的延长线于T,
∴∠T=∠APJ=∠APK,,
即,
∴PK=KT,设KTm,AK=2m,
∴PKm,
作AL⊥PJ于L,作AS⊥PK于S,
∴AS=AL,PS=PL,
∵S△APJ,
∴ AL=2×2,
∴AS=AL,
∴PS=PL,
在Rt△AKS中,AK=2m,AS,SK=PK﹣PS,
∴()2+()2=(2m)2
∴m1=5,m2=1(舍去),
∴AK=2m=10,
∴K(0,8),
∴直线PK的解析式是:y,
由2得,
∴x1=10,x2=﹣2(舍去)
当x=10时,y63,
∴E(10,63).
【点睛】
本题考查二次函数的综合,涉及待 ( http: / / www.21cnjy.com )定系数法求二次函数解析式和一次函数的解析式、一次函数的图象与性质、等腰直角三角形的性质、解直角三角形、二次函数的最值、坐标与图形、全等三角形的判定与性质、勾股定理、解一元二次方程等知识,综合性强,难度困难,属于中考压轴题型,添加适当的辅助线,利用数形结合思想进行求解是解答的关键.21cnjy.com
5、 (1)9
(2)见解析
(3)
【解析】
【分析】
(1)过作,交的延长线于,求出四边形是矩形,根据矩形的性质得出,求出,根据得出,根据全等得出,,求出,求出,代入求出即可;2-1-c-n-j-y
(2)如图1中,连接,.证明,,,四点共圆,利用圆周角定理即可解决问题.
(3)如图3中,延长到,使得,连接,过点作于,根点作于,于.设.构建二次函数,利用二次函数的性质即可解决问题.
(1)
解:如图1,过作,交的延长线于,
( http: / / www.21cnjy.com / )
,
,
四边形是矩形,
,
,
,
在和中,
,
,
,,
四边形是矩形,
四边形是正方形,
,
.
故答案为:16;
(2)
解:证明:如图2中,连接.
( http: / / www.21cnjy.com / )
,
,,,四点共圆,
,
,
,
平分.
(3)
解:如图3中,延长到,使得,连接,过点作于,过点作于,于.设.
( http: / / www.21cnjy.com / )
,,
,
,
,
是等边三角形,
,
,
由(2)可知.平分,
,
,
,
,,
,,
,
,
,,
,
,
时,有最大值,最大值.
【点睛】
本题属于四边形综合题,考查了“邻等对补四边形 ( http: / / www.21cnjy.com )”的定义,解直角三角形,等边三角形的判定和性质,四点共圆,二次函数的应用等知识,解题的关键是理解题意,灵活运用所学知识解决问题,学会利用参数构建二次函数,利用二次函数的性质解决最值问题,属于中考压轴题.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
九年级数学下册第5章对函数的再探索章节测评
考试时间:90分钟;命题人:数学教研组
考生注意:
1、本卷分第I卷(选择题)和第Ⅱ卷(非选择题)两部分,满分100分,考试时间90分钟
2、答卷前,考生务必用0.5毫米黑色签字笔将自己的姓名、班级填写在试卷规定位置上
3、答案必须写在试卷各个 ( http: / / www.21cnjy.com )题目指定区域内相应的位置,如需改动,先划掉原来的答案,然后再写上新的答案;不准使用涂改液、胶带纸、修正带,不按以上要求作答的答案无效。www.21-cn-jy.com
第I卷(选择题 30分)
一、单选题(10小题,每小题3分,共计30分)
1、下列函数中,自变量x的取值范围是的函数是( )
A. B. C. D.
2、一次函数与反比例函数上的图象在同一直角坐标系下的大致图象如图所示,则、b的取值范围是( )21*cnjy*com
( http: / / www.21cnjy.com / )
A., B., C., D.,
3、下列实际问题中的y与x之间的函数表达式是二次函数的是( )
A.正方体集装箱的体积ym3,棱长xm
B.高为14m的圆柱形储油罐的体积ym3,底面圆半径xm
C.妈妈买烤鸭花费86元,烤鸭的重量y斤,单价为x元/斤
D.小莉驾车以108km/h的速度从南京出发到上海,行驶xh,距上海ykm
4、如图是二次函数图象的一部分,抛物线与轴交点位于与之间,给出四个结论:①,②,③,④,⑤当时,,当时,,则,⑥关于一元二次方程,一定有两个不等的实根,其中正确的有( )【出处:21教育名师】
( http: / / www.21cnjy.com / )
A.2个 B.3个 C.4个 D.5个
5、已知点A(-3,y1),B(2,y2)是反比例函数(k<0)图象上的两点,则有( )
A.y1<y2<0 B.y1<0<y2 C.y2<0<y1 D.y2<y1<0
6、下列关系式中表示是的反比例函数的是( )
A. B. C. D.
7、已知抛物线上部分点的横坐标x纵坐标y的对应值如表:
x … -2 -1 1 3 4 …
y … 2.5 0 -2 0 2.5 …
①物线的开口向上;
②方程的根为-1和3;
③当时,x的取值范围是;
④抛物线的对称轴为直线.
以上结论中正确的是( )
A.①③ B.①②③ C.②④ D.①②④
8、如图,已知抛物线(为常数,)经过点,且对称轴为直线,有下列结论:①;②;③;④无论 取何值,抛物线一定经过.其中正确结论有( )【版权所有:21教育】
( http: / / www.21cnjy.com / )
A.1个 B.2个 C.3个 D.4个
9、如果反比例函数y=的图象经过点(3,﹣4),那么k是( )
A.7 B.10 C.12 D.﹣12
10、小明发现鸡蛋的形状可以近似用抛 ( http: / / www.21cnjy.com )物线与圆来刻画.于是他画了两只鸡蛋的示意图(如图,单位:cm),其中 AB 和 AB 上方为两条开口大小相同的抛物线,下方为两个圆的一部分.若第一个鸡蛋的高度 CD 为 8.4 cm,则第二个鸡蛋的高度 CD 为( )
( http: / / www.21cnjy.com / )
A.7.29 cm B.7.34 cm C.7.39 cm D.7.44 cm
第Ⅱ卷(非选择题 70分)
二、填空题(5小题,每小题4分,共计20分)
1、如图,为一块铁板余料 ( http: / / www.21cnjy.com ),BC=10cm,高AD=10cm,要用这块余料裁出一个矩形PQMN,使矩形的顶点P、N分别在边AB,AC上.顶点Q,M在边BC上,则矩形PQMN面积的最大值为_____.
( http: / / www.21cnjy.com / )
2、如图,在平面直角坐标系中,菱形的边在轴上,点,.若反比例函数经过点,则的值等于_______.
( http: / / www.21cnjy.com / )
3、如图,直线y=px+q ( http: / / www.21cnjy.com )(p≠0)与抛物线y=ax2+bx+c(a≠0)交于A(﹣2,m),B(1,n)两点,则关于x的不等式ax2+bx+c≤px+q的解集是 ______.
( http: / / www.21cnjy.com / )
4、我国自主研发多种新冠病毒有效用药已经用于临床救治.某新冠病毒研究团队测得成人注射一针某种药物后体内抗体浓度y(微克/ml)与注射时间x天之间的函数关系如图所示(当时,y与x是正比例函数关系;当时,y与x是反比例函数关系).则体内抗体浓度y高于70微克/ml时,相应的自变量x的取值范围是______.
( http: / / www.21cnjy.com / )
5、抛物线y=ax2+bx+c(a,b,c是常数,a<0)的顶点坐标为(1,m),其中m>0.下列四个结论:
①ab<0;
②c>0;
③关于x的一元二次方程ax2﹣bx+c=m+1无实数解;
④点P1(n,y1),P2(3﹣2n,y2)在抛物线上,若n<1,则y1<y2.
其中正确的结论是_____(填写序号).
三、解答题(5小题,每小题10分,共计50分)
1、已知抛物线y=ax2﹣4ax﹣3.
(1)若该抛物线与x轴交于A,B两点,点B在点A(1,0)的右侧,求该抛物线的解析式;
(2)若点P(m,y1),Q(4,y2)在抛物线上,且y1<y2,求m的取值范围.
2、如图,在平面直角坐标系中,四边形是平行四边形,,若、的长是关于的一元二次方程的两个根,且.
( http: / / www.21cnjy.com / )
(1)求、的长.
(2)若点为轴正半轴上的点,且,求经过、两点的直线解析式及经过点的反比例函数的解析式,并判断AOE与AOD是否相似.
(3)若点在平面直角坐标系内,则在直线上是否存在点,使以、、、为顶点且、为邻边的四边形为菱形?若存在,写出点的坐标,若不存在,请说明理由.
3、如图,抛物线与x轴交于A,B两点,与y轴交于C点,连接AC,已知B(﹣1,0),且抛物线经过点D(2,﹣2).
( http: / / www.21cnjy.com / )
(1)求抛物线的表达式;
(2)若点E是抛物线上第四象限内的一点,且,求点E的坐标;
(3)若点P是y轴上一点,以P,A,C三点为顶点的三角形是等腰三角形,求P点的坐标.
4、如图,一次函数yx﹣2的图象与坐标轴交于A,B两点,点C的坐标为(1,0),二次函数y=ax2+bx+c的图象经过A,B,C.
( http: / / www.21cnjy.com / )
(1)求抛物线的解析式;
(2)如图1,已知点D(﹣1,n)在抛物线上,作射线BD,Q为线段AB上一点,过点Q作QM⊥y轴于点M,作QN⊥BD于点N,过点Q作QPy轴交抛物线于点P,交BD于G,当QM与QN的积最大时,求点P的坐标;
(3)如图2,在(2)的条件下,连接AP,若E为抛物线上一点,且满足∠APE=2∠CAO,求点E的坐标.
5、有这样一类特殊边角特征的四边形,它们有“一组邻边相等且对角互补”,我们称之为“等对补四边形”.
( http: / / www.21cnjy.com / )
(1)如图1,四边形ABCD中,∠ ( http: / / www.21cnjy.com )BAD=∠BCD=90°,AD=AB,AE⊥CD于点E,若AE=4,则四边形ABCD的面积等于 .
(2)等对补四边形中,经过 ( http: / / www.21cnjy.com )两条相等邻边的公共顶点的一条对角线,必平分四边形的一个内角,即如图2,四边形ABCD中,AD=DC,∠A+∠C=180°,连接BD,求证:BD平分∠ABC.
(3)现准备在某地著名风景区开 ( http: / / www.21cnjy.com )发一片国家稀有动物核心保护区,保护区的规划图如图3所示,该地规划部门要求:四边形ABCD是一个“等对补四边形”,满足AD=DC,AB+AD=12,∠BAD=120°,因地势原因,要求3≤AD≤6,求该区域四边形ABCD面积的最大值.
-参考答案-
一、单选题
1、B
【解析】
【分析】
根据被开方数大于等于0,分母不等于0对各选项分别列式计算即可得解.
【详解】
解:A.中x≥1,此选项不符合题意;
B.中x>1,此选项符合题意;
C.中x≥,此选项不符合题意;
D.中x≥2,此选项不符合题意;
故答案选:B.
【点睛】
本题考查了函数自变量的范 ( http: / / www.21cnjy.com )围,一般从三个方面考虑:当函数表达式是整式时,自变量可取全体实数;当函数表达式是分式时,考虑分式的分母不能为0;当函数表达式是二次根式时,被开方数非负.
2、D
【解析】
【分析】
本题根据题意,判断一次函数和反比例函数的图象在哪个象限,即可判断的正负.
【详解】
反比例函数经过二、四象限,
,
一次函数经过二、三、四象限,
,
,
故选:D.
【点睛】
本题主要考查一次函数和反比例函数图象的性质,根据图象判断的正负是解题的关键.
3、B
【解析】
【分析】
根据二次函数的定义逐项判断即可.
【详解】
解:A.正方体集装箱的体积ym3,棱长xm,则y=x3,故不是二次函数;
B.高为14m的圆柱形储油罐的体积ym3,底面圆半径xm,则y=14πx2,故是二次函数;
C.妈妈买烤鸭花费86元,烤鸭的重量y斤,单价为x元/斤,则,故不是二次函数;
D.小莉驾车以108km/h的速度从南京出发到上海,行驶xh,距上海ykm,则y=南京与上海之间的距离-108x,故不是二次函数.21世纪教育网版权所有
故选:B.
【点睛】
本题考查二次函数的定义,解答本题的关键是明确题意,写出相应的函数解析式,利用二次函数的定义去判断.
4、A
【解析】
【分析】
由抛物线开口方向,对称轴位置,抛物 ( http: / / www.21cnjy.com )线与y轴交点位置可判断①,由抛物线对称轴和抛物线经过(﹣1,0)可得抛物线经过(3,0),从而可得b,c与a的关系,进而判断②,由x=﹣2时y<0可判断③,由x=1时y取最大值可判断④,由抛物线开口向下,对称轴为直线x=1可判断⑤,将ax2+bx+c﹣5=0化为只含系数a的方程,根据根与判别式的关系可判断⑥.21·cn·jy·com
【详解】
解:∵抛物线开口向下,
∴a<0,
∵抛物线对称轴为直线x=﹣=1,
∴b=﹣2a>0,
∵抛物线与y轴交点在x轴上方,
∴c>0,
∴abc<0,①正确.
∵抛物线经过点(﹣1,0),抛物线对称轴为直线x=1,
∴抛物线经过(3,0),
∴a﹣b+c=0,9a+3b+c=0,
∴10a+2b+2c=0,
∵b=﹣2a,
∴a=﹣,
∴﹣5b+2b+2c=﹣3b+2c=0,
∴b=c,
∴ c=b
∵抛物线与y轴交点位于(0,2)与(0,3)之间,
∴2<c<3,
∴2<b<3,
∴<b<2,②错误.
∵x=﹣2时,y<0,
∴4a﹣2b+c<0,③正确.
∵x=1时,y取最大值,
∴a+b+c≥am2+bm+c,
∴a+b≥am2+bm,④错误.
∵抛物线开口向下,2.5﹣1<1﹣(﹣2.5)
∴y1<y2,⑤错误.
∵b=c=﹣2a,
∴c=﹣3a,a=﹣c,
∵ 2<c<3
∴﹣1<﹣c<﹣
∴﹣1<a<﹣,
由ax2+bx+c﹣5=0可得ax2﹣2ax﹣3a﹣5=0,
∵﹣4<4a<﹣,1<4a +5<
∴Δ=(﹣2a)2﹣4a(﹣3a﹣5)=16a2+20a=4a(4a+5)<0,
∴方程ax2+bx+c﹣5=0无实数根,⑥错误.
故①③ 正确
故选:A.
【点睛】
本题考查二次函数图象与系数的关系,解题关键是掌握二次函数与方程及不等式的关系.
5、C
【解析】
【分析】
由反比例函数(k<0),可得 即函数图象分布在二,四象限,再结合点A(-3,y1),B(2,y2)是反比例函数(k<0)图象上的两点,判断的位置即可得到答案.
【详解】
解: 反比例函数(k<0),
即函数图象分布在二,四象限,
点A(-3,y1),B(2,y2)是反比例函数(k<0)图象上的两点,
故选C
【点睛】
本题考查的是反比例函数的图象与性质,掌握“当时,反比例函数的图象分布在第二,第四象限”是解本题的关键.2·1·c·n·j·y
6、A
【解析】
【分析】
根据反比例函数定义:形如的函数是反比例函数,即可得到答案.
【详解】
解:A、是反比例函数,故本选项符合题意;
B、是一次函数,故本选项不符合题意;
C、是二次函数,故本选项不符合题意;
D、是正比例函数,故本选项不符合题意;
故选A.
【点睛】
本题考查了反比例函数的定义,熟记正比例函数,反比例函数以及一次函数、二次函数的定义是解题的关键,是基础题,难度不大.【来源:21·世纪·教育·网】
7、B
【解析】
【分析】
先利用待定系数法求出抛物线解 ( http: / / www.21cnjy.com )析式,确定a的符号可判断①,利用函数值为0的两点横坐标为方程的解可判断②,利用图像解不等式确定自变量的取值范围可判断③,利用对称两的坐标可求对称轴可判断④.
【详解】
解:把(-2,2.5),(-1,0),(1,-2)代入抛物线解析式得:
,
解方程组得,
∴,
∴a=0.5>0,抛物线开口向上,故①正确;
∵(-1,0)和(3,0)在抛物线上,
∴当x=-1时,当x=3时,故②正确;
∵抛物线与x轴的交点坐标为(-1,0)和(3,0),
当时,函数图像在x轴下方,在两交点之间,x的取值范围是,故③正确;
∵抛物线的对称两点坐标为(-2,2.5),(4,2.5),
∴抛物线的对称轴为x=,故④不正确,
故正确的答案为①②③;
故选B.
( http: / / www.21cnjy.com / )
【点睛】
本题考查从表格获取信息与处理信息,待定系数 ( http: / / www.21cnjy.com )法求抛物线解析式确定抛物线性质,抛物线与x轴的交点的意义,利用图像与表格解不等式,确定自变量取值范围.
8、C
【解析】
【分析】
由题意得到抛物线的开口向上,对称轴﹣=,判断a,b与0的关系,即可判断①;根据抛物线对称轴方程可得a+b=0,即可判断②;根据抛物线y=ax2+bx+c经过点(2,0)以及c<0,得到4a+2b+3c<0,即可判断③;先根据a+b=0和4a+2b+c=0得c=﹣2a,再根据对称性可知:抛物线过(﹣1,0),即可判断④.【来源:21cnj*y.co*m】
【详解】
解:①∵抛物线开口向上,
∴a>0,
抛物线的对称轴为直线x=,即﹣=,,
∴b<0,故①正确;
②∵,
∴a+b=0,
故②不正确;
③∵抛物线y=ax2+bx+c(a,b,c为常数,a≠0)经过点(2,0),
∴4a+2b+c=0,
抛物线与y轴交点在负半轴,所以c<0,
∴4a+2b+3c<0,
故③正确;
④由对称得:抛物线与x轴另一交点为(﹣1,0),
∵,
∴c=﹣2a,
∴=﹣1,
∴无论a,b,c取何值,抛物线一定经过(,0),
故④正确;
本题正确的有:①③④,共3个.
故选:C.
【点睛】
本题考查了二次函数图象与系数的关系:对于 ( http: / / www.21cnjy.com )二次函数y=ax2+bx+c(a≠0),二次项系数a决定抛物线的开口方向和大小:当a>0时,抛物线向上开口;当a<0时,抛物线向下开口;一次项系数b和二次项系数a共同决定对称轴的位置:当a与b同号时(即ab>0),对称轴在y轴左;当a与b异号时(即ab<0),对称轴在y轴右;常数项c决定抛物线与y轴交点位置:抛物线与y轴交于(0,c).21教育网
9、D
【解析】
【分析】
直接把点(3,﹣4)代入反比例函数y=即可得出k的值.
【详解】
解:∵反比例函数y=的图象经过点(3,﹣4),
∴-4=,
解得k=-12.
故选D.
【点睛】
本题考查的是反比例函数图象上点的坐标特点,熟知反比例函数图象上各点的坐标一定适合此函数的解析式是解答此题的关键.www-2-1-cnjy-com
10、A
【解析】
【分析】
在图1中,由锐角三角函数求出AE长,以AB所在直线为x轴,CD所在直线为y轴,设抛物线的解析式为:y=ax2+3,进而求出a值,同理在图2中, A B 所在直线为x轴,C D 所在直线为y轴,设抛物线的解析式为:y=x2+b ,求出b ,即可得到C E ,由C D =C E +O E +O D 即可得解.
【详解】
解:如图1,
( http: / / www.21cnjy.com / )
在Rt△AOE中, AO=BO=3.6,∠AOE=60 ,
∴OE=OAsin60 =3.6×=1.8,AE= OAcos60 =3.6×=,
以AB所在直线为x轴,CD所在直线为y轴,
设抛物线的解析式为:y=ax2+3,
当x=时,y=a×()2+3=0,
∴a=,
如图2,
( http: / / www.21cnjy.com / )
在Rt△A O E 中, A O =B O =3.24,∠A O E =60 ,
∴O E =O A cos60 =3.24×=1.62,A E = O A sin60 =3.24×=,
以A B 所在直线为x轴,C D 所在直线为y轴,
设抛物线的解析式为:y=x2+b ,
当x=时,y=×()2+b =0,
∴b =2.43,即C E =2.43,
∴C D =C E +O E +O D =2.43+1.62+3.24=7.29cm.
故选:A
【点睛】
此题考查了待定系数法求二次函数解析式,锐角三角函数,建立适当的坐标系求二次函数解析式是解答此题的关键.
二、填空题
1、25
【解析】
【分析】
设DE=x,根据矩形的性质得到,PQ=MN=DE,证明△APN∽△ABC,得到,求出PN=10-x得到矩形的面积,根据二次函数的性质求解.
【详解】
解:设DE=x,
∵四边形PQMN是矩形,AD⊥BC,
∴,PQ=MN=DE,
∴△APN∽△ABC,
∴,
∴,
∴PN=10-x,
∴矩形PQMN面积=,
∴当x=5时,矩形PQMN面积有最大值,最大值为25cm2,
故答案为:25.
( http: / / www.21cnjy.com / ).
【点睛】
此题考查了矩形的性质,相似三角形的判定及性质,二次函数的最值,正确掌握相似三角形的判定及性质定理是解题的关键.
2、48
【解析】
【分析】
由菱形的性质和锐角三角函数可求点,将点坐标代入解析式可求的值.
【详解】
解:如图,过点作于点,
( http: / / www.21cnjy.com / )
菱形的边在轴上,点,
,
.
,
,
点坐标,
反比例函数经过点,
,
故答案为:48.
【点睛】
本题考查了反比例函数性质,反比例函数图象上点的坐标特征,菱形的性质,锐角三角函数,解题的关键是求出点坐标.
3、x≤﹣2或x≥1##x≥1或x≤﹣2
【解析】
【分析】
直接利用函数的交点坐标进而结合函数图象得出不等式ax2+bx+c≤px+q的解集.
【详解】
解:由图象可得点A左侧与点B右侧抛物线在直线下方,
∴x≤﹣2或x≥1时,ax2+bx+c≤px+q,
故答案为:x≤﹣2或x≥1.
【点睛】
此题主要考查了二次函数与不等式,正确数形结合分析是解题关键.
4、
【解析】
【分析】
根据函数图像求得正比例函数和反比例函数,进而根据题意求得时的自变量x的取值范围.
【详解】
解:根据题意设时,正比例函数为,时,反比例函数为,将点代入,得
,
当时,当时,
当时,当时,
根据函数图像可知,则体内抗体浓度y高于70微克/ml时,相应的自变量x的取值范围是
故答案为:
【点睛】
本题考查了正比例函数和反比例函数的应用,从函数图象获取信息是解题的关键.
5、①③##③①
【解析】
【分析】
①根据顶点的横坐标推出b=﹣2a,则ab=﹣2a2<0即可判断;
②当抛物线与x轴的交点都在x轴正半轴,则抛物线交y轴负半轴时,此时c<0先即可判断②;
③根据二次函数的性质,抛物线y=ax2+bx+c与直线y=m+1无交点,即可判断③;
③根据二次函数图象上点的坐标特征即可判断④.
【详解】
解:①∵抛物线y=ax2+bx+c(其中a,b,c是常数,m),
∴﹣=1,
∴b=﹣2a,
∴ab=﹣2a2<0,故①正确;
②由题意可知抛物线开口向下,对称轴为直线x=1,顶点坐标为(1,m),其中m>0
∴抛物线与x轴有两个交点,
当抛物线与x轴的交点在x轴正半轴,则抛物线交y轴负半轴时,故②错误;
③∵抛物线y=ax2+bx+c开口向下,函数有最大值m,
∴抛物线y=ax2+bx+c与直线y=m+1无交点,
∴关于x的一元二次方程ax2﹣bx+c=m+1无实数解,故③正确;
④抛物线y=ax2+bx+c开口向下,点P1(n,y1),P2(3﹣2n,y2)在抛物线上,
若n<1,则1﹣n<3﹣2n﹣1,
∴y1>y2.故④错误;
故答案为①③.
【点睛】
本题主要考查了二次函数图象与二次函数的系数的关系,解决本题的关键是二次函数的性质和一元二次方程与二次函数的关系.
三、解答题
1、 (1)y=-x2+4x﹣3;
(2)当a>0时0
【解析】
【分析】
(1)将点A代入解析式计算即可求出a,得到函数解析式;
(2)求出函数的对称轴,根 ( http: / / www.21cnjy.com )据对称性得到与点Q(4,y2)关于直线x=2对称的点的坐标为(0,y2),再分两种情况①当a>0时,②当a>0时,分别求出答案.21·世纪*教育网
(1)
解:将点A代入y=ax2﹣4ax﹣3,得a-4a-3=0,
解得a=-1,
∴该抛物线的解析式为y=-x2+4x﹣3;
(2)
解:∵抛物线的对称轴为直线,
∴与点Q(4,y2)关于直线x=2对称的点的坐标为(0,y2),
分两种情况:
①当a>0时,由y1<y2,得0
【点睛】
此题考查了求二次函数的解析式,二次函数的性质,分类讨论解决问题,正确理解二次函数的对称性是解题的关键.21*cnjy*com
2、 (1),
(2),,
(3)存在,,
【解析】
【分析】
(1)根据题意解一元二次方程即可;
(2)根据题意,设,根据求得的坐标,进而根据平行四边形的性质求得点的坐标,从而求得直线解析式;根据在反比例函数图象上求得反比例函数解析式;计算可得,根据夹角相等即可证明AOE与AOD相似;
(3)根据,又,可得平分,分二种情况考虑:①、是邻边;②、是邻边,进而根据菱形的性质求得点的坐标即可.
(1)
方程,分解因式得:,可得:,,
解得:,,
∵,
∴,;
(2)
根据题意,设,
则,
解得:,
∴,
∵四边形是平行四边形,
∴点的坐标是,
设经过、两点的直线的解析式为,
则,
解得:,
∴解析式为;
设反比例函数解析式为,把代入得:,
∴反比例函数解析式为;
在与中,
,,
∴,
又∵,
∴;
( http: / / www.21cnjy.com / )
(3)
根据计算的数据,,
∵,
∴平分,
分二种情况考虑:
①、是邻边,点在射线上时,,
∴点与重合,即;
②、是邻边,点在射线上时,应在直线上,且垂直平分,根据,,
∴此时点坐标为;
综上所述,满足条件的点有二个:;
( http: / / www.21cnjy.com / )
【点睛】
此题考查了解一元二次方程,相似三角形的性质与判定,待定系数法求函数解析式,综合性较强,求点要根据与是邻边的情况进行讨论,不要漏解.
3、 (1)
(2)E(,-1)
(3)P点的坐标(0,2)或(0,﹣2)或(0,﹣2﹣)或(0,)
【解析】
【分析】
(1)用待定系数法求解即可,将坐标代入表达式得解.
(2)欲求三角形得面积,通过A、B两点得坐 ( http: / / www.21cnjy.com )标,我们很轻松得得到AB得长度,同时E点纵坐标的绝对值就是新三角形的高,三角形的面积为2,通过面积公式,便可得解.因为抛物线的对称性,我们可以找到两个横坐标,又因为E点在第四象限,所以横坐标为正数,此题可解.
(3)如图2,设P(0,m),则PC =m+2,OA =3.根据勾股定理得到. ①当PA=CA时,则OP1= OC=2.②当PC = CA=时,可得即m+2=,解方程即可求解.③当PC= CA= 时,可得m=-2-, 于是得到结论.④当PC=PA时,点P在AC的垂直平分线上,根据相似三角形性质得到.
(1)
把B(﹣1,0),D(2,﹣2)
代入中,得
,
解得:.
∴ 抛物线的表达式为;
(2)
当y=0时,,
解得x1=﹣1,x2=3,
∴A(3,0),
∴AB=4,
如图1,过点E作x轴的垂线交x轴于点D,连接AE,BE.
设点点E(t,),其中0<t<3,
∴
∴,
解得,(舍去).
此时,
∴E(,-1).
( http: / / www.21cnjy.com / )
(3)
在中,当x=0时,y=﹣2,
∴C(0,﹣2)
∴OC=2,
如图2,设P(0,m),则PC=m+2,OA=3,AC=,
①当PA=CA时,则OP1=OC=2,
∴P1(0,2)
②当PC=CA=时,即m+2=,
∴m=﹣2,
∴P2(0,﹣2)
③当PC=CA=时,
,
m=﹣2﹣,
∴P3(0,﹣2﹣).
④当PC=PA时,点P在AC的垂直平分线上,
则△AOC∽△P4FC,
∴
∴
∴P4C=,
∴,
∴P4(0,),
综上所述,P点的坐标(0,2)或(0,﹣2)或(0,﹣2﹣)或(0,).
( http: / / www.21cnjy.com / )
【点睛】
本题考察了二次函数的综合题,涉 ( http: / / www.21cnjy.com )及待定系数法求函数解析式,等腰三角形的判定和性质,三角形的面积公式,利用相似三角形的比例建立表达式,正确地作出辅助线也是解题的关键.
4、 (1)y2;
(2)P(﹣2,﹣3);
(3)E(10,63)
【解析】
【分析】
(1)先求出点A、B的坐标,再利用待定系数法求解二次函数解析式即可;
(2)延长PQ交OB于H,延长NQ交OB于K,作DE⊥OB于E,先求得点D坐标,设Q(m,m﹣2),根据坐标与图形性质,先判断出△KNB和△KHQ为等腰直角三角形,再根据等腰直角三角形的性质表示出QN=NK﹣QK (m+6)(),进而有QM QN=﹣m ((m+2)2,然后根据二次函数的性质求解即可;21教育名师原创作品
(3)作PI⊥OA于I,在射线AI上截取IJ=IA,作∠APK=∠APJ交y轴于K,根据点P坐标可得AI=OC=1,PI=OA=2,进而可求得直线PJ的解析式是:y,与抛物线解析式联立,由得此时点E不存在,故作KT∥PJ交PA的延长线于T,利用角平分线的性质作AL⊥PJ于L,作AS⊥PK于S,求得AS=AL,PS=PL,进而在Rt△AKS中,利用勾股定理求解m值,进而求得点K的坐标,求出直线PK的解析式,与抛物线解析式联立方程组求解即可解答.
(1)
解:当y=0时,由x﹣2=0得:x=﹣4,
∴B(﹣4,0),
当x=0时,y=﹣2,
∴A(0,﹣2),
∴设抛物线的解析式是y=a(x+4)·(x﹣1),
∴a×4×(﹣1)=﹣2,
∴a,
∴y(x+4)·(x﹣1)2;
(2)
解:如图1,
( http: / / www.21cnjy.com / )
延长PQ交OB于H,延长NQ交OB于K,作DE⊥OB于E,
由题意得,n2=﹣3,
∴D(﹣1,﹣3),
∴DE=BE=3,
∴∠DBE=45°,
∴△KNB和△KHQ是等腰直角三角形,
设Q(m,m﹣2),
∴QM=﹣m,
HK=QH,
BH=m+4,
QK HK (),
BK=BH+HK,
∴NK BK (m+6),
∴QN=NK﹣QK
(m+6)()
,
∴QM QN=﹣m (
(m+2)2,
∴当m=﹣2时,QM QN最大,
∴当m=﹣2时,y(﹣2+4)×(﹣2﹣1)=﹣3,
∴P(﹣2,﹣3);
(3)
解:如图2,
( http: / / www.21cnjy.com / )
作PI⊥OA于I,在射线AI上截取IJ=IA,作∠APK=∠APJ交y轴于K,
∴PA=PJ,
∴∠APJ=2∠API,
∵P(﹣2,﹣3),A(0,﹣2),C(1,0),
∴AI=OC=1,PI=OA=2,
∴Rt△API≌Rt△CAO(SAS),
∴∠API=∠CAO,
∴∠APJ=2∠CAO,
∵P(﹣2,﹣3),J(0,﹣4),
∴直线PJ的解析式是:y,
由得,
∴x1=x2=﹣2,
∴此时点E不存在
作KT∥PJ交PA的延长线于T,
∴∠T=∠APJ=∠APK,,
即,
∴PK=KT,设KTm,AK=2m,
∴PKm,
作AL⊥PJ于L,作AS⊥PK于S,
∴AS=AL,PS=PL,
∵S△APJ,
∴ AL=2×2,
∴AS=AL,
∴PS=PL,
在Rt△AKS中,AK=2m,AS,SK=PK﹣PS,
∴()2+()2=(2m)2
∴m1=5,m2=1(舍去),
∴AK=2m=10,
∴K(0,8),
∴直线PK的解析式是:y,
由2得,
∴x1=10,x2=﹣2(舍去)
当x=10时,y63,
∴E(10,63).
【点睛】
本题考查二次函数的综合,涉及待 ( http: / / www.21cnjy.com )定系数法求二次函数解析式和一次函数的解析式、一次函数的图象与性质、等腰直角三角形的性质、解直角三角形、二次函数的最值、坐标与图形、全等三角形的判定与性质、勾股定理、解一元二次方程等知识,综合性强,难度困难,属于中考压轴题型,添加适当的辅助线,利用数形结合思想进行求解是解答的关键.21cnjy.com
5、 (1)9
(2)见解析
(3)
【解析】
【分析】
(1)过作,交的延长线于,求出四边形是矩形,根据矩形的性质得出,求出,根据得出,根据全等得出,,求出,求出,代入求出即可;2-1-c-n-j-y
(2)如图1中,连接,.证明,,,四点共圆,利用圆周角定理即可解决问题.
(3)如图3中,延长到,使得,连接,过点作于,根点作于,于.设.构建二次函数,利用二次函数的性质即可解决问题.
(1)
解:如图1,过作,交的延长线于,
( http: / / www.21cnjy.com / )
,
,
四边形是矩形,
,
,
,
在和中,
,
,
,,
四边形是矩形,
四边形是正方形,
,
.
故答案为:16;
(2)
解:证明:如图2中,连接.
( http: / / www.21cnjy.com / )
,
,,,四点共圆,
,
,
,
平分.
(3)
解:如图3中,延长到,使得,连接,过点作于,过点作于,于.设.
( http: / / www.21cnjy.com / )
,,
,
,
,
是等边三角形,
,
,
由(2)可知.平分,
,
,
,
,,
,,
,
,
,,
,
,
时,有最大值,最大值.
【点睛】
本题属于四边形综合题,考查了“邻等对补四边形 ( http: / / www.21cnjy.com )”的定义,解直角三角形,等边三角形的判定和性质,四点共圆,二次函数的应用等知识,解题的关键是理解题意,灵活运用所学知识解决问题,学会利用参数构建二次函数,利用二次函数的性质解决最值问题,属于中考压轴题.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
