第6章 平行四边形单元测试卷(含解析)

中小学教育资源及组卷应用平台
青岛版八年级数学下册第6章平行四边形单元测试
考试时间：90分钟；命题人：数学教研组
考生注意：
1、本卷分第I卷（选择题）和第Ⅱ卷（非选择题）两部分，满分100分，考试时间90分钟
2、答卷前，考生务必用0.5毫米黑色签字笔将自己的姓名、班级填写在试卷规定位置上
3、答案必须写在试卷各个题目指定区域内相应的 ( http: / / www.21cnjy.com )位置，如需改动，先划掉原来的答案，然后再写上新的答案；不准使用涂改液、胶带纸、修正带，不按以上要求作答的答案无效。www.21-cn-jy.com
第I卷（选择题 30分）
一、单选题（10小题，每小题3分，共计30分）
1、菱形ABCD的边长为5，一条对角线长为6，则菱形面积为（　　）
A．20 B．24 C．30 D．48
2、如图，E、F分别是正方形ABCD的边CD、BC上的点，且，AF、BE相交于点G，下列结论中正确的是（ ）2·1·c·n·j·y
①；②；③；④．
( http: / / www.21cnjy.com / )
A．①②③ B．①②④ C．①③④ D．②③④
3、小明想判断家里的门框是否为矩形，他应该（ ）
A．测量三个角是否都是直角 B．测量对角线是否互相平分
C．测量两组对边是否分别相等 D．测量一组对角是否是直角
4、下列命题中是真命题的是（ ）．
A．有一组邻边相等的平行四边形是菱形 B．对角线互相垂直且相等的四边形是菱形
C．对角线相等的四边形是矩形 D．有一个角为直角的四边形是矩形
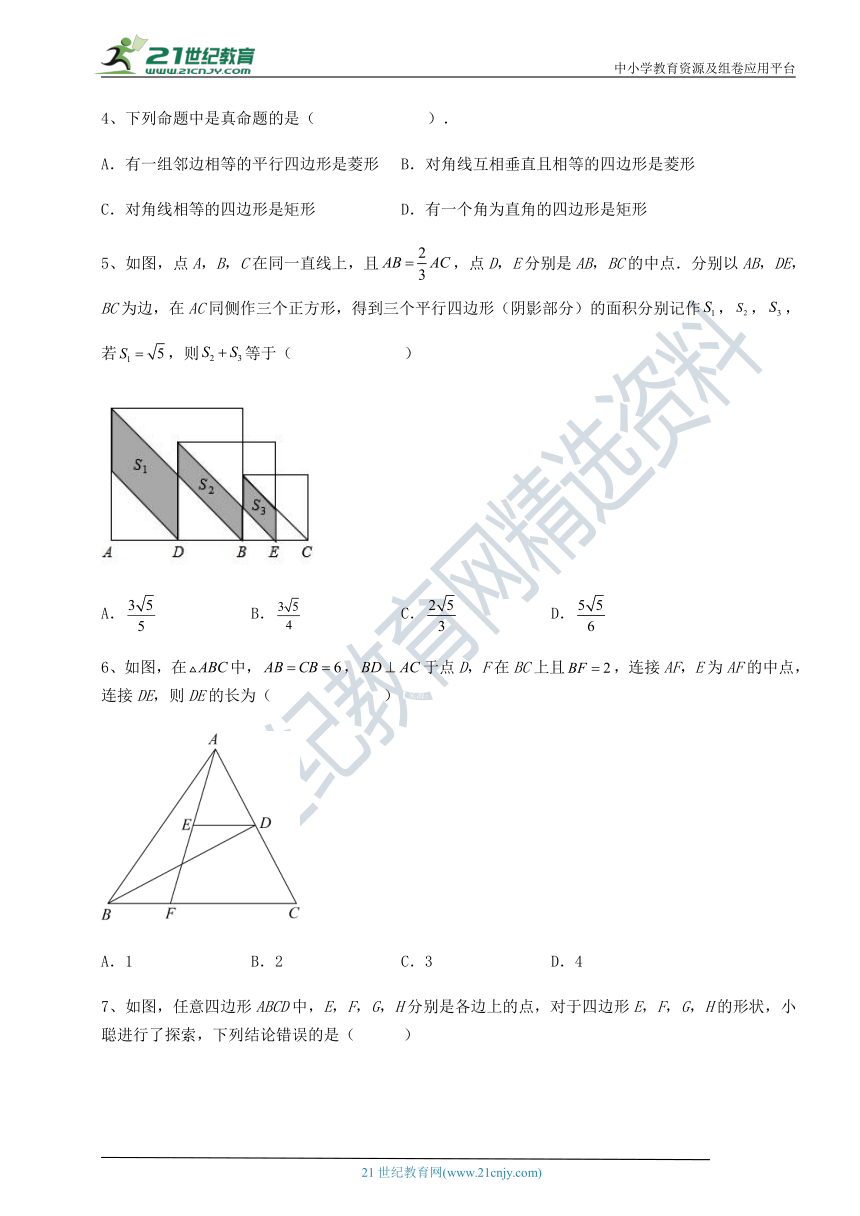
5、如图，点A，B，C在同一直线上，且，点D，E分别是AB，BC的中点．分别以AB，DE，BC为边，在AC同侧作三个正方形，得到三个平行四边形（阴影部分）的面积分别记作，，，若，则等于（ ）【来源：21·世纪·教育·网】
( http: / / www.21cnjy.com / )
A． B． C． D．
6、如图，在中，，于点D，F在BC上且，连接AF，E为AF的中点，连接DE，则DE的长为（ ）【来源：21cnj*y.co*m】
( http: / / www.21cnjy.com / )
A．1 B．2 C．3 D．4
7、如图，任意四边形ABCD中，E，F，G，H分别是各边上的点，对于四边形E，F，G，H的形状，小聪进行了探索，下列结论错误的是（　　　）21教育名师原创作品
( http: / / www.21cnjy.com / )
A．E，F，G，H是各边中点．且AC=BD时，四边形EFGH是菱形
B．E，F，G，H是各边中点．且AC⊥BD时，四边形EFGH是矩形
C．E，F，G，H不是各边中点．四边形EFGH可以是平行四边形
D．E，F，G，H不是各边中点．四边形EFGH不可能是菱形
8、下面性质中，平行四边形不一定具备的是（　　）
A．对角互补 B．邻角互补
C．对角相等 D．对角线互相平分
9、已知点D、E、F分别为各边的中点，若的周长为24cm，则的周长为（ ）．
A．6cm B．12cm C．24cm D．48cm
10、下列命题错误的是（ ）
A．两组对边分别平行的四边形是平行四边形
B．两组对边分别相等的四边形是平行四边形
C．一组对边平行，另一组对边相等的四边形是平行四边形
D．对角线互相平分的四边形是平行四边形
第Ⅱ卷（非选择题 70分）
二、填空题（5小题，每小题4分，共计20分）
1、如图，矩形的两条对角线相交于点，已知，，则矩形对角线的长为_______．
( http: / / www.21cnjy.com / )
2、平行四边形的判定方法：
（1）两组对边分别______的四边形是平行四边形
（2）两组对边分别______的四边形是平行四边形
（3）两组对角分别______的四边形是平行四边形
（4）对角线______的四边形是平行四边形
（5）一组对边______的四边形是平行四边形
3、（1）平行四边形的对边________．
几何语言：因为四边形ABCD是平行四边形，所以AB＝________，AD＝________．　
( http: / / www.21cnjy.com / )
（2）平行四边形的对角________．
几何语言：因为四边形ABCD是平行四边形，所以∠A＝________，∠B＝________．
4、将两个直角三角板如图放置，其中 ( http: / / www.21cnjy.com )AB＝AC，∠BAC＝∠ECD＝90°，∠D＝60°．如果点A是DE的中点，CE与AB交于点F，则∠BFC的度数为 _____°．【出处：21教育名师】
( http: / / www.21cnjy.com / )
5、如图，在平行四边形ABCD中，AB ( http: / / www.21cnjy.com )＝5，BC＝8．E是边BC的中点，F是平行四边形ABCD内一点，且∠BFC＝90°．连接AF并延长，交CD于点G．若EF∥AB，则DG的长为 _____．
( http: / / www.21cnjy.com / )
三、解答题（5小题，每小题10分，共计50分）
1、在矩形ABCD的CD边上取一点E，将沿BE翻折，得到．
( http: / / www.21cnjy.com / )
(1)如图1，点F恰好在AD上，若，求出AB：BC的值．
(2)如图2，E从C到D的运动过程中．
①若，，的角平分线交EF的延长线于点M，求M到AD的距离：
②在①的条件下，E从C到D的过程中，直接写出M运动的路径长．
2、已知：如图，菱形ABCD中，∠B=60°，点E，F在边BC，CD上，且∠EAF=60°；求证：AE=AF．
( http: / / www.21cnjy.com / )
3、如图，正方形ABCD和正方形CEFG，点G在CD上，AB＝5，CE＝2，T为AF的中点，求CT的长．
( http: / / www.21cnjy.com / )
4、已知如图，四边形ABCD是平行四边形．
( http: / / www.21cnjy.com / )
（1）尺规作图：作∠ABC的角平分线交CD的延长线于E，交AD于F（不写作法和证明，但要保留作图痕迹）．
（2）请在（1）的情况下，求证：DE＝DF．
5、如图1，在△ABC中，∠ACB＝90°， ( http: / / www.21cnjy.com )AC＝4cm，BC＝3cm．如果点P由点B出发沿BA方向向点A匀速运动，同时点Q由点A出发沿AC方向向点C匀速运动，它们的速度均为1cm/s．连接PQ，设运动时间为t（s）（0＜t＜4），解答下列问题：
( http: / / www.21cnjy.com / )
(1)填空：用含t的代数式表示AQ＝　 　，AP＝　 　．
(2)如图2，连接PC，将△PQC沿QC翻折，得到四边形PQP′C，当四边形PQP′C为菱形时，求t的值；
(3)当t为何值时，△APQ是等腰三角形？
-参考答案-
一、单选题
1、B
【解析】
【分析】
根据菱形的性质利用勾股定理求得另一条对角线，再根据菱形的面积等于两对角线乘积的一半求得菱形的面积．
【详解】
解：如图，当BD＝6时，
( http: / / www.21cnjy.com / )
∵四边形ABCD是菱形，
∴AC⊥BD，AO＝CO，BO＝DO＝3，
∵AB＝5，
∴AO＝=4，
∴AC＝8，
∴菱形的面积是：6×8÷2＝24，
故选：C．
【点睛】
本题主要考查菱形的面积公式，以及菱形的性质和勾股定理，关键是掌握菱形的面积等于两条对角线的积的一半．
2、B
【解析】
【分析】
根据正方形的性质及全等三角形的判定定理和性质、垂直的判定依次进行判断即可得．
【详解】
解：∵四边形ABCD是正方形，
∴，，
在与中，
，
∴，
∴，①正确；
∵，
，
∴，
∴，
∴，②正确；
∵GF与BG的数量关系不清楚，
∴无法得AG与GE的数量关系，③错误；
∵，
∴，
∴，
即，④正确；
综上可得：①②④正确，
故选：B．
【点睛】
题目主要考查全等三角形的判定和性质，正方形的性质，垂直的判定等，理解题意，综合运用全等三角形全等的判定和性质是解题关键．
3、A
【解析】
【分析】
根据矩形的判定方法解题．
【详解】
解：A、三个角都是直角的四边形是矩形，
选项A符合题意；
B、对角线互相平分的四边形是平行四边形，
选项B不符合题意，
C、两组对边分别相等的四边形是平行四边形，
选项C不符合题意；
D、一组对角是直角的四边形不是矩形，
选项D不符合题意；
故选：A．
【点睛】
本题考查矩形的判定方法，是重要考点，掌握相关知识是解题关键．
4、A
【解析】
【分析】
根据平行线四边形的性质得到对边相等，加上 ( http: / / www.21cnjy.com )一组邻边相等，可得到四边都相等，根据菱形的定义对A、B进行判断；根据矩形的判定方法对C、D进行判断．
【详解】
解：A、平行四边形的对边相等，若有一组邻边相等，则四边都相等，所以该选项正确；
B、对角线互相平分且垂直的四边形是菱形，所以该选项不正确；
C、对角线互相平分且相等的四边形为矩形，所以该选项不正确；
D、有三个角是直角的四边形是矩形，所以该选项不正确．
故选：A．
【点睛】
本题考查了命题与定理：判断事情的语句叫命题 ( http: / / www.21cnjy.com )；正确的命题叫真命题；经过证明其正确性的命题称为定理．也考查了平行四边形、矩形和菱形的判定与性质．
5、B
【解析】
【分析】
设BE＝x，根据正方形的性质、平行四边形的面积公式分别表示出S1，S2，S3，根据题意计算即可．
【详解】
∵，
∴AB＝2BC，
又∵点D，E分别是AB，BC的中点，
∴设BE＝x，则EC＝x，AD＝BD＝2x，
( http: / / www.21cnjy.com / )
∵四边形ABGF是正方形，
∴∠ABF＝45°，
∴△BDH是等腰直角三角形，
∴BD＝DH＝2x，
∴S1＝DH AD＝，即2x 2x＝，
∴x2＝，
∵BD＝2x，BE＝x，
∴S2＝MH BD＝（3x 2x） 2x＝2x2，
S3＝EN BE＝x x＝x2，
∴S2＋S3＝2x2＋x2＝3x2＝，
故选：B．
【点睛】
本题考查的是正方形的性质、平行四边形的性质，掌握正方形的四条边相等、四个角都是90°是解题的关键．
6、B
【解析】
【分析】
先求出，再根据等腰三角形的三线合一可得点是的中点，然后根据三角形中位线定理即可得．
【详解】
解：，
，
，
（等腰三角形的三线合一），
即点是的中点，
为的中点，
是的中位线，
，
故选：B．
【点睛】
本题考查了等腰三角形的三线合一、三角形中位线定理，熟练掌握等腰三角形的三线合一是解题关键．
7、D
【解析】
【分析】
当为各边中点，，，四边形是平行四边形；A中AC=BD，则，平行四边形为菱形，进而可判断正误；B中AC⊥BD，则，平行四边形为矩形，进而可判断正误；E，F，G，H不是各边中点，C中若四点位置满足，则可知四边形EFGH可以是平行四边形，进而可判断正误；D中若四点位置满足，则可知四边形EFGH可以是菱形，进而可判断正误．【版权所有：21教育】
【详解】
解：如图，连接当为各边中点时，可知分别为的中位线
( http: / / www.21cnjy.com / )
∴
∴四边形是平行四边形
A中AC=BD，则，平行四边形为菱形；正确，不符合题意；
B中AC⊥BD，则，平行四边形为矩形；正确，不符合题意；
C中E，F，G，H不是各边中点，若四点位置满足，则可知四边形EFGH可以是平行四边形；正确，不符合题意；21·世纪*教育网
D中若四点位置满足，则可知四边形EFGH可以是菱形；错误，符合题意；
故选D．
【点睛】
本题考查了平行四边形、菱形、矩形的判定，中位线等知识．解题的关键在于熟练掌握特殊平行四边形的判定．
8、A
【解析】
【分析】
直接利用平行四边形的性质：对角相等、对角线互相平分、对边平行且相等，进而分析得出即可．
【详解】
解：A、平行四边形对角不一定互补，故符合题意；
B、平行四边形邻角互补正确，故不符合题意；
C、平行四边形对角相等正确，故不符合题意．
D、平行四边形的对角线互相平分正确，故不符合题意；
故选A．
【点睛】
此题主要考查了平行四边形的性质，熟练掌握相关性质是解题关键．
9、B
【解析】
【分析】
根据三角形中位线的判定和性质解题即可．
【详解】
解：∵D、E、F分别为三边的中点，
( http: / / www.21cnjy.com / )
∴DE、DF、EF都是的中位线，
∴，，，
故的周长．
故选：B．
【点睛】
本题考查三角形中位线的判定和性质．掌握三角形中位线平行于第三边且等于第三边的一半是解题关键．
10、C
【解析】
【分析】
根据平行四边形的判定逐项分析即可得．
【详解】
解：A、两组对边分别平行的四边形是平行四边形，正确，则此项不符合题意；
B、两组对边分别相等的四边形是平行四边形，正确，则此项不符合题意；
C、一组对边平行，另一组对边相等的四边形可能是平行四边形，也可能是等腰梯形，故原命题错误，此项符合题意；21世纪教育网版权所有
D、对角线互相平分的四边形是平行四边形，正确，则此项不符合题意，
故选：C．
【点睛】
本题考查了平行四边形的判定，熟记平行四边形的判定是解题关键．
二、填空题
1、5
【解析】
【分析】
由矩形的性质可证△AOB为等边三角形，可求BO=AB的长，即可求BD的长．
【详解】
解：∵四边形ABCD是矩形，
∴AO=CO=BO=DO，
∵∠AOD=120°，
∴∠AOB=60°，且AO=BO，
∴△ABO为等边三角形，
∴AO=BO=AB=2.5，
∴BD=5，
故答案为：5．
【点睛】
本题考查矩形的性质，熟练掌握矩形的性质是本题的关键，①矩形的对边平行且相等；②矩形的四个角都是直角；③矩形的对角线相等且互相平分．21·cn·jy·com
2、 平行 相等 相等 互相平分 平行且相等
【解析】
略
3、 相等 CD BC 相等 ∠C ∠D
【解析】
略
4、120
【解析】
【分析】
先根据直角三角形斜边上的中线等于斜边的一半得出AC=AD=AE=DE，由∠D=60°，得到△ACD是等边三角形，那么∠ACD=60°，∠ACF=30°，再由三角形的外角性质可求出∠BFC的度数．
【详解】
解：∵∠DCE=90°，点A是DE的中点，
∴AC=AD=AE=DE，
∵∠D=60°，
∴△ACD是等边三角形，
∴∠ACD=60°，
∴∠ACF=∠DCE-∠ACD=30°，
∵∠FAC=90°，
∴∠BFC=∠FAC+∠ACF=90°+30°=120°
故答案为：120
【点睛】
本题主要考查了直角三角形的性质，等边三角形的判定与性质，三角形外角和定理等知识，求出∠ACF =30°是解题的关键．
5、2
【解析】
【分析】
延长BF交CD的延长线于H， ( http: / / www.21cnjy.com )可证EF是△BCH的中位线，由中垂线的性质可得BC＝CH＝8，可求DH＝3，由“ASA”可证△ABF≌△GFH，可得AB＝GH＝5，可求解．
【详解】
解：如图，延长BF交CD的延长线于H，
( http: / / www.21cnjy.com / )
∵四边形ABCD是平行四边形，
∴AB＝CD＝5，AB∥CD，
∴∠H＝∠ABF，
∵EF∥AB，
∴EF∥CD，
∵E是边BC的中点，
∴EF是△BCH的中位线，
∴BF＝FH，
∵∠BFC＝90°，
∴CF⊥BF，
∴CF是BH的中垂线，
∴BC＝CH＝8，
∴DH＝CH﹣CD＝3，
在△ABF和△GHF中，
，
∴△ABF≌△GFH（ASA），
∴AB＝GH＝5，
∴DG＝GH﹣DH＝2，
故答案为：2．
【点睛】
本题主要考查了平行四边形的性质，全等三角形的判定和性质，三角形中位线定理等知识，灵活运用这些性质进行推理是本题的关键．www-2-1-cnjy-com
三、解答题
1、 (1)
(2)①3，②
【解析】
【分析】
（1）①设DF=m，解直角三角形求出AB，AD（用m表示即可）；
（2）①如图，过点M作M ( http: / / www.21cnjy.com )K⊥AD于K，MH⊥BA交BA的延长线于H，交CD的延长线于G．证明△BMH≌△BMF（AAS），推出BH=BF=8，可得结论．21*cnjy*com
②如图3-2中，当点E与D重合时，求出MG的长，可得结论．
(1)
如图，设DF=m．
( http: / / www.21cnjy.com / )
∵四边形ABCD是矩形，
∴∠A=∠D=∠C=90°，AB=CD，AD=BC，
由翻折的性质可知，∠BEF=∠BEC=75°，∠C=∠BFE=90°，EF=EC，
∴∠FED=180°-75°-75°=30°，
∴EF=EC=2DF=2m，DE=DF=m，
∴∠AEFD=60°，∠AFB=30°，AB=CD=2m+m，
∵AF=AB=2m+3m，
∴BC=AD=2m+4m，
∴．
(2)
①如图，过点M作MK⊥AD于K，MH⊥BA交BA的延长线于H，交CD的延长线于G．
( http: / / www.21cnjy.com / )
∵四边形ABCD是矩形，
∴∠C=∠BAD=∠ABD=∠ADC=90°，AB=CD=5，AD=BC=8，
∵MH⊥AB，MK⊥AD，
∴∠H=∠HAK=∠AKM=90°，
∴四边形AKMH是矩形，
∴AH=MK，
∵BM平分∠ABF，
∴∠MBH=∠MBF，
∵∠H=∠AFM=90°，BM=BM，
∴△BMH≌△BMF（AAS），
∴BH=BF，
∵BF=BC=8，
∴BH=BC=8，
∴MK=AH=BH-AB=8-5=3，
∴M到AD的距离为3．
②如图，当点E与D重合时，
( http: / / www.21cnjy.com / )
∵△BMH≌△BMF，
∴MH=MF，
设MH=MF=m，
∵四边形AHGD是矩形，
∴AH=DG=3，GH=AD=8，∠G=90°，
∵CD=DF=5，GM=GH-HM=8-m，
在Rt△DGM中，则有（8-m）2+32=（5+m）2，
解得m=，
∴GM=8-=，
观察图象可知，当E从C到D的过程中，点M运动的路径是线段MG，
∴点M的运动的路径的长为．
【点睛】
本题考查了矩形的性质，全等三角形的判定 ( http: / / www.21cnjy.com )与性质，直角三角形的性质，折叠的性质，角平分线的性质，勾股定理等知识，判断出BH=BF=BC是解题的关键．21*cnjy*com
2、见解析
【解析】
【分析】
连接AC，如图，根据菱形的 ( http: / / www.21cnjy.com )性质得AB=BC，而∠B=60°，则可判定△ABC为等边三角形，得到∠2=60°，∠1+∠4=60°，AC=AB，易得∠ACF=60°，∠1=∠3，然后利用“ASA”可证明△AEB≌△AFC，于是得到AE=AF．
【详解】
解：证明：连接AC，如图，
( http: / / www.21cnjy.com / )
∵四边形ABCD为菱形，
∴AB=BC，
∵∠B=60°，
∴△ABC为等边三角形，
∴∠2=60°，∠1+∠4=60°，AC=AB，
∴∠ACF=60°，
∵∠EAF=60°，即∠3+∠4=60°，
∴∠1=∠3，
在△AEB和△AFC中，
，
∴△AEB≌△AFC，
∴AE=AF．
【点睛】
本题考查了菱形的性质：菱形具有 ( http: / / www.21cnjy.com )平行四边形的一切性质；菱形的四条边都相等；菱形的两条对角线互相垂直，并且每一条对角线平分一组对角；菱形是轴对称图形，它有2条对称轴，分别是两条对角线所在直线．也考查了全等三角形的判定与性质．21教育网
3、
【解析】
【分析】
连接AC，CF，如图，根据正方形的性质得到AC=，AB=5，CF=CE=2，∠ACD=45°，∠GCF=45°，则利用勾股定理得到AF=，然后根据直角三角形斜边上的中线性质得到CT的长．
【详解】
解：连接AC、CF，如图，
( http: / / www.21cnjy.com / )
∵四边形ABCD和四边形CEFG都是正方形，
∴AC=AB=5，CF=CE=2，∠ACD=45°，∠GCF=45°，
∴∠ACF=45°+45°=90°，
在Rt△ACF中，
∵T为AF的中点，
∴，
∴CT的长为．
【点睛】
本题考查了正方形的性质：正方形的四 ( http: / / www.21cnjy.com )条边都相等，四个角都是直角；正方形的两条对角线相等，互相垂直平分，并且每条对角线平分一组对角；正方形具有四边形、平行四边形、矩形、菱形的一切性质，也考查了直角三角形斜边上的中线性质．2-1-c-n-j-y
4、（1）图见解析；（2）证明见解析．
【解析】
【分析】
（1）根据角平分线的尺规作图即可得；
（2）先根据平行四边形的性质可得，再根据平行线的性质可得，然后根据角平分线的定义可得，从而可得，最后根据等腰三角形的判定即可得证．
【详解】
解：（1）尺规作图如下：
( http: / / www.21cnjy.com / )
（2）四边形是平行四边形，
，
，
平分，
，
，
．
【点睛】
本题考查了角平分线的尺规作图、平行四边形的性质等知识点，熟练掌握平行四边形的性质是解题关键．
5、 (1)t；5-t
(2)
(3)当
【解析】
【分析】
（1）根据勾股定理求得，进而求得结果；
（2）当时，四边形是菱形，作于，根据，表示出，根据列出方程求得结果；
（3）分为，，三种情形，当可得：，当时，作于，，由，可得，进而得到方程求得结果，当时，作于，可得，根据，表示出，进而得出方程求得结果．
(1)
解：（1）在中，
，
，
故答案是：，；
(2)
（2）如图1，
( http: / / www.21cnjy.com / )
作于，
四边形是菱形，
，
，
，
，
，
，
，
；
(3)
（3）当时，
，
，
如图2，
( http: / / www.21cnjy.com / )
当时，
作于，
，
，
．
，
，
如图3，
( http: / / www.21cnjy.com / )
当时，
作于，
，
，
，
，
，
综上所述，或或．
【点睛】
本题考查了菱形的判定和性质，等腰三角形的判定和性质，解直角三角形等知识，解决问题的关键是正确分类并列方程．21cnjy.com
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 （共 2 页）
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)