第6章 频率与概率章节练习试卷(含解析)
图片预览




文档简介
中小学教育资源及组卷应用平台
九年级数学下册第6章事件的概率章节练习
考试时间:90分钟;命题人:数学教研组
考生注意:
1、本卷分第I卷(选择题)和第Ⅱ卷(非选择题)两部分,满分100分,考试时间90分钟
2、答卷前,考生务必用0.5毫米黑色签字笔将自己的姓名、班级填写在试卷规定位置上
3、答案必须写在试卷各个题目指定 ( http: / / www.21cnjy.com )区域内相应的位置,如需改动,先划掉原来的答案,然后再写上新的答案;不准使用涂改液、胶带纸、修正带,不按以上要求作答的答案无效。21世纪教育网版权所有
第I卷(选择题 30分)
一、单选题(10小题,每小题3分,共计30分)
1、下列说法中,正确的是( )
A.可能性很大的事情是必然发生的
B.可能性很小的事情是不可能发生的
C.如果圆的半径为,则该圆的周长为是必然的
D.冬季里下雪是一定发生的
2、在下图的各事件中,是随机事件的有( )
A.1个 B.2个 C.3个 D.4个
3、在一个不透明的盒子中装 ( http: / / www.21cnjy.com )有n个小球,它们除了颜色不同外,其余都相同,其中有4个白球.每次试验前,将盒子中的小球摇匀,随机摸出一个球记下颜色后再放回盒中.大量重复上述试验后发现,摸到白球的频率稳定于0.4,则n的值为( )【来源:21·世纪·教育·网】
A.6 B.10 C.14 D.18
4、在一个不透明的盒子中装有30个白、黄两种 ( http: / / www.21cnjy.com )颜色的乒乓球,这些乒乓球除颜色外都相同. 班长进行了多次的摸球试验,发现摸到黄色乒乓球的频率稳定在0.3左右,则盒子中的白色乒乓球的个数可能是( )2-1-c-n-j-y
A.21个 B.15个 C.12个 D.9个
5、下列事件是必然事件的是( )
A.某种彩票中奖率为1%,则买100张这种彩票必然中奖
B.今晚努力学习,明天考试必然考出好成绩
C.从装有2个红球、3个白球的袋中随机摸出4个球,则一定会摸出红球
D.抛掷一枚普通的骰子所得的点数一定小于6
6、如图是一个游戏转盘.自由转动转盘,当转盘停止转动后,指针落在数字1,2,3,4所示区域内可能性最大的是( )【来源:21cnj*y.co*m】
( http: / / www.21cnjy.com / )
A.1号 B.2号 C.3号 D.4号
7、某火车站的显示屏每间隔 ( http: / / www.21cnjy.com )4分钟显示一次火车班次的信息,显示时间持续1分钟,某人到达该车站时,显示屏正好显示火车班次信息的概率是( )
A. B. C. D.
8、有4张背面相同的卡片,正面分别印有 ( http: / / www.21cnjy.com )平行四边形、矩形、菱形、正方形,现将4张卡片正面朝下一字摆开,从中随机抽取两张,抽到的两张卡片上都恰好印的既是中心对称又是轴对称的图形的概率为( )
A.1 B. C. D.
9、一个不透明的盒子中有100个红色小球,10个白色小球,1个黄色小球,现从中随机取出一个球,下列事件是不可能事件的是( )
A.取出的是红色小球 B.取出的是白色小球
C.取出的是黄色小球 D.取出的是黑色小球
10、下列说法:①不可能事件发生的概率为0;②随机事件发生的概率为;③事件发生的概率与实验次数无关;④“画一个矩形,其对角线互相垂直”是必然事件.其中正确的是( )
A.①② B.②③ C.①③ D.①④
第Ⅱ卷(非选择题 70分)
二、填空题(5小题,每小题4分,共计20分)
1、一个布袋里装有2个只有颜 ( http: / / www.21cnjy.com )色不同的球,其中1个红球,1个白球,从布袋里摸出1个球,记下颜色后放回,搅匀,再摸出1个球,则两次摸到的球恰好颜色不同的概率是______.
2、杨老师对自己所教班级( ( http: / / www.21cnjy.com )共50名学生)的一次数学测验成绩进行统计.结果是:成绩在80.5~90.5(分)这一组的频数是15,那么本班成绩在80.5~90.5分之间的频率是__________.
3、把50个数据分成五组,第一、二、三、四、五组的数据个数分别是8,15,x,12,5,则第三组的频率为______.
4、如图,⊙O与正方形ABC ( http: / / www.21cnjy.com )D各边相切,若随机向正方形内投一粒米(将米粒看成一个点),则米粒落在阴影部分的概率是__________________.
( http: / / www.21cnjy.com / )
5、现将背面完全相同,正面分别标 ( http: / / www.21cnjy.com )有数﹣1,1,2,3的四张卡片洗匀后,背面朝上,从中任取一张,将该卡片上的数标记为m,再从剩下的三张卡片中任取一张,将该卡片上的数记为n,则P(m,n)在第四象限的概率为_____.
三、解答题(5小题,每小题10分,共计50分)
1、在如今手机的功能中,都可以利用手势密码进行锁屏和解锁.其中最常见的就是利用的正方形点阵设置密码,我们将其称为“9点码”.通常,在设置“9点码”时,只能连接相邻的两点(如图,不妨将9个点依次对应数字1到9;例如图中路线Ⅰ,Ⅱ等是可行的,路线Ⅲ,Ⅳ是不可行的),不能走重复的路线,从而形成相应的密码线段,线段越多,密码越复杂.已知小明设置的“9点码”从右上角的点“3”出发,且用了3个数字.
( http: / / www.21cnjy.com / )
(1)已知横向和纵向的相邻两点距离为1, ( http: / / www.21cnjy.com )且小明设置的“9点码”的密码线段恰好构成了一个等腰三角形,则该等腰三角形的面积所有可能的值为______;
(2)用概率知识并结合树状图回答 ( http: / / www.21cnjy.com ):若小明设置的“9点码”用了3个数字,对于一个不知道该密码的人,通过画树状图,求其一次尝试能将小明手机解锁的概率.
2、某市准备举行初中生“党史知识竞赛” ( http: / / www.21cnjy.com ),学校通过初赛选出了2位男生A、B和2位女生C、D共4位选手,准备从4人中任选2人代表学校参加比赛.求所选代表都是女生的概率.
3、中国古代有着辉煌的数学成就,《周髀算经》,《九章算术》,《海岛算经》,《孙子算经》等是了解我国古代数学的重要文献.
(1)小华想从这4部数学名著中随机选择1部阅读,求他选中《孙子算经》的概率;
(2)某中学拟从这4部数学 ( http: / / www.21cnjy.com )名著中选择2部作为“数学文化”校本课程学习内容,用列表法或树状图法求出选中的2部名著中,其中1部是《周髀算经》的概率.
4、为迎接中国共产党建党100周年, ( http: / / www.21cnjy.com )某校组织七、八年级学生开展了党史知识竞赛.现从两个年级各随机抽取15名学生的竞赛成绩(百分制)进行分析,过程如下:21*cnjy*com
【收集数据】
七年级:89,74,85,80,81,92,58,99,80,82,90,76,80,85,64.
八年级:91,72,92,80,83,92,88,82,85,83,76,83,82,80,46.
【整理数据】
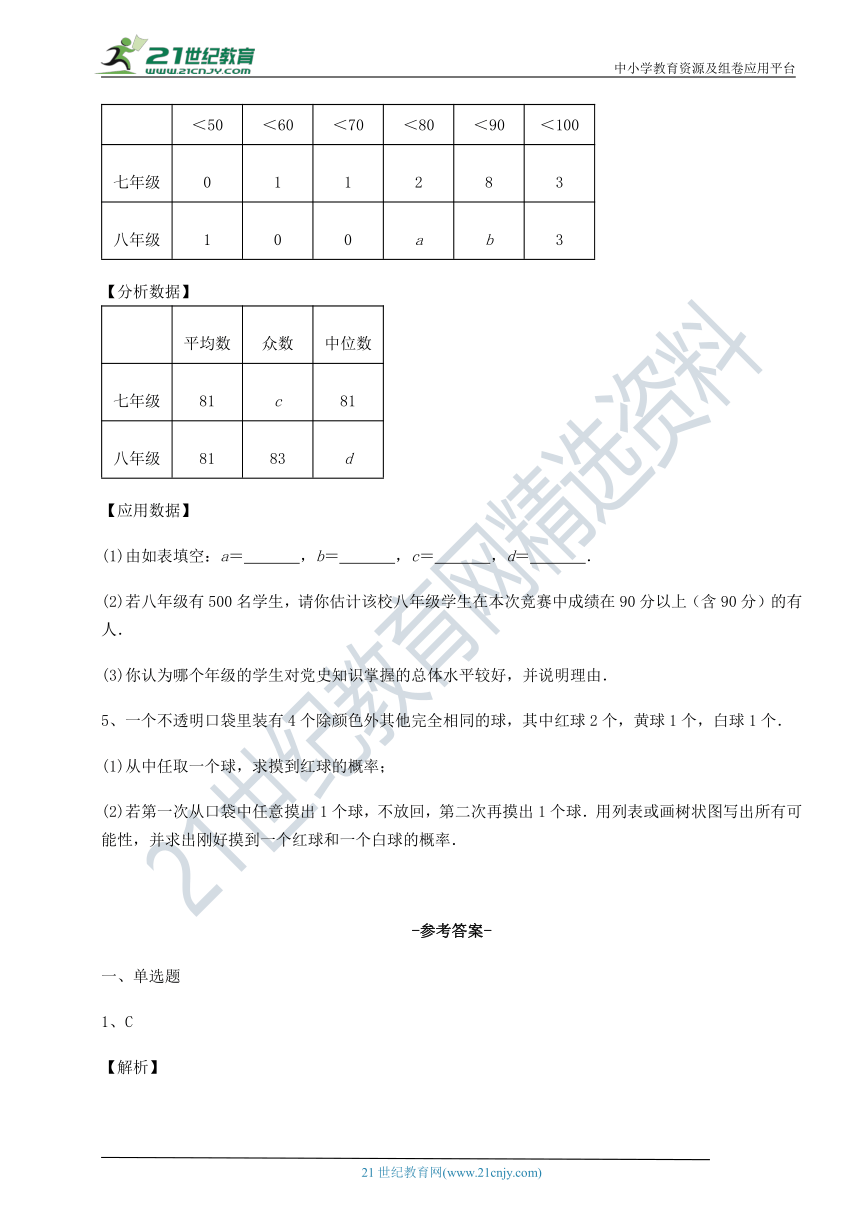
40≤x<50 50≤x<60 60≤x<70 70≤x<80 80≤x<90 90≤x<100
七年级 0 1 1 2 8 3
八年级 1 0 0 a b 3
【分析数据】
平均数 众数 中位数
七年级 81 c 81
八年级 81 83 d
【应用数据】
(1)由如表填空:a= ,b= ,c= ,d= .
(2)若八年级有500名学生,请你估计该校八年级学生在本次竞赛中成绩在90分以上(含90分)的有 人.www.21-cn-jy.com
(3)你认为哪个年级的学生对党史知识掌握的总体水平较好,并说明理由.
5、一个不透明口袋里装有4个除颜色外其他完全相同的球,其中红球2个,黄球1个,白球1个.
(1)从中任取一个球,求摸到红球的概率;
(2)若第一次从口袋中任意摸出1个球,不放回,第二次再摸出1个球.用列表或画树状图写出所有可能性,并求出刚好摸到一个红球和一个白球的概率.【版权所有:21教育】
-参考答案-
一、单选题
1、C
【解析】
【分析】
根据必然事件、不可能事件、随机事件的定义 ( http: / / www.21cnjy.com )依次判断即可得出答案.,必然事件和不可能事件统称确定性事件;必然事件:在一定条件下,一定会发生的事件称为必然事件;不可能事件:在一定条件下,一定不会发生的事件称为不可能事件;随机事件:在一定条件下,可能发生也可能不发生的事件称为随机事件.21·世纪*教育网
【详解】
解:A、可能性很大的事情不一定是必然发生的,故本选项错误;
B、可能性很小的事情不一定是不可能发生的,故本选项错误;
C、如果圆的半径为,则该圆的周长为是必然的,故本选项正确;
D、冬季里下雪是随机事件,故本选项错误.
故选C.
【点睛】
本题主要考查了必然事件、不可能事件、随机事件的定义,难度适中.
2、B
【解析】
【分析】
根据随机事件的概率值即可判断.
【详解】
解:因为不可能事件的概率为0,0<随机事件的概率<1,必然事件的概率为1,
所以在如图的各事件中,是随机事件的有:事件B和事件C,共有2个,
故选:B.
【点睛】
本题考查了随机事件,弄清不可能事件的概率,随机事件的概率,必然事件的概率是解题的关键.
3、B
【解析】
【分析】
利用大量重复实验时,事件 ( http: / / www.21cnjy.com )发生的频率在某个固定位置左右摆动,并且摆动的幅度越来越小,根据这个频率稳定性定理,可以用频率的集中趋势来估计概率,这个固定的近似值就是这个事件的概率.
【详解】
解:∵通过大量重复试验后发现,摸到红球的频率稳定于0.4,
∴n=4÷0.4,
解得:n=10.
故选B.
【点睛】
此题考查利用频率估计概率,掌握运算法则是解题关键.
4、A
【解析】
【分析】
在同样条件下,大量反复试验时,随机事件发生的频率逐渐稳定在概率附近,可以从比例关系入手,设袋中有白色乒乓球x个,列出方程求解即可.21教育网
【详解】
解:设袋中有白色乒乓球x个,由题意得=0.3,
解得x=21.
故选:A.
【点睛】
本题利用了用大量试验得到的频率可以估计事件的概率.关键是利用黄球的概率公式列方程求解得到黄球的个数.21cnjy.com
5、C
【解析】
【分析】
根据必然事件是一定会发生的事件这个概念求解即可.
【详解】
解:选项A:某种彩票中奖率为1%,则买100张这种彩票必然中奖,不一定必然中奖,不合题意;
选项B:今晚努力学习,明天考试必然考出好成绩,是随机事件,不合题意;
选项C:从装有2个红球、3个白球的袋中随机摸出4个球,则一定会摸出红球,是必然事件,符合题意;
选项D:抛掷一枚普通的骰子所得的点数一定小于6,也有可能等于6,故此选项不合题意;
故选:C.
【点睛】
此题主要考查了随机事件,熟练掌握必然事件的概念是解题关键.
6、C
【解析】
【分析】
根据圆周角可得1区域的圆心角度数,然后计算各个区域的可能性,比较大小即可得.
【详解】
解:1区域的圆心角为:,
∴落在1区域的可能性为:,
落在2区域的可能性为:,
落在3区域的可能性为:,
落在4区域的可能性为:,
∵,
∴落在3区域的可能性最大,
故选:C.
【点睛】
题目主要考查可能性的计算及大小比较,理解题意,掌握可能性的计算方法是解题关键.
7、B
【解析】
【分析】
根据概率公式计算简单概率即可.
【详解】
由于显示屏每间隔4分钟显示一次火车班次的信息,显示时间持续1分钟,
所以显示屏上每隔5分钟就有一分钟的显示时间,
某人到达该车站时正好显示火车班次信息的概率是.
故选B.
【点睛】
本题考查简单的概率,概率=所求情况数与总情况数之比.
8、D
【解析】
【分析】
先根据题意得列出表格,可得共有12种等可能结果,抽到的两张卡片上都恰好印的既是中心对称又是轴对称的图形的有6种,再根据概率公式,即可求解.
【详解】
解: 根据题意得列出表格如下:
平行四边形 矩形 菱形 正方形
平行四边形 矩形、平行四边形 菱形、平行四边形 正方形、平行四边形
矩形 平行四边形、矩形 菱形、矩形 正方形、矩形
菱形 平行四边形、菱形 矩形、菱形 正方形、菱形
正方形 平行四边形、正方形 矩形、正方形 菱形、正方形
∵不平行四边形是中心对称图形,矩形、菱形、正方形既是中心对称又是轴对称的图形,
∴共有12种等可能结果,抽到的两张卡片上都恰好印的既是中心对称又是轴对称的图形的有6种,
∴抽到的两张卡片上都恰好印的既是中心对称又是轴对称的图形的概率为.
故选:D
【点睛】
本题主要考查了利用画树状图或列表格求概率,能根据题意画出树状图或列出表格是解题的关键.
9、D
【解析】
【分析】
根据随机事件,必然事件,不可能事件的定义判断即可.
【详解】
解:一个不透明的盒子中有100个红色小球,10个白色小球,1个黄色小球,现从中随机取出一个球,
可能取出的是红色小球,也可能取出的是白色小球,也可能取出的是黄色小球,
不可能取出的是黑色小球,
所以:取出的是黑色小球是不可能事件,
故选:D.
【点睛】
本题考查了随机事件,解题的关键是熟练掌握随机事件,必然事件,不可能事件的概念.
10、C
【解析】
【分析】
根据事件的概念:事件分为确定事件和不确定事件(随机事件),确定事件又分为必然事件和不可能事件,①必然事件发生的概率为1,即(必然事件);②不可能事件发生的概率为0,即(不可能事件);③如果为不确定事件(随机事件),那么(A),逐一判断即可得到答案.
【详解】
解:①不可能事件发生的概率为0,说法正确;
②随机事件发生的概率为0到1,故说法错误;
③事件发生的概率与实验次数无关,故说法正确;
④“画一个矩形,其对角线互相垂直”是随机事件,故说法错误.
正确的说法有:①③.
故选:.
【点睛】
本题考查的是必然事件、不可能事件、随机事件的概念,掌握其概念是解决此题关键.
二、填空题
1、
【解析】
【分析】
画树状图,共有4种等可能的结果,两次摸到的球是一白一红的结果有2种,再由概率公式求解即可.
【详解】
解:画树状图如下:
( http: / / www.21cnjy.com / )
共有4种等可能的结果,两次摸到的球是一白一红的结果有2种,
∴两次摸到的球是一白一红的概率为,
故答案为:.
【点睛】
本题考查的是用列表法或画树状图法求概率.列表 ( http: / / www.21cnjy.com )法或画树状图法可以不重复不遗漏的列出所有可能的结果,列表法适合于两步完成的事件,树状图法适合两步或两步以上完成的事件.注意概率=所求情况数与总情况数之比.21·cn·jy·com
2、0.3
【解析】
【分析】
根据频数、总数与频率关系公式为,计算即可.
【详解】
解:∵成绩在80.5~90.5(分)这一组的频数是15,总数为50,
∴频率为:.
故答案为0.3.
【点睛】
本题考查频率的求法,掌握频数、总数与频率之间关系是解题关键.
3、0.2
【解析】
【分析】
根据各小组频数之和等于数据总和,即可求得第三组的频数;再根据频率=频数÷总数,进行计算.
【详解】
解:根据题意,得
第三组数据的个数x=50-(8+15+12+5)=10,
故第四组的频率为10÷50=0.2.
故答案为:0.2.
【点睛】
本题是对频率、频数灵活运用的综合考查.注意:各小组频数之和等于数据总和,各小组频率之和等于1.
4、
【解析】
【分析】
求得阴影部分的面积后除以正方形的面积即可求得概率.
【详解】
解:设圆O的半径为a,则正方形ABCD的边长为2a.
由题意可得,阴影部分的面积=正方形的面积-圆的面积
=(2a)2-πa2
=4a2-πa2
=(4-π)a2,
∴米粒落在阴影部分的概率是=.
故答案为:
【点睛】
本题考查了几何概率,熟练掌握正方形与圆的面积公式及概率公式是解题的关键.
5、
【解析】
【分析】
先画出树状图,从而可得的所有等可能的结果,再找出在第四象限的结果,然后利用概率公式进行计算即可得.【出处:21教育名师】
【详解】
解:画出树状图如下:
( http: / / www.21cnjy.com / )
由此可知,的所有等可能的结果共有12种,其中,在第四象限的结果有3种,
则在第四象限的概率为,
故答案为:.
【点睛】
本题考查了利用列举法求概率,正确画出树状图是解题关键.
三、解答题
1、 (1)或
(2)
【解析】
【分析】
(1)由出发,把构成三角形为等腰三角形的情况例举出来,再计算其面积即可;
(2)利用画树状图的方法得到所有的等可能的结果数与符合条件的结果数,再利用概率公式进行计算即可.
(1)
解:由出发,构成三角形为等腰三角形的情况有:
等腰三角形的形状是两种等腰直角三角形,面积分别为
所以该等腰三角形的面积所有可能的值为或
故答案为:或
(2)
解:如图,
( http: / / www.21cnjy.com / )
由树状图可得,所有的等可能的结果数有种,而符合条件的结果数只有1种,
所以对于一个不知道该密码的人,其一次尝试能将小明手机解锁的概率为
【点睛】
本题考查的是利用例举法与画树状图的方法 ( http: / / www.21cnjy.com )求解所有的等可能的结果数,利用概率公式计算等可能事件的概率,勾股定理的应用,掌握“例举法与画树状图的方法”是解本题的关键.
2、
【解析】
【分析】
画树状图,共有12种等可能的结果,其中所选2人都是女生的有2种,再由概率公式求解即可.
【详解】
解:画树状图如下:
( http: / / www.21cnjy.com / )
共有12种等可能的结果,其中所选2人都是女生的有2种,即、,
(所选代表都是女生).
【点睛】
此题考查的是用树状图法求概率,解题的关键是掌握树状图法可以不重复不遗漏的列出所有可能的结果,适合两步或两步以上完成的事件;注意概率所求情况数与总情况数之比.
3、 (1)他选中《孙子算经》的概率为
(2)其中1部是《周髀算经》的概率为
【解析】
(1)
小华想从这4部数学名著中随机选择1部阅读,
则他选中《孙子算经》的概率为.
(2)
将四部名著《周髀算经》,《九章算术》,《海岛算经》,《孙子算经》分别记为A,B,C,D,
记其中1部是《周髀算经》为事件M.
用列表法列举出从4部名著中选择2部所能产生的全部结果:
第1部第2部 A B C D
A
B
C
D
由表中可以看出,所有可能的结果有12种,并且它们出现的可能性相等.
其中事件M的结果有6种,即BA,CA,DA,AB,AC,AD,
.
【点睛】
本题考查了公式法求简单概 ( http: / / www.21cnjy.com )率,列表法求概率,列表法或画树状图法可以不重复不遗漏的列出所有可能的结果数,概率=所求情况数与总情况数之比.熟练掌握求概率的方法是解题的关键.
4、 (1)
(2)100
(3)八年级的学生对党史知识掌握的总体水平较好,理由见解析
【解析】
【分析】
(1)将七、八年级的成绩排列好,找到八年级的成绩中70≤x<80和80≤x<90的人数,即可求得,根据众数的定义,从七年级成绩中找到出现次数最多的那个数,即可求得,根据中位数的定义,在八年级成绩中找到中间位置的数,即第8个数,即可求得;2·1·c·n·j·y
(2)根据表格可知八年级90分以上 ( http: / / www.21cnjy.com )学生人数,求得所占的百分比,然后列式计算即可;(3)七、八年级的平均成绩相等,而八年级的中位数为83,七年级的中位数为81,根据中位数的大小判断八年成绩较好www-2-1-cnjy-com
(1)
七年级成绩从小到大排列:58,64,7 ( http: / / www.21cnjy.com )4,76,80,80,80,81,82,85,85,89,90,92,99,其中80出现3次,次数最多21教育名师原创作品
则众数为:80,故
八年级成绩从小到大排列:46,72,76,80,80,82,82,83,83,83,85,88,91,92,92,第8个数即为中位数,是:83,故21*cnjy*com
其中70≤x<80的有2人,则,80≤x<90的有9人,则
故答案为:
(2)
(人)
故答案为:100
(3)
八年级的总体水平较好,理由如下:
七、八年级的平均成绩相等,而八年 ( http: / / www.21cnjy.com )级的中位数为83,七年级的中位数为81,83>81 八年级的学生对党史知识掌握的总体水平较好(答案不唯一,合理即可)
【点睛】
本题主要考查了数据的统计、求中位数以及运用中位数进行决策、用样本估计总体等知识点,正确的统计是基础、灵活应用相关知识是解答本题的关键
5、 (1)
(2)
【解析】
【分析】
(1)直接根据概率公式求解即可;
(2)根据概率公式画出树状图得出所有等可能的情况数,找出符合条件的情况数,然后根据概率公式即可得出答案.
(1)
解:∵不透明口袋里装有4个除颜色外其他完全相同的球,其中红球2个,黄球1个,白球1个,
∴从中任取一个球,求摸到红球的概率是;
(2)
根据题意画图如下:
( http: / / www.21cnjy.com / )
共有12种等可能的情况数,其中刚好摸到一个红球和一个白球的情况数有4种,、
则刚好摸到一个红球和一个白球的概率是.
【点睛】
此题考查的是树状图法求概 ( http: / / www.21cnjy.com )率.树状图法可以不重复不遗漏的列出所有可能的结果,适合两步或两步以上完成的事件;用到的知识点为:概率=所求情况数与总情况数之比.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
九年级数学下册第6章事件的概率章节练习
考试时间:90分钟;命题人:数学教研组
考生注意:
1、本卷分第I卷(选择题)和第Ⅱ卷(非选择题)两部分,满分100分,考试时间90分钟
2、答卷前,考生务必用0.5毫米黑色签字笔将自己的姓名、班级填写在试卷规定位置上
3、答案必须写在试卷各个题目指定 ( http: / / www.21cnjy.com )区域内相应的位置,如需改动,先划掉原来的答案,然后再写上新的答案;不准使用涂改液、胶带纸、修正带,不按以上要求作答的答案无效。21世纪教育网版权所有
第I卷(选择题 30分)
一、单选题(10小题,每小题3分,共计30分)
1、下列说法中,正确的是( )
A.可能性很大的事情是必然发生的
B.可能性很小的事情是不可能发生的
C.如果圆的半径为,则该圆的周长为是必然的
D.冬季里下雪是一定发生的
2、在下图的各事件中,是随机事件的有( )
A.1个 B.2个 C.3个 D.4个
3、在一个不透明的盒子中装 ( http: / / www.21cnjy.com )有n个小球,它们除了颜色不同外,其余都相同,其中有4个白球.每次试验前,将盒子中的小球摇匀,随机摸出一个球记下颜色后再放回盒中.大量重复上述试验后发现,摸到白球的频率稳定于0.4,则n的值为( )【来源:21·世纪·教育·网】
A.6 B.10 C.14 D.18
4、在一个不透明的盒子中装有30个白、黄两种 ( http: / / www.21cnjy.com )颜色的乒乓球,这些乒乓球除颜色外都相同. 班长进行了多次的摸球试验,发现摸到黄色乒乓球的频率稳定在0.3左右,则盒子中的白色乒乓球的个数可能是( )2-1-c-n-j-y
A.21个 B.15个 C.12个 D.9个
5、下列事件是必然事件的是( )
A.某种彩票中奖率为1%,则买100张这种彩票必然中奖
B.今晚努力学习,明天考试必然考出好成绩
C.从装有2个红球、3个白球的袋中随机摸出4个球,则一定会摸出红球
D.抛掷一枚普通的骰子所得的点数一定小于6
6、如图是一个游戏转盘.自由转动转盘,当转盘停止转动后,指针落在数字1,2,3,4所示区域内可能性最大的是( )【来源:21cnj*y.co*m】
( http: / / www.21cnjy.com / )
A.1号 B.2号 C.3号 D.4号
7、某火车站的显示屏每间隔 ( http: / / www.21cnjy.com )4分钟显示一次火车班次的信息,显示时间持续1分钟,某人到达该车站时,显示屏正好显示火车班次信息的概率是( )
A. B. C. D.
8、有4张背面相同的卡片,正面分别印有 ( http: / / www.21cnjy.com )平行四边形、矩形、菱形、正方形,现将4张卡片正面朝下一字摆开,从中随机抽取两张,抽到的两张卡片上都恰好印的既是中心对称又是轴对称的图形的概率为( )
A.1 B. C. D.
9、一个不透明的盒子中有100个红色小球,10个白色小球,1个黄色小球,现从中随机取出一个球,下列事件是不可能事件的是( )
A.取出的是红色小球 B.取出的是白色小球
C.取出的是黄色小球 D.取出的是黑色小球
10、下列说法:①不可能事件发生的概率为0;②随机事件发生的概率为;③事件发生的概率与实验次数无关;④“画一个矩形,其对角线互相垂直”是必然事件.其中正确的是( )
A.①② B.②③ C.①③ D.①④
第Ⅱ卷(非选择题 70分)
二、填空题(5小题,每小题4分,共计20分)
1、一个布袋里装有2个只有颜 ( http: / / www.21cnjy.com )色不同的球,其中1个红球,1个白球,从布袋里摸出1个球,记下颜色后放回,搅匀,再摸出1个球,则两次摸到的球恰好颜色不同的概率是______.
2、杨老师对自己所教班级( ( http: / / www.21cnjy.com )共50名学生)的一次数学测验成绩进行统计.结果是:成绩在80.5~90.5(分)这一组的频数是15,那么本班成绩在80.5~90.5分之间的频率是__________.
3、把50个数据分成五组,第一、二、三、四、五组的数据个数分别是8,15,x,12,5,则第三组的频率为______.
4、如图,⊙O与正方形ABC ( http: / / www.21cnjy.com )D各边相切,若随机向正方形内投一粒米(将米粒看成一个点),则米粒落在阴影部分的概率是__________________.
( http: / / www.21cnjy.com / )
5、现将背面完全相同,正面分别标 ( http: / / www.21cnjy.com )有数﹣1,1,2,3的四张卡片洗匀后,背面朝上,从中任取一张,将该卡片上的数标记为m,再从剩下的三张卡片中任取一张,将该卡片上的数记为n,则P(m,n)在第四象限的概率为_____.
三、解答题(5小题,每小题10分,共计50分)
1、在如今手机的功能中,都可以利用手势密码进行锁屏和解锁.其中最常见的就是利用的正方形点阵设置密码,我们将其称为“9点码”.通常,在设置“9点码”时,只能连接相邻的两点(如图,不妨将9个点依次对应数字1到9;例如图中路线Ⅰ,Ⅱ等是可行的,路线Ⅲ,Ⅳ是不可行的),不能走重复的路线,从而形成相应的密码线段,线段越多,密码越复杂.已知小明设置的“9点码”从右上角的点“3”出发,且用了3个数字.
( http: / / www.21cnjy.com / )
(1)已知横向和纵向的相邻两点距离为1, ( http: / / www.21cnjy.com )且小明设置的“9点码”的密码线段恰好构成了一个等腰三角形,则该等腰三角形的面积所有可能的值为______;
(2)用概率知识并结合树状图回答 ( http: / / www.21cnjy.com ):若小明设置的“9点码”用了3个数字,对于一个不知道该密码的人,通过画树状图,求其一次尝试能将小明手机解锁的概率.
2、某市准备举行初中生“党史知识竞赛” ( http: / / www.21cnjy.com ),学校通过初赛选出了2位男生A、B和2位女生C、D共4位选手,准备从4人中任选2人代表学校参加比赛.求所选代表都是女生的概率.
3、中国古代有着辉煌的数学成就,《周髀算经》,《九章算术》,《海岛算经》,《孙子算经》等是了解我国古代数学的重要文献.
(1)小华想从这4部数学名著中随机选择1部阅读,求他选中《孙子算经》的概率;
(2)某中学拟从这4部数学 ( http: / / www.21cnjy.com )名著中选择2部作为“数学文化”校本课程学习内容,用列表法或树状图法求出选中的2部名著中,其中1部是《周髀算经》的概率.
4、为迎接中国共产党建党100周年, ( http: / / www.21cnjy.com )某校组织七、八年级学生开展了党史知识竞赛.现从两个年级各随机抽取15名学生的竞赛成绩(百分制)进行分析,过程如下:21*cnjy*com
【收集数据】
七年级:89,74,85,80,81,92,58,99,80,82,90,76,80,85,64.
八年级:91,72,92,80,83,92,88,82,85,83,76,83,82,80,46.
【整理数据】
40≤x<50 50≤x<60 60≤x<70 70≤x<80 80≤x<90 90≤x<100
七年级 0 1 1 2 8 3
八年级 1 0 0 a b 3
【分析数据】
平均数 众数 中位数
七年级 81 c 81
八年级 81 83 d
【应用数据】
(1)由如表填空:a= ,b= ,c= ,d= .
(2)若八年级有500名学生,请你估计该校八年级学生在本次竞赛中成绩在90分以上(含90分)的有 人.www.21-cn-jy.com
(3)你认为哪个年级的学生对党史知识掌握的总体水平较好,并说明理由.
5、一个不透明口袋里装有4个除颜色外其他完全相同的球,其中红球2个,黄球1个,白球1个.
(1)从中任取一个球,求摸到红球的概率;
(2)若第一次从口袋中任意摸出1个球,不放回,第二次再摸出1个球.用列表或画树状图写出所有可能性,并求出刚好摸到一个红球和一个白球的概率.【版权所有:21教育】
-参考答案-
一、单选题
1、C
【解析】
【分析】
根据必然事件、不可能事件、随机事件的定义 ( http: / / www.21cnjy.com )依次判断即可得出答案.,必然事件和不可能事件统称确定性事件;必然事件:在一定条件下,一定会发生的事件称为必然事件;不可能事件:在一定条件下,一定不会发生的事件称为不可能事件;随机事件:在一定条件下,可能发生也可能不发生的事件称为随机事件.21·世纪*教育网
【详解】
解:A、可能性很大的事情不一定是必然发生的,故本选项错误;
B、可能性很小的事情不一定是不可能发生的,故本选项错误;
C、如果圆的半径为,则该圆的周长为是必然的,故本选项正确;
D、冬季里下雪是随机事件,故本选项错误.
故选C.
【点睛】
本题主要考查了必然事件、不可能事件、随机事件的定义,难度适中.
2、B
【解析】
【分析】
根据随机事件的概率值即可判断.
【详解】
解:因为不可能事件的概率为0,0<随机事件的概率<1,必然事件的概率为1,
所以在如图的各事件中,是随机事件的有:事件B和事件C,共有2个,
故选:B.
【点睛】
本题考查了随机事件,弄清不可能事件的概率,随机事件的概率,必然事件的概率是解题的关键.
3、B
【解析】
【分析】
利用大量重复实验时,事件 ( http: / / www.21cnjy.com )发生的频率在某个固定位置左右摆动,并且摆动的幅度越来越小,根据这个频率稳定性定理,可以用频率的集中趋势来估计概率,这个固定的近似值就是这个事件的概率.
【详解】
解:∵通过大量重复试验后发现,摸到红球的频率稳定于0.4,
∴n=4÷0.4,
解得:n=10.
故选B.
【点睛】
此题考查利用频率估计概率,掌握运算法则是解题关键.
4、A
【解析】
【分析】
在同样条件下,大量反复试验时,随机事件发生的频率逐渐稳定在概率附近,可以从比例关系入手,设袋中有白色乒乓球x个,列出方程求解即可.21教育网
【详解】
解:设袋中有白色乒乓球x个,由题意得=0.3,
解得x=21.
故选:A.
【点睛】
本题利用了用大量试验得到的频率可以估计事件的概率.关键是利用黄球的概率公式列方程求解得到黄球的个数.21cnjy.com
5、C
【解析】
【分析】
根据必然事件是一定会发生的事件这个概念求解即可.
【详解】
解:选项A:某种彩票中奖率为1%,则买100张这种彩票必然中奖,不一定必然中奖,不合题意;
选项B:今晚努力学习,明天考试必然考出好成绩,是随机事件,不合题意;
选项C:从装有2个红球、3个白球的袋中随机摸出4个球,则一定会摸出红球,是必然事件,符合题意;
选项D:抛掷一枚普通的骰子所得的点数一定小于6,也有可能等于6,故此选项不合题意;
故选:C.
【点睛】
此题主要考查了随机事件,熟练掌握必然事件的概念是解题关键.
6、C
【解析】
【分析】
根据圆周角可得1区域的圆心角度数,然后计算各个区域的可能性,比较大小即可得.
【详解】
解:1区域的圆心角为:,
∴落在1区域的可能性为:,
落在2区域的可能性为:,
落在3区域的可能性为:,
落在4区域的可能性为:,
∵,
∴落在3区域的可能性最大,
故选:C.
【点睛】
题目主要考查可能性的计算及大小比较,理解题意,掌握可能性的计算方法是解题关键.
7、B
【解析】
【分析】
根据概率公式计算简单概率即可.
【详解】
由于显示屏每间隔4分钟显示一次火车班次的信息,显示时间持续1分钟,
所以显示屏上每隔5分钟就有一分钟的显示时间,
某人到达该车站时正好显示火车班次信息的概率是.
故选B.
【点睛】
本题考查简单的概率,概率=所求情况数与总情况数之比.
8、D
【解析】
【分析】
先根据题意得列出表格,可得共有12种等可能结果,抽到的两张卡片上都恰好印的既是中心对称又是轴对称的图形的有6种,再根据概率公式,即可求解.
【详解】
解: 根据题意得列出表格如下:
平行四边形 矩形 菱形 正方形
平行四边形 矩形、平行四边形 菱形、平行四边形 正方形、平行四边形
矩形 平行四边形、矩形 菱形、矩形 正方形、矩形
菱形 平行四边形、菱形 矩形、菱形 正方形、菱形
正方形 平行四边形、正方形 矩形、正方形 菱形、正方形
∵不平行四边形是中心对称图形,矩形、菱形、正方形既是中心对称又是轴对称的图形,
∴共有12种等可能结果,抽到的两张卡片上都恰好印的既是中心对称又是轴对称的图形的有6种,
∴抽到的两张卡片上都恰好印的既是中心对称又是轴对称的图形的概率为.
故选:D
【点睛】
本题主要考查了利用画树状图或列表格求概率,能根据题意画出树状图或列出表格是解题的关键.
9、D
【解析】
【分析】
根据随机事件,必然事件,不可能事件的定义判断即可.
【详解】
解:一个不透明的盒子中有100个红色小球,10个白色小球,1个黄色小球,现从中随机取出一个球,
可能取出的是红色小球,也可能取出的是白色小球,也可能取出的是黄色小球,
不可能取出的是黑色小球,
所以:取出的是黑色小球是不可能事件,
故选:D.
【点睛】
本题考查了随机事件,解题的关键是熟练掌握随机事件,必然事件,不可能事件的概念.
10、C
【解析】
【分析】
根据事件的概念:事件分为确定事件和不确定事件(随机事件),确定事件又分为必然事件和不可能事件,①必然事件发生的概率为1,即(必然事件);②不可能事件发生的概率为0,即(不可能事件);③如果为不确定事件(随机事件),那么(A),逐一判断即可得到答案.
【详解】
解:①不可能事件发生的概率为0,说法正确;
②随机事件发生的概率为0到1,故说法错误;
③事件发生的概率与实验次数无关,故说法正确;
④“画一个矩形,其对角线互相垂直”是随机事件,故说法错误.
正确的说法有:①③.
故选:.
【点睛】
本题考查的是必然事件、不可能事件、随机事件的概念,掌握其概念是解决此题关键.
二、填空题
1、
【解析】
【分析】
画树状图,共有4种等可能的结果,两次摸到的球是一白一红的结果有2种,再由概率公式求解即可.
【详解】
解:画树状图如下:
( http: / / www.21cnjy.com / )
共有4种等可能的结果,两次摸到的球是一白一红的结果有2种,
∴两次摸到的球是一白一红的概率为,
故答案为:.
【点睛】
本题考查的是用列表法或画树状图法求概率.列表 ( http: / / www.21cnjy.com )法或画树状图法可以不重复不遗漏的列出所有可能的结果,列表法适合于两步完成的事件,树状图法适合两步或两步以上完成的事件.注意概率=所求情况数与总情况数之比.21·cn·jy·com
2、0.3
【解析】
【分析】
根据频数、总数与频率关系公式为,计算即可.
【详解】
解:∵成绩在80.5~90.5(分)这一组的频数是15,总数为50,
∴频率为:.
故答案为0.3.
【点睛】
本题考查频率的求法,掌握频数、总数与频率之间关系是解题关键.
3、0.2
【解析】
【分析】
根据各小组频数之和等于数据总和,即可求得第三组的频数;再根据频率=频数÷总数,进行计算.
【详解】
解:根据题意,得
第三组数据的个数x=50-(8+15+12+5)=10,
故第四组的频率为10÷50=0.2.
故答案为:0.2.
【点睛】
本题是对频率、频数灵活运用的综合考查.注意:各小组频数之和等于数据总和,各小组频率之和等于1.
4、
【解析】
【分析】
求得阴影部分的面积后除以正方形的面积即可求得概率.
【详解】
解:设圆O的半径为a,则正方形ABCD的边长为2a.
由题意可得,阴影部分的面积=正方形的面积-圆的面积
=(2a)2-πa2
=4a2-πa2
=(4-π)a2,
∴米粒落在阴影部分的概率是=.
故答案为:
【点睛】
本题考查了几何概率,熟练掌握正方形与圆的面积公式及概率公式是解题的关键.
5、
【解析】
【分析】
先画出树状图,从而可得的所有等可能的结果,再找出在第四象限的结果,然后利用概率公式进行计算即可得.【出处:21教育名师】
【详解】
解:画出树状图如下:
( http: / / www.21cnjy.com / )
由此可知,的所有等可能的结果共有12种,其中,在第四象限的结果有3种,
则在第四象限的概率为,
故答案为:.
【点睛】
本题考查了利用列举法求概率,正确画出树状图是解题关键.
三、解答题
1、 (1)或
(2)
【解析】
【分析】
(1)由出发,把构成三角形为等腰三角形的情况例举出来,再计算其面积即可;
(2)利用画树状图的方法得到所有的等可能的结果数与符合条件的结果数,再利用概率公式进行计算即可.
(1)
解:由出发,构成三角形为等腰三角形的情况有:
等腰三角形的形状是两种等腰直角三角形,面积分别为
所以该等腰三角形的面积所有可能的值为或
故答案为:或
(2)
解:如图,
( http: / / www.21cnjy.com / )
由树状图可得,所有的等可能的结果数有种,而符合条件的结果数只有1种,
所以对于一个不知道该密码的人,其一次尝试能将小明手机解锁的概率为
【点睛】
本题考查的是利用例举法与画树状图的方法 ( http: / / www.21cnjy.com )求解所有的等可能的结果数,利用概率公式计算等可能事件的概率,勾股定理的应用,掌握“例举法与画树状图的方法”是解本题的关键.
2、
【解析】
【分析】
画树状图,共有12种等可能的结果,其中所选2人都是女生的有2种,再由概率公式求解即可.
【详解】
解:画树状图如下:
( http: / / www.21cnjy.com / )
共有12种等可能的结果,其中所选2人都是女生的有2种,即、,
(所选代表都是女生).
【点睛】
此题考查的是用树状图法求概率,解题的关键是掌握树状图法可以不重复不遗漏的列出所有可能的结果,适合两步或两步以上完成的事件;注意概率所求情况数与总情况数之比.
3、 (1)他选中《孙子算经》的概率为
(2)其中1部是《周髀算经》的概率为
【解析】
(1)
小华想从这4部数学名著中随机选择1部阅读,
则他选中《孙子算经》的概率为.
(2)
将四部名著《周髀算经》,《九章算术》,《海岛算经》,《孙子算经》分别记为A,B,C,D,
记其中1部是《周髀算经》为事件M.
用列表法列举出从4部名著中选择2部所能产生的全部结果:
第1部第2部 A B C D
A
B
C
D
由表中可以看出,所有可能的结果有12种,并且它们出现的可能性相等.
其中事件M的结果有6种,即BA,CA,DA,AB,AC,AD,
.
【点睛】
本题考查了公式法求简单概 ( http: / / www.21cnjy.com )率,列表法求概率,列表法或画树状图法可以不重复不遗漏的列出所有可能的结果数,概率=所求情况数与总情况数之比.熟练掌握求概率的方法是解题的关键.
4、 (1)
(2)100
(3)八年级的学生对党史知识掌握的总体水平较好,理由见解析
【解析】
【分析】
(1)将七、八年级的成绩排列好,找到八年级的成绩中70≤x<80和80≤x<90的人数,即可求得,根据众数的定义,从七年级成绩中找到出现次数最多的那个数,即可求得,根据中位数的定义,在八年级成绩中找到中间位置的数,即第8个数,即可求得;2·1·c·n·j·y
(2)根据表格可知八年级90分以上 ( http: / / www.21cnjy.com )学生人数,求得所占的百分比,然后列式计算即可;(3)七、八年级的平均成绩相等,而八年级的中位数为83,七年级的中位数为81,根据中位数的大小判断八年成绩较好www-2-1-cnjy-com
(1)
七年级成绩从小到大排列:58,64,7 ( http: / / www.21cnjy.com )4,76,80,80,80,81,82,85,85,89,90,92,99,其中80出现3次,次数最多21教育名师原创作品
则众数为:80,故
八年级成绩从小到大排列:46,72,76,80,80,82,82,83,83,83,85,88,91,92,92,第8个数即为中位数,是:83,故21*cnjy*com
其中70≤x<80的有2人,则,80≤x<90的有9人,则
故答案为:
(2)
(人)
故答案为:100
(3)
八年级的总体水平较好,理由如下:
七、八年级的平均成绩相等,而八年 ( http: / / www.21cnjy.com )级的中位数为83,七年级的中位数为81,83>81 八年级的学生对党史知识掌握的总体水平较好(答案不唯一,合理即可)
【点睛】
本题主要考查了数据的统计、求中位数以及运用中位数进行决策、用样本估计总体等知识点,正确的统计是基础、灵活应用相关知识是解答本题的关键
5、 (1)
(2)
【解析】
【分析】
(1)直接根据概率公式求解即可;
(2)根据概率公式画出树状图得出所有等可能的情况数,找出符合条件的情况数,然后根据概率公式即可得出答案.
(1)
解:∵不透明口袋里装有4个除颜色外其他完全相同的球,其中红球2个,黄球1个,白球1个,
∴从中任取一个球,求摸到红球的概率是;
(2)
根据题意画图如下:
( http: / / www.21cnjy.com / )
共有12种等可能的情况数,其中刚好摸到一个红球和一个白球的情况数有4种,、
则刚好摸到一个红球和一个白球的概率是.
【点睛】
此题考查的是树状图法求概 ( http: / / www.21cnjy.com )率.树状图法可以不重复不遗漏的列出所有可能的结果,适合两步或两步以上完成的事件;用到的知识点为:概率=所求情况数与总情况数之比.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
