第6章 频率与概率专题攻克试卷(含解析)
图片预览




文档简介
中小学教育资源及组卷应用平台
九年级数学下册第6章事件的概率专题攻克
考试时间:90分钟;命题人:数学教研组
考生注意:
1、本卷分第I卷(选择题)和第Ⅱ卷(非选择题)两部分,满分100分,考试时间90分钟
2、答卷前,考生务必用0.5毫米黑色签字笔将自己的姓名、班级填写在试卷规定位置上
3、答案必须写在试卷各个 ( http: / / www.21cnjy.com )题目指定区域内相应的位置,如需改动,先划掉原来的答案,然后再写上新的答案;不准使用涂改液、胶带纸、修正带,不按以上要求作答的答案无效。【出处:21教育名师】
第I卷(选择题 30分)
一、单选题(10小题,每小题3分,共计30分)
1、在一个不透明的盒子里,装有若干个除颜色不同外其余都相同的小球,如果盒子中装有4个红球且从中随机摸出一个球是红球的概率为,则盒子中小球个数为( )21*cnjy*com
A.15 B.12 C.10 D.8
2、下列说法正确的是( )
A.新冠肺炎疫情防控期间,复学学生的核酸检测适合采用抽样调查
B.程晨投篮投中的概率是0.6,说明他投10次篮球一定能中6次
C.“平分弦的直径必垂直于这条弦”是一个必然事件
D.“在一张纸上随意画两个直角三角形,这两个直角三角形相似”为随机事件
3、下列事件中是必然事件的是( )
A.任意一个三角形的外角和等于180°
B.一个数与它的相反数的和是0
C.明天会下雨
D.正月十五雪打灯
4、在一个不透明纸箱中放有除 ( http: / / www.21cnjy.com )了数字不同外,其它完全相同的2张卡片,分别标有数字1、2,从中任意摸出一张,放回搅匀后再任意摸出一张,两次摸出的数字之和为奇数的概率为( )
A. B. C. D.
5、在4张小卡片上分别写有实数0,,π,,从中随机抽取一张卡片,抽到无理数的概率是( )21cnjy.com
A. B. C. D.
6、下列各选项的事件中,是随机事件的是( )
A.向上抛的硬币会落下 B.打开电视机,正在播新闻
C.太阳从西边升起 D.长度分别为4、5、6的三条线段围成三角形
7、中国福利彩票“双色球”投注方法是每注选择 ( http: / / www.21cnjy.com )6个红色球号码(从1-33的33个数中选择)加一个蓝色球号码(从1-16中16个数中选择),若最近三期蓝色号码球的开奖结果都为奇数,则下一期蓝色球的开奖结果( )
A.还是奇数 B.一定是偶数
C.是偶数的概率大于是奇数的概率 D.是偶数的概率为
8、把一副普通扑克牌中13张黑桃牌洗匀后正面向下放在桌子上.从中随机抽取一张,抽出的牌上的数小于6的概率为( )
( http: / / www.21cnjy.com / )
A. B. C. D.
9、下列事件是必然事件的是( )
A.某种彩票中奖率为1%,则买100张这种彩票必然中奖
B.今晚努力学习,明天考试必然考出好成绩
C.从装有2个红球、3个白球的袋中随机摸出4个球,则一定会摸出红球
D.抛掷一枚普通的骰子所得的点数一定小于6
10、一个不透明的袋子中装有10个小球,其中 ( http: / / www.21cnjy.com )6个红球、4个绿球,这些小球除颜色外无其它差别.从袋子中随机摸出一个小球,则摸出的小球是红球的概率为( )
A. B. C. D.
第Ⅱ卷(非选择题 70分)
二、填空题(5小题,每小题4分,共计20分)
1、大数据分析技术为打赢疫 ( http: / / www.21cnjy.com )情防控阻击战发挥了重要作用,如图是小乐同学的健康码(绿码)示意图,用黑白打印机打印于边长为4cm的正方形区域内,为了估计图中黑色部分的总面积,在正方形区域内随机掷点,经过大量重复试验,发现点落入黑色部分的频率稳定在0.6左右,据此可以估计黑色部分的总面积约为 _____cm2.
( http: / / www.21cnjy.com / )
2、某植物种子在相同的条件下发芽试验的结果如下:
每批粒数 50 100 300 400 500 1000
发芽的频数 45 96 283 380 474 948
则该植物种子发芽的概率的估计值是______.(结果精确到0.01)
3、某博览馆有A,B两个入口和C,D,E三个出口,小明入馆游览,他从A口进E口出的概率是 _____.
4、现有四张卡片,正面分别写有汉字 ( http: / / www.21cnjy.com )“我”“爱”“中”“国”,反面是完全相同的五角星图案.现将背面朝上充分洗匀后,从中任意抽取2张,其正面文字恰好组成“爱国”字样的概率为__.
5、如图是某地2020年5月1~10日每天最高温度的折线统计图,由此图可知该地这10天中,出现气温为26℃的频率是 _____.www.21-cn-jy.com
( http: / / www.21cnjy.com / )
三、解答题(5小题,每小题10分,共计50分)
1、为了解七年级学生的期 ( http: / / www.21cnjy.com )中数学考试情况,随机抽查了部分同学的成绩(满分100分),整理并制作了不完整的统计表和统计图.请根据图表提供的信息,解答下列问题:【来源:21·世纪·教育·网】
( http: / / www.21cnjy.com / )
分数x分 频数 百分比
30 10%
90 n
m 40%
60 20%
(1)本次调查的学生总人数是______;
(2)求m、n的值,并补全频数分布直方图;
(3)若要绘制扇形统计图,求成绩在的学生所对应的扇形圆心角度数.
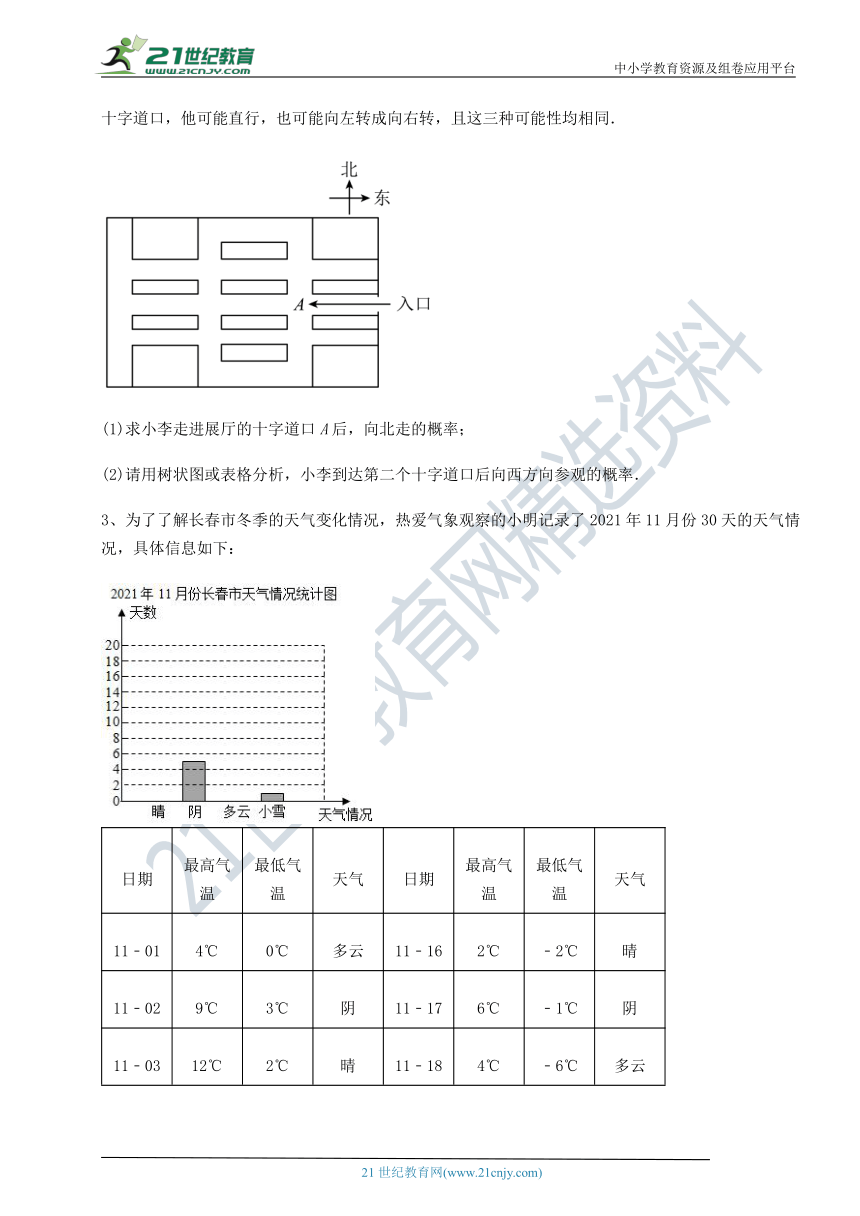
2、如图,是一个智慧教育产品的展销厅 ( http: / / www.21cnjy.com )的俯视示意图,小李进入展厅后,开始自由参观,每走到一个十字道口,他可能直行,也可能向左转成向右转,且这三种可能性均相同.21·世纪*教育网
( http: / / www.21cnjy.com / )
(1)求小李走进展厅的十字道口A后,向北走的概率;
(2)请用树状图或表格分析,小李到达第二个十字道口后向西方向参观的概率.
3、为了了解长春市冬季的天气变化情况,热爱气象观察的小明记录了2021年11月份30天的天气情况,具体信息如下:【来源:21cnj*y.co*m】
( http: / / www.21cnjy.com / )
日期 最高气温 最低气温 天气 日期 最高气温 最低气温 天气
11﹣01 4℃ 0℃ 多云 11﹣16 2℃ ﹣2℃ 晴
11﹣02 9℃ 3℃ 阴 11﹣17 6℃ ﹣1℃ 阴
11﹣03 12℃ 2℃ 晴 11﹣18 4℃ ﹣6℃ 多云
11﹣04 15℃ ﹣2℃ 阴 11﹣19 0℃ ﹣6℃ 多云
11﹣05 15℃ 10℃ 多云 11﹣20 0℃ ﹣7℃ 多云
11﹣06 2℃ ﹣6℃ 多云 11﹣21 ﹣4℃ ﹣9℃ 阴
11﹣07 ﹣3℃ ﹣4℃ 多云 11﹣22 ﹣8℃ ﹣12℃ 多云
11﹣08 9℃ ﹣4℃ 多云 11﹣23 ﹣8℃ ﹣15℃ 晴
11﹣09 ﹣3℃ ﹣6℃ 多云 11﹣24 ﹣7℃ ﹣14℃ 晴
11﹣10 ﹣2℃ ﹣5℃ 小雪 11﹣25 ﹣5℃ ﹣13℃ 多云
11﹣11 6℃ 2℃ 多云 11﹣26 ﹣3℃ ﹣13℃ 多云
11﹣12 ﹣1℃ ﹣7℃ 晴 11﹣27 0℃ ﹣1℃ 多云
11﹣13 4℃ ﹣6℃ 多云 11﹣28 6℃ ﹣4℃ 多云
11﹣14 12℃ 9℃ 阴 11﹣29 ﹣2℃ ﹣7℃ 多云
11﹣15 2℃ ﹣4℃ 晴 11﹣30 ﹣4℃ ﹣11℃ 多云
请你帮助小明同学把以上数据整理成统计图表.
2021年11月份长春市最低气温统计表
最低气温分组 频数 频率
10℃及10℃以上
大于等于5℃小于10℃
大于等于0℃小于5℃ 4
大于等于﹣5℃小于0℃ 9 0.3
大于等于﹣10℃小于﹣5℃ a
﹣10℃以下 b m
(1)补全条形统计图;
(2)2021年11月份长春市最低气温统计表中a= ;b= ;m= .
4、 “冰雪之约,中国之邀”, ( http: / / www.21cnjy.com )第24届冬季奥林匹克运动会即将在中国举行.某国家队计划从甲、乙两名短道速滑运动员中选派一人参赛(均取整数,单位:秒)如下:21教育名师原创作品
甲:37,41,38,40,39,37,39,42,37,40
乙:36,39,37,38,42,39,39,41,42,37
【整理数据】
甲成绩的扇形统计图(图1):
乙成绩的频数分布直方图(图2):
( http: / / www.21cnjy.com / )
【分析数据】
运动员 平均数 中位数 众数 方差
甲 39 a 37 c
乙 39 39 b 4
请根据以上信息,完成下列问题:
(1)甲成绩的中位数a落在扇形统计图的 部分(填A,B,C);
(2)请补全乙成绩的频数分布直方图;
(3)表中b= ,c= ;
【做出决策】
(4)根据甲、乙两人10次选拔比赛的成绩,你认为该国家队应选派哪位运动员参赛?并说明理由.
5、中国古代有着辉煌的数学成就,《周髀算经》,《九章算术》,《海岛算经》,《孙子算经》等是了解我国古代数学的重要文献.21世纪教育网版权所有
(1)小华想从这4部数学名著中随机选择1部阅读,求他选中《孙子算经》的概率;
(2)某中学拟从这4部数学名著中选择2 ( http: / / www.21cnjy.com )部作为“数学文化”校本课程学习内容,用列表法或树状图法求出选中的2部名著中,其中1部是《周髀算经》的概率.2·1·c·n·j·y
-参考答案-
一、单选题
1、B
【解析】
【分析】
设盒子中小球共有x个,根据概率公式得到,然后利用比例性质求出x即可.
【详解】
解:设盒子中小球共有x个,
根据题意得,
解得x=12,
经检验x=12是原方程的解,
所以盒子中小球共有12个.
故选:B.
【点睛】
本题考查了概率公式:随机事件A的概率P(A)=事件A可能出现的结果数除以所有可能出现的结果数.
2、D
【解析】
【分析】
本题需要根据调查事件的不同,选择需要全面普查还是抽样调查,根据事件本身判断事件是必然事件还是随机事件.
【详解】
解:A、对于传染疾病预防,应该对每一个人进行核酸检测,所以应选择普查的方式,选项说法错误,不符合题意;
B、程晨投篮投中的概率是0.6,说明他投10次篮球可能中6次,而非一定中6次,选项说法错误,不符合题意;
C、直径是特殊的弦,无论两条直径是否垂直都互相平分,所以这不是一个必然事件,选项说法错误,不符合题意;
D、在一张纸上随意画两个直角三角形,这两个直角三角形有可能相似,有可能不相似,所以为随机事件,选项说法正确,符合题意;
故选D.
【点睛】
本题考查统计方式的选择和必然事件,随机事件的判断,以及相似三角形的概念,根据题意选择适当的方式进行数据统计是解决本题的关键.
3、B
【解析】
【分析】
直接利用随机事件以及不可能事件、必然事件的定义分析得出答案.
【详解】
解:∵三角形的外角和等于360°,
∴任意一个三角形的外角和等于180°不是必然事件,是不可能事件,
∴A错误;
∵相反数的和为零,
∴一个数与它的相反数的和为0是必然事件,
故B正确;
∵明天会下雨是随机事件,不是必然事件,
故C错误;
∵正月十五雪打灯是随机事件,不是必然事件,
故D错误.
故选:B.
【点睛】
本题主要考查了随机事件、必然事件、不可能事件的定义,正确掌握相关定义是解题关键.
4、C
【解析】
【分析】
根据题意画出树状图求解即可.
【详解】
解:画树状图如下
( http: / / www.21cnjy.com / )
共有4种等可能的结果,两次摸出的数字之和为奇数的结果有2种
两次摸出的数字之和为奇数的概率为
故选:C.
【点睛】
此题考查了概率的问题,解题的关键是画出树状图求概率.
5、A
【解析】
【分析】
根据概率公式求解即可.
【详解】
解:∵从中随机抽取一张卡片,共有4种等可能结果,其中无理数的有1种可能结果,
∴抽到无理数的概率是,
故选:A.
【点睛】
本题主要考查概率公式,解题的关键是掌握无理数的概念和概率公式.
6、B
【解析】
【分析】
根据事件发生的可能性大小判断.
【详解】
解:A、向上抛的硬币会落下,是必然事件;
B、打开电视机,正在播新闻,是随机事件;
C、太阳从西边升起,是不可能事件;
D、长度分别为4、5、6的三条线段围成三角形,是必然事件;
故选:B.
【点睛】
本题考查的是必然事件、不可能事件、随机事件 ( http: / / www.21cnjy.com )的概念.必然事件指在一定条件下,一定发生的事件.不可能事件是指在一定条件下,一定不发生的事件,不确定事件即随机事件是指在一定条件下,可能发生也可能不发生的事件.21·cn·jy·com
7、D
【解析】
【分析】
分别求出下一期蓝色球的开奖结果是偶数的概率以及是奇数的概率,比较即可求解.
【详解】
解:由题意可知,蓝色球号码从1-16的16个数中选择,共有16种结果,1-16的16个数中偶数有8个,奇数有8个,
所以下一期蓝色球的开奖结果是偶数的概率为,
下一期蓝色球的开奖结果是奇数的概率为,
故选:D.
【点睛】
本题考查了概率公式,用到的知识点为:概率=所求情况数与总情况数之比.
8、D
【解析】
【分析】
共有13种等可能结果,小于6的有5种,利用概率公式计算即可.
【详解】
解:一副普通扑克牌中13张黑桃牌洗匀后正面向下放在桌子上.从中随机抽取一张,共有13种等可能结果,小于6的有5种,【版权所有:21教育】
抽出的牌上的数小于6的概率为,
故选:D.
【点睛】
本题考查了概率的求法,解题关键是熟记概率公式,准确列出所有可能.
9、C
【解析】
【分析】
根据必然事件是一定会发生的事件这个概念求解即可.
【详解】
解:选项A:某种彩票中奖率为1%,则买100张这种彩票必然中奖,不一定必然中奖,不合题意;
选项B:今晚努力学习,明天考试必然考出好成绩,是随机事件,不合题意;
选项C:从装有2个红球、3个白球的袋中随机摸出4个球,则一定会摸出红球,是必然事件,符合题意;
选项D:抛掷一枚普通的骰子所得的点数一定小于6,也有可能等于6,故此选项不合题意;
故选:C.
【点睛】
此题主要考查了随机事件,熟练掌握必然事件的概念是解题关键.
10、A
【解析】
【分析】
根据概率的求法,找准两点:①全部情况的总数;②符合条件的情况数目;二者的比值就是其发生的概率.
【详解】
解:∵一个不透明的袋子中装有10个小球,其中6个红球、4个绿球,
∴从袋子中随机摸出一个小球,则摸出的小球是红球的概率为.
故选:A.
【点睛】
本题考查概率的求法:如果一个事件有n种可能,而且这些事件的可能性相同,其中事件A出现m种结果,那么事件A的概率P(A)=.www-2-1-cnjy-com
二、填空题
1、9.6
【解析】
【分析】
先根据经过大量重复试验,发现点落入黑色部分的频率稳定在0.6左右,可估计点落入黑色部分的概率为0.6,再乘以正方形的面积即可得出答案.2-1-c-n-j-y
【详解】
解:∵经过大量重复试验,发现点落入黑色部分的频率稳定在0.6左右,
∴估计点落入黑色部分的概率为0.6,
∴估计黑色部分的总面积约为4×4×0.6=9.6(cm2),
故答案为:9.6.
【点睛】
本题主要考查利用频率估计概率,大 ( http: / / www.21cnjy.com )量重复实验时,事件发生的频率在某个固定位置左右摆动,并且摆动的幅度越来越小,根据这个频率稳定性定理,可以用频率的集中趋势来估计概率,这个固定的近似值就是这个事件的概率.
2、0.95
【解析】
【分析】
根据题意及频率估计概率可直接进行求解.
【详解】
解:由表格得:
当每批粒数为50时,则种子发芽的频率为;当每批粒数为100时,则种子发芽的频率为;当每批粒数为300时,则种子发芽的频率为;当每批粒数为400时,则种子发芽的频率为;当每批粒数为500时,则种子发芽的频率为;当每批粒数为1000时,则种子发芽的频率为;
∴该植物种子发芽的概率的估计值是0.95;
故答案为0.95.
【点睛】
本题主要考查利用频率估计概率,熟练掌握利用频率估计概率是解题的关键.
3、
【解析】
【分析】
画树状图,所有等可能的结果有6种,其中小明从A入口进,E出口出的有1种结果,再由概率公式求解即可.
【详解】
解:画树形图如图:
( http: / / www.21cnjy.com / )
由树形图可知,所有等可能的结果有6种,其中小明从A入口进,E出口出的有1种结果,
∴小明从A入口进,E出口出的概率为,
故答案为:.
【点睛】
本题考查的是树状图法求概率.树状 ( http: / / www.21cnjy.com )图法可以不重复不遗漏的列出所有可能的结果,适合两步或两步以上完成的事件;用到的知识点为:概率=所求情况数与总情况数之比.
4、
【解析】
【分析】
分别记“我”“爱”“中”“国”为A, ( http: / / www.21cnjy.com )B,C,D,利用树状图的方法可得所有等可能结果;再找到正面文字恰好组成“爱国”字样的结果数,利用概率公式计算可得.
【详解】
解:分别记“我”“爱”“中”“国”为A,B,C,D,画树状图如下:
( http: / / www.21cnjy.com / )
由树状图知,共有12种等可能结果,其中正面文字恰好组成“爱国”字样的结果数有2种结果,
所以其正面文字恰好组成“爱国”字样的概率.
故答案为:
【点睛】
本题主要考查了利用树状图或列表法求概率,根据题意,准确画出树状图或列出表格得到所有等可能结果是解题的关键.
5、0.3
【解析】
【分析】
由频数分布折线图知,共有10个数据,其中26℃出现3次,再根据频率的概念求解即可.
【详解】
解:由频数分布折线图知,共有10个数据,其中26℃出现3次,
所以出现气温为26℃的频率是3÷10=0.3,
故答案为:0.3.
【点睛】
本题主要考查频数(率)分布折线图,解题的关键是掌握频率的概念,根据折线图得出解题所需的数据.
三、解答题
1、 (1)
(2),,见解析
(3)
【解析】
【分析】
(1)用的频数为30÷10%计算即可;
(2)频数90÷本次调查的总人数300可求该组的频率,用的频率40%×本次调查的总人数300得出该组的频数,即可补画频数分布直方图;21教育网
(3)用360°×该组的频率30%即可.
(1)
解:∵的频数为30,占10%,
∴本次调查的学生总人数是30÷10%=300人,
故答案为:300人;
(2)
解:∵,频数90,
∴n=90÷300=0.3=30%,
∵占40%,
∴m=300×40%=120人,
( http: / / www.21cnjy.com / )
(3)
解:成绩在的百分比为30%,
成绩在的学生所对应的扇形圆心角度数360°×30%=108°.
【点睛】
本题考查频数,频率,补画频数分布直方图,求扇形统计图中圆心角度数,正确理解题意是解题关键.
2、 (1)
(2)
【解析】
【分析】
(1)直接由概率公式求解即可;
(2)画出树状图,共有9种等可能的结果 ( http: / / www.21cnjy.com ),小李经过两个十字道口后向西参观的结果有3种,向南参观的结果有2种,向北参观的结果有2种,向东参观的结果有2种,由概率公式求解即可.
(1)
小李走到十字道口A向北走的概率为;
(2)
画树状图如下:
( http: / / www.21cnjy.com / )
共有9种等可能的结果,小李经过两个十字道口后向西参观的结果有3种,向南参观的结果有2种,向北参观的结果有2种,向东参观的结果有2种,
∴向西参观的概率为.
【点睛】
本题考查的是用列表法或画树状图法求 ( http: / / www.21cnjy.com )概率.列表法或画树状图法可以不重复不遗漏的列出所有可能的结果,列表法适合于两步完成的事件,树状图法适合两步或两步以上完成的事件.注意概率=所求情况数与总情况数之比.
3、 (1)见解析
(2)9、6、0.2
【解析】
【分析】
(1)由已知数据知,晴天的有6天,多云的有18天,阴的有5天,小雪的有1天,据此补全图形即可;
(2)由已知数据知,大于等于-10℃小于-5℃的天数a=9,-10℃以下的天数b=6,其对应频率m=6÷30=0.2.21*cnjy*com
(1)
由已知数据知,晴天的有6天,多云的有18天,阴的有5天,小雪的有1天,
补全图形如下:
( http: / / www.21cnjy.com / )
(2)
由已知数据知,大于等于-10℃小于-5℃的天数a=9,
-10℃以下的天数b=6,其对应频率m=6÷30=0.2,
故答案为:9、6、0.2.
【点睛】
本题主要考查条形统计图,条形统计图是用线段长度表示数据,根据数量的多少画成长短不同的矩形直条,然后按顺序把这些直条排列起来.
4、 (1)B
(2)补全频数分布直方图见解析
(3)39,2.8
(4)选甲,理由见解析
【解析】
【分析】
(1)根据中位数的定义求出a的值,再结合扇形统计图即可确定其落在哪部分;
(2)根据所给数据可求出乙的成绩在37.5-39.5的频数为4,即可补全分布直方图;
(3)根据众数的定义即可求出b的值,根据方差的计算公式即可求出c的值.
(4)甲和乙成绩的平均值相同,判断其方差即可,方差越小,数据波动越小,成绩越稳定,甲的方差小,选甲即可.
(1)
将甲的成绩从小到大排列为:37,37,37,38,39,39,40,40,41,42
∴中位数,
根据扇形统计图可知甲成绩的中位数a落在扇形统计图的B部分.
故答案为:B.
(2)
根据所给数据可知乙的成绩在37.5-39.5的频数为4,
∴补全乙成绩的频数分布直方图如下:
( http: / / www.21cnjy.com / )
(3)
乙成绩39秒出现了3次,最多
∴.
根据方法的计算公式得:
∴.
故答案为:39,2.8.
(4)
∵,
∴甲的成绩比乙更稳定,应选甲.
【点睛】
本题考查频数分布直方图,扇形统计图,中位 ( http: / / www.21cnjy.com )数、众数、平均数以及方差,理解中位数、众数、平均数以及方差的定义,掌握中位数、众数以及方差的求法是解答本题的关键.
5、 (1)他选中《孙子算经》的概率为
(2)其中1部是《周髀算经》的概率为
【解析】
(1)
小华想从这4部数学名著中随机选择1部阅读,
则他选中《孙子算经》的概率为.
(2)
将四部名著《周髀算经》,《九章算术》,《海岛算经》,《孙子算经》分别记为A,B,C,D,
记其中1部是《周髀算经》为事件M.
用列表法列举出从4部名著中选择2部所能产生的全部结果:
第1部第2部 A B C D
A
B
C
D
由表中可以看出,所有可能的结果有12种,并且它们出现的可能性相等.
其中事件M的结果有6种,即BA,CA,DA,AB,AC,AD,
.
【点睛】
本题考查了公式法求简单概率,列 ( http: / / www.21cnjy.com )表法求概率,列表法或画树状图法可以不重复不遗漏的列出所有可能的结果数,概率=所求情况数与总情况数之比.熟练掌握求概率的方法是解题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
九年级数学下册第6章事件的概率专题攻克
考试时间:90分钟;命题人:数学教研组
考生注意:
1、本卷分第I卷(选择题)和第Ⅱ卷(非选择题)两部分,满分100分,考试时间90分钟
2、答卷前,考生务必用0.5毫米黑色签字笔将自己的姓名、班级填写在试卷规定位置上
3、答案必须写在试卷各个 ( http: / / www.21cnjy.com )题目指定区域内相应的位置,如需改动,先划掉原来的答案,然后再写上新的答案;不准使用涂改液、胶带纸、修正带,不按以上要求作答的答案无效。【出处:21教育名师】
第I卷(选择题 30分)
一、单选题(10小题,每小题3分,共计30分)
1、在一个不透明的盒子里,装有若干个除颜色不同外其余都相同的小球,如果盒子中装有4个红球且从中随机摸出一个球是红球的概率为,则盒子中小球个数为( )21*cnjy*com
A.15 B.12 C.10 D.8
2、下列说法正确的是( )
A.新冠肺炎疫情防控期间,复学学生的核酸检测适合采用抽样调查
B.程晨投篮投中的概率是0.6,说明他投10次篮球一定能中6次
C.“平分弦的直径必垂直于这条弦”是一个必然事件
D.“在一张纸上随意画两个直角三角形,这两个直角三角形相似”为随机事件
3、下列事件中是必然事件的是( )
A.任意一个三角形的外角和等于180°
B.一个数与它的相反数的和是0
C.明天会下雨
D.正月十五雪打灯
4、在一个不透明纸箱中放有除 ( http: / / www.21cnjy.com )了数字不同外,其它完全相同的2张卡片,分别标有数字1、2,从中任意摸出一张,放回搅匀后再任意摸出一张,两次摸出的数字之和为奇数的概率为( )
A. B. C. D.
5、在4张小卡片上分别写有实数0,,π,,从中随机抽取一张卡片,抽到无理数的概率是( )21cnjy.com
A. B. C. D.
6、下列各选项的事件中,是随机事件的是( )
A.向上抛的硬币会落下 B.打开电视机,正在播新闻
C.太阳从西边升起 D.长度分别为4、5、6的三条线段围成三角形
7、中国福利彩票“双色球”投注方法是每注选择 ( http: / / www.21cnjy.com )6个红色球号码(从1-33的33个数中选择)加一个蓝色球号码(从1-16中16个数中选择),若最近三期蓝色号码球的开奖结果都为奇数,则下一期蓝色球的开奖结果( )
A.还是奇数 B.一定是偶数
C.是偶数的概率大于是奇数的概率 D.是偶数的概率为
8、把一副普通扑克牌中13张黑桃牌洗匀后正面向下放在桌子上.从中随机抽取一张,抽出的牌上的数小于6的概率为( )
( http: / / www.21cnjy.com / )
A. B. C. D.
9、下列事件是必然事件的是( )
A.某种彩票中奖率为1%,则买100张这种彩票必然中奖
B.今晚努力学习,明天考试必然考出好成绩
C.从装有2个红球、3个白球的袋中随机摸出4个球,则一定会摸出红球
D.抛掷一枚普通的骰子所得的点数一定小于6
10、一个不透明的袋子中装有10个小球,其中 ( http: / / www.21cnjy.com )6个红球、4个绿球,这些小球除颜色外无其它差别.从袋子中随机摸出一个小球,则摸出的小球是红球的概率为( )
A. B. C. D.
第Ⅱ卷(非选择题 70分)
二、填空题(5小题,每小题4分,共计20分)
1、大数据分析技术为打赢疫 ( http: / / www.21cnjy.com )情防控阻击战发挥了重要作用,如图是小乐同学的健康码(绿码)示意图,用黑白打印机打印于边长为4cm的正方形区域内,为了估计图中黑色部分的总面积,在正方形区域内随机掷点,经过大量重复试验,发现点落入黑色部分的频率稳定在0.6左右,据此可以估计黑色部分的总面积约为 _____cm2.
( http: / / www.21cnjy.com / )
2、某植物种子在相同的条件下发芽试验的结果如下:
每批粒数 50 100 300 400 500 1000
发芽的频数 45 96 283 380 474 948
则该植物种子发芽的概率的估计值是______.(结果精确到0.01)
3、某博览馆有A,B两个入口和C,D,E三个出口,小明入馆游览,他从A口进E口出的概率是 _____.
4、现有四张卡片,正面分别写有汉字 ( http: / / www.21cnjy.com )“我”“爱”“中”“国”,反面是完全相同的五角星图案.现将背面朝上充分洗匀后,从中任意抽取2张,其正面文字恰好组成“爱国”字样的概率为__.
5、如图是某地2020年5月1~10日每天最高温度的折线统计图,由此图可知该地这10天中,出现气温为26℃的频率是 _____.www.21-cn-jy.com
( http: / / www.21cnjy.com / )
三、解答题(5小题,每小题10分,共计50分)
1、为了解七年级学生的期 ( http: / / www.21cnjy.com )中数学考试情况,随机抽查了部分同学的成绩(满分100分),整理并制作了不完整的统计表和统计图.请根据图表提供的信息,解答下列问题:【来源:21·世纪·教育·网】
( http: / / www.21cnjy.com / )
分数x分 频数 百分比
30 10%
90 n
m 40%
60 20%
(1)本次调查的学生总人数是______;
(2)求m、n的值,并补全频数分布直方图;
(3)若要绘制扇形统计图,求成绩在的学生所对应的扇形圆心角度数.
2、如图,是一个智慧教育产品的展销厅 ( http: / / www.21cnjy.com )的俯视示意图,小李进入展厅后,开始自由参观,每走到一个十字道口,他可能直行,也可能向左转成向右转,且这三种可能性均相同.21·世纪*教育网
( http: / / www.21cnjy.com / )
(1)求小李走进展厅的十字道口A后,向北走的概率;
(2)请用树状图或表格分析,小李到达第二个十字道口后向西方向参观的概率.
3、为了了解长春市冬季的天气变化情况,热爱气象观察的小明记录了2021年11月份30天的天气情况,具体信息如下:【来源:21cnj*y.co*m】
( http: / / www.21cnjy.com / )
日期 最高气温 最低气温 天气 日期 最高气温 最低气温 天气
11﹣01 4℃ 0℃ 多云 11﹣16 2℃ ﹣2℃ 晴
11﹣02 9℃ 3℃ 阴 11﹣17 6℃ ﹣1℃ 阴
11﹣03 12℃ 2℃ 晴 11﹣18 4℃ ﹣6℃ 多云
11﹣04 15℃ ﹣2℃ 阴 11﹣19 0℃ ﹣6℃ 多云
11﹣05 15℃ 10℃ 多云 11﹣20 0℃ ﹣7℃ 多云
11﹣06 2℃ ﹣6℃ 多云 11﹣21 ﹣4℃ ﹣9℃ 阴
11﹣07 ﹣3℃ ﹣4℃ 多云 11﹣22 ﹣8℃ ﹣12℃ 多云
11﹣08 9℃ ﹣4℃ 多云 11﹣23 ﹣8℃ ﹣15℃ 晴
11﹣09 ﹣3℃ ﹣6℃ 多云 11﹣24 ﹣7℃ ﹣14℃ 晴
11﹣10 ﹣2℃ ﹣5℃ 小雪 11﹣25 ﹣5℃ ﹣13℃ 多云
11﹣11 6℃ 2℃ 多云 11﹣26 ﹣3℃ ﹣13℃ 多云
11﹣12 ﹣1℃ ﹣7℃ 晴 11﹣27 0℃ ﹣1℃ 多云
11﹣13 4℃ ﹣6℃ 多云 11﹣28 6℃ ﹣4℃ 多云
11﹣14 12℃ 9℃ 阴 11﹣29 ﹣2℃ ﹣7℃ 多云
11﹣15 2℃ ﹣4℃ 晴 11﹣30 ﹣4℃ ﹣11℃ 多云
请你帮助小明同学把以上数据整理成统计图表.
2021年11月份长春市最低气温统计表
最低气温分组 频数 频率
10℃及10℃以上
大于等于5℃小于10℃
大于等于0℃小于5℃ 4
大于等于﹣5℃小于0℃ 9 0.3
大于等于﹣10℃小于﹣5℃ a
﹣10℃以下 b m
(1)补全条形统计图;
(2)2021年11月份长春市最低气温统计表中a= ;b= ;m= .
4、 “冰雪之约,中国之邀”, ( http: / / www.21cnjy.com )第24届冬季奥林匹克运动会即将在中国举行.某国家队计划从甲、乙两名短道速滑运动员中选派一人参赛(均取整数,单位:秒)如下:21教育名师原创作品
甲:37,41,38,40,39,37,39,42,37,40
乙:36,39,37,38,42,39,39,41,42,37
【整理数据】
甲成绩的扇形统计图(图1):
乙成绩的频数分布直方图(图2):
( http: / / www.21cnjy.com / )
【分析数据】
运动员 平均数 中位数 众数 方差
甲 39 a 37 c
乙 39 39 b 4
请根据以上信息,完成下列问题:
(1)甲成绩的中位数a落在扇形统计图的 部分(填A,B,C);
(2)请补全乙成绩的频数分布直方图;
(3)表中b= ,c= ;
【做出决策】
(4)根据甲、乙两人10次选拔比赛的成绩,你认为该国家队应选派哪位运动员参赛?并说明理由.
5、中国古代有着辉煌的数学成就,《周髀算经》,《九章算术》,《海岛算经》,《孙子算经》等是了解我国古代数学的重要文献.21世纪教育网版权所有
(1)小华想从这4部数学名著中随机选择1部阅读,求他选中《孙子算经》的概率;
(2)某中学拟从这4部数学名著中选择2 ( http: / / www.21cnjy.com )部作为“数学文化”校本课程学习内容,用列表法或树状图法求出选中的2部名著中,其中1部是《周髀算经》的概率.2·1·c·n·j·y
-参考答案-
一、单选题
1、B
【解析】
【分析】
设盒子中小球共有x个,根据概率公式得到,然后利用比例性质求出x即可.
【详解】
解:设盒子中小球共有x个,
根据题意得,
解得x=12,
经检验x=12是原方程的解,
所以盒子中小球共有12个.
故选:B.
【点睛】
本题考查了概率公式:随机事件A的概率P(A)=事件A可能出现的结果数除以所有可能出现的结果数.
2、D
【解析】
【分析】
本题需要根据调查事件的不同,选择需要全面普查还是抽样调查,根据事件本身判断事件是必然事件还是随机事件.
【详解】
解:A、对于传染疾病预防,应该对每一个人进行核酸检测,所以应选择普查的方式,选项说法错误,不符合题意;
B、程晨投篮投中的概率是0.6,说明他投10次篮球可能中6次,而非一定中6次,选项说法错误,不符合题意;
C、直径是特殊的弦,无论两条直径是否垂直都互相平分,所以这不是一个必然事件,选项说法错误,不符合题意;
D、在一张纸上随意画两个直角三角形,这两个直角三角形有可能相似,有可能不相似,所以为随机事件,选项说法正确,符合题意;
故选D.
【点睛】
本题考查统计方式的选择和必然事件,随机事件的判断,以及相似三角形的概念,根据题意选择适当的方式进行数据统计是解决本题的关键.
3、B
【解析】
【分析】
直接利用随机事件以及不可能事件、必然事件的定义分析得出答案.
【详解】
解:∵三角形的外角和等于360°,
∴任意一个三角形的外角和等于180°不是必然事件,是不可能事件,
∴A错误;
∵相反数的和为零,
∴一个数与它的相反数的和为0是必然事件,
故B正确;
∵明天会下雨是随机事件,不是必然事件,
故C错误;
∵正月十五雪打灯是随机事件,不是必然事件,
故D错误.
故选:B.
【点睛】
本题主要考查了随机事件、必然事件、不可能事件的定义,正确掌握相关定义是解题关键.
4、C
【解析】
【分析】
根据题意画出树状图求解即可.
【详解】
解:画树状图如下
( http: / / www.21cnjy.com / )
共有4种等可能的结果,两次摸出的数字之和为奇数的结果有2种
两次摸出的数字之和为奇数的概率为
故选:C.
【点睛】
此题考查了概率的问题,解题的关键是画出树状图求概率.
5、A
【解析】
【分析】
根据概率公式求解即可.
【详解】
解:∵从中随机抽取一张卡片,共有4种等可能结果,其中无理数的有1种可能结果,
∴抽到无理数的概率是,
故选:A.
【点睛】
本题主要考查概率公式,解题的关键是掌握无理数的概念和概率公式.
6、B
【解析】
【分析】
根据事件发生的可能性大小判断.
【详解】
解:A、向上抛的硬币会落下,是必然事件;
B、打开电视机,正在播新闻,是随机事件;
C、太阳从西边升起,是不可能事件;
D、长度分别为4、5、6的三条线段围成三角形,是必然事件;
故选:B.
【点睛】
本题考查的是必然事件、不可能事件、随机事件 ( http: / / www.21cnjy.com )的概念.必然事件指在一定条件下,一定发生的事件.不可能事件是指在一定条件下,一定不发生的事件,不确定事件即随机事件是指在一定条件下,可能发生也可能不发生的事件.21·cn·jy·com
7、D
【解析】
【分析】
分别求出下一期蓝色球的开奖结果是偶数的概率以及是奇数的概率,比较即可求解.
【详解】
解:由题意可知,蓝色球号码从1-16的16个数中选择,共有16种结果,1-16的16个数中偶数有8个,奇数有8个,
所以下一期蓝色球的开奖结果是偶数的概率为,
下一期蓝色球的开奖结果是奇数的概率为,
故选:D.
【点睛】
本题考查了概率公式,用到的知识点为:概率=所求情况数与总情况数之比.
8、D
【解析】
【分析】
共有13种等可能结果,小于6的有5种,利用概率公式计算即可.
【详解】
解:一副普通扑克牌中13张黑桃牌洗匀后正面向下放在桌子上.从中随机抽取一张,共有13种等可能结果,小于6的有5种,【版权所有:21教育】
抽出的牌上的数小于6的概率为,
故选:D.
【点睛】
本题考查了概率的求法,解题关键是熟记概率公式,准确列出所有可能.
9、C
【解析】
【分析】
根据必然事件是一定会发生的事件这个概念求解即可.
【详解】
解:选项A:某种彩票中奖率为1%,则买100张这种彩票必然中奖,不一定必然中奖,不合题意;
选项B:今晚努力学习,明天考试必然考出好成绩,是随机事件,不合题意;
选项C:从装有2个红球、3个白球的袋中随机摸出4个球,则一定会摸出红球,是必然事件,符合题意;
选项D:抛掷一枚普通的骰子所得的点数一定小于6,也有可能等于6,故此选项不合题意;
故选:C.
【点睛】
此题主要考查了随机事件,熟练掌握必然事件的概念是解题关键.
10、A
【解析】
【分析】
根据概率的求法,找准两点:①全部情况的总数;②符合条件的情况数目;二者的比值就是其发生的概率.
【详解】
解:∵一个不透明的袋子中装有10个小球,其中6个红球、4个绿球,
∴从袋子中随机摸出一个小球,则摸出的小球是红球的概率为.
故选:A.
【点睛】
本题考查概率的求法:如果一个事件有n种可能,而且这些事件的可能性相同,其中事件A出现m种结果,那么事件A的概率P(A)=.www-2-1-cnjy-com
二、填空题
1、9.6
【解析】
【分析】
先根据经过大量重复试验,发现点落入黑色部分的频率稳定在0.6左右,可估计点落入黑色部分的概率为0.6,再乘以正方形的面积即可得出答案.2-1-c-n-j-y
【详解】
解:∵经过大量重复试验,发现点落入黑色部分的频率稳定在0.6左右,
∴估计点落入黑色部分的概率为0.6,
∴估计黑色部分的总面积约为4×4×0.6=9.6(cm2),
故答案为:9.6.
【点睛】
本题主要考查利用频率估计概率,大 ( http: / / www.21cnjy.com )量重复实验时,事件发生的频率在某个固定位置左右摆动,并且摆动的幅度越来越小,根据这个频率稳定性定理,可以用频率的集中趋势来估计概率,这个固定的近似值就是这个事件的概率.
2、0.95
【解析】
【分析】
根据题意及频率估计概率可直接进行求解.
【详解】
解:由表格得:
当每批粒数为50时,则种子发芽的频率为;当每批粒数为100时,则种子发芽的频率为;当每批粒数为300时,则种子发芽的频率为;当每批粒数为400时,则种子发芽的频率为;当每批粒数为500时,则种子发芽的频率为;当每批粒数为1000时,则种子发芽的频率为;
∴该植物种子发芽的概率的估计值是0.95;
故答案为0.95.
【点睛】
本题主要考查利用频率估计概率,熟练掌握利用频率估计概率是解题的关键.
3、
【解析】
【分析】
画树状图,所有等可能的结果有6种,其中小明从A入口进,E出口出的有1种结果,再由概率公式求解即可.
【详解】
解:画树形图如图:
( http: / / www.21cnjy.com / )
由树形图可知,所有等可能的结果有6种,其中小明从A入口进,E出口出的有1种结果,
∴小明从A入口进,E出口出的概率为,
故答案为:.
【点睛】
本题考查的是树状图法求概率.树状 ( http: / / www.21cnjy.com )图法可以不重复不遗漏的列出所有可能的结果,适合两步或两步以上完成的事件;用到的知识点为:概率=所求情况数与总情况数之比.
4、
【解析】
【分析】
分别记“我”“爱”“中”“国”为A, ( http: / / www.21cnjy.com )B,C,D,利用树状图的方法可得所有等可能结果;再找到正面文字恰好组成“爱国”字样的结果数,利用概率公式计算可得.
【详解】
解:分别记“我”“爱”“中”“国”为A,B,C,D,画树状图如下:
( http: / / www.21cnjy.com / )
由树状图知,共有12种等可能结果,其中正面文字恰好组成“爱国”字样的结果数有2种结果,
所以其正面文字恰好组成“爱国”字样的概率.
故答案为:
【点睛】
本题主要考查了利用树状图或列表法求概率,根据题意,准确画出树状图或列出表格得到所有等可能结果是解题的关键.
5、0.3
【解析】
【分析】
由频数分布折线图知,共有10个数据,其中26℃出现3次,再根据频率的概念求解即可.
【详解】
解:由频数分布折线图知,共有10个数据,其中26℃出现3次,
所以出现气温为26℃的频率是3÷10=0.3,
故答案为:0.3.
【点睛】
本题主要考查频数(率)分布折线图,解题的关键是掌握频率的概念,根据折线图得出解题所需的数据.
三、解答题
1、 (1)
(2),,见解析
(3)
【解析】
【分析】
(1)用的频数为30÷10%计算即可;
(2)频数90÷本次调查的总人数300可求该组的频率,用的频率40%×本次调查的总人数300得出该组的频数,即可补画频数分布直方图;21教育网
(3)用360°×该组的频率30%即可.
(1)
解:∵的频数为30,占10%,
∴本次调查的学生总人数是30÷10%=300人,
故答案为:300人;
(2)
解:∵,频数90,
∴n=90÷300=0.3=30%,
∵占40%,
∴m=300×40%=120人,
( http: / / www.21cnjy.com / )
(3)
解:成绩在的百分比为30%,
成绩在的学生所对应的扇形圆心角度数360°×30%=108°.
【点睛】
本题考查频数,频率,补画频数分布直方图,求扇形统计图中圆心角度数,正确理解题意是解题关键.
2、 (1)
(2)
【解析】
【分析】
(1)直接由概率公式求解即可;
(2)画出树状图,共有9种等可能的结果 ( http: / / www.21cnjy.com ),小李经过两个十字道口后向西参观的结果有3种,向南参观的结果有2种,向北参观的结果有2种,向东参观的结果有2种,由概率公式求解即可.
(1)
小李走到十字道口A向北走的概率为;
(2)
画树状图如下:
( http: / / www.21cnjy.com / )
共有9种等可能的结果,小李经过两个十字道口后向西参观的结果有3种,向南参观的结果有2种,向北参观的结果有2种,向东参观的结果有2种,
∴向西参观的概率为.
【点睛】
本题考查的是用列表法或画树状图法求 ( http: / / www.21cnjy.com )概率.列表法或画树状图法可以不重复不遗漏的列出所有可能的结果,列表法适合于两步完成的事件,树状图法适合两步或两步以上完成的事件.注意概率=所求情况数与总情况数之比.
3、 (1)见解析
(2)9、6、0.2
【解析】
【分析】
(1)由已知数据知,晴天的有6天,多云的有18天,阴的有5天,小雪的有1天,据此补全图形即可;
(2)由已知数据知,大于等于-10℃小于-5℃的天数a=9,-10℃以下的天数b=6,其对应频率m=6÷30=0.2.21*cnjy*com
(1)
由已知数据知,晴天的有6天,多云的有18天,阴的有5天,小雪的有1天,
补全图形如下:
( http: / / www.21cnjy.com / )
(2)
由已知数据知,大于等于-10℃小于-5℃的天数a=9,
-10℃以下的天数b=6,其对应频率m=6÷30=0.2,
故答案为:9、6、0.2.
【点睛】
本题主要考查条形统计图,条形统计图是用线段长度表示数据,根据数量的多少画成长短不同的矩形直条,然后按顺序把这些直条排列起来.
4、 (1)B
(2)补全频数分布直方图见解析
(3)39,2.8
(4)选甲,理由见解析
【解析】
【分析】
(1)根据中位数的定义求出a的值,再结合扇形统计图即可确定其落在哪部分;
(2)根据所给数据可求出乙的成绩在37.5-39.5的频数为4,即可补全分布直方图;
(3)根据众数的定义即可求出b的值,根据方差的计算公式即可求出c的值.
(4)甲和乙成绩的平均值相同,判断其方差即可,方差越小,数据波动越小,成绩越稳定,甲的方差小,选甲即可.
(1)
将甲的成绩从小到大排列为:37,37,37,38,39,39,40,40,41,42
∴中位数,
根据扇形统计图可知甲成绩的中位数a落在扇形统计图的B部分.
故答案为:B.
(2)
根据所给数据可知乙的成绩在37.5-39.5的频数为4,
∴补全乙成绩的频数分布直方图如下:
( http: / / www.21cnjy.com / )
(3)
乙成绩39秒出现了3次,最多
∴.
根据方法的计算公式得:
∴.
故答案为:39,2.8.
(4)
∵,
∴甲的成绩比乙更稳定,应选甲.
【点睛】
本题考查频数分布直方图,扇形统计图,中位 ( http: / / www.21cnjy.com )数、众数、平均数以及方差,理解中位数、众数、平均数以及方差的定义,掌握中位数、众数以及方差的求法是解答本题的关键.
5、 (1)他选中《孙子算经》的概率为
(2)其中1部是《周髀算经》的概率为
【解析】
(1)
小华想从这4部数学名著中随机选择1部阅读,
则他选中《孙子算经》的概率为.
(2)
将四部名著《周髀算经》,《九章算术》,《海岛算经》,《孙子算经》分别记为A,B,C,D,
记其中1部是《周髀算经》为事件M.
用列表法列举出从4部名著中选择2部所能产生的全部结果:
第1部第2部 A B C D
A
B
C
D
由表中可以看出,所有可能的结果有12种,并且它们出现的可能性相等.
其中事件M的结果有6种,即BA,CA,DA,AB,AC,AD,
.
【点睛】
本题考查了公式法求简单概率,列 ( http: / / www.21cnjy.com )表法求概率,列表法或画树状图法可以不重复不遗漏的列出所有可能的结果数,概率=所求情况数与总情况数之比.熟练掌握求概率的方法是解题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
