第8章 角专项练习试题(含解析)

中小学教育资源及组卷应用平台
青岛版七年级数学下册第8章角专项练习
考试时间：90分钟；命题人：数学教研组
考生注意：
1、本卷分第I卷（选择题）和第Ⅱ卷（非选择题）两部分，满分100分，考试时间90分钟
2、答卷前，考生务必用0.5毫米黑色签字笔将自己的姓名、班级填写在试卷规定位置上
3、答案必须写在试卷各个题目指定 ( http: / / www.21cnjy.com )区域内相应的位置，如需改动，先划掉原来的答案，然后再写上新的答案；不准使用涂改液、胶带纸、修正带，不按以上要求作答的答案无效。21*cnjy*com
第I卷（选择题 30分）
一、单选题（10小题，每小题3分，共计30分）
1、如图，O是直线AB上一点，则图中互为补角的角共有（ ）
( http: / / www.21cnjy.com / )
A．1对 B．2对 C．3对 D．4对
2、如图，于O，直线CD经过O，，则的度数是（ ）
( http: / / www.21cnjy.com / )
A． B． C． D．
3、如图，∠AOB，以OA为边作∠AOC，使∠BOC=∠AOB，则下列结论成立的是（ ）
( http: / / www.21cnjy.com / )
A． B．
C．或 D．或
4、若的补角是，则的余角是（ ）
A． B． C． D．
5、如图，直线AB和CD相交于点O，下列选项中与∠AOC互为邻补角的是（　　）
( http: / / www.21cnjy.com / )
A．∠BOC B．∠BOD C．∠DOE D．∠AOE
6、如图，将一块三角板60°角的顶点与另一块三角板的直角顶点重合，，的大小是（ ）
( http: / / www.21cnjy.com / )
A． B． C． D．
7、钟表上1时30分时，时针与分针所成的角是（ ）
A． B． C． D．以上答案都不对
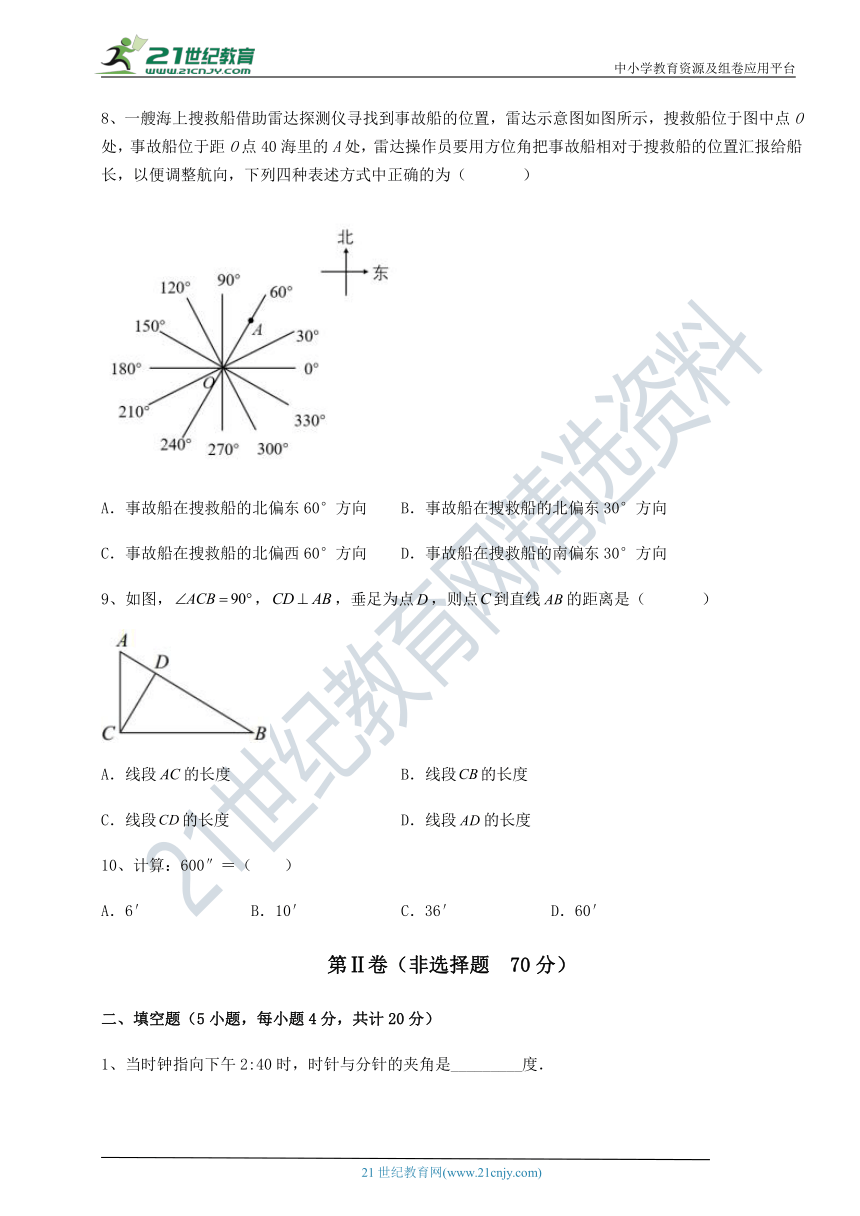
8、一艘海上搜救船借助雷达探测仪 ( http: / / www.21cnjy.com )寻找到事故船的位置，雷达示意图如图所示，搜救船位于图中点O处，事故船位于距O点40海里的A处，雷达操作员要用方位角把事故船相对于搜救船的位置汇报给船长，以便调整航向，下列四种表述方式中正确的为（ ）【出处：21教育名师】
( http: / / www.21cnjy.com / )
A．事故船在搜救船的北偏东60°方向 B．事故船在搜救船的北偏东30°方向
C．事故船在搜救船的北偏西60°方向 D．事故船在搜救船的南偏东30°方向
9、如图，，，垂足为点，则点到直线的距离是（ ）
( http: / / www.21cnjy.com / )
A．线段的长度 B．线段的长度
C．线段的长度 D．线段的长度
10、计算：600″＝（　　）
A．6′ B．10′ C．36′ D．60′
第Ⅱ卷（非选择题 70分）
二、填空题（5小题，每小题4分，共计20分）
1、当时钟指向下午2:40时，时针与分针的夹角是_________度．
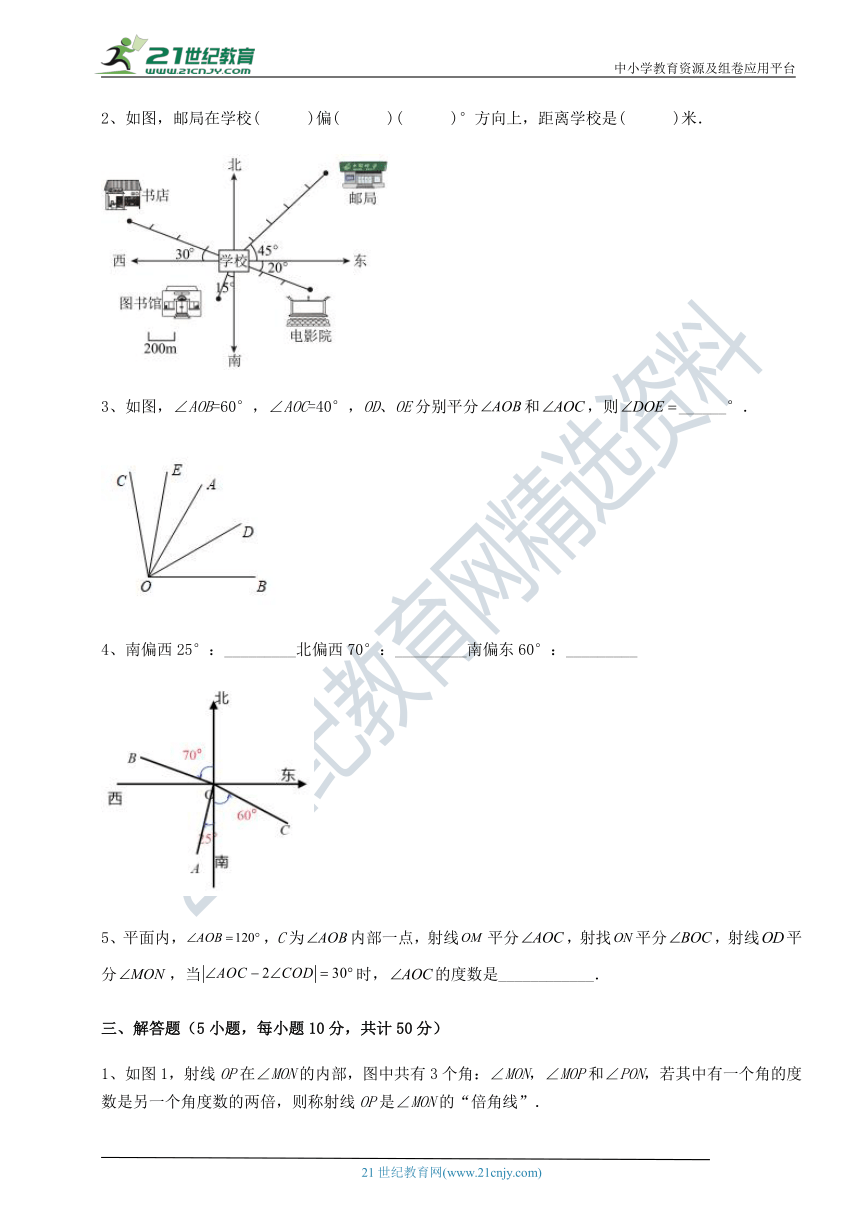
2、如图，邮局在学校( )偏( )( )°方向上，距离学校是( )米．
( http: / / www.21cnjy.com / )
3、如图，∠AOB=60°，∠AOC=40°，OD、OE分别平分和，则______°．
( http: / / www.21cnjy.com / )
4、南偏西25°：_________北偏西70°：_________南偏东60°：_________【版权所有：21教育】
( http: / / www.21cnjy.com / )
5、平面内，，C为内部一点，射线平分，射找平分，射线平分，当时，的度数是____________．21教育名师原创作品
三、解答题（5小题，每小题10分，共计50分）
1、如图1，射线OP在∠MON的内部，图中共 ( http: / / www.21cnjy.com )有3个角：∠MON，∠MOP和∠PON，若其中有一个角的度数是另一个角度数的两倍，则称射线OP是∠MON的“倍角线”．
( http: / / www.21cnjy.com / )
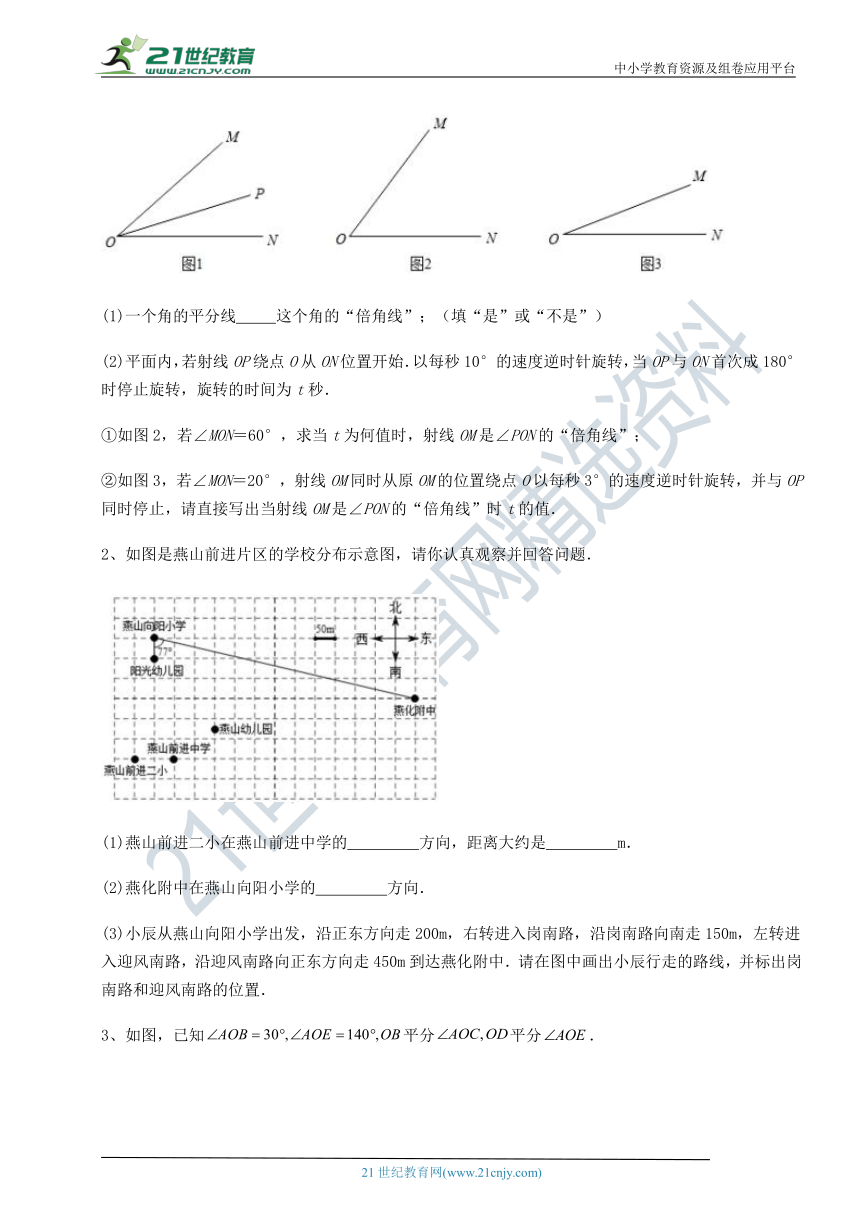
(1)一个角的平分线　 　这个角的“倍角线”；（填“是”或“不是”）
(2)平面内，若射线OP绕点O从ON位置开始．以每秒10°的速度逆时针旋转，当OP与ON首次成180°时停止旋转，旋转的时间为t秒．
①如图2，若∠MON＝60°，求当t为何值时，射线OM是∠PON的“倍角线”；
②如图3，若∠MON＝20° ( http: / / www.21cnjy.com )，射线OM同时从原OM的位置绕点O以每秒3°的速度逆时针旋转，并与OP同时停止，请直接写出当射线OM是∠PON的“倍角线”时t的值．
2、如图是燕山前进片区的学校分布示意图，请你认真观察并回答问题．
( http: / / www.21cnjy.com / )
(1)燕山前进二小在燕山前进中学的 方向，距离大约是 m．
(2)燕化附中在燕山向阳小学的 方向．
(3)小辰从燕山向阳小学出发，沿正东方向走 ( http: / / www.21cnjy.com )200m，右转进入岗南路，沿岗南路向南走150m，左转进入迎风南路，沿迎风南路向正东方向走450m到达燕化附中．请在图中画出小辰行走的路线，并标出岗南路和迎风南路的位置．
3、如图，已知平分平分．
( http: / / www.21cnjy.com / )
(1)求的度数．
(2)求的度数．
4、如图（1），直线、相交于点，直角三角板边落在射线上，将三角板绕点逆时针旋转180°．
( http: / / www.21cnjy.com / )
(1)如图（2），设，当平分时，求（用表示）
(2)若，
①如图（3），将三角板旋转，使落在内部，试确定与的数量关系，并说明理由．
②若三角板从初始位置开始，每秒旋转5°，旋转时间为，当与互余时，求的值．
5、如图，点A、O、B在同一条直线上，射线OD平分∠AOC，且∠DOE＝90°．求证：OE平分∠BOC．
( http: / / www.21cnjy.com / )
-参考答案-
一、单选题
1、B
【解析】
【分析】
根据补角定义解答．
【详解】
解：互为补角的角有：∠AOC与∠BOC，∠AOD与∠BOD，共2对，
故选：B．
【点睛】
此题考查了补角的定义：和为180度的两个角互为补角，熟记定义是解题的关键．
2、B
【解析】
【分析】
由OA⊥OB，得出∠AOB=90°，再根据∠AOD=35°，由余角的定义可得出∠BOD，再根据补角的定义可得出∠BOC的度数．21cnjy.com
【详解】
解：∵OA⊥OB，
∴∠AOB=90°，
∵∠AOD=35°，
∴∠BOD=90°-35°=55°，
∴∠BOC=180-55°=125°，
故选B．
【点睛】
本题考查了垂线的定义，平角的定义，关键是利用90°和180°的数据进行计算．
3、D
【解析】
【分析】
分OC在∠AOB内部和OC在∠AOB外部两种情况讨论，画出图形即可得出结论．
【详解】
解：当OC在∠AOB内部时，
( http: / / www.21cnjy.com / )
∵∠BOC=∠AOB，即∠AOB=2∠BOC，
∴∠AOC=∠BOC；
当OC在∠AOB外部时，
( http: / / www.21cnjy.com / )
∵∠BOC=∠AOB，即∠AOB=2∠BOC，
∴∠AOC=3∠BOC；
综上，∠AOC=∠BOC或∠AOC=3∠BOC；
故选：D．
【点睛】
本题考查了角平分线的定义，熟练掌握角平分线的定义，数形结合解题是关键．
4、B
【解析】
【分析】
直接利用一个角的余角和补角差值为90°，进而得出答案．
【详解】
解：∵∠α的补角等于130°，
∴∠α的余角等于：130°-90°=40°．
故选：B．
【点睛】
本题主要考查了余角和补角，正确得出余角和补角的关系是解题关键．
5、A
【解析】
【详解】
解：图中与互为邻补角的是和，
故选：A．
【点睛】
本题考查了邻补角，熟练掌握邻补角的定义（两个角有一条公共边，且它们的另一边互为反向延长线，具有这种关系的两个角互为邻补角）是解题关键．2-1-c-n-j-y
6、B
【解析】
【分析】
根据∠BAC=60°，∠1=27°20′，求出∠EAC的度数，再根据∠2=90°-∠EAC，即可求出∠2的度数．
【详解】
解：∵∠BAC=60°，∠1=27°20′，
∴∠EAC=32°40′，
∵∠EAD=90°，
∴∠2=90°-∠EAC=90°-32°40′=57°20′；
故选：B．
【点睛】
本题主要考查了与三角板有关的角度计算，解题的关键是能够正确求出∠EAC的度数．
7、C
【解析】
【分析】
钟表上12个大格把一个周角12等 ( http: / / www.21cnjy.com )分，每个大格30°，1点30分时针与分针之间共4.5个大格，故时针与分针所成的角是4.5×30°＝135°．21教育网
【详解】
解：∵1点30分，时针指向1和2的中间，分针指向6，中间相差4格半，
钟表12个数字，每相邻两个数字之间的夹角为30°，
∴1点30分分针与时针的夹角是4.5×30°＝135°．
故选：C．
【点睛】
本题考查钟表时针与分针的夹角．在钟表问题中，常利用时针与分针转动的度数关系：分针每转动1°时针转动（）°，并且利用起点时间时针和分针的位置关系建立角的图形．21*cnjy*com
8、B
【解析】
【分析】
根据点的位置确定应该有方向以及距离，进而利用方位角转化为方向角得出即可．
【详解】
A. 事故船在搜救船的北偏东60°方向，是从0°算起30°方向不是事故船方向，故选项A不正确；
B. 事故船在搜救船的北偏东30°方向，是从0°算起60°方向是事故船的方向，故选项B正确；
C. 事故船在搜救船的北偏西60°方向，是从0°算起150°方向，不是事故船出现的方向，故选项C不正确； 【来源：21cnj*y.co*m】
D. 事故船在搜救船的南偏东30°方向，是从0°算起300°方向，不是事故船的方向，故选项D不正确．
故选B．
【点睛】
本题考查了方位角的定义，确定方位角的两个要素：一是方向；二是角度，掌握理解定义是解题关键．
9、C
【解析】
【分析】
直线外一点到直线的垂线段的长度，叫做点到直线的距离，根据点到直线的距离的定义解答即可．
【详解】
∵于D，
∴点到直线的距离是指线段的长度．
故选：C．
【点睛】
本题考查了点到直线的距离的定义，点到直线的距离是一个长度，而不是一个图形，也就是垂线段的长度，而不是垂线段．2·1·c·n·j·y
10、B
【解析】
【分析】
根据，计算即可得．
【详解】
解：，
故选：B
【点睛】
题目主要考查角度各单位间的换算，熟练掌握角度单位之间的进率是解题关键．
二、填空题
1、
【解析】
【分析】
如图，钟面被等分成12份，每一份对应的角为先求解 根据时针每分钟转，再求解 从而可得答案.
【详解】
解：如图，时钟指向下午2:40时，
( http: / / www.21cnjy.com / )
钟面被等分成12份，每一份对应的角为
时针每分钟转
故答案为：
【点睛】
本题考查的是钟面角的计算，角的和差关系，掌握“钟面被等分成12份，每一份对应的角为时针每分钟转”是解本题的关键.21世纪教育网版权所有
2、 北
东 45 1000
【解析】
【分析】
图上距离1厘米表示实际距离200米，于是即可求出它们之间的实际距离，再根据它们之间的方向关系，即可进行解答．www.21-cn-jy.com
【详解】
解：邮局在学校北偏东45°的方向上，距离学校 1000米．
故答案为：北，东，45，1000．
【点睛】
此题主要考查了方位角，以及线段比例尺的意义的理解和灵活应用．
3、50
【解析】
【分析】
由OD、OE分别平分∠AOB、∠AOC．可得出∠AOE=∠EOC=∠AOC，∠DOB=∠AOD=∠AOB，进一步求出∠DOE即可．www-2-1-cnjy-com
【详解】
解：∵OD、OE分别平分∠AOB、∠AOC，∠AOB=60°，∠AOC=40°，
∴∠AOE=∠EOC=∠AOC=20°，∠DOB=∠AOD=∠AOB=30°，
∴∠DOE=∠AOD+∠AOE=30°+20°=50°；
故答案为：50．
【点睛】
本题考查了角平分线的意义，角的和与差，熟记各图形的性质并准确识图是解题的关键．
4、 射线OA 射线OB 射线OC
【解析】
略
5、45°或15°
【解析】
【分析】
根据角平分线的定义和角的运算，分射线OD在∠AOC外部和射线OD在∠AOC内部求解即可．
【详解】
解：∵射线平分，射找平分，
∴∠MOC= ∠AOC，∠NOC= ∠BOC，
∴∠MON=∠MOC+∠NOC=∠AOC+∠BOC=∠AOB=60°，
∵射线平分，
∴∠MOD= ∠MON=30°，
若射线OD在∠AOC外部时，如图1，
则∠COD=∠MOD－∠MOC=30°－∠AOC，
即2∠COD=60°－∠AOC，
∵，
∴，
解得：∠AOC=45°或15°；
若射线OD在∠AOC内部时，如图2，
则∠COD=∠MOC－∠MOD=∠AOC－30°，
∴2∠COD=∠AOC－60°，即∠AOC－2∠COD=60°，不满足，
综上，∠AOC=45°或15°，
故答案为：45°或15°．
( http: / / www.21cnjy.com / ) ( http: / / www.21cnjy.com / )
【点睛】
本题考查角平分线的定义、角的运算，熟练掌握角平分线的定义和角的有关计算，利用分类讨论思想求解是解答的关键．21·cn·jy·com
三、解答题
1、 (1)是
(2)①9或12或18；②或10
【解析】
【分析】
（1）根据角平分线的定义、角的“倍角线”的定义解答；
（2）分∠MON＝2∠MOP、∠PON＝2∠MON、∠MOP＝2∠MON三种情况，根据角的“倍角线”的定义解答；
（3）分三种情况：当∠MON＝2∠MOP时，当∠PON＝2∠MON时，当∠MOP＝2∠MON时，即可求解．
(1)
解：如果OP平分∠MON，
那么∠MON＝2∠MOP，
∴一个角的平分线是这个角的“倍角线”，
故答案为：是；
(2)
解：①由题意得：∠NOP＝（10t）°，
当∠MON＝2∠MOP时，10t＝60+×60，
解得：t＝9；
当∠PON＝2∠MON时，10t＝2×60，
解得：t＝12；
当∠MOP＝2∠MON时，10t＝60+2×60，
解得：t＝18；
综上所述：当t为9或12或18时，射线OM是∠PON的“倍角线”；
②由题意得：∠NOP＝（10t）°，∠MON＝（20+3t）°，
当∠MON＝2∠MOP时，20+3t＝2[10t﹣（20+3t）]，
解得：t＝；
当∠PON＝2∠MON时，10t＝2×（20+3t），
解得：t＝10；
当∠MOP＝2∠MON时，10t﹣（20+3t）＝2×（20+3t），
解得：t＝60（不合题意）；
综上所述：当t为或10时，射线OM是∠PON的“倍角线”．
【点睛】
本题主要考查了有关角平分线的计算，角的数量关系，理解新定义，利用分类讨论思想解答是解题的关键．
2、 (1)正西，100
(2)南偏东77°
(3)见解析
【解析】
【分析】
（1）根据图中位置解决问题即可．
（2）根据图中位置解决问题即可．
（3）根据题意画出路线即可．
(1)
燕山前进二小在燕山前进中学的正西方向，距离大约是．
故答案为：正西，100．
(2)
燕化附中在燕山向阳小学的南偏东方向
故答案为：南偏东．
(3)
小辰行走的路线如图：
( http: / / www.21cnjy.com / )
【点睛】
本题考查作图应用与设计，方向角等知识，解题的关键是熟练掌握基本知识．
3、 (1)60°
(2)10°
【解析】
【分析】
（1）根据角平分线的定义得∠AOC ＝2∠AOB，即可求解；
（2）先求出∠COE的度数，再求出∠DOE的度数，最后根据∠COD＝∠COE－∠DOE计算即可.
(1)
∠AOB ＝，OB平分∠AOC
∠AOC ＝2∠AOB＝2＝
(2)
∠AOE＝，∠AOC ＝
∠COE＝∠AOE－∠AOC＝－＝
又OD平分∠AOE
∠DOE＝∠AOE＝＝70°
∠COD＝∠COE－∠DOE＝－＝
【点睛】
本题主要考查角平分线的定义，掌握角平分线把已知角分成两个相等的角是解题的关键．
4、 (1)
(2)①，理由见解析；②4秒或22秒
【解析】
【分析】
（1）利用角的和差关系求解 再利用角平分线的含义求解即可；
（2）①设，再利用角的和差关系依次求解， ，， 从而可得答案；②由题意得：与重合是第18秒，与重合是第8秒，停止是36秒．再分三种情况讨论：如图，当时 ，，如图，当时 ，，如图，当时，，，再利用互余列方程解方程即可.【来源：21·世纪·教育·网】
(1)
解：
∵平分
∴
(2)
解：①设，则，
∴
∴，
∴
②由题意得：与重合是第18秒，与重合是第8秒，停止是36秒．
如图，当时 ，，
( http: / / www.21cnjy.com / )
则，
∴
如图，当时 ，，
( http: / / www.21cnjy.com / )
则，方程无解，不成立
如图，当时，，，
( http: / / www.21cnjy.com / )
则，
∴
综上所述秒或22秒
【点睛】
本题考查的是角的和差运算，角平分线的定义，角的动态定义的理解，互为余角的含义，清晰的分类讨论是解本题的关键.21·世纪*教育网
5、见解析
【解析】
【分析】
利用同角的余角相等进行证明即可．
【详解】
证明：∵点A、O、B在同一条直线上，∠DOE＝90°，
∴∠DOC+∠COE＝90°，∠AOD+∠BOE＝90°，
∵OD平分∠AOC，
∴∠AOD＝∠DOC，
∴∠AOD+∠COE＝90°，
∵∠AOD+∠BOE＝90°，
∴∠COE＝∠BOE，
∴OE平分∠BOC．
【点睛】
本题考查角平分线的定义，熟练掌握角平分线的定义，结合同角的余角相等是解题的关键．
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 （共 2 页）
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)