第9章 平行线章节练习试题(含解析)

中小学教育资源及组卷应用平台
青岛版七年级数学下册第9章平行线章节练习
考试时间：90分钟；命题人：数学教研组
考生注意：
1、本卷分第I卷（选择题）和第Ⅱ卷（非选择题）两部分，满分100分，考试时间90分钟
2、答卷前，考生务必用0.5毫米黑色签字笔将自己的姓名、班级填写在试卷规定位置上
3、答案必须写在试卷各个题目指定区域内 ( http: / / www.21cnjy.com )相应的位置，如需改动，先划掉原来的答案，然后再写上新的答案；不准使用涂改液、胶带纸、修正带，不按以上要求作答的答案无效。21世纪教育网版权所有
第I卷（选择题 30分）
一、单选题（10小题，每小题3分，共计30分）
1、如图，AF是∠BAC的平分线， DF∥AC，若∠1＝25°，则∠BDF的度数为（　　）
( http: / / www.21cnjy.com / )
A．25° B．50° C．75° D．100°
2、下列命题中，为真命题的是（ ）
A．若，则 B．若，则
C．同位角相等 D．对顶角相等
3、如图，点，，，在同一条直线上，，，则的度数是（ ）
( http: / / www.21cnjy.com / )
A． B． C． D．
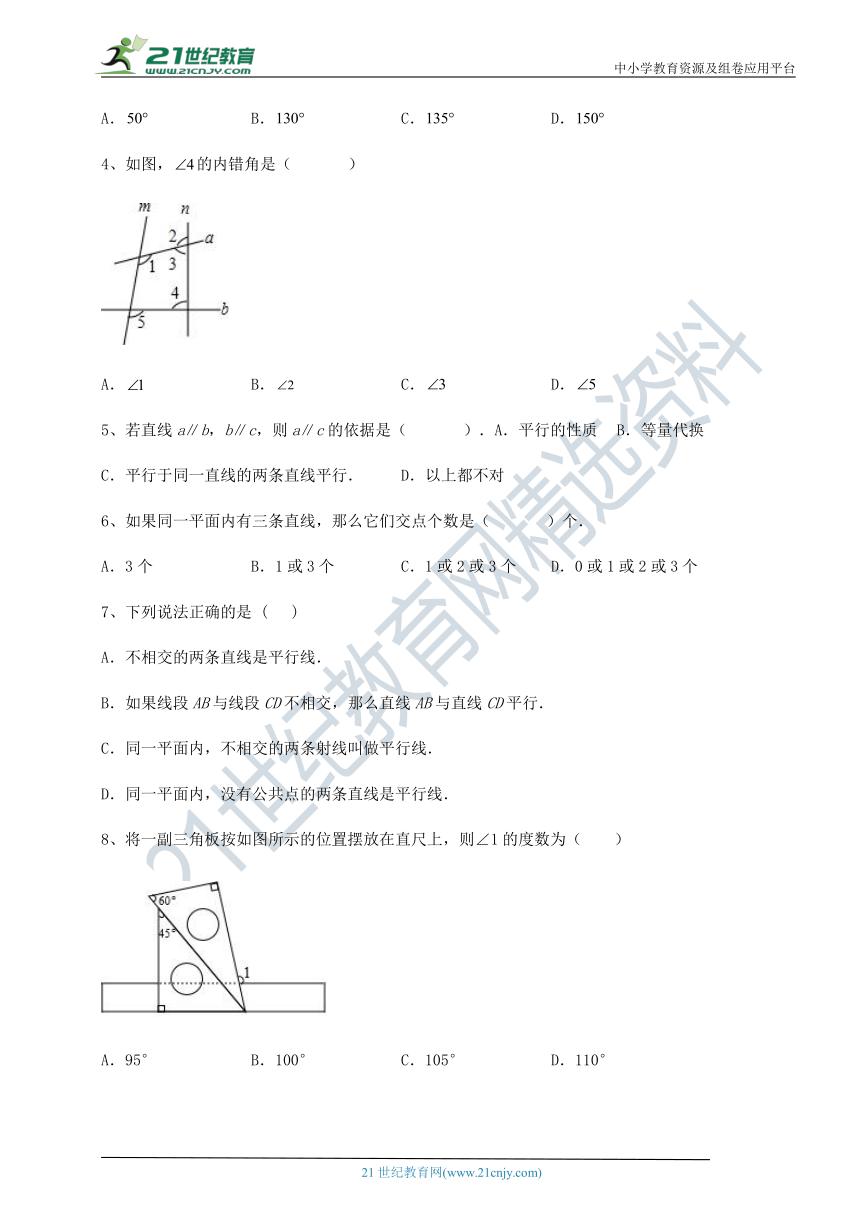
4、如图，的内错角是（ ）
( http: / / www.21cnjy.com / )
A． B． C． D．
5、若直线a∥b，b∥c，则a∥c的依据是（ ）．A．平行的性质 B．等量代换
C．平行于同一直线的两条直线平行． D．以上都不对
6、如果同一平面内有三条直线，那么它们交点个数是（ ）个．
A．3个 B．1或3个 C．1或2或3个 D．0或1或2或3个
7、下列说法正确的是 ( )
A．不相交的两条直线是平行线．
B．如果线段AB与线段CD不相交，那么直线AB与直线CD平行．
C．同一平面内，不相交的两条射线叫做平行线．
D．同一平面内，没有公共点的两条直线是平行线．
8、将一副三角板按如图所示的位置摆放在直尺上，则∠1的度数为（　　）
( http: / / www.21cnjy.com / )
A．95° B．100° C．105° D．110°
9、一个学员在广场上驾驶汽车，两次拐弯后，行驶的方向与原来的方向相同，这两次拐弯的角度可能是（ ）21教育网
A．第一次向右拐 50° ，第二次向左拐130° B．第一次向右拐 50° ，第二次向右拐130°
C．第一次向左拐 50° ，第二次向左拐130° D．第一次向左拐 30° ，第二次向右拐 30°
10、下列说法正确的有（ ）
①两点之间的所有连线中，线段最短；
②相等的角叫对顶角；
③过一点有且只有一条直线与已知直线平行；
④过一点有且只有一条直线与已知直线垂直；
⑤两点之间的距离是两点间的线段；
⑥在同一平面内的两直线位置关系只有两种：平行或相交．
A．1个 B．2个 C．3个 D．4个
第Ⅱ卷（非选择题 70分）
二、填空题（5小题，每小题4分，共计20分）
1、如图，将一块三角板的直角顶点放在直尺的一边上，若∠1＝34°，则∠2＝_____°．
( http: / / www.21cnjy.com / )
2、如图，AB∥CD∥EF，若∠ABC＝125°，∠CEF＝105°，则∠BCE的度数为 _____．
( http: / / www.21cnjy.com / )
3、点A在点B的北偏东80°方向上，点C在射线BA与正北方向夹角的角平分线上，那么点C位于点A__处．21cnjy.com
4、两条射线或线段平行，是指_______________________．
5、两条直线相交，可以构成四个角，若在图中再添加一条直线，即直线EF被第三条直线CD所截，构成了_____个角，简称“______”．21·cn·jy·com
( http: / / www.21cnjy.com / )
同位角：
图中∠1与∠5，这两个角分别在直线AB，CD的同一方（上方），并且都在直线EF的同侧（右侧），具有这种位置关系的一对角叫做______．【来源：21·世纪·教育·网】
图中还有同位角：______．
内错角：
∠3与∠5，这两个角分别在直线 ( http: / / www.21cnjy.com )AB，CD之间，并且分别在直线EF两侧，（∠3在直线EF左侧，∠5在直线EF右侧），具有这种位置关系的一对角叫做______．21·世纪*教育网
图中还有内错角：______．
同旁内角：
∠3与∠6，这两个角分别在直线AB，CD之间，但它们在直线EF的同一旁（左侧），具有这种位置关系的一对角叫做______．21*cnjy*com
图中还有同旁内角：______ ．
三、解答题（5小题，每小题10分，共计50分）
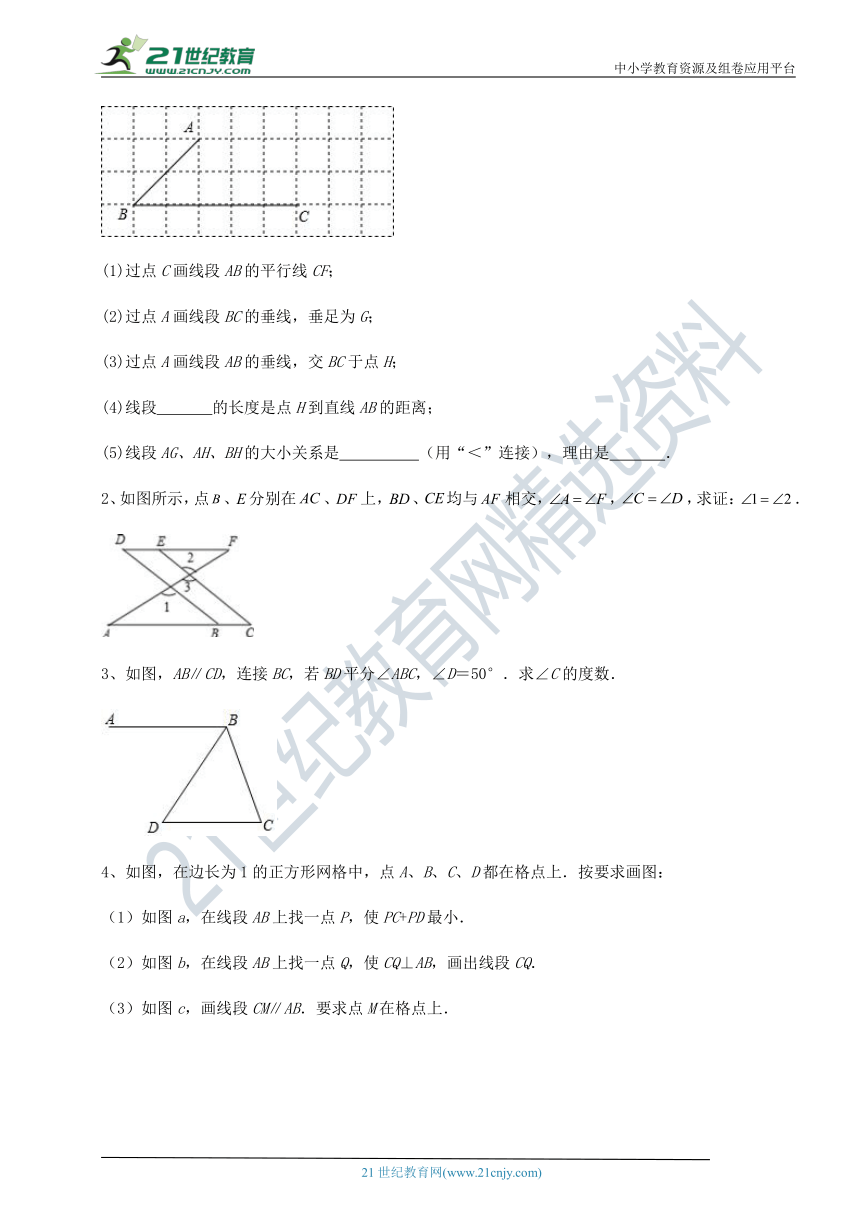
1、如图，所有小正方形的边长都为1个单位，A、B、C均在格点上．
( http: / / www.21cnjy.com / )
(1)过点C画线段AB的平行线CF；
(2)过点A画线段BC的垂线，垂足为G；
(3)过点A画线段AB的垂线，交BC于点H；
(4)线段 的长度是点H到直线AB的距离；
(5)线段AG、AH、BH的大小关系是 （用“＜”连接），理由是 ．
2、如图所示，点、分别在、上，、均与相交，，，求证：．
( http: / / www.21cnjy.com / )
3、如图，AB∥CD，连接BC，若BD平分∠ABC，∠D＝50°．求∠C的度数．
( http: / / www.21cnjy.com / )
4、如图，在边长为1的正方形网格中，点A、B、C、D都在格点上．按要求画图：
（1）如图a，在线段AB上找一点P，使PC+PD最小．
（2）如图b，在线段AB上找一点Q，使CQ⊥AB，画出线段CQ．
（3）如图c，画线段CM∥AB．要求点M在格点上．
( http: / / www.21cnjy.com / )
5、问题情境：如图1，，，，求的度数．
( http: / / www.21cnjy.com / )　　
小明的思路是：如图2，过作，通过平行线性质，可得______．
问题迁移：如图3，，点在射线上运动，，．
（1）当点在、两点之间运动时，、、之间有何数量关系？请说明理由．
（2）如果点在、两点外侧运动时（点与点、、三点不重合），请你直接写出、、之间有何数量关系．www.21-cn-jy.com
-参考答案-
一、单选题
1、B
【解析】
【分析】
根据两直线平行，同位角相等，可得∠FAC＝∠1，再根据角平分线的定义可求得∠BAC的度数，再利用平行线的性质可求解．【版权所有：21教育】
【详解】
解：∵DF∥AC，
∴∠FAC＝∠1＝25°，
∵AF是∠BAC的平分线，
∴∠BAF＝∠FAC＝25°，
∴∠BAC＝50°，
∵DF∥AC，
∴∠BDF＝∠BAC＝50°．
故选：B
【点睛】
本题主要考查了平行线的性质，角平分线的定义，熟练掌握两直线平行，同位角相等是解题的关键．
2、D
【解析】
【分析】
利用互为相反数的两个数的平方也相等，有理数的大小比较，同位角和对顶角的概念性质进行分析判断即可．
【详解】
解：A、若，则或，故A错误．
B、当时，有，故B错误．
C、两直线平行，同位角相等，故C错误．
D、对顶角相等，D正确．
故选：D ．
【点睛】
本题主要是考查了平方、绝对值的比较大小、同位角和对顶角的性质，熟练掌握相关概念及性质，是解决本题的关键．21教育名师原创作品
3、B
【解析】
【分析】
根据推出，求出的度数即可求出答案．
【详解】
，
∴，
，
，
．
故选：．
【点睛】
此题考查了平行线的判定及性质，熟记平行线的判定定理：内错角相等两直线平行是解题的关键．
4、D
【解析】
【分析】
根据内错角是在截线两旁，被截线之内的两角，内错角的边构成” “形作答．
【详解】
解：如图，的内错角是，∠4的同旁内角是∠3，∠4的同位角是∠2，∠4与∠1不具有特殊位置关系．
故选：．
【点睛】
本题考查了内错角的定义，正确记忆内错角的定义是解决本题的关键．
5、C
【解析】
【分析】
根据平行公理的推论进行判断即可．
【详解】
解：直线a∥b，b∥c，则a∥c的依据是平行于同一直线的两条直线平行，
故选：C．
【点睛】
本题考查了平行公理的推论，解题关键是明确平行于同一直线的两条直线平行．
6、D
【解析】
【分析】
根据三条直线是否有平行线分类讨论即可．
【详解】
解：当三条直线平行时，交点个数为0；
当三条直线相交于1点时，交点个数为1；
当三条直线中，有两条平行，另一条分别与他们相交时，交点个数为2；
当三条直线互相不平行时，且交点不重合时，交点个数为3；
所以，它们的交点个数有4种情形．
故选：D．
【点睛】
本题考查多条直线交点问题，解题关键是根据三条直线中是否有平行线和是否交于一点进行分类讨论．
7、D
【解析】
【分析】
根据平行线的定义逐项分析即可．
【详解】
A、同一平面内不相交的两条直线是平行线，故此说法错误；
B、两条线段不相交也可以不平行，故此说法错误；
C、同一平面内，不相交的两条射线可以平行，也可以既不平行也不相交，故此说法错误；
D、同一平面内，没有公共点的两条直线是平行线，此说法正确，
故选D．
【点睛】
本题考查了平行线的定义，理解此定义是关键，属于概念基础题．
8、C
【解析】
【分析】
根据平角的定义和平行线的性质即可得到答案．
【详解】
如图：
∵∠2＝180°﹣30°﹣45°＝105°，
∵AB∥CD，
∴∠1＝∠2＝105°，
故选：C．
( http: / / www.21cnjy.com / )
【点睛】
本题考查了平行线的性质，牢记“两直线平行，同位角相等”是解题的关键．
9、D
【解析】
【分析】
根据题意可得两直线平行则同位角相等，据此分析判断即可．
【详解】
解：∵两次拐弯后，按原来的相反方向前进，
∴两次拐弯的方向相同，形成的角是同位角，
故答案为：D
【点睛】
本题考查了平行线的性质，掌握平行线的性质是解题的关键．
10、B
【解析】
【分析】
根据所学的相关知识,逐一判断即可．
【详解】
解：①两点之间的所有连线中，线段最短，故①说法正确．
②相等的角不一定是对顶角，故②说法错误．
③经过直线外一点有且只有一条直线与已知直线平行，故③说法错误．
④同一平面内，过一点有且只有一条直线与已知直线垂直，故④说法错误．
⑤两点之间的距离是两点间的线段的长度，故⑤说法错误．
⑥在同一平面内，两不重合的直线的位置关系只有两种：相交和平行，故⑥说法正确．
综上所述，正确的结论有2个．
故选：．
【点睛】
本题主要考查对平行线的定义，两点间的距离，相交线等知识点的理解和掌握，能熟练地运用性质进行说理是解此题的关键．2·1·c·n·j·y
二、填空题
1、56
【解析】
【分析】
先根据余角的定义求出∠3的度数，再由平行线的性质即可得出结论．
【详解】
解：∵∠1＝34°，
∴∠3＝90°﹣34°＝56°．
∵直尺的两边互相平行，
∴∠2＝∠3＝56°．
故答案为：56．
( http: / / www.21cnjy.com / )
【点睛】
本题考查平行线的性质、直角三角形的性质等知识，解题的关键是灵活运用所学知识解决问题，属于中考常考题型．2-1-c-n-j-y
2、50°##50度
【解析】
【分析】
由AB∥CD∥EF，得到∠BCD=∠AB ( http: / / www.21cnjy.com )C=125°，∠CEF+∠ECD=180°，则∠ECD=180°-∠CEF=75°，由此即可得到答案．
【详解】
解：∵AB∥CD∥EF，
∴∠BCD=∠ABC=125°，∠CEF+∠ECD=180°，
∴∠ECD=180°-∠CEF=75°，
∴∠BCE=∠BCD-∠ECD=50°，
故答案为：50°．
【点睛】
本题主要考查了平行线的性质，熟知平行线的性质是解题的关键．
3、北偏东40°
【解析】
【分析】
先根据题意画出图形，可得∠DBF=8 ( http: / / www.21cnjy.com )0°，DB//EA，由平行线的性质可得∠EAF=∠DBF=80°，结合角平分线的定义可求解∠EAC=40°，进而可求解答案．
【详解】
解：如图，∠DBF=80°，DB//EA，
( http: / / www.21cnjy.com / )
∴∠EAF=∠DBF=80°，
∵AC平分∠EAF，
∴∠EAC=40°，
∴点C位于点A北偏东40°，
故答案为：北偏东40°．
【点睛】
本题主要考查方向角，角平分线的定义，平行线的性质，根据题意画出图形是解题的关键．
4、射线或线段所在的直线平行
【解析】
【分析】
根据直线、线段、射线的关系以及平行线的知识进行解答．
【详解】
解：两条射线或线段平行，是指：射线或线段所在的直线平行，
故答案为：射线或线段所在的直线平行．
【点睛】
本题考查了直线、线段、射线以及平行线的问题，本题是对基础知识的考查，记忆时一定要注意公理或定义、性质成立的前提条件．21*cnjy*com
5、 8 三线八角 ( http: / / www.21cnjy.com ) 同位角 ∠2和∠6；∠3和∠7；∠4和∠8 内错角； ∠4和∠6 同旁内角 ∠4和∠5
【解析】
略
三、解答题
1、 (1)见解析
(2)见解析
(3)见解析
(4)AH；
(5)AG＜AH＜BH，点到直线的距离，垂线段最短
【解析】
【分析】
（1）根据平行线的判定结合网格画AB的平行线CF即可；
（2）根据垂线的定义，结合网格过点A画线段BC的垂线段即可；
（3）根据垂线的定义，结合网格过点A画线段AB的垂线，交BC于点H即可；
（4）点H到直线AB的距离是过点H垂直于AB的垂线段HA的长；
（5）根据点到直线的距离，垂线段最短求解即可．
(1)
解：如图所示，直线CF即为所求；
( http: / / www.21cnjy.com / )
(2)
解：如图所示，线段AG即为所求；
( http: / / www.21cnjy.com / )
(3)
解：如图所示，线段AH即为所求；
( http: / / www.21cnjy.com / )
(4)
解：由题意得线段AH的长度是点H到直线AB的距离；
故答案为：AH；
(5)
解：∵AG⊥BH，
∴AG＜AH，
∵AH⊥AB，
∴AH＜BH，
∴AG＜AH＜BH，理由是：点到直线的距离，垂线段最短，
故答案为：AG＜AH＜BH，点到直线的距离，垂线段最短．
【点睛】
本题主要考查了画平行线，画垂线，点到直线的距离，垂线段最短等等，熟知相关知识是解题的关键．
2、证明见解析
【解析】
【分析】
由，证明，再证，最后根据对顶角相等，可得答案．
【详解】
证明：∵，
∴，
∴，
又∵，
∴，
∴，
∴，
∵，
∴．
【点睛】
本题主要考查了平行线的性质与判定，对顶角的性质，解题的关键在于能够熟练掌握相关知识进行求解．
3、80°．
【解析】
【分析】
先由平行线的性质得到∠ABD与∠D、∠ABC与∠C的关系，再结合角平分线的性质可得结论．
【详解】
解：∵AB//CD，
∴∠ABD=∠D=50°，∠ABC+∠C=180°．
∵BD平分∠ABC，
∴∠ABC=2∠ABD=100°．
∴∠C=180°-∠ABC
=180°-100°
=80°．
【点睛】
本题考查了平行线的性质，掌握“两直线平行，内错角相等、同旁内角互补”及角平分线的性质是解决本题的关键．www-2-1-cnjy-com
4、（1）见解析；（2）见解析；（3）见解析
【解析】
【分析】
（1）根据两点之间线段最短即连接CD，则CD与线段AB交于点P，此时PC+PD最小；
（2）根据图b可知∠B=45°，然后可在线段AB上找一点Q，使∠QCB=45°，则有CQ⊥AB，画出线段CQ；【来源：21cnj*y.co*m】
（3）根据网格图c可知∠A=45°，然后再格点中找到∠MCA=45°，则有∠A=∠MCA=45°，进而可知CM∥AB．【出处：21教育名师】
【详解】
解：（1）如图a，点P即为所求；
( http: / / www.21cnjy.com / )
（2）如图b，点Q和线段CQ即为所求；
( http: / / www.21cnjy.com / )
( http: / / www.21cnjy.com / )
（3）如图c，线段CM即为所求．
【点睛】
本题主要考查格点作图及结合了垂直的定义、平行线的性质等知识点，熟练掌握格点作图是解题的关键．
5、问题情境：；问题迁移：（1）；理由见解析；（2）当点在、两点之间时，；当点在射线上时，.
【解析】
【分析】
问题情境：理由平行于同一条直线的两条直线平行得到 PE∥AB∥CD，通过平行线性质来求∠APC；
（1）过点P作，得到理由平行线的性质得到，，即可得到；
（2）分情况讨论当点P在B、O两点之间，以及点P在射线AM上时，两种情况，然后构造平行线，利用两直线平行内错角相等，通过推理即可得到答案．
【详解】
解：问题情境：
( http: / / www.21cnjy.com / )
∵AB∥CD，PE∥AB，
∴PE∥AB∥CD，
∴∠A+∠APE=180°，∠C+∠CPE=180°，
∵∠PAB=130°，∠PCD=120°，
∴∠APE=50°，∠CPE=60°，
∴∠APC=∠APE+∠CPE=50°+60°=110°；
（1）；
过点P作，
( http: / / www.21cnjy.com / )
又因为，所以，
则，，
所以；
（2）情况1：如图所示，当点P在B、O两点之间时，
( http: / / www.21cnjy.com / )
过P作PE∥AD，交ON于E，
∵AD∥BC，
∴AD∥BC∥PE，
∴∠DPE=∠ADP=∠α，∠CPE=∠BCP=∠β，
∴∠CPD=∠DPE-∠CPE=∠α-∠β，
情况2：如图所示，点P在射线AM上时，
( http: / / www.21cnjy.com / )
过P作PE∥AD，交ON于E，
∵AD∥BC，
∴AD∥BC∥PE，
∴∠DPE=∠ADP=∠α，∠CPE=∠BCP=∠β，
∴∠CPD=∠CPE-∠DPE=∠β-∠α
【点睛】
本题主要考查了借助辅助线构造平行线，利用平行线的性质进行推理，准确分析证明是解题的关键．
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 （共 2 页）
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)