第11章 图形的平移与旋转同步训练试题(含解析)
文档属性
| 名称 | 第11章 图形的平移与旋转同步训练试题(含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-19 08:42:25 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
八年级数学下册第11章图形的平移与旋转同步训练
考试时间:90分钟;命题人:数学教研组
考生注意:
1、本卷分第I卷(选择题)和第Ⅱ卷(非选择题)两部分,满分100分,考试时间90分钟
2、答卷前,考生务必用0.5毫米黑色签字笔将自己的姓名、班级填写在试卷规定位置上
3、答案必须写在试卷各个题目指定区 ( http: / / www.21cnjy.com )域内相应的位置,如需改动,先划掉原来的答案,然后再写上新的答案;不准使用涂改液、胶带纸、修正带,不按以上要求作答的答案无效。21cnjy.com
第I卷(选择题 30分)
一、单选题(10小题,每小题3分,共计30分)
1、下列图形中既是中心对称图形又是轴对称图形的是( )
A. ( http: / / www.21cnjy.com / ) B. C. ( http: / / www.21cnjy.com / ) D. ( http: / / www.21cnjy.com / )
2、如图,在Rt△ABC中,∠C=90°,∠ABC=30°,AC=,将Rt△ABC绕点A逆时针旋转得到Rt△AB'C',连接BB',则BB'的长度是( )2·1·c·n·j·y
( http: / / www.21cnjy.com / )
A.1 B.3 C. D.2
3、在平面直角坐标系中,点的坐标是,点与点关于原点对称,则点的坐标是( )
A.(﹣2,1) B.(2,﹣1) C.(2,1) D.(﹣1,﹣2)
4、在以下图形中,是中心对称图形的是( )
A. B. C. D.
5、数学世界中充满了许多美 ( http: / / www.21cnjy.com )妙的几何图形,等待着你去发现,如图是张老师用几何画板画出的四个图形,其中既是轴对称图形又是中心对称图形的是( )www-2-1-cnjy-com
( http: / / www.21cnjy.com / )
A.①勾股树 B.②分形树
C.③谢尔宾斯三角形 D.④雪花
6、下列图形中,既是中心对称图形又是轴对称图形的是( )
A.平行四边形 B.等腰梯形 C.正方形 D.等腰三角形
7、在平面直角坐标系中,把点向左平移1个单位后所得的点的坐标是( )
A. B. C. D.
8、下列四个交通标志中,属于中心对称图形的是( )
A. ( http: / / www.21cnjy.com / ) B. ( http: / / www.21cnjy.com / )
C. D. ( http: / / www.21cnjy.com / )
9、下列图形中既是中心对称图形,又是轴对称图形的是( )
A. ( http: / / www.21cnjy.com / ) B. ( http: / / www.21cnjy.com / ) C. ( http: / / www.21cnjy.com / ) D. ( http: / / www.21cnjy.com / )
10、点N(3,﹣2)先向左平移3个单位,又向上平移2个单位得到点M,则点M的坐标为( )
A.(0,0) B.(0,﹣4) C.(6,﹣4) D.(6,0)
第Ⅱ卷(非选择题 70分)
二、填空题(5小题,每小题4分,共计20分)
1、定义:在平面内,一个点到图形的距离是这个点到这个图上所有点的最短距离,在平面内有一个正方形,边长为6,中心为O,在正方形外有一点P,,当正方形绕着点O旋转时,则点P到正方形的最短距离d的最大值为______.【来源:21·世纪·教育·网】
( http: / / www.21cnjy.com / )
2、如图,在△ABC中,∠CAB=45°,若∠CAB'=25°,则旋转角的度数为 _____.
( http: / / www.21cnjy.com / )
3、如图,在中,,,,将绕点按逆时针方向旋转得到,连接,,直线,相交于点,连接,在旋转过程中,线段的最大值为__________.
( http: / / www.21cnjy.com / )
4、如图,在△ABC中,∠B=60°,∠ ( http: / / www.21cnjy.com )C=75°,将△ABC绕点A顺时针旋转α(0°<α<180°)得到△ADE,若点C落在△ADE的边上,则α的度数是__________.21·世纪*教育网
( http: / / www.21cnjy.com / )
5、如图,在平面直角坐标系xOy中 ( http: / / www.21cnjy.com ),有一边长为1的正方形OABC,点B在x轴的正半轴上,如果以对角线OB为边作第二个正方形OBB1C1,再以对角线OB1为边作第三个正方形OB1B2C2,…,照此规律作下去,则B2的坐标是 ___;B2020的坐标是 ___.2-1-c-n-j-y
( http: / / www.21cnjy.com / )
三、解答题(5小题,每小题10分,共计50分)
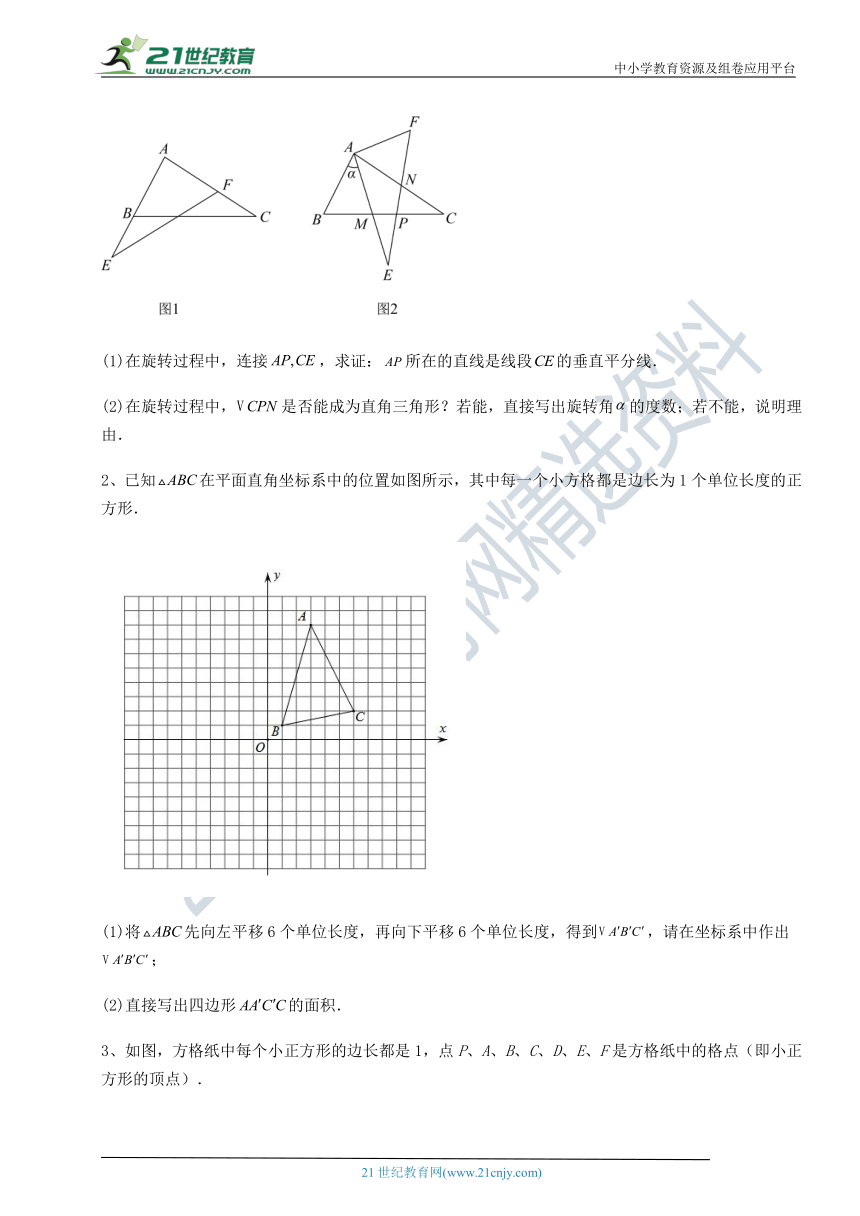
1、将两块完全相同的且含角的直角三角板和按如图所示位置放置,现将绕A点按逆时针方向旋转.如图,与交于点M,与交于点N,与交于点P.
( http: / / www.21cnjy.com / )
(1)在旋转过程中,连接,求证:所在的直线是线段的垂直平分线.
(2)在旋转过程中,是否能成为直角三角形?若能,直接写出旋转角的度数;若不能,说明理由.
2、已知在平面直角坐标系中的位置如图所示,其中每一个小方格都是边长为1个单位长度的正方形.
( http: / / www.21cnjy.com / )
(1)将先向左平移6个单位长度,再向下平移6个单位长度,得到,请在坐标系中作出;
(2)直接写出四边形的面积.
3、如图,方格纸中每个小正方形的边长都是1,点P、A、B、C、D、E、F是方格纸中的格点(即小正方形的顶点).21*cnjy*com
( http: / / www.21cnjy.com / )
(1)在图①中,过点P画出AB的平行线,过P点画出表示点P到直线AB距离的垂线段;
(2)在图②中,以线段AB、CD、EF的长为边长的三角形的面积等于 .
4、如图,中,,点D在AB上,,,于点E,把绕点D旋转得,且点G,F在AC上.
( http: / / www.21cnjy.com / )
(1)求证:四边形是正方形;
(2)求四边形的面积,
5、如图,每个小正方形的边长为1,每个小正方形的顶点叫格点,的三个顶点都在格点上,在图中画出将绕点C按顺时针方向旋转90°后得到的.21·cn·jy·com
( http: / / www.21cnjy.com / )
-参考答案-
一、单选题
1、C
【解析】
【分析】
根据中心对称图形和轴对称图形的定义判断即可.
【详解】
解:A.是轴对称图形,不是中心对称图形,故此选项不合题意;
B.是轴对称图形,不是中心对称图形,故此选项不合题意;
C.既是中心对称图形,也是轴对称图形,符合题意;
D.是中心对称图形,不是轴对称图形,故此选项不合题意.
故选:C.
【点睛】
本题考查中心对称图形和轴对称图形的知识,关 ( http: / / www.21cnjy.com )键是掌握好中心对称图形与轴对称图形的概念.轴对称图形的关键是寻找对称轴,图形两部分折叠后可重合,中心对称图形是要寻找对称中心,图形旋转180°后与原图重合.【出处:21教育名师】
2、D
【解析】
【分析】
先根据含30°角的直角三角形的性质求得∠BAC=60°,AB=2,再根据旋转性质得到∠BAB'=∠BAC=60°,AB=AB',根据等边三角形的判定与性质证明△ABB'是等边三角形即可求解.
【详解】
解:∵在Rt△ABC中,∠C=90°,∠ABC=30°,AC=,
∴∠BAC=90°-∠ABC=60°,AB=2AC=2,
∵将Rt△ABC绕点A逆时针旋转得到Rt△AB'C',
∴∠BAB'=∠BAC=60°,AB=AB',
∴△ABB'是等边三角形,
∴BB'=AB=2,
故选:D.
【点睛】
本题考查含30°角的直角三角形性质、旋转的性质、等边三角形的判定与性质,熟练掌握旋转的性质和等边三角形的判定是解答的关键.【版权所有:21教育】
3、C
【解析】
【分析】
直接利用关于原点对称点的性质,横纵坐标互为相反数得出答案.
【详解】
解:点的坐标是,点与点关于原点对称,
点的坐标是.
故选:C.
【点睛】
此题主要考查了关于原点对称点的性质,解题的关键是正确掌握相关运算法则.
4、B
【解析】
【分析】
在平面内,把一个图形绕着某 ( http: / / www.21cnjy.com )个点旋转180°,如果旋转后的图形能与原来的图形重合,那么这个图形叫做中心对称图形;根据中心对称图形的定义依次判断即可.【来源:21cnj*y.co*m】
【详解】
解:由图可知A、C、D均不是中心对称图形,B是中心对称图形
故选B.
【点睛】
本题考查了中心对称图形.解题的关键在于正确判断图形的对称性.
5、D
【解析】
【分析】
根据轴对称图形和中心对称图形的概念,对各选项分析判断即可得解.把一个图形绕某一点旋转,如果旋转后的图形能够与原来的图形重合,那么这个图形就叫做中心对称图形;如果一个图形沿一条直线折叠,直线两旁的部分能够互相重合,这个图形叫做轴对称图形.21教育名师原创作品
【详解】
解:A、①既不是轴对称图形,也不是中心对称图形,故本选项不符合题意;
B、②是轴对称图形,不是中心对称图形,故本选项不符合题意;
C、③是轴对称图形,不是中心对称图形,故本选项不符合题意;
D、④既是轴对称图形,又是中心对称图形,故本选项符合题意.
故选:D.
【点睛】
本题考查了中心对称图形与轴对称 ( http: / / www.21cnjy.com )图形的概念,轴对称图形的关键是寻找对称轴,图形两部分折叠后可重合,中心对称图形是要寻找对称中心,旋转180度后与原图重合.21*cnjy*com
6、C
【解析】
【分析】
根据轴对称图形与中心对称图形的概念,轴对称图形两部分沿对称轴折叠后可重合;中心对称图形是图形沿对称中心旋转180度后与原图重合.
【详解】
解:A.平行四边形是中心对称图形,不是轴对称图形,故本选项错误;
B.等腰梯形不是中心对称图形,是轴对称图形,故本选项错误;
C.正方形是中心对称图形,也是轴对称图形,故本选项正确;
D.等腰三角形不是中心对称图形,是轴对称图形,故本选项错误.
故选C.
【点睛】
本题考查了中心对称图形与轴对 ( http: / / www.21cnjy.com )称图形的概念:轴对称图形的关键是寻找对称轴,图形两部分折叠后可重合;中心对称图形是要寻找对称中心,旋转180度后两部分重合,掌握中心对称图形与轴对称图形的概念是解题的关键.
7、C
【解析】
【分析】
根据点坐标平移的性质,把点横坐标减一,纵坐标保持不变即可求解.
【详解】
解:把点向左平移1个单位,即横坐标减一,纵坐标保持不变,故把点向左平移1个单位后所得的点的坐标是.
故选:C.
【点睛】
此题考查了点坐标的平移问题,解题的关键是点坐标平移的性质.
8、D
【解析】
【分析】
根据中心对称图形的定义和交通标志的图案特点即可解答.
【详解】
解:A、不是中心对称图形,故不符合题意;
B、不是中心对称图形,故不符合题意;
C、不是中心对称图形,故不符合题意;
D、是中心对称图形,故本选项正确.
故选:D.
【点睛】
本题考查中心对称图形的概念:在同一平面内, ( http: / / www.21cnjy.com )如果把一个图形绕某一点旋转180度,旋转后的图形能和原图形完全重合,那么这个图形就叫做中心对称图形.
9、C
【解析】
【详解】
解:选项A,B中的图形是轴对称图形,不是中心对称图形,故A,B不符合题意;
选项C中的图形既是轴对称图形,也是中心对称图形,故C符合题意;
选项D中的图形不是轴对称图形,是中心对称图形,故D不符合题意,
故选C
【点睛】
本题考查的是轴对称图形与中心对称图形的识别,把一个图形沿某条直线对折,直线两旁的部分能够完全重合,则这个图形是轴对称图形,把一个图形绕某点旋转后能够与自身重合,则这个图形是中心对称图形,掌握“轴对称图形与中心对称图形的定义”是解本题的关键.
10、A
【解析】
【分析】
把点N的横坐标减3,纵坐标加2即可得到点M的坐标.
【详解】
解:根据题意得
点M的横坐标为3-3=0,纵坐标为-2+2=0,
∴点M的坐标为(0,0).
故选:A.
【点睛】
本题考查了点的平移规律;正确理解点的平移,左右平移只改变点的横坐标,左减右加;上下平移只改变点的纵坐标,上加下减是解题的关键.
二、填空题
1、3
【解析】
【分析】
由题意以及正方形的性质得OP过正方形ABCD各边的中点时,d最大,求出d的值即可得出答案
【详解】
解:如图:设AB的中点是E,OP过点E时,点O与边AB上所有点的连线中,OE最小,此时d=PE最大,
( http: / / www.21cnjy.com / )
∵正方形ABCD边长为6,O为正方形中心,
∴AE=3,∠OAE=45°,OE⊥AB,
∴OE=3,
∵OP=6,
∴d=PE=6-3=3;
故答案为:3
【点睛】
本题考查正方形的性质,旋转的性质,根据题意得出d最大时点P的位置是解题的关键.
2、20°##20度
【解析】
【分析】
根据题干所给角度即可直接求出的大小,即旋转角的大小.
【详解】
解:∵,
∴旋转角的度数为,
故答案为:20°.
【点睛】
本题考查旋转的性质.根据题意找出即为旋转角是解答本题的关键.
3、
【解析】
【分析】
取AB的中点H,连接CH、FH,设EC,DF交于点G,在△ABC中,由勾股定理得到AB=,由旋转可知:△DCE≌△ACB,从而∠DCA=∠BCE,∠ADC=∠BEC,由∠DGC=∠EGF,可得∠AFB=90 ,由直角三角形斜边上的中线等于斜边的一半,可得FH=CH=AB=,在△FCH中,当F、C、H在一条直线上时,CF有最大值为.
【详解】
解:取AB的中点H,连接CH、FH,设EC,DF交于点G,
( http: / / www.21cnjy.com / )
在△ABC中,∠ACB=90 ,
∵AC=,BC=2,
∴AB=,
由旋转可知:△DCE≌△ACB,
∴∠DCE=∠ACB,DC=AC,CE=CB,
∴∠DCA=∠BCE,
∵∠ADC=(180 -∠ACD) ,∠BEC= (180 -∠BCE),
∴∠ADC=∠BEC,
∵∠DGC=∠EGF,
∴∠DCG=∠EFG=90 ,
∴∠AFB=90 ,
∵H是AB的中点,
∴FH=AB,
∵∠ACB=90 ,
∴CH=AB,
∴FH=CH=AB=,
在△FCH中,FH+CH>CF,
当F、C、H在一条直线上时,CF有最大值,
∴线段CF的最大值为.
故答案为:
【点睛】
本题考查了旋转的性质、勾股定理,解决本题的关键是掌握全等的性质.
4、或
【解析】
【分析】
分两种情况:当点C在边AD上,当点C在边DE上,由旋转的性质及三角形内角和定理可求出答案.
【详解】
解:当点C在边AD上,如图1,
( http: / / www.21cnjy.com / )
∵,
∴,
∵将△ABC绕点A顺时针旋转得到△ADE,
∴,
如图2,当点C在边DE上,
( http: / / www.21cnjy.com / )
∵将△ABC绕点A顺时针旋转得到△ADE,
∴,
∴,
∴.
综合以上可得α的度数是或.
故答案为:或.
【点睛】
本题考查旋转的性质,三角形内角和定理.利用分类讨论的思想是解答本题的关键.
5、
【解析】
【分析】
根据已知条件和勾股定理求出OB2的长度即可求出B2的坐标,再根据题意和图形可看出每经过一次变化,正方形都逆时针旋转45°,正方形的边长都乘以所以可求出从B到B2020变化的坐标.
【详解】
解:∵四边形OABC是边长为1正方形,
∴
∴
∴B1的坐标是,
∴,
∴B2的坐标是
根据题意和图形可看出每经过一次变化,正方形逆时针旋转45°,其边长乘以,
∴B3的坐标是
∴B4的坐标是
∴旋转8次则OB旋转一周,
∵从B到B2020经过了2020次变化,2020÷8=252…4,
∴从B到B2020与B4都在x轴负半轴上,
∴点B2020的坐标是
【点睛】
本题主要考查了规律型-点的坐标,解决本题的关键是利用正方形的变化过程寻找点的变化规律.
三、解答题
1、 (1)见解析;
(2)能成为直角三角形,=30°或60°
【解析】
【分析】
(1)由全等三角形的性质可得∠AEF ( http: / / www.21cnjy.com )=∠ACB,AE=AC,根据等腰三角形的判定与性质证明∠PEC=∠PCE,PE=PC,然后根据线段垂直平分线的判定定理即可证得结论;21教育网
(2)分∠CPN=90°和∠CNP=90°,利用旋转的性质和三角形的内角和定理求解即可.
(1)
证明:∵两块是完全相同的且含角的直角三角板和,
∴AE=AC,∠AEF=∠ACB=30°,∠F=60°,
∴∠AEC=∠ACE,
∴∠AEC-∠AEF=∠ACE-∠ACB,
∴∠PEC=∠PCE,
∴PE=PC,又AE=AC,
∴所在的直线是线段的垂直平分线.
( http: / / www.21cnjy.com / )
(2)
解:在旋转过程中,能成为直角三角形,
由旋转的性质得:∠FAC= ,
当∠CNP=90°时,∠FNA=90°,又∠F=60°,
∴=∠FAC=180°-∠FNA-∠F=180°-90°-60°=30°;
当∠CPN=90°时,∵∠NCP=30°,
∴∠PNC=180°-90°-30°=60°,即∠FNA=60°,
∵∠F=60°,
∴=∠FAC=180°-∠FNA-∠F=180°-60°-60°=60°,
综上,旋转角的的度数为30°或60°.
【点睛】
本题考查直角三角板的度数、全等三角形的性质 ( http: / / www.21cnjy.com )、等腰三角形的判定与性质、线段垂直平分线的判定、旋转性质、对顶角相等、三角形的内角和定理,熟练掌握相关知识的联系与运用是解答的关键.
2、 (1)见解析
(2)54
【解析】
【分析】
(1)分别作出点A、B、C平移后得到对应点,再顺次连接即可;
(2)利用两个三角形的面积和计算即可.
(1)
解:如图所示,是所求作三角形;
( http: / / www.21cnjy.com / )
(2)
解:;
;
四边形的面积为27+27=54.
【点睛】
本题主要考查作图-平移变换,解题的关键是熟练掌握平移变换的性质,会用面积和差计算面积.
3、 (1)见解析
(2)4
【解析】
【分析】
(1)直接利用网格结合勾股定理得出答案;
(2)利用平移的性质得出以线段AB、CD、EF的长为边长的三角形的面积等于△ABM的面积,进而得出答案.www.21-cn-jy.com
(1)
解:如图①所示:MN∥AB,PD⊥AB;
( http: / / www.21cnjy.com / ),
(2)
解:如图②所示:
( http: / / www.21cnjy.com / )
以线段AB、CD、EF的长为边长的三角形的面积等于△ABM的面积为:
3×4-×1×2-×2×3-×2×4=4.
故答案为:4.
【点睛】
本题主要考查了应用设计与作图,正确平移线段是解题关键.
4、 (1)见解析
(2)
【解析】
【分析】
(1)根据旋转的性质可得≌,进而可得,根据三个角是直角的四边形证明四边形CEDF是矩形,根据邻边相等的矩形是正方形即可得证;21世纪教育网版权所有
(2)在中,根据勾股定理得根据等面积法即可求得,进而求得正方形的面积.
(1)
∵,
∴.
由旋转得:,≌.
∴.
∵,
∴四边形CEDF是矩形.
∵,
∴四边形CEDF是正方形.
( http: / / www.21cnjy.com / )
(2)
由(1)得:四边形CEDF是正方形,
∴.
由旋转得:≌,.
∴,.
在中,根据勾股定理得:.
∵,
∴.
∴.
∴.
【点睛】
本题考查了正方形的性质与判定,勾股定理,旋转的性质,全等的性质,掌握以上性质定理是解题的关键.
5、作图见解析
【解析】
【分析】
分别确定绕顺时针旋转后的对应点,再顺次连接即可.
【详解】
解:如图,是所求作的三角形
( http: / / www.21cnjy.com / )
【点睛】
本题考查的是旋转的作图,熟悉旋转的性质,再进行作图是解本题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
八年级数学下册第11章图形的平移与旋转同步训练
考试时间:90分钟;命题人:数学教研组
考生注意:
1、本卷分第I卷(选择题)和第Ⅱ卷(非选择题)两部分,满分100分,考试时间90分钟
2、答卷前,考生务必用0.5毫米黑色签字笔将自己的姓名、班级填写在试卷规定位置上
3、答案必须写在试卷各个题目指定区 ( http: / / www.21cnjy.com )域内相应的位置,如需改动,先划掉原来的答案,然后再写上新的答案;不准使用涂改液、胶带纸、修正带,不按以上要求作答的答案无效。21cnjy.com
第I卷(选择题 30分)
一、单选题(10小题,每小题3分,共计30分)
1、下列图形中既是中心对称图形又是轴对称图形的是( )
A. ( http: / / www.21cnjy.com / ) B. C. ( http: / / www.21cnjy.com / ) D. ( http: / / www.21cnjy.com / )
2、如图,在Rt△ABC中,∠C=90°,∠ABC=30°,AC=,将Rt△ABC绕点A逆时针旋转得到Rt△AB'C',连接BB',则BB'的长度是( )2·1·c·n·j·y
( http: / / www.21cnjy.com / )
A.1 B.3 C. D.2
3、在平面直角坐标系中,点的坐标是,点与点关于原点对称,则点的坐标是( )
A.(﹣2,1) B.(2,﹣1) C.(2,1) D.(﹣1,﹣2)
4、在以下图形中,是中心对称图形的是( )
A. B. C. D.
5、数学世界中充满了许多美 ( http: / / www.21cnjy.com )妙的几何图形,等待着你去发现,如图是张老师用几何画板画出的四个图形,其中既是轴对称图形又是中心对称图形的是( )www-2-1-cnjy-com
( http: / / www.21cnjy.com / )
A.①勾股树 B.②分形树
C.③谢尔宾斯三角形 D.④雪花
6、下列图形中,既是中心对称图形又是轴对称图形的是( )
A.平行四边形 B.等腰梯形 C.正方形 D.等腰三角形
7、在平面直角坐标系中,把点向左平移1个单位后所得的点的坐标是( )
A. B. C. D.
8、下列四个交通标志中,属于中心对称图形的是( )
A. ( http: / / www.21cnjy.com / ) B. ( http: / / www.21cnjy.com / )
C. D. ( http: / / www.21cnjy.com / )
9、下列图形中既是中心对称图形,又是轴对称图形的是( )
A. ( http: / / www.21cnjy.com / ) B. ( http: / / www.21cnjy.com / ) C. ( http: / / www.21cnjy.com / ) D. ( http: / / www.21cnjy.com / )
10、点N(3,﹣2)先向左平移3个单位,又向上平移2个单位得到点M,则点M的坐标为( )
A.(0,0) B.(0,﹣4) C.(6,﹣4) D.(6,0)
第Ⅱ卷(非选择题 70分)
二、填空题(5小题,每小题4分,共计20分)
1、定义:在平面内,一个点到图形的距离是这个点到这个图上所有点的最短距离,在平面内有一个正方形,边长为6,中心为O,在正方形外有一点P,,当正方形绕着点O旋转时,则点P到正方形的最短距离d的最大值为______.【来源:21·世纪·教育·网】
( http: / / www.21cnjy.com / )
2、如图,在△ABC中,∠CAB=45°,若∠CAB'=25°,则旋转角的度数为 _____.
( http: / / www.21cnjy.com / )
3、如图,在中,,,,将绕点按逆时针方向旋转得到,连接,,直线,相交于点,连接,在旋转过程中,线段的最大值为__________.
( http: / / www.21cnjy.com / )
4、如图,在△ABC中,∠B=60°,∠ ( http: / / www.21cnjy.com )C=75°,将△ABC绕点A顺时针旋转α(0°<α<180°)得到△ADE,若点C落在△ADE的边上,则α的度数是__________.21·世纪*教育网
( http: / / www.21cnjy.com / )
5、如图,在平面直角坐标系xOy中 ( http: / / www.21cnjy.com ),有一边长为1的正方形OABC,点B在x轴的正半轴上,如果以对角线OB为边作第二个正方形OBB1C1,再以对角线OB1为边作第三个正方形OB1B2C2,…,照此规律作下去,则B2的坐标是 ___;B2020的坐标是 ___.2-1-c-n-j-y
( http: / / www.21cnjy.com / )
三、解答题(5小题,每小题10分,共计50分)
1、将两块完全相同的且含角的直角三角板和按如图所示位置放置,现将绕A点按逆时针方向旋转.如图,与交于点M,与交于点N,与交于点P.
( http: / / www.21cnjy.com / )
(1)在旋转过程中,连接,求证:所在的直线是线段的垂直平分线.
(2)在旋转过程中,是否能成为直角三角形?若能,直接写出旋转角的度数;若不能,说明理由.
2、已知在平面直角坐标系中的位置如图所示,其中每一个小方格都是边长为1个单位长度的正方形.
( http: / / www.21cnjy.com / )
(1)将先向左平移6个单位长度,再向下平移6个单位长度,得到,请在坐标系中作出;
(2)直接写出四边形的面积.
3、如图,方格纸中每个小正方形的边长都是1,点P、A、B、C、D、E、F是方格纸中的格点(即小正方形的顶点).21*cnjy*com
( http: / / www.21cnjy.com / )
(1)在图①中,过点P画出AB的平行线,过P点画出表示点P到直线AB距离的垂线段;
(2)在图②中,以线段AB、CD、EF的长为边长的三角形的面积等于 .
4、如图,中,,点D在AB上,,,于点E,把绕点D旋转得,且点G,F在AC上.
( http: / / www.21cnjy.com / )
(1)求证:四边形是正方形;
(2)求四边形的面积,
5、如图,每个小正方形的边长为1,每个小正方形的顶点叫格点,的三个顶点都在格点上,在图中画出将绕点C按顺时针方向旋转90°后得到的.21·cn·jy·com
( http: / / www.21cnjy.com / )
-参考答案-
一、单选题
1、C
【解析】
【分析】
根据中心对称图形和轴对称图形的定义判断即可.
【详解】
解:A.是轴对称图形,不是中心对称图形,故此选项不合题意;
B.是轴对称图形,不是中心对称图形,故此选项不合题意;
C.既是中心对称图形,也是轴对称图形,符合题意;
D.是中心对称图形,不是轴对称图形,故此选项不合题意.
故选:C.
【点睛】
本题考查中心对称图形和轴对称图形的知识,关 ( http: / / www.21cnjy.com )键是掌握好中心对称图形与轴对称图形的概念.轴对称图形的关键是寻找对称轴,图形两部分折叠后可重合,中心对称图形是要寻找对称中心,图形旋转180°后与原图重合.【出处:21教育名师】
2、D
【解析】
【分析】
先根据含30°角的直角三角形的性质求得∠BAC=60°,AB=2,再根据旋转性质得到∠BAB'=∠BAC=60°,AB=AB',根据等边三角形的判定与性质证明△ABB'是等边三角形即可求解.
【详解】
解:∵在Rt△ABC中,∠C=90°,∠ABC=30°,AC=,
∴∠BAC=90°-∠ABC=60°,AB=2AC=2,
∵将Rt△ABC绕点A逆时针旋转得到Rt△AB'C',
∴∠BAB'=∠BAC=60°,AB=AB',
∴△ABB'是等边三角形,
∴BB'=AB=2,
故选:D.
【点睛】
本题考查含30°角的直角三角形性质、旋转的性质、等边三角形的判定与性质,熟练掌握旋转的性质和等边三角形的判定是解答的关键.【版权所有:21教育】
3、C
【解析】
【分析】
直接利用关于原点对称点的性质,横纵坐标互为相反数得出答案.
【详解】
解:点的坐标是,点与点关于原点对称,
点的坐标是.
故选:C.
【点睛】
此题主要考查了关于原点对称点的性质,解题的关键是正确掌握相关运算法则.
4、B
【解析】
【分析】
在平面内,把一个图形绕着某 ( http: / / www.21cnjy.com )个点旋转180°,如果旋转后的图形能与原来的图形重合,那么这个图形叫做中心对称图形;根据中心对称图形的定义依次判断即可.【来源:21cnj*y.co*m】
【详解】
解:由图可知A、C、D均不是中心对称图形,B是中心对称图形
故选B.
【点睛】
本题考查了中心对称图形.解题的关键在于正确判断图形的对称性.
5、D
【解析】
【分析】
根据轴对称图形和中心对称图形的概念,对各选项分析判断即可得解.把一个图形绕某一点旋转,如果旋转后的图形能够与原来的图形重合,那么这个图形就叫做中心对称图形;如果一个图形沿一条直线折叠,直线两旁的部分能够互相重合,这个图形叫做轴对称图形.21教育名师原创作品
【详解】
解:A、①既不是轴对称图形,也不是中心对称图形,故本选项不符合题意;
B、②是轴对称图形,不是中心对称图形,故本选项不符合题意;
C、③是轴对称图形,不是中心对称图形,故本选项不符合题意;
D、④既是轴对称图形,又是中心对称图形,故本选项符合题意.
故选:D.
【点睛】
本题考查了中心对称图形与轴对称 ( http: / / www.21cnjy.com )图形的概念,轴对称图形的关键是寻找对称轴,图形两部分折叠后可重合,中心对称图形是要寻找对称中心,旋转180度后与原图重合.21*cnjy*com
6、C
【解析】
【分析】
根据轴对称图形与中心对称图形的概念,轴对称图形两部分沿对称轴折叠后可重合;中心对称图形是图形沿对称中心旋转180度后与原图重合.
【详解】
解:A.平行四边形是中心对称图形,不是轴对称图形,故本选项错误;
B.等腰梯形不是中心对称图形,是轴对称图形,故本选项错误;
C.正方形是中心对称图形,也是轴对称图形,故本选项正确;
D.等腰三角形不是中心对称图形,是轴对称图形,故本选项错误.
故选C.
【点睛】
本题考查了中心对称图形与轴对 ( http: / / www.21cnjy.com )称图形的概念:轴对称图形的关键是寻找对称轴,图形两部分折叠后可重合;中心对称图形是要寻找对称中心,旋转180度后两部分重合,掌握中心对称图形与轴对称图形的概念是解题的关键.
7、C
【解析】
【分析】
根据点坐标平移的性质,把点横坐标减一,纵坐标保持不变即可求解.
【详解】
解:把点向左平移1个单位,即横坐标减一,纵坐标保持不变,故把点向左平移1个单位后所得的点的坐标是.
故选:C.
【点睛】
此题考查了点坐标的平移问题,解题的关键是点坐标平移的性质.
8、D
【解析】
【分析】
根据中心对称图形的定义和交通标志的图案特点即可解答.
【详解】
解:A、不是中心对称图形,故不符合题意;
B、不是中心对称图形,故不符合题意;
C、不是中心对称图形,故不符合题意;
D、是中心对称图形,故本选项正确.
故选:D.
【点睛】
本题考查中心对称图形的概念:在同一平面内, ( http: / / www.21cnjy.com )如果把一个图形绕某一点旋转180度,旋转后的图形能和原图形完全重合,那么这个图形就叫做中心对称图形.
9、C
【解析】
【详解】
解:选项A,B中的图形是轴对称图形,不是中心对称图形,故A,B不符合题意;
选项C中的图形既是轴对称图形,也是中心对称图形,故C符合题意;
选项D中的图形不是轴对称图形,是中心对称图形,故D不符合题意,
故选C
【点睛】
本题考查的是轴对称图形与中心对称图形的识别,把一个图形沿某条直线对折,直线两旁的部分能够完全重合,则这个图形是轴对称图形,把一个图形绕某点旋转后能够与自身重合,则这个图形是中心对称图形,掌握“轴对称图形与中心对称图形的定义”是解本题的关键.
10、A
【解析】
【分析】
把点N的横坐标减3,纵坐标加2即可得到点M的坐标.
【详解】
解:根据题意得
点M的横坐标为3-3=0,纵坐标为-2+2=0,
∴点M的坐标为(0,0).
故选:A.
【点睛】
本题考查了点的平移规律;正确理解点的平移,左右平移只改变点的横坐标,左减右加;上下平移只改变点的纵坐标,上加下减是解题的关键.
二、填空题
1、3
【解析】
【分析】
由题意以及正方形的性质得OP过正方形ABCD各边的中点时,d最大,求出d的值即可得出答案
【详解】
解:如图:设AB的中点是E,OP过点E时,点O与边AB上所有点的连线中,OE最小,此时d=PE最大,
( http: / / www.21cnjy.com / )
∵正方形ABCD边长为6,O为正方形中心,
∴AE=3,∠OAE=45°,OE⊥AB,
∴OE=3,
∵OP=6,
∴d=PE=6-3=3;
故答案为:3
【点睛】
本题考查正方形的性质,旋转的性质,根据题意得出d最大时点P的位置是解题的关键.
2、20°##20度
【解析】
【分析】
根据题干所给角度即可直接求出的大小,即旋转角的大小.
【详解】
解:∵,
∴旋转角的度数为,
故答案为:20°.
【点睛】
本题考查旋转的性质.根据题意找出即为旋转角是解答本题的关键.
3、
【解析】
【分析】
取AB的中点H,连接CH、FH,设EC,DF交于点G,在△ABC中,由勾股定理得到AB=,由旋转可知:△DCE≌△ACB,从而∠DCA=∠BCE,∠ADC=∠BEC,由∠DGC=∠EGF,可得∠AFB=90 ,由直角三角形斜边上的中线等于斜边的一半,可得FH=CH=AB=,在△FCH中,当F、C、H在一条直线上时,CF有最大值为.
【详解】
解:取AB的中点H,连接CH、FH,设EC,DF交于点G,
( http: / / www.21cnjy.com / )
在△ABC中,∠ACB=90 ,
∵AC=,BC=2,
∴AB=,
由旋转可知:△DCE≌△ACB,
∴∠DCE=∠ACB,DC=AC,CE=CB,
∴∠DCA=∠BCE,
∵∠ADC=(180 -∠ACD) ,∠BEC= (180 -∠BCE),
∴∠ADC=∠BEC,
∵∠DGC=∠EGF,
∴∠DCG=∠EFG=90 ,
∴∠AFB=90 ,
∵H是AB的中点,
∴FH=AB,
∵∠ACB=90 ,
∴CH=AB,
∴FH=CH=AB=,
在△FCH中,FH+CH>CF,
当F、C、H在一条直线上时,CF有最大值,
∴线段CF的最大值为.
故答案为:
【点睛】
本题考查了旋转的性质、勾股定理,解决本题的关键是掌握全等的性质.
4、或
【解析】
【分析】
分两种情况:当点C在边AD上,当点C在边DE上,由旋转的性质及三角形内角和定理可求出答案.
【详解】
解:当点C在边AD上,如图1,
( http: / / www.21cnjy.com / )
∵,
∴,
∵将△ABC绕点A顺时针旋转得到△ADE,
∴,
如图2,当点C在边DE上,
( http: / / www.21cnjy.com / )
∵将△ABC绕点A顺时针旋转得到△ADE,
∴,
∴,
∴.
综合以上可得α的度数是或.
故答案为:或.
【点睛】
本题考查旋转的性质,三角形内角和定理.利用分类讨论的思想是解答本题的关键.
5、
【解析】
【分析】
根据已知条件和勾股定理求出OB2的长度即可求出B2的坐标,再根据题意和图形可看出每经过一次变化,正方形都逆时针旋转45°,正方形的边长都乘以所以可求出从B到B2020变化的坐标.
【详解】
解:∵四边形OABC是边长为1正方形,
∴
∴
∴B1的坐标是,
∴,
∴B2的坐标是
根据题意和图形可看出每经过一次变化,正方形逆时针旋转45°,其边长乘以,
∴B3的坐标是
∴B4的坐标是
∴旋转8次则OB旋转一周,
∵从B到B2020经过了2020次变化,2020÷8=252…4,
∴从B到B2020与B4都在x轴负半轴上,
∴点B2020的坐标是
【点睛】
本题主要考查了规律型-点的坐标,解决本题的关键是利用正方形的变化过程寻找点的变化规律.
三、解答题
1、 (1)见解析;
(2)能成为直角三角形,=30°或60°
【解析】
【分析】
(1)由全等三角形的性质可得∠AEF ( http: / / www.21cnjy.com )=∠ACB,AE=AC,根据等腰三角形的判定与性质证明∠PEC=∠PCE,PE=PC,然后根据线段垂直平分线的判定定理即可证得结论;21教育网
(2)分∠CPN=90°和∠CNP=90°,利用旋转的性质和三角形的内角和定理求解即可.
(1)
证明:∵两块是完全相同的且含角的直角三角板和,
∴AE=AC,∠AEF=∠ACB=30°,∠F=60°,
∴∠AEC=∠ACE,
∴∠AEC-∠AEF=∠ACE-∠ACB,
∴∠PEC=∠PCE,
∴PE=PC,又AE=AC,
∴所在的直线是线段的垂直平分线.
( http: / / www.21cnjy.com / )
(2)
解:在旋转过程中,能成为直角三角形,
由旋转的性质得:∠FAC= ,
当∠CNP=90°时,∠FNA=90°,又∠F=60°,
∴=∠FAC=180°-∠FNA-∠F=180°-90°-60°=30°;
当∠CPN=90°时,∵∠NCP=30°,
∴∠PNC=180°-90°-30°=60°,即∠FNA=60°,
∵∠F=60°,
∴=∠FAC=180°-∠FNA-∠F=180°-60°-60°=60°,
综上,旋转角的的度数为30°或60°.
【点睛】
本题考查直角三角板的度数、全等三角形的性质 ( http: / / www.21cnjy.com )、等腰三角形的判定与性质、线段垂直平分线的判定、旋转性质、对顶角相等、三角形的内角和定理,熟练掌握相关知识的联系与运用是解答的关键.
2、 (1)见解析
(2)54
【解析】
【分析】
(1)分别作出点A、B、C平移后得到对应点,再顺次连接即可;
(2)利用两个三角形的面积和计算即可.
(1)
解:如图所示,是所求作三角形;
( http: / / www.21cnjy.com / )
(2)
解:;
;
四边形的面积为27+27=54.
【点睛】
本题主要考查作图-平移变换,解题的关键是熟练掌握平移变换的性质,会用面积和差计算面积.
3、 (1)见解析
(2)4
【解析】
【分析】
(1)直接利用网格结合勾股定理得出答案;
(2)利用平移的性质得出以线段AB、CD、EF的长为边长的三角形的面积等于△ABM的面积,进而得出答案.www.21-cn-jy.com
(1)
解:如图①所示:MN∥AB,PD⊥AB;
( http: / / www.21cnjy.com / ),
(2)
解:如图②所示:
( http: / / www.21cnjy.com / )
以线段AB、CD、EF的长为边长的三角形的面积等于△ABM的面积为:
3×4-×1×2-×2×3-×2×4=4.
故答案为:4.
【点睛】
本题主要考查了应用设计与作图,正确平移线段是解题关键.
4、 (1)见解析
(2)
【解析】
【分析】
(1)根据旋转的性质可得≌,进而可得,根据三个角是直角的四边形证明四边形CEDF是矩形,根据邻边相等的矩形是正方形即可得证;21世纪教育网版权所有
(2)在中,根据勾股定理得根据等面积法即可求得,进而求得正方形的面积.
(1)
∵,
∴.
由旋转得:,≌.
∴.
∵,
∴四边形CEDF是矩形.
∵,
∴四边形CEDF是正方形.
( http: / / www.21cnjy.com / )
(2)
由(1)得:四边形CEDF是正方形,
∴.
由旋转得:≌,.
∴,.
在中,根据勾股定理得:.
∵,
∴.
∴.
∴.
【点睛】
本题考查了正方形的性质与判定,勾股定理,旋转的性质,全等的性质,掌握以上性质定理是解题的关键.
5、作图见解析
【解析】
【分析】
分别确定绕顺时针旋转后的对应点,再顺次连接即可.
【详解】
解:如图,是所求作的三角形
( http: / / www.21cnjy.com / )
【点睛】
本题考查的是旋转的作图,熟悉旋转的性质,再进行作图是解本题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
- 第6章 平行四边形
- 6.1 平行四边形及其性质
- 6.2 平行四边形的判定
- 6.3 特殊的平行四边形
- 6.4 三角形的中位线定理
- 第7章 实数
- 7.1 算术平方根
- 7.2 勾股定理
- 7.3 根号2是有理数吗
- 7.4 勾股定理的逆定理
- 7.5 平方根
- 7.6 立方根
- 7.7 用计算器求平方根和立方根
- 7.8 实数
- 第8章 一元一次不等式
- 8.1 不等式的基本性质
- 8.2 一元一次不等式
- 8.3 列一元一次不等式解应用题
- 8.4 一元一次不等式组
- 第9章 二次根式
- 9.1 二次根式和它的性质
- 9.2 二次根式的加法与减法
- 9.3 二次根式的乘法与除法
- 第10章 一次函数
- 10.1 函数的图像
- 10.2 一次函数和它的图像
- 10.3 一次函数的性质
- 10.4 一次函数与二元一次方程
- 10.5 一次函数与一元一次不等式
- 10.6 一次函数的应用
- 第11章 图形的平移与旋转
- 11.1 图形的平移
- 11.2 图形的旋转
- 11.3 图形的中心对称
