第14章 位置与坐标单元测试试题(含解析)
文档属性
| 名称 | 第14章 位置与坐标单元测试试题(含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-19 00:00:00 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
七年级数学下册第14章位置与坐标单元测试
考试时间:90分钟;命题人:数学教研组
考生注意:
1、本卷分第I卷(选择题)和第Ⅱ卷(非选择题)两部分,满分100分,考试时间90分钟
2、答卷前,考生务必用0.5毫米黑色签字笔将自己的姓名、班级填写在试卷规定位置上
3、答案必须写在试卷各个题目指定区域 ( http: / / www.21cnjy.com )内相应的位置,如需改动,先划掉原来的答案,然后再写上新的答案;不准使用涂改液、胶带纸、修正带,不按以上要求作答的答案无效。21教育网
第I卷(选择题 30分)
一、单选题(10小题,每小题3分,共计30分)
1、根据下列表述,能够确定具体位置的是( )
A.北偏东25°方向 B.距学校800米处
C.温州大剧院音乐厅8排 D.东经20°北纬30°
2、在平面直角坐标系中,点所在的象限是( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
3、如图,每个小正方形的边长为1,在阴影区域的点是( )
( http: / / www.21cnjy.com / )
A.(1,2) B.(﹣1,﹣2) C.(﹣1,2) D.(1,﹣2)
4、平面直角坐标系中,点到y轴的距离是( )
A.1 B.2 C.3 D.4
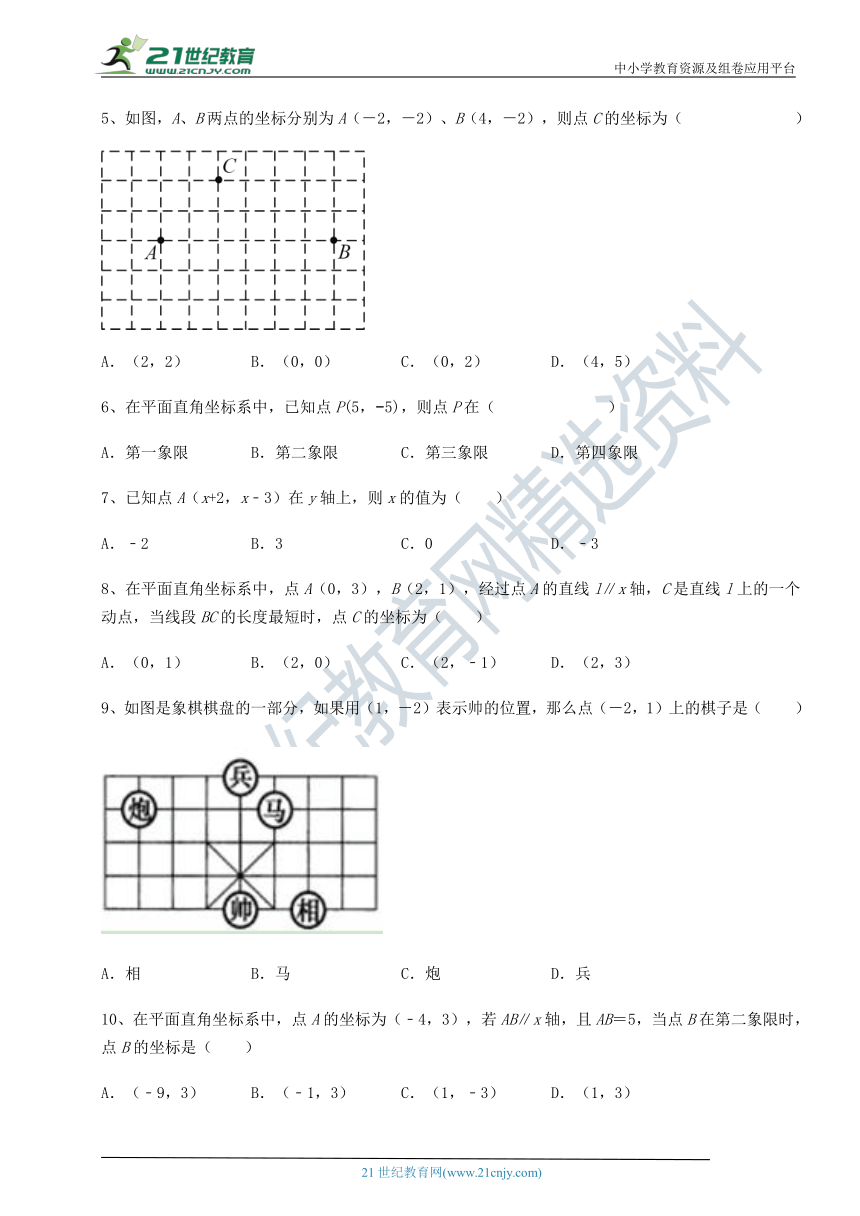
5、如图,A、B两点的坐标分别为A(-2,-2)、B(4,-2),则点C的坐标为( )
( http: / / www.21cnjy.com / )
A.(2,2) B.(0,0) C.(0,2) D.(4,5)
6、在平面直角坐标系中,已知点P(5, 5),则点P在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
7、已知点A(x+2,x﹣3)在y轴上,则x的值为( )
A.﹣2 B.3 C.0 D.﹣3
8、在平面直角坐标系中,点 ( http: / / www.21cnjy.com )A(0,3),B(2,1),经过点A的直线l∥x轴,C是直线l上的一个动点,当线段BC的长度最短时,点C的坐标为( )21cnjy.com
A.(0,1) B.(2,0) C.(2,﹣1) D.(2,3)
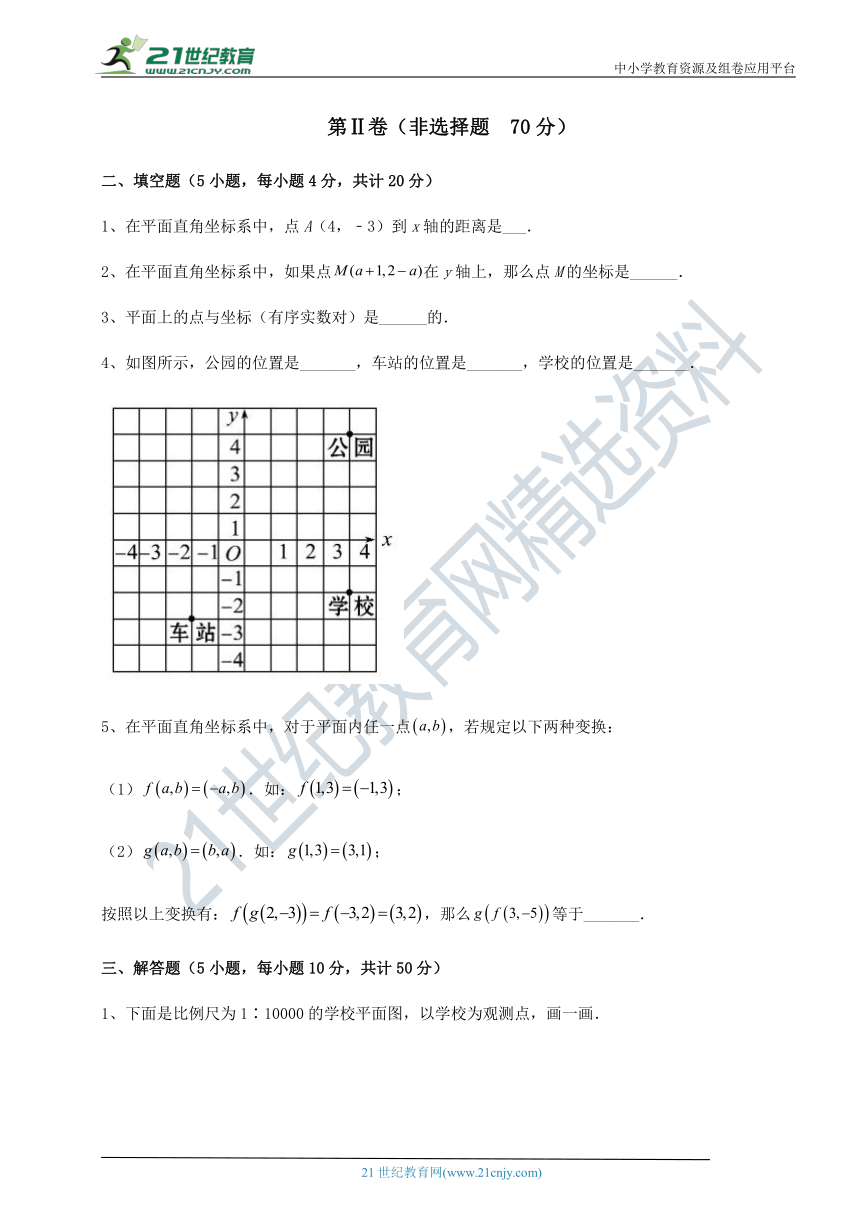
9、如图是象棋棋盘的一部分,如果用(1,-2)表示帅的位置,那么点(-2,1)上的棋子是( )
( http: / / www.21cnjy.com / )
A.相 B.马 C.炮 D.兵
10、在平面直角坐标系中,点A的坐标为(﹣4,3),若AB∥x轴,且AB=5,当点B在第二象限时,点B的坐标是( )2·1·c·n·j·y
A.(﹣9,3) B.(﹣1,3) C.(1,﹣3) D.(1,3)
第Ⅱ卷(非选择题 70分)
二、填空题(5小题,每小题4分,共计20分)
1、在平面直角坐标系中,点A(4,﹣3)到x轴的距离是___.
2、在平面直角坐标系中,如果点在y轴上,那么点M的坐标是______.
3、平面上的点与坐标(有序实数对)是______的.
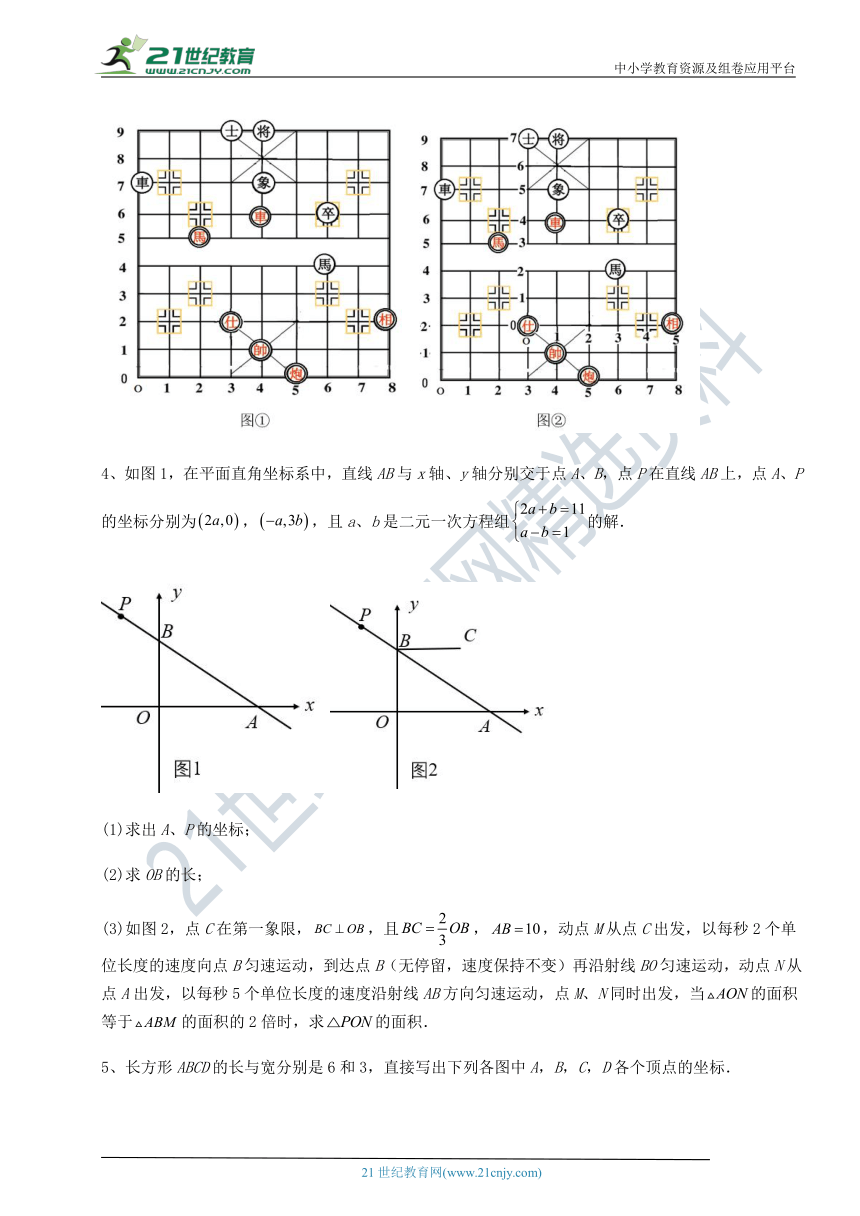
4、如图所示,公园的位置是_______,车站的位置是_______,学校的位置是_______.
( http: / / www.21cnjy.com / )
5、在平面直角坐标系中,对于平面内任一点,若规定以下两种变换:
(1).如:;
(2).如:;
按照以上变换有:,那么等于_______.
三、解答题(5小题,每小题10分,共计50分)
1、下面是比例尺为1∶10000的学校平面图,以学校为观测点,画一画.
( http: / / www.21cnjy.com / )
(1)少年宫在学校北偏东方向260米处.
(2)公园在学校南偏西方向300米处.
2、如图,五个学生正在做游戏,建立适当的直角坐标系,写出这五个学生所在位置的坐标.
( http: / / www.21cnjy.com / )
3、如图回答下列问题:
(1)如图①所示,请用有序数对写出棋盘上棋子“帅、黑车、炮”的位置(把列号写在前面,行号写在后面).2-1-c-n-j-y
(2)如图②所示把O点移动到棋子“仕”的位置时,用有序数对写出棋子“仕、相、黑马”的位置(把列号写在前面,行号写在后面)【出处:21教育名师】
(3)如图②,已知棋子“将”的位置是(2,8 ( http: / / www.21cnjy.com )),棋子“黑马”的位置是(4,3),规定列在前,行在后,请你在棋盘上确定A(0,0)点的位置,棋子“红马”的位置是什么? 【版权所有:21教育】
( http: / / www.21cnjy.com / )
4、如图1,在平面直角坐标系中,直线AB与x轴、y轴分别交于点A、B,点P在直线AB上,点A、P的坐标分别为,,且a、b是二元一次方程组的解.21教育名师原创作品
( http: / / www.21cnjy.com / ) ( http: / / www.21cnjy.com / )
(1)求出A、P的坐标;
(2)求OB的长;
(3)如图2,点C在第一象限,,且,,动点M从点C出发,以每秒2个单位长度的速度向点B匀速运动,到达点B(无停留,速度保持不变)再沿射线BO匀速运动,动点N从点A出发,以每秒5个单位长度的速度沿射线AB方向匀速运动,点M、N同时出发,当的面积等于的面积的2倍时,求的面积.21*cnjy*com
5、长方形ABCD的长与宽分别是6和3,直接写出下列各图中A,B,C,D各个顶点的坐标.
( http: / / www.21cnjy.com / )
-参考答案-
一、单选题
1、D
【解析】
【分析】
根据确定位置的方法即可判断答案.
【详解】
A. 北偏东25°方向不能确定具体位置,缺少距离,故此选项错误;
B. 距学校800米处不能确定具体位置,缺少方向,故此选项错误;
C. 温州大剧院音乐厅8排不能确定具体位置,应具体到8排几号,故此选项错误;
D. 东经20°北纬30°可以确定一点的位置,故此选项正确.
故选:D.
【点睛】
本题考查确定位置的方法,掌握确定位置要具体到一点是解题的关键.
2、D
【解析】
【分析】
根据第四象限内横坐标大于零,纵坐标小于零,可得答案.
【详解】
解:点所在的象限是第四象限,
故选:D.
【点睛】
本题考查了点的坐标,熟记各象限内点的坐标特征是解题关键.
3、C
【解析】
【分析】
根据平面直角坐标系中点的坐标的表示方法求解即可.
【详解】
解:图中阴影区域是在第二象限,
A.(1,2)位于第一象限,故不在阴影区域内,不符合题意;
B.(-1,-2)位于第三象限,故不在阴影区域内,不符合题意;
C.(﹣1,2)位于第二象限,其横纵坐标的绝对值不超过3,故在阴影区域内,符合题意;
D. (1,-2)位于第四象限,故不在阴影区域内,不符合题意.
故选:C.
【点睛】
此题考查了平面直角坐标系中四个 ( http: / / www.21cnjy.com )象限中点的坐标特点,解题的关键是熟练掌握平面直角坐标系中四个象限中点的坐标特点:第一象限横坐标为正,纵坐标为正;第二象限横坐标为负,纵坐标为正;第三象限横坐标为负,纵坐标为负;第四象限横坐标为正,纵坐标为负.【来源:21·世纪·教育·网】
4、A
【解析】
【分析】
根据点到轴的距离是横坐标的绝对值,可得答案.
【详解】
解:∵,
∴点到轴的距离是
故选:A
【点睛】
本题考查的是点到坐标轴的距离,掌握点到轴的距离是横坐标的绝对值是解题的关键.
5、B
【解析】
【分析】
根据A、B两点的坐标建立平面直角坐标系即可得到C点坐标.
【详解】
解:∵A点坐标为(-2,-2),B点坐标为(4,-2),
∴可以建立如下图所示平面直角坐标系,
∴点C的坐标为(0,0),
故选B.
( http: / / www.21cnjy.com / )
【点睛】
本题主要考查了写出坐标系中点的坐标,解题的关键在于能够根据题意建立正确的平面直角坐标系.
6、D
【解析】
【分析】
根据各象限内点的坐标特征解答即可.
【详解】
解:点P(5,-5)的横坐标大于0,纵坐标小于0,所以点P所在的象限是第四象限.
故选:D.
【点睛】
本题考查了各象限内点的坐标的符号特征,记 ( http: / / www.21cnjy.com )住各象限内点的坐标的符号是解决的关键,四个象限的符号特点分别是:第一象限(+,+);第二象限(-,+);第三象限(-,-);第四象限(+,-).
7、A
【解析】
【分析】
根据y轴上点的横坐标为0列方程求解即可.
【详解】
解:∵点A(x+2,x﹣3)在y轴上,
∴x+2=0,
解得x=-2.
故选:A.
【点睛】
本题考查了点的坐标,熟记y轴上点的横坐标为0是解题的关键.
8、D
【解析】
【分析】
根据垂线段最短可知BC⊥l,即BC⊥x轴,由已知即可求解.
【详解】
解:∵点A(0,3),经过点A的直线l∥x轴,C是直线l上的一个动点,
∴点C的纵坐标是3,
根据垂线段最短可知,当BC⊥l时,线段BC的长度最短,此时, BC⊥x轴,
∵B(2,1),
∴点C的横坐标是2,
∴点C坐标为(2,3),
故选:D.
【点睛】
本题考查坐标与图形、垂线段最短,熟知图形与坐标的关系,掌握垂线段最短是解答的关键.
9、C
【解析】
【分析】
根据帅的位置,建立如图坐标系,并找出坐标对应的位置即可.
【详解】
解:如图,由(1,-2)表示帅的位置 ( http: / / www.21cnjy.com ),建立平面直角坐标系,帅的位置向上2个单位,向左1个单位为坐标原点,故由图可知(-2,1)上的棋子是炮的位置;21·cn·jy·com
( http: / / www.21cnjy.com / )
故选C.
【点睛】
本题考查了直角坐标系上点的位置的应用.解题的关键在于正确的建立平面直角坐标系.
10、A
【解析】
【分析】
根据平行及线段长度、点B在第二象限,可判断点B一定在点A的左侧,且两个点纵坐标相同,再由线段长即可确定点B的坐标.www.21-cn-jy.com
【详解】
解:∵轴,且,点B在第二象限,
∴点B一定在点A的左侧,且两个点纵坐标相同,
∴,即,
故选:A.
【点睛】
题目主要考查坐标系中点的坐标,理解题意,掌握坐标系中点的特征是解题关键.
二、填空题
1、3
【解析】
【分析】
根据点到x轴的距离等于纵坐标的绝对值解答即可.
【详解】
解:点A(4,﹣3)到x轴的距离是3.
故答案为:3.
【点睛】
本题考查点到坐标轴的距离,熟知点到坐标轴的距离与横(纵)坐标的关系是解答的关键.
2、
【解析】
【分析】
根据轴上点的横坐标为0,即可求得的值,进而代入即可求得点的坐标.
【详解】
解:在y轴上,
,
解得,
,
点M的坐标为.
故答案为:.
【点睛】
本题考查了点的坐标,熟知y轴上的点的横坐标为0是解答本题的关键.
3、一一对应
【解析】
略
4、 (4,4); (-2,-3); (4,-2)
【解析】
【分析】
用点坐标表示位置.
【详解】
①在直角坐标系中查横坐标为,纵坐标为;得到公园的位置为
故答案为:.
②在直角坐标系中查横坐标为,纵坐标为;得到车站的位置为
故答案为:.
③在直角坐标系中查横坐标为,纵坐标为;得到学校的位置为
故答案为:.
【点睛】
本题考察了坐标系中点的坐标.解题的关键在于正确的找出横、纵坐标的值.
5、
【解析】
【分析】
根据题中的规定,先算出,进而即可求解.
【详解】
解:∵,
∴
∵,
∴,
故答案为:.
【点睛】
本题考查了点的坐标,依据有关规定进行推理运算的能力,解答时注意按照从里向外依次求解.
三、解答题
1、(1)见解析;(2)见解析
【解析】
【分析】
先找到北偏东方向,再根据比例1∶10000,以1cm长度表示100m, 以学校为起点,作出2.6cm长的线段表示260米,即可得到少年宫的位置,同理找到南偏西45°方向,再以学校为起点作出3cm长的线段,即可得到公园的位置.21·世纪*教育网
【详解】
(1)如图,先找到北偏东方向,再根据比例1∶10000,以1cm长度表示100m, 以学校为起点,作出2.6cm长的线段表示260米,即可得到少年宫的位置;www-2-1-cnjy-com
(2)如图,同理找到南偏西45°方向,再以学校为起点作出3cm长的线段,即可得到公园的位置.
( http: / / www.21cnjy.com / )
【点睛】
本题考查了方位角和距离表示位置,掌握表示位置的方法是解题的关键.
2、答案不唯一.五个学生的位置分别为,,,,.
【解析】
【分析】
可在平面内任意一点为坐标原点建立平面直角坐标系,可以选取点A为坐标原点,建立平面直角坐标系,根据各点所在位置即可写成坐标.21*cnjy*com
【详解】
解:如图所示以点A为坐标原点建立的直角坐标系,这样,五个学生的位置的坐标分别为,,,,.根据建立的坐标原点不同,点坐标不同,为此答案不唯一.
( http: / / www.21cnjy.com / )
【点睛】
本题考查建立平面直角坐标系,写出点的坐标,掌握建立平面直角坐标系的方法,根据点的位置写出坐标是解题关键.【来源:21cnj*y.co*m】
3、(1)(4,1),(0,7),(4,0);(2)(0,0),(5,0),(3,2);(3)(0,4)
【解析】
【分析】
(1)据已知点的位置即可确定行列表示的数据的顺序,进而得出答案;
(2)据已知点的位置即可确定行列表示的数据的顺序,进而得出答案;
(3)画出图形,根据位置即可解答.
【详解】
解:(1)根据题意知棋子“帅”的位置可表示为(4,1),
棋子“黑车”的位置可表示为(0,7),
棋子“炮”的位置可表示为(5,0);
(2)根据题意知棋子“仕”的位置可表示为(0,0),
棋子“相”的位置可表示为(5,0),
棋子“黑马”的位置可表示为(3,2);
(3)A(0,0)点的位置如图所示:
( http: / / www.21cnjy.com / )
棋子“红马”的位置是(0,4).
【点睛】
本题主要考查了用有序实数对表示位置,正确得出行列表示的数据的顺序是解题关键.
4、 (1)A(8,0),P(-4, 9)
(2)6;
(3)24或60
【解析】
【分析】
(1)解方程组可求a, b的值,即可求解;
(2)由面积关系可求解;
(3)分两种情况讨论,由面积法可求OE的长,由面积关系可求解.
(1)
解:
解这个方程组得:
∴2a=2×4=8,-a=-4,3b=3×3=9,
∴A(8,0),P(-4, 9);
(2)
如图1,过点P作PH⊥x轴于H,连接BH,
( http: / / www.21cnjy.com / )
∵A(8,0),P(-4, 9),
∴OA=8,ОН=4,PH=9,
∴S△APH = S△ABH + SPHB ,
∴
∴OB=6;
(3)
设运动时间为ts,
∴BC=OВ,
∴BC= 4,
当0≤ t ≤2吋,如图2,过点O作OE⊥AB于 E,
( http: / / www.21cnjy.com / )
∴S△AOB=
∴
∴S△AON =
∴S△ABM=
∵△ AON的面积等于△ABM的面积的2倍,
∴12t=2 (12-6t),
∴t= 1,
∴S△PON = S△AOP-S△AON =;
当t > 2时,如图3,
( http: / / www.21cnjy.com / )
∴S△ABM= ,
∵△ AON的面积等于△ABM的面积的2倍,
∴12t=2×(8t- 16),
∴t= 8,
∴S△PON = S△AON-S△AOP =;
综上所述:△PON的面积为24或60.
【点睛】
本题考查了平面直角坐标系,三角形综合题,二元一次方程组的应用,三角形的面积公式,利用分类讨论思想解决问题是本题的关键.21世纪教育网版权所有
5、,,,.
【解析】
【分析】
根据长方形的长与宽的长度和长方形在坐标系中的位置即可求解.
【详解】
∵长方形ABCD的长与宽分别是6和3,
∴CD=6,AD=BC=3,
又由图可得,C在x轴负半轴上,D在x轴正半轴上,点A在第一象限,点B在第二象限,
∴,,,.
【点睛】
此题考查了坐标系中点的坐标表示,解题的关键是熟练掌握坐标系中点的坐标表示方法.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
七年级数学下册第14章位置与坐标单元测试
考试时间:90分钟;命题人:数学教研组
考生注意:
1、本卷分第I卷(选择题)和第Ⅱ卷(非选择题)两部分,满分100分,考试时间90分钟
2、答卷前,考生务必用0.5毫米黑色签字笔将自己的姓名、班级填写在试卷规定位置上
3、答案必须写在试卷各个题目指定区域 ( http: / / www.21cnjy.com )内相应的位置,如需改动,先划掉原来的答案,然后再写上新的答案;不准使用涂改液、胶带纸、修正带,不按以上要求作答的答案无效。21教育网
第I卷(选择题 30分)
一、单选题(10小题,每小题3分,共计30分)
1、根据下列表述,能够确定具体位置的是( )
A.北偏东25°方向 B.距学校800米处
C.温州大剧院音乐厅8排 D.东经20°北纬30°
2、在平面直角坐标系中,点所在的象限是( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
3、如图,每个小正方形的边长为1,在阴影区域的点是( )
( http: / / www.21cnjy.com / )
A.(1,2) B.(﹣1,﹣2) C.(﹣1,2) D.(1,﹣2)
4、平面直角坐标系中,点到y轴的距离是( )
A.1 B.2 C.3 D.4
5、如图,A、B两点的坐标分别为A(-2,-2)、B(4,-2),则点C的坐标为( )
( http: / / www.21cnjy.com / )
A.(2,2) B.(0,0) C.(0,2) D.(4,5)
6、在平面直角坐标系中,已知点P(5, 5),则点P在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
7、已知点A(x+2,x﹣3)在y轴上,则x的值为( )
A.﹣2 B.3 C.0 D.﹣3
8、在平面直角坐标系中,点 ( http: / / www.21cnjy.com )A(0,3),B(2,1),经过点A的直线l∥x轴,C是直线l上的一个动点,当线段BC的长度最短时,点C的坐标为( )21cnjy.com
A.(0,1) B.(2,0) C.(2,﹣1) D.(2,3)
9、如图是象棋棋盘的一部分,如果用(1,-2)表示帅的位置,那么点(-2,1)上的棋子是( )
( http: / / www.21cnjy.com / )
A.相 B.马 C.炮 D.兵
10、在平面直角坐标系中,点A的坐标为(﹣4,3),若AB∥x轴,且AB=5,当点B在第二象限时,点B的坐标是( )2·1·c·n·j·y
A.(﹣9,3) B.(﹣1,3) C.(1,﹣3) D.(1,3)
第Ⅱ卷(非选择题 70分)
二、填空题(5小题,每小题4分,共计20分)
1、在平面直角坐标系中,点A(4,﹣3)到x轴的距离是___.
2、在平面直角坐标系中,如果点在y轴上,那么点M的坐标是______.
3、平面上的点与坐标(有序实数对)是______的.
4、如图所示,公园的位置是_______,车站的位置是_______,学校的位置是_______.
( http: / / www.21cnjy.com / )
5、在平面直角坐标系中,对于平面内任一点,若规定以下两种变换:
(1).如:;
(2).如:;
按照以上变换有:,那么等于_______.
三、解答题(5小题,每小题10分,共计50分)
1、下面是比例尺为1∶10000的学校平面图,以学校为观测点,画一画.
( http: / / www.21cnjy.com / )
(1)少年宫在学校北偏东方向260米处.
(2)公园在学校南偏西方向300米处.
2、如图,五个学生正在做游戏,建立适当的直角坐标系,写出这五个学生所在位置的坐标.
( http: / / www.21cnjy.com / )
3、如图回答下列问题:
(1)如图①所示,请用有序数对写出棋盘上棋子“帅、黑车、炮”的位置(把列号写在前面,行号写在后面).2-1-c-n-j-y
(2)如图②所示把O点移动到棋子“仕”的位置时,用有序数对写出棋子“仕、相、黑马”的位置(把列号写在前面,行号写在后面)【出处:21教育名师】
(3)如图②,已知棋子“将”的位置是(2,8 ( http: / / www.21cnjy.com )),棋子“黑马”的位置是(4,3),规定列在前,行在后,请你在棋盘上确定A(0,0)点的位置,棋子“红马”的位置是什么? 【版权所有:21教育】
( http: / / www.21cnjy.com / )
4、如图1,在平面直角坐标系中,直线AB与x轴、y轴分别交于点A、B,点P在直线AB上,点A、P的坐标分别为,,且a、b是二元一次方程组的解.21教育名师原创作品
( http: / / www.21cnjy.com / ) ( http: / / www.21cnjy.com / )
(1)求出A、P的坐标;
(2)求OB的长;
(3)如图2,点C在第一象限,,且,,动点M从点C出发,以每秒2个单位长度的速度向点B匀速运动,到达点B(无停留,速度保持不变)再沿射线BO匀速运动,动点N从点A出发,以每秒5个单位长度的速度沿射线AB方向匀速运动,点M、N同时出发,当的面积等于的面积的2倍时,求的面积.21*cnjy*com
5、长方形ABCD的长与宽分别是6和3,直接写出下列各图中A,B,C,D各个顶点的坐标.
( http: / / www.21cnjy.com / )
-参考答案-
一、单选题
1、D
【解析】
【分析】
根据确定位置的方法即可判断答案.
【详解】
A. 北偏东25°方向不能确定具体位置,缺少距离,故此选项错误;
B. 距学校800米处不能确定具体位置,缺少方向,故此选项错误;
C. 温州大剧院音乐厅8排不能确定具体位置,应具体到8排几号,故此选项错误;
D. 东经20°北纬30°可以确定一点的位置,故此选项正确.
故选:D.
【点睛】
本题考查确定位置的方法,掌握确定位置要具体到一点是解题的关键.
2、D
【解析】
【分析】
根据第四象限内横坐标大于零,纵坐标小于零,可得答案.
【详解】
解:点所在的象限是第四象限,
故选:D.
【点睛】
本题考查了点的坐标,熟记各象限内点的坐标特征是解题关键.
3、C
【解析】
【分析】
根据平面直角坐标系中点的坐标的表示方法求解即可.
【详解】
解:图中阴影区域是在第二象限,
A.(1,2)位于第一象限,故不在阴影区域内,不符合题意;
B.(-1,-2)位于第三象限,故不在阴影区域内,不符合题意;
C.(﹣1,2)位于第二象限,其横纵坐标的绝对值不超过3,故在阴影区域内,符合题意;
D. (1,-2)位于第四象限,故不在阴影区域内,不符合题意.
故选:C.
【点睛】
此题考查了平面直角坐标系中四个 ( http: / / www.21cnjy.com )象限中点的坐标特点,解题的关键是熟练掌握平面直角坐标系中四个象限中点的坐标特点:第一象限横坐标为正,纵坐标为正;第二象限横坐标为负,纵坐标为正;第三象限横坐标为负,纵坐标为负;第四象限横坐标为正,纵坐标为负.【来源:21·世纪·教育·网】
4、A
【解析】
【分析】
根据点到轴的距离是横坐标的绝对值,可得答案.
【详解】
解:∵,
∴点到轴的距离是
故选:A
【点睛】
本题考查的是点到坐标轴的距离,掌握点到轴的距离是横坐标的绝对值是解题的关键.
5、B
【解析】
【分析】
根据A、B两点的坐标建立平面直角坐标系即可得到C点坐标.
【详解】
解:∵A点坐标为(-2,-2),B点坐标为(4,-2),
∴可以建立如下图所示平面直角坐标系,
∴点C的坐标为(0,0),
故选B.
( http: / / www.21cnjy.com / )
【点睛】
本题主要考查了写出坐标系中点的坐标,解题的关键在于能够根据题意建立正确的平面直角坐标系.
6、D
【解析】
【分析】
根据各象限内点的坐标特征解答即可.
【详解】
解:点P(5,-5)的横坐标大于0,纵坐标小于0,所以点P所在的象限是第四象限.
故选:D.
【点睛】
本题考查了各象限内点的坐标的符号特征,记 ( http: / / www.21cnjy.com )住各象限内点的坐标的符号是解决的关键,四个象限的符号特点分别是:第一象限(+,+);第二象限(-,+);第三象限(-,-);第四象限(+,-).
7、A
【解析】
【分析】
根据y轴上点的横坐标为0列方程求解即可.
【详解】
解:∵点A(x+2,x﹣3)在y轴上,
∴x+2=0,
解得x=-2.
故选:A.
【点睛】
本题考查了点的坐标,熟记y轴上点的横坐标为0是解题的关键.
8、D
【解析】
【分析】
根据垂线段最短可知BC⊥l,即BC⊥x轴,由已知即可求解.
【详解】
解:∵点A(0,3),经过点A的直线l∥x轴,C是直线l上的一个动点,
∴点C的纵坐标是3,
根据垂线段最短可知,当BC⊥l时,线段BC的长度最短,此时, BC⊥x轴,
∵B(2,1),
∴点C的横坐标是2,
∴点C坐标为(2,3),
故选:D.
【点睛】
本题考查坐标与图形、垂线段最短,熟知图形与坐标的关系,掌握垂线段最短是解答的关键.
9、C
【解析】
【分析】
根据帅的位置,建立如图坐标系,并找出坐标对应的位置即可.
【详解】
解:如图,由(1,-2)表示帅的位置 ( http: / / www.21cnjy.com ),建立平面直角坐标系,帅的位置向上2个单位,向左1个单位为坐标原点,故由图可知(-2,1)上的棋子是炮的位置;21·cn·jy·com
( http: / / www.21cnjy.com / )
故选C.
【点睛】
本题考查了直角坐标系上点的位置的应用.解题的关键在于正确的建立平面直角坐标系.
10、A
【解析】
【分析】
根据平行及线段长度、点B在第二象限,可判断点B一定在点A的左侧,且两个点纵坐标相同,再由线段长即可确定点B的坐标.www.21-cn-jy.com
【详解】
解:∵轴,且,点B在第二象限,
∴点B一定在点A的左侧,且两个点纵坐标相同,
∴,即,
故选:A.
【点睛】
题目主要考查坐标系中点的坐标,理解题意,掌握坐标系中点的特征是解题关键.
二、填空题
1、3
【解析】
【分析】
根据点到x轴的距离等于纵坐标的绝对值解答即可.
【详解】
解:点A(4,﹣3)到x轴的距离是3.
故答案为:3.
【点睛】
本题考查点到坐标轴的距离,熟知点到坐标轴的距离与横(纵)坐标的关系是解答的关键.
2、
【解析】
【分析】
根据轴上点的横坐标为0,即可求得的值,进而代入即可求得点的坐标.
【详解】
解:在y轴上,
,
解得,
,
点M的坐标为.
故答案为:.
【点睛】
本题考查了点的坐标,熟知y轴上的点的横坐标为0是解答本题的关键.
3、一一对应
【解析】
略
4、 (4,4); (-2,-3); (4,-2)
【解析】
【分析】
用点坐标表示位置.
【详解】
①在直角坐标系中查横坐标为,纵坐标为;得到公园的位置为
故答案为:.
②在直角坐标系中查横坐标为,纵坐标为;得到车站的位置为
故答案为:.
③在直角坐标系中查横坐标为,纵坐标为;得到学校的位置为
故答案为:.
【点睛】
本题考察了坐标系中点的坐标.解题的关键在于正确的找出横、纵坐标的值.
5、
【解析】
【分析】
根据题中的规定,先算出,进而即可求解.
【详解】
解:∵,
∴
∵,
∴,
故答案为:.
【点睛】
本题考查了点的坐标,依据有关规定进行推理运算的能力,解答时注意按照从里向外依次求解.
三、解答题
1、(1)见解析;(2)见解析
【解析】
【分析】
先找到北偏东方向,再根据比例1∶10000,以1cm长度表示100m, 以学校为起点,作出2.6cm长的线段表示260米,即可得到少年宫的位置,同理找到南偏西45°方向,再以学校为起点作出3cm长的线段,即可得到公园的位置.21·世纪*教育网
【详解】
(1)如图,先找到北偏东方向,再根据比例1∶10000,以1cm长度表示100m, 以学校为起点,作出2.6cm长的线段表示260米,即可得到少年宫的位置;www-2-1-cnjy-com
(2)如图,同理找到南偏西45°方向,再以学校为起点作出3cm长的线段,即可得到公园的位置.
( http: / / www.21cnjy.com / )
【点睛】
本题考查了方位角和距离表示位置,掌握表示位置的方法是解题的关键.
2、答案不唯一.五个学生的位置分别为,,,,.
【解析】
【分析】
可在平面内任意一点为坐标原点建立平面直角坐标系,可以选取点A为坐标原点,建立平面直角坐标系,根据各点所在位置即可写成坐标.21*cnjy*com
【详解】
解:如图所示以点A为坐标原点建立的直角坐标系,这样,五个学生的位置的坐标分别为,,,,.根据建立的坐标原点不同,点坐标不同,为此答案不唯一.
( http: / / www.21cnjy.com / )
【点睛】
本题考查建立平面直角坐标系,写出点的坐标,掌握建立平面直角坐标系的方法,根据点的位置写出坐标是解题关键.【来源:21cnj*y.co*m】
3、(1)(4,1),(0,7),(4,0);(2)(0,0),(5,0),(3,2);(3)(0,4)
【解析】
【分析】
(1)据已知点的位置即可确定行列表示的数据的顺序,进而得出答案;
(2)据已知点的位置即可确定行列表示的数据的顺序,进而得出答案;
(3)画出图形,根据位置即可解答.
【详解】
解:(1)根据题意知棋子“帅”的位置可表示为(4,1),
棋子“黑车”的位置可表示为(0,7),
棋子“炮”的位置可表示为(5,0);
(2)根据题意知棋子“仕”的位置可表示为(0,0),
棋子“相”的位置可表示为(5,0),
棋子“黑马”的位置可表示为(3,2);
(3)A(0,0)点的位置如图所示:
( http: / / www.21cnjy.com / )
棋子“红马”的位置是(0,4).
【点睛】
本题主要考查了用有序实数对表示位置,正确得出行列表示的数据的顺序是解题关键.
4、 (1)A(8,0),P(-4, 9)
(2)6;
(3)24或60
【解析】
【分析】
(1)解方程组可求a, b的值,即可求解;
(2)由面积关系可求解;
(3)分两种情况讨论,由面积法可求OE的长,由面积关系可求解.
(1)
解:
解这个方程组得:
∴2a=2×4=8,-a=-4,3b=3×3=9,
∴A(8,0),P(-4, 9);
(2)
如图1,过点P作PH⊥x轴于H,连接BH,
( http: / / www.21cnjy.com / )
∵A(8,0),P(-4, 9),
∴OA=8,ОН=4,PH=9,
∴S△APH = S△ABH + SPHB ,
∴
∴OB=6;
(3)
设运动时间为ts,
∴BC=OВ,
∴BC= 4,
当0≤ t ≤2吋,如图2,过点O作OE⊥AB于 E,
( http: / / www.21cnjy.com / )
∴S△AOB=
∴
∴S△AON =
∴S△ABM=
∵△ AON的面积等于△ABM的面积的2倍,
∴12t=2 (12-6t),
∴t= 1,
∴S△PON = S△AOP-S△AON =;
当t > 2时,如图3,
( http: / / www.21cnjy.com / )
∴S△ABM= ,
∵△ AON的面积等于△ABM的面积的2倍,
∴12t=2×(8t- 16),
∴t= 8,
∴S△PON = S△AON-S△AOP =;
综上所述:△PON的面积为24或60.
【点睛】
本题考查了平面直角坐标系,三角形综合题,二元一次方程组的应用,三角形的面积公式,利用分类讨论思想解决问题是本题的关键.21世纪教育网版权所有
5、,,,.
【解析】
【分析】
根据长方形的长与宽的长度和长方形在坐标系中的位置即可求解.
【详解】
∵长方形ABCD的长与宽分别是6和3,
∴CD=6,AD=BC=3,
又由图可得,C在x轴负半轴上,D在x轴正半轴上,点A在第一象限,点B在第二象限,
∴,,,.
【点睛】
此题考查了坐标系中点的坐标表示,解题的关键是熟练掌握坐标系中点的坐标表示方法.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
- 第8章 角
- 8.1 角的表示
- 8.2 角的比较
- 8.3 角的度量
- 8.4 对顶角
- 8.5 垂直
- 第9章 平行线
- 9.1 同位角、内错角、同旁内角
- 9.2 平行线和它的画法
- 9.3 平行线的性质
- 9.4 平行线的判定
- 第10章 一次方程组
- 10.1 认识二元一次方程组
- 10.2 二元一次方程组的解法
- 10.3 三元一次方程组
- 10.4 列方程组解应用题
- 第11章 整式的乘除
- 11.1 同底数幂的乘法
- 11.2 积的乘方与幂的乘方
- 11.3 单项式的乘法
- 11.4 多项式乘多项式
- 11.5 同底数幂的除法
- 11.6 零指数幂与负整数指数幂
- 第12章 乘法公式与因式分解
- 12.1 平方差公式
- 12.2 完全平方公式
- 12.3 用提公因式法进行因式分解
- 12.4 用公式法进行因式分解
- 第13章 平面图形的认识
- 13.1 三角形
- 13.2 多边形
- 13.3 圆
- 第14章 位置与坐标
- 14.1 用有序数对表示位置
- 14.2 平面直角坐标系
- 14.3 直角坐标系中的图形
- 14.4 用方向和距离描述两个物体的相对位置
