第一章 勾股定理微专题1 利用勾股定理解决折叠与展开问题 北师大版数学八年级上册微专题(含答案)
文档属性
| 名称 | 第一章 勾股定理微专题1 利用勾股定理解决折叠与展开问题 北师大版数学八年级上册微专题(含答案) |
|
|
| 格式 | doc | ||
| 文件大小 | 454.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-25 00:00:00 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
北师大版数学八年级上册微专题
微专题1 利用勾股定理解决折叠与展开问题
类型一 利用勾股定理解决平面图形的折叠问题
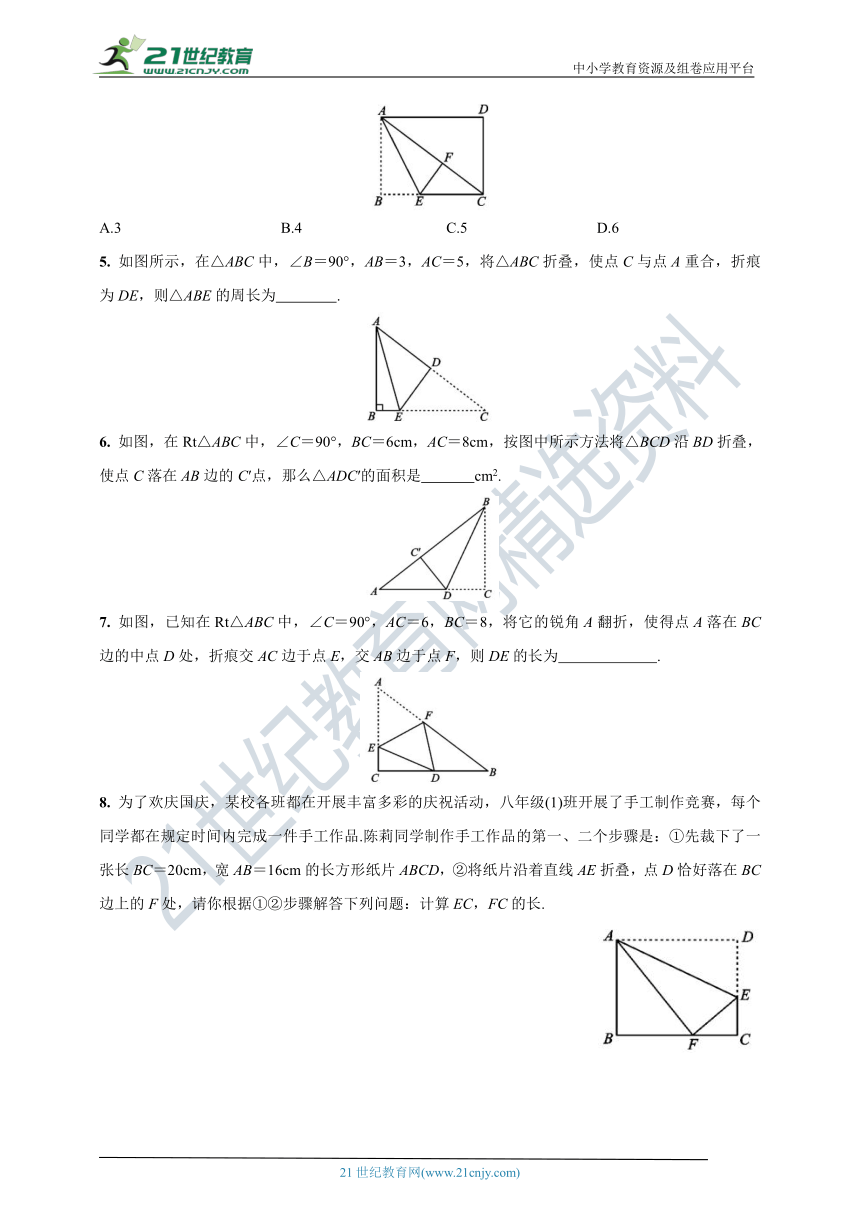
1. 如图所示,有一块直角三角形纸片,∠C=90°,AC=4cm,BC=3cm,将斜边AB翻折,使点B落在直角边AC的延长线上的点E处,折痕为AD,则CE的长为( )
A.1cm B.1.5cm C.2cm D.3cm
2. 如图,有一张直角三角形纸片,两直角边AC=5cm,BC=10cm,将△ABC折叠,使点B与点A重合,折痕为DE,则CD的长为( )
A.cm B. cm C.cm D.cm
3. 如图,将长方形纸片ABCD沿直线EF折叠,使点C落在AD边的中点C′处,点B落在点B′处,其中AB=9,BC=6,则FC′的长为( )
A. B.4 C. D.5
4. 如图,长方形纸片ABCD中,已知AD=8,折叠纸片使AB边与对角线AC重合,点B落在点F处,折痕为AE,且EF=3,则AB的长为( )
A.3 B.4 C.5 D.6
5. 如图所示,在△ABC中,∠B=90°,AB=3,AC=5,将△ABC折叠,使点C与点A重合,折痕为DE,则△ABE的周长为 .
6. 如图,在Rt△ABC中,∠C=90°,BC=6cm,AC=8cm,按图中所示方法将△BCD沿BD折叠,使点C落在AB边的C′点,那么△ADC′的面积是 cm2.
7. 如图,已知在Rt△ABC中,∠C=90°,AC=6,BC=8,将它的锐角A翻折,使得点A落在BC边的中点D处,折痕交AC边于点E,交AB边于点F,则DE的长为 .
8. 为了欢庆国庆,某校各班都在开展丰富多彩的庆祝活动,八年级(1)班开展了手工制作竞赛,每个同学都在规定时间内完成一件手工作品.陈莉同学制作手工作品的第一、二个步骤是:①先裁下了一张长BC=20cm,宽AB=16cm的长方形纸片ABCD,②将纸片沿着直线AE折叠,点D恰好落在BC边上的F处,请你根据①②步骤解答下列问题:计算EC,FC的长.
类型二 利用勾股定理解决立体图形的展开问题
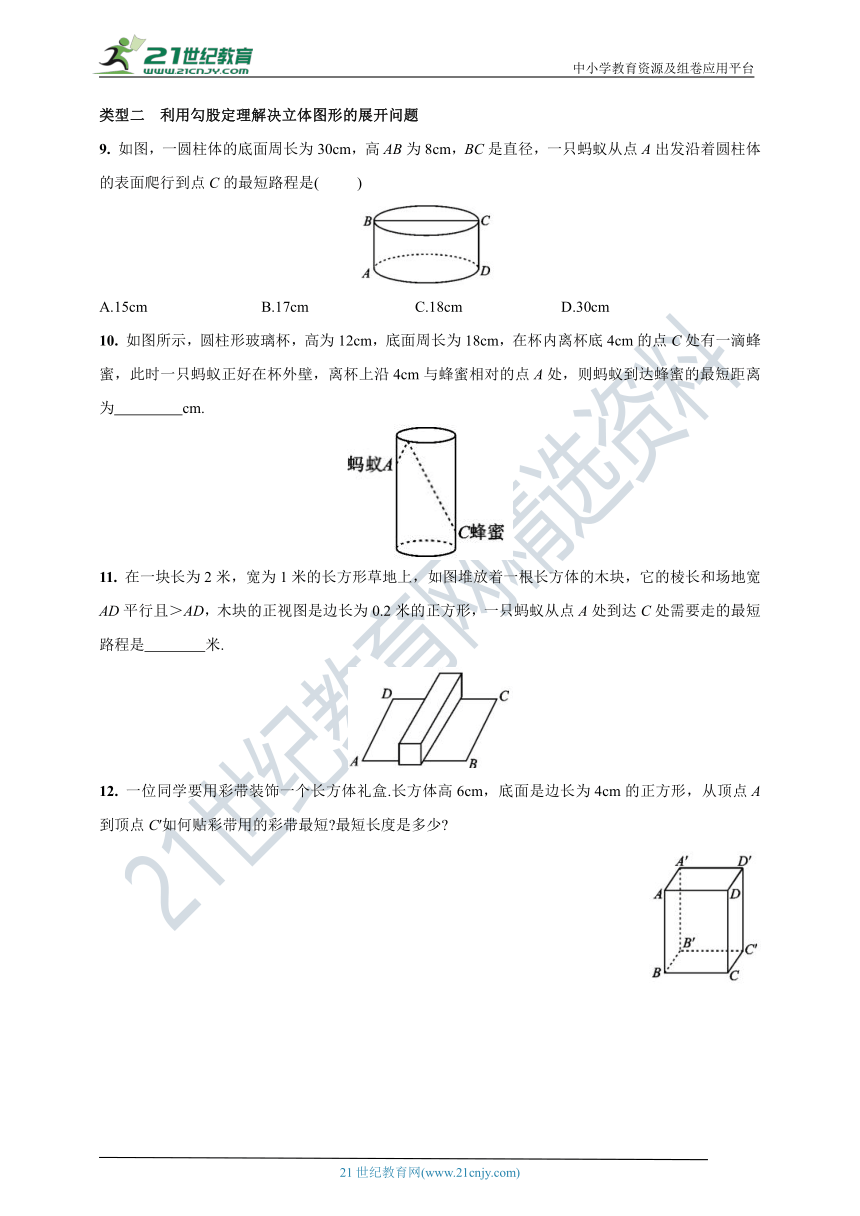
9. 如图,一圆柱体的底面周长为30cm,高AB为8cm,BC是直径,一只蚂蚁从点A出发沿着圆柱体的表面爬行到点C的最短路程是( )
A.15cm B.17cm C.18cm D.30cm
10. 如图所示,圆柱形玻璃杯,高为12cm,底面周长为18cm,在杯内离杯底4cm的点C处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿4cm与蜂蜜相对的点A处,则蚂蚁到达蜂蜜的最短距离为 cm.
11. 在一块长为2米,宽为1米的长方形草地上,如图堆放着一根长方体的木块,它的棱长和场地宽AD平行且>AD,木块的正视图是边长为0.2米的正方形,一只蚂蚁从点A处到达C处需要走的最短路程是 米.
12. 一位同学要用彩带装饰一个长方体礼盒.长方体高6cm,底面是边长为4cm的正方形,从顶点A到顶点C′如何贴彩带用的彩带最短 最短长度是多少
13. 我国古代有这样一道数学问题:“枯木一根直立地上,高二丈,周三尺,有葛藤自根缠绕而上,五周而达其顶,问葛藤之长几何 ”题意是:如图所示,把枯木看作一个圆柱体,因一丈是十尺,则该圆柱的高为20尺,底面周长为3尺,有葛藤自点A处缠绕而上,绕五周后其末端恰好到达点B处,求问题中葛藤的最短长度.
14. 如图,一个长方体形状的木柜放在墙角处(与墙面和地面均没有缝隙),有一只蚂蚁从柜角A处沿着木柜表面爬到柜角C1处.
(1)请你画出蚂蚁能够最快到达目的地的可能路径;
(2)当AB=4,BC=4,CC1=5时,求蚂蚁爬过的最短路径的长的平方.
参 考 答 案
1. A 2. D 3. D 4. D
5. 7 6. 6 7.
8. 解:因为△ADE与△AFE关于AE对称,所以△ADE≌△AFE.所以DE=FE,AD=AF.因为BC=20cm,AB=16cm,所以CD=16cm,AD=AF=20cm. 在Rt△ABF中,由勾股定理得BF=12cm. 所以FC=20-12=8cm. 因为四边形ABCD是长方形,所以∠C=90°. 设CE=x,则DE=EF=16-x,在Rt△CEF中,由勾股定理得(16-x)2=64+x2. 解得x=6. 所以EC=6cm. 即EC=6cm,FC=8cm.
9. B
10. 15 11. 2.6
12. 解:把长方体的面DCC′D′沿棱C′D′展开至面ABCD上,如图.构成长方形ABC′D′,则点A到点C′的最短距离为AC′的长度,连接AC′交DC于点O,易证△AOD≌△C′OC.∴OD=OC.即O为DC的中点,由勾股定理,得AC′2=AD′2+D′C′2=82+62=100,∴AC′=10cm. 即从顶点A沿直线到DC中点O,再沿直线到顶点C′,贴的彩带最短,最短长度为10cm.
13. 解:展开后如图,∵BC=20尺,AC=5×3=15(尺),在Rt△ABC中,由勾股定理,得AB2=AC2+BC2=152+202=625,∴AB=25尺. 答:葛藤的最短长度为25尺.
14. 解:(1)如图,木柜的表面展开图是两个长方形ABC1′D1和ACC1A1. 蚂蚁能够最快到达目的地的可能路径有如图所示的AC1′和AC1两种.
(2)①蚂蚁沿着木柜表面经线段A1B1到C′1,设爬过的路径的长为l1,则l12=42+(4+5)2=97;
②蚂蚁沿着木柜表面经线段BB1到C1,设爬过的路径的长为l2,则l22=52+(4+4)2=89. ∵l12>l22,∴最短路径的长的平方是89.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
北师大版数学八年级上册微专题
微专题1 利用勾股定理解决折叠与展开问题
类型一 利用勾股定理解决平面图形的折叠问题
1. 如图所示,有一块直角三角形纸片,∠C=90°,AC=4cm,BC=3cm,将斜边AB翻折,使点B落在直角边AC的延长线上的点E处,折痕为AD,则CE的长为( )
A.1cm B.1.5cm C.2cm D.3cm
2. 如图,有一张直角三角形纸片,两直角边AC=5cm,BC=10cm,将△ABC折叠,使点B与点A重合,折痕为DE,则CD的长为( )
A.cm B. cm C.cm D.cm
3. 如图,将长方形纸片ABCD沿直线EF折叠,使点C落在AD边的中点C′处,点B落在点B′处,其中AB=9,BC=6,则FC′的长为( )
A. B.4 C. D.5
4. 如图,长方形纸片ABCD中,已知AD=8,折叠纸片使AB边与对角线AC重合,点B落在点F处,折痕为AE,且EF=3,则AB的长为( )
A.3 B.4 C.5 D.6
5. 如图所示,在△ABC中,∠B=90°,AB=3,AC=5,将△ABC折叠,使点C与点A重合,折痕为DE,则△ABE的周长为 .
6. 如图,在Rt△ABC中,∠C=90°,BC=6cm,AC=8cm,按图中所示方法将△BCD沿BD折叠,使点C落在AB边的C′点,那么△ADC′的面积是 cm2.
7. 如图,已知在Rt△ABC中,∠C=90°,AC=6,BC=8,将它的锐角A翻折,使得点A落在BC边的中点D处,折痕交AC边于点E,交AB边于点F,则DE的长为 .
8. 为了欢庆国庆,某校各班都在开展丰富多彩的庆祝活动,八年级(1)班开展了手工制作竞赛,每个同学都在规定时间内完成一件手工作品.陈莉同学制作手工作品的第一、二个步骤是:①先裁下了一张长BC=20cm,宽AB=16cm的长方形纸片ABCD,②将纸片沿着直线AE折叠,点D恰好落在BC边上的F处,请你根据①②步骤解答下列问题:计算EC,FC的长.
类型二 利用勾股定理解决立体图形的展开问题
9. 如图,一圆柱体的底面周长为30cm,高AB为8cm,BC是直径,一只蚂蚁从点A出发沿着圆柱体的表面爬行到点C的最短路程是( )
A.15cm B.17cm C.18cm D.30cm
10. 如图所示,圆柱形玻璃杯,高为12cm,底面周长为18cm,在杯内离杯底4cm的点C处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿4cm与蜂蜜相对的点A处,则蚂蚁到达蜂蜜的最短距离为 cm.
11. 在一块长为2米,宽为1米的长方形草地上,如图堆放着一根长方体的木块,它的棱长和场地宽AD平行且>AD,木块的正视图是边长为0.2米的正方形,一只蚂蚁从点A处到达C处需要走的最短路程是 米.
12. 一位同学要用彩带装饰一个长方体礼盒.长方体高6cm,底面是边长为4cm的正方形,从顶点A到顶点C′如何贴彩带用的彩带最短 最短长度是多少
13. 我国古代有这样一道数学问题:“枯木一根直立地上,高二丈,周三尺,有葛藤自根缠绕而上,五周而达其顶,问葛藤之长几何 ”题意是:如图所示,把枯木看作一个圆柱体,因一丈是十尺,则该圆柱的高为20尺,底面周长为3尺,有葛藤自点A处缠绕而上,绕五周后其末端恰好到达点B处,求问题中葛藤的最短长度.
14. 如图,一个长方体形状的木柜放在墙角处(与墙面和地面均没有缝隙),有一只蚂蚁从柜角A处沿着木柜表面爬到柜角C1处.
(1)请你画出蚂蚁能够最快到达目的地的可能路径;
(2)当AB=4,BC=4,CC1=5时,求蚂蚁爬过的最短路径的长的平方.
参 考 答 案
1. A 2. D 3. D 4. D
5. 7 6. 6 7.
8. 解:因为△ADE与△AFE关于AE对称,所以△ADE≌△AFE.所以DE=FE,AD=AF.因为BC=20cm,AB=16cm,所以CD=16cm,AD=AF=20cm. 在Rt△ABF中,由勾股定理得BF=12cm. 所以FC=20-12=8cm. 因为四边形ABCD是长方形,所以∠C=90°. 设CE=x,则DE=EF=16-x,在Rt△CEF中,由勾股定理得(16-x)2=64+x2. 解得x=6. 所以EC=6cm. 即EC=6cm,FC=8cm.
9. B
10. 15 11. 2.6
12. 解:把长方体的面DCC′D′沿棱C′D′展开至面ABCD上,如图.构成长方形ABC′D′,则点A到点C′的最短距离为AC′的长度,连接AC′交DC于点O,易证△AOD≌△C′OC.∴OD=OC.即O为DC的中点,由勾股定理,得AC′2=AD′2+D′C′2=82+62=100,∴AC′=10cm. 即从顶点A沿直线到DC中点O,再沿直线到顶点C′,贴的彩带最短,最短长度为10cm.
13. 解:展开后如图,∵BC=20尺,AC=5×3=15(尺),在Rt△ABC中,由勾股定理,得AB2=AC2+BC2=152+202=625,∴AB=25尺. 答:葛藤的最短长度为25尺.
14. 解:(1)如图,木柜的表面展开图是两个长方形ABC1′D1和ACC1A1. 蚂蚁能够最快到达目的地的可能路径有如图所示的AC1′和AC1两种.
(2)①蚂蚁沿着木柜表面经线段A1B1到C′1,设爬过的路径的长为l1,则l12=42+(4+5)2=97;
②蚂蚁沿着木柜表面经线段BB1到C1,设爬过的路径的长为l2,则l22=52+(4+4)2=89. ∵l12>l22,∴最短路径的长的平方是89.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
