第一章 勾股定理综合强化练 1.1-1.3 北师大版数学八年级上册综合强化练(含答案)
文档属性
| 名称 | 第一章 勾股定理综合强化练 1.1-1.3 北师大版数学八年级上册综合强化练(含答案) | 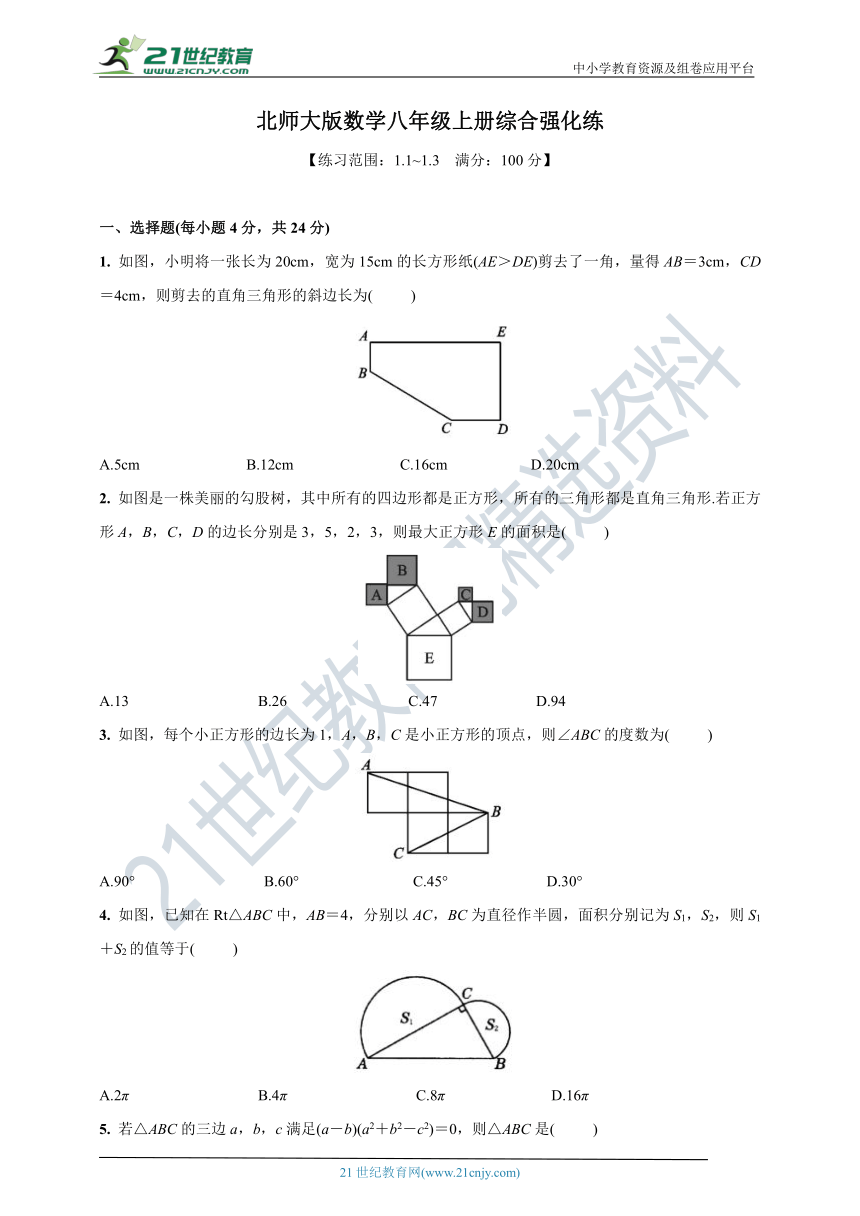 | |
| 格式 | doc | ||
| 文件大小 | 408.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-25 15:52:10 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
北师大版数学八年级上册综合强化练
【练习范围:1.1~1.3 满分:100分】
一、选择题(每小题4分,共24分)
1. 如图,小明将一张长为20cm,宽为15cm的长方形纸(AE>DE)剪去了一角,量得AB=3cm,CD=4cm,则剪去的直角三角形的斜边长为( )
A.5cm B.12cm C.16cm D.20cm
2. 如图是一株美丽的勾股树,其中所有的四边形都是正方形,所有的三角形都是直角三角形.若正方形A,B,C,D的边长分别是3,5,2,3,则最大正方形E的面积是( )
A.13 B.26 C.47 D.94
3. 如图,每个小正方形的边长为1,A,B,C是小正方形的顶点,则∠ABC的度数为( )
A.90° B.60° C.45° D.30°
4. 如图,已知在Rt△ABC中,AB=4,分别以AC,BC为直径作半圆,面积分别记为S1,S2,则S1+S2的值等于( )
A.2π B.4π C.8π D.16π
5. 若△ABC的三边a,b,c满足(a-b)(a2+b2-c2)=0,则△ABC是( )
A.等腰三角形 B.直角三角形
C.等边三角形 D.等腰三角形或直角三角形
6. 如图,直线l上有三个正方形a,b,c,若a,c的面积分别为3和4,则b的面积为( )
A.16 B.12 C.9 D.7
二、填空题(每小题4分,共24分)
7. 一个三角形的三边之比为5∶12∶13,且周长为60cm,则它的面积是 .
8. 如果一个三角形有两边的平方分别为16,25,那么第三边的平方是 时,这个三角形是直角三角形.
9. 如图,要制作底边BC的长为40cm,顶点A到BC的距离与BC长的比为3∶8的等腰三角形木衣架,则腰AB的长至少需要 cm.
10. 如图所示,一圆柱高4m,底面周长为6m,现需按如图方式缠绕一圈彩带进行装饰,则腰带最短要用 m.
11. 如图,已知长方形纸片ABCD的边长AB=4,AD=2. 将长方形纸片沿EF折叠,使点A与点C重合,折叠后在其一面涂色,则涂色部分的面积为 .
12. 有诗曰:“平地秋千未起,踏板一尺离地.送行二步与人齐,五尺人高曾记.仕女佳人争蹴,终朝笑语欢嬉.良工高士好奇,算出索长有几 ”意思是:秋千静挂时,踏板离地的高度是1尺.现在晃出两步的距离,有人记录踏板离地的高度为5尺.仕女佳人争着荡秋千,一整天都欢声笑语,工匠师傅们好奇的是秋千绳索有多长呢 (注:一步合五尺),则秋千绳索的长度为 尺.
三、解答题(共52分)
13. (12分)如图,每个小方格都是边长为1的正方形,求:
(1)四边形ABCD的面积;
(2)∠ABC的度数.
14. (12分)如图,将长方形ABCD沿直线BD折叠,使点C落在点C′处,BC′交AD于E,AD=8,AB=4,求△BED的面积.
15. (14分)如图,一个长方体纸盒,它的长、宽、高分别为8,4,5,在盒内顶点A处有一只壁虎,它发现盒内其对角顶点B处有一只苍蝇,于是壁虎向点B爬行,求这只壁虎由点A爬行至点B的最短路径长的平方.
16. (14分)如图,点E是正方形ABCD内一点,连接AE,BE,CE,将△ABE绕点B顺时针旋转90°到△CBE′的位置.若AE=1,BE=2,CE=3,求∠BE′C的度数.
参 考 答 案
1. D 2. C 3. C 4. A 5. D 6. D
7. 120cm2 8. 9或41 9. 25 10. 10 11. 12. 14.5
13. 解:(1)S四边形ABCD=S△ABC+S△ACD=×5×2+×5×3=;
(2)因为AB2=22+42=20,BC2=12+22=5,AC2=52=25,所以AB2+BC2=AC2,所以∠ABC=90°.
14. 解:由折叠可得∠1=∠2,∵AD∥BC,∴∠2=∠3,∴∠1=∠3,∴BE=DE,设BE=x,则DE=x,AE=8-x. 在Rt△ABE中,由勾股定理,得AB2+AE2=BE2,∴42+(8-x)2=x2,解得x=5. ∴S△BED=DE·AB=×5×4=10.
15. 解:如图,将涉及点A和点B的两个相邻的面展开:
由勾股定理可知:图①中AB2=(4+8)2+52=169,图②中AB2=(5+4)2+82=145,图③中AB2=(8+5)2+42=185,∵185>169>145,∴最短路径长的平方为145.
16. 解:连接EE′,由旋转得△ABE≌△CBE′,∴AE=CE′=1,BE=BE′=2,∠ABE=∠CBE′. ∵∠ABC=90°,∴∠EBE′=90°. 在Rt△EBE′中,由勾股定理,得EE′2=BE2+BE′2=8,又∵BE=BE′,∴∠BE′E=45°,∵EC=3,E′C=1,E′C2+EE′2=EC2,∴∠EE′C=90°,∴∠BE′C=∠BE′E+∠EE′C=135°.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
北师大版数学八年级上册综合强化练
【练习范围:1.1~1.3 满分:100分】
一、选择题(每小题4分,共24分)
1. 如图,小明将一张长为20cm,宽为15cm的长方形纸(AE>DE)剪去了一角,量得AB=3cm,CD=4cm,则剪去的直角三角形的斜边长为( )
A.5cm B.12cm C.16cm D.20cm
2. 如图是一株美丽的勾股树,其中所有的四边形都是正方形,所有的三角形都是直角三角形.若正方形A,B,C,D的边长分别是3,5,2,3,则最大正方形E的面积是( )
A.13 B.26 C.47 D.94
3. 如图,每个小正方形的边长为1,A,B,C是小正方形的顶点,则∠ABC的度数为( )
A.90° B.60° C.45° D.30°
4. 如图,已知在Rt△ABC中,AB=4,分别以AC,BC为直径作半圆,面积分别记为S1,S2,则S1+S2的值等于( )
A.2π B.4π C.8π D.16π
5. 若△ABC的三边a,b,c满足(a-b)(a2+b2-c2)=0,则△ABC是( )
A.等腰三角形 B.直角三角形
C.等边三角形 D.等腰三角形或直角三角形
6. 如图,直线l上有三个正方形a,b,c,若a,c的面积分别为3和4,则b的面积为( )
A.16 B.12 C.9 D.7
二、填空题(每小题4分,共24分)
7. 一个三角形的三边之比为5∶12∶13,且周长为60cm,则它的面积是 .
8. 如果一个三角形有两边的平方分别为16,25,那么第三边的平方是 时,这个三角形是直角三角形.
9. 如图,要制作底边BC的长为40cm,顶点A到BC的距离与BC长的比为3∶8的等腰三角形木衣架,则腰AB的长至少需要 cm.
10. 如图所示,一圆柱高4m,底面周长为6m,现需按如图方式缠绕一圈彩带进行装饰,则腰带最短要用 m.
11. 如图,已知长方形纸片ABCD的边长AB=4,AD=2. 将长方形纸片沿EF折叠,使点A与点C重合,折叠后在其一面涂色,则涂色部分的面积为 .
12. 有诗曰:“平地秋千未起,踏板一尺离地.送行二步与人齐,五尺人高曾记.仕女佳人争蹴,终朝笑语欢嬉.良工高士好奇,算出索长有几 ”意思是:秋千静挂时,踏板离地的高度是1尺.现在晃出两步的距离,有人记录踏板离地的高度为5尺.仕女佳人争着荡秋千,一整天都欢声笑语,工匠师傅们好奇的是秋千绳索有多长呢 (注:一步合五尺),则秋千绳索的长度为 尺.
三、解答题(共52分)
13. (12分)如图,每个小方格都是边长为1的正方形,求:
(1)四边形ABCD的面积;
(2)∠ABC的度数.
14. (12分)如图,将长方形ABCD沿直线BD折叠,使点C落在点C′处,BC′交AD于E,AD=8,AB=4,求△BED的面积.
15. (14分)如图,一个长方体纸盒,它的长、宽、高分别为8,4,5,在盒内顶点A处有一只壁虎,它发现盒内其对角顶点B处有一只苍蝇,于是壁虎向点B爬行,求这只壁虎由点A爬行至点B的最短路径长的平方.
16. (14分)如图,点E是正方形ABCD内一点,连接AE,BE,CE,将△ABE绕点B顺时针旋转90°到△CBE′的位置.若AE=1,BE=2,CE=3,求∠BE′C的度数.
参 考 答 案
1. D 2. C 3. C 4. A 5. D 6. D
7. 120cm2 8. 9或41 9. 25 10. 10 11. 12. 14.5
13. 解:(1)S四边形ABCD=S△ABC+S△ACD=×5×2+×5×3=;
(2)因为AB2=22+42=20,BC2=12+22=5,AC2=52=25,所以AB2+BC2=AC2,所以∠ABC=90°.
14. 解:由折叠可得∠1=∠2,∵AD∥BC,∴∠2=∠3,∴∠1=∠3,∴BE=DE,设BE=x,则DE=x,AE=8-x. 在Rt△ABE中,由勾股定理,得AB2+AE2=BE2,∴42+(8-x)2=x2,解得x=5. ∴S△BED=DE·AB=×5×4=10.
15. 解:如图,将涉及点A和点B的两个相邻的面展开:
由勾股定理可知:图①中AB2=(4+8)2+52=169,图②中AB2=(5+4)2+82=145,图③中AB2=(8+5)2+42=185,∵185>169>145,∴最短路径长的平方为145.
16. 解:连接EE′,由旋转得△ABE≌△CBE′,∴AE=CE′=1,BE=BE′=2,∠ABE=∠CBE′. ∵∠ABC=90°,∴∠EBE′=90°. 在Rt△EBE′中,由勾股定理,得EE′2=BE2+BE′2=8,又∵BE=BE′,∴∠BE′E=45°,∵EC=3,E′C=1,E′C2+EE′2=EC2,∴∠EE′C=90°,∴∠BE′C=∠BE′E+∠EE′C=135°.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
