北师大版数学六年级上册单元测试卷 第三单元 观察物体(含答案)
文档属性
| 名称 | 北师大版数学六年级上册单元测试卷 第三单元 观察物体(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 370.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-17 10:27:57 | ||
图片预览


文档简介
保密★启用前
北师大版数学六年级上册单元测试卷
第三单元 观察物体
学校:___________姓名:___________班级:___________考号:___________
题号 一 二 三 四 五 六 总分
得分
一、选择题
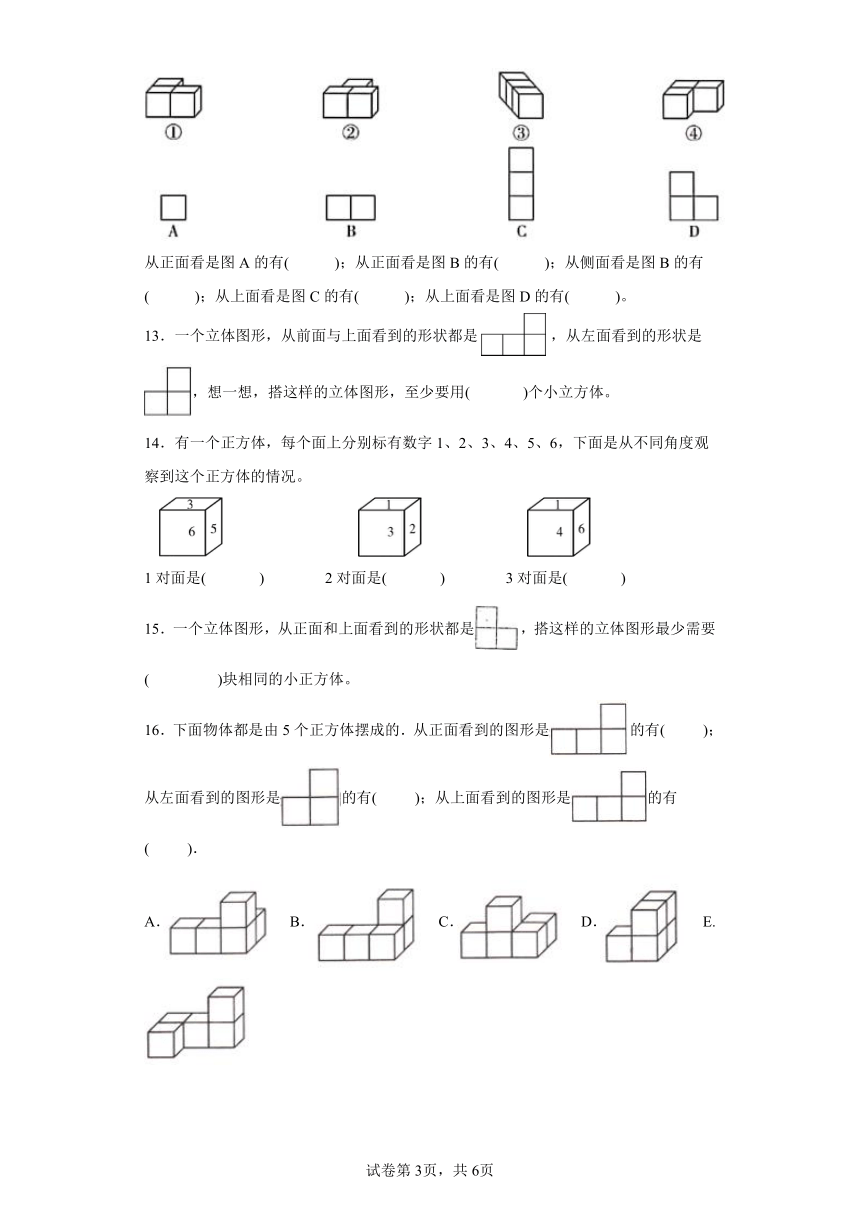
1.用同样大小的正方体摆成物体(两个正方体之间至少有一个面重叠),从正面看到的是,从上面看到的是,从左面看到的是( )。
A. B. C. D.无法确定
2.如图,搭出同时符合下面要求的几何体,需要( )个小正方体。
A.3 B.4 C.5 D.6
3.下列关于观察物体的说法,错误的是( )。
A.成语“登高望远”是指站得越高,观察到的范围越大。
B.晚上散步时如果逐渐向路灯走近,影子就会逐渐变长。
C.站在两个不同方向拍同一建筑物,拍出的照片有可能是一样的。
4.用大小相同的小正方体搭成一个立体图形,从正面看到的形状是,从上面看到的形状是,从右面看到的形状是( )。
A. B. C. D.
5.从正面观察下面的立体图形,看到的形状是( )。
A. B. C.
6.“欲穷千里目,更上一层楼”用数学的知识解释是站得越高,看到的范围( )。
A.越小 B.越大 C.不变 D.没有变化
7.用4个同样大小的正方体摆成的形状,从正面看是,从上面看是,从左面看是( )。
A. B. C.
8.在下面的4个几何体中,从左面看到形状是的图形是( )。
A. B.
C. D.
二、填空题
9.如图,某学校在教学楼安装摄像头,安装在( )点监控到地面的范围最大。
10.一个立体图形,从右面看到的形状是,从上面看到的形状是,搭这样的一个立体图形,最少需要( )个小方体,最多可以用( )个小立方体。
11.如图,从( )面看到的形状是,从( )面看到的形状是。
12.分一分,填一填。(填序号)
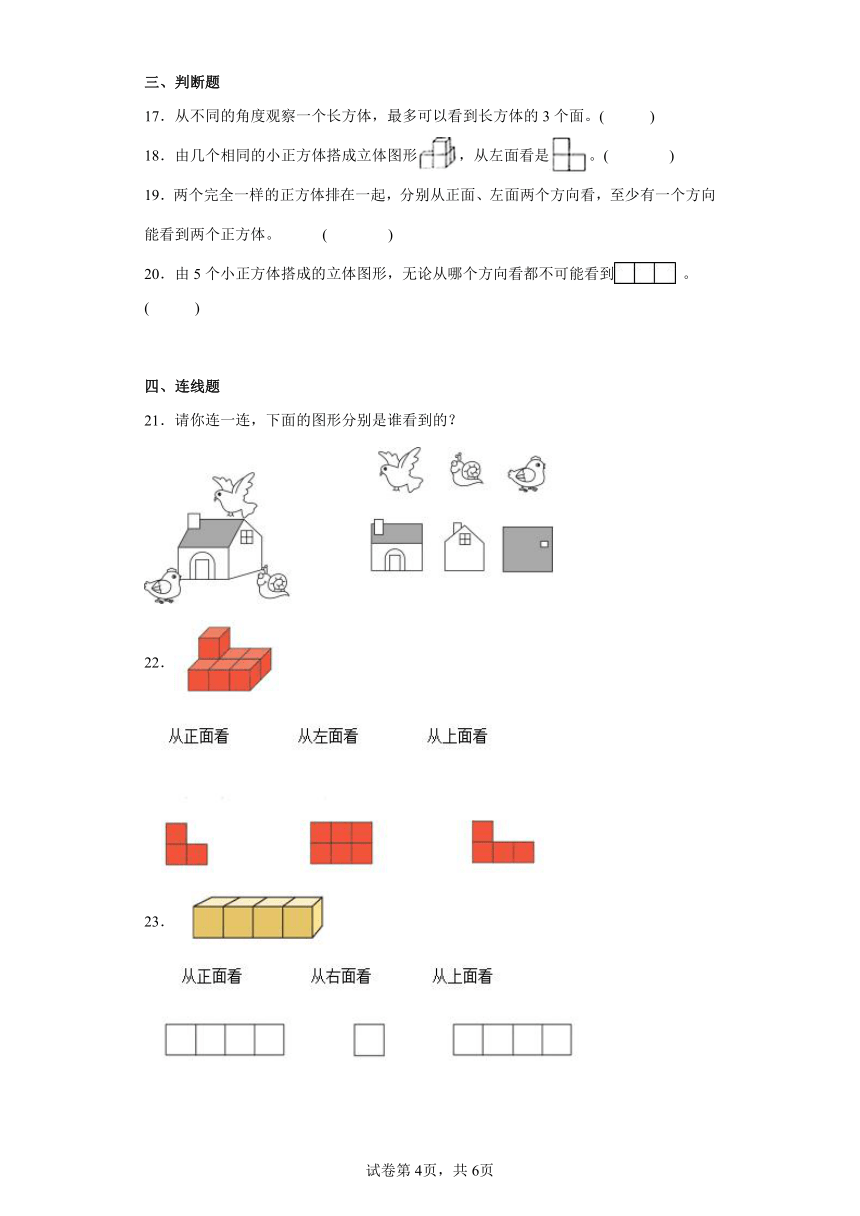
从正面看是图A的有( );从正面看是图B的有( );从侧面看是图B的有( );从上面看是图C的有( );从上面看是图D的有( )。
13.一个立体图形,从前面与上面看到的形状都是 ,从左面看到的形状是,想一想,搭这样的立体图形,至少要用( )个小立方体。
14.有一个正方体,每个面上分别标有数字1、2、3、4、5、6,下面是从不同角度观察到这个正方体的情况。
1对面是( ) 2对面是( ) 3对面是( )
15.一个立体图形,从正面和上面看到的形状都是,搭这样的立体图形最少需要( )块相同的小正方体。
16.下面物体都是由5个正方体摆成的.从正面看到的图形是的有( );从左面看到的图形是的有( );从上面看到的图形是的有( ).
A. B. C. D. E.
三、判断题
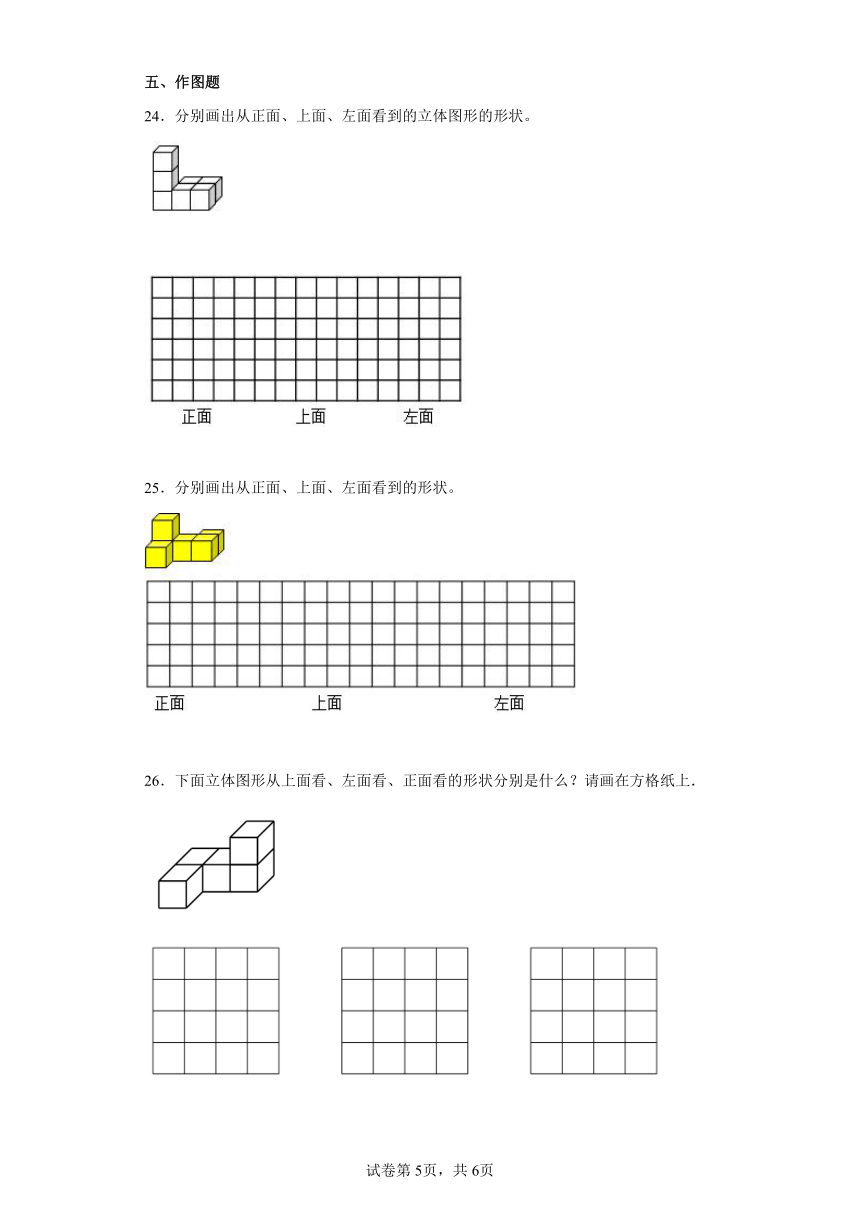
17.从不同的角度观察一个长方体,最多可以看到长方体的3个面。( )
18.由几个相同的小正方体搭成立体图形,从左面看是。( )
19.两个完全一样的正方体排在一起,分别从正面、左面两个方向看,至少有一个方向能看到两个正方体。 ( )
20.由5个小正方体搭成的立体图形,无论从哪个方向看都不可能看到 。 ( )
四、连线题
21.请你连一连,下面的图形分别是谁看到的?
22.
23.
五、作图题
24.分别画出从正面、上面、左面看到的立体图形的形状。
25.分别画出从正面、上面、左面看到的形状。
26.下面立体图形从上面看、左面看、正面看的形状分别是什么?请画在方格纸上.
六、解答题
27.如图,是由方块组成的图形的俯视图和左视图,组成这样的图形最多需要多少方块?最少需要多少方块?
28.按要求摆小正方体:用5个小正方体摆从正面看到的图形(你能摆出几种不同的方法)。
29.添一个小正方体,使从正面看形状不变。有几种添法?
30.一个立体图形,从上面看到的形状是,从正面看到的形状是。搭一个这样的立体图形,最少需要几个小正方体?最多可以有几个小正方体?
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.C
【分析】通过观察可知,该几何体一共有4个小正方体组成,其中前排有3个,后排中间有1个,据此解答。
【详解】观察从正面和上面看到的图形可知,该几何体一共有4个小正方体组成,其中前排有3个,后排中间有1个,则从左面看到的是左右并排的两个小正方形。
故选择:C
【点睛】此题考查了从不同方向观察物体的问题,关键是结合题中两个方向看到的图形确定几何体形状。
2.C
【分析】从上面看是,可知最下面一层是4个小正方体,摆放方式如从上面看到的形状,根据从正面和左面看到的图形可知,第二层有1个小正方体,在第一排中间的小正方体上面。据此解答。
【详解】由分析可知,需要4+1=5个小正方体,能搭出符合题意要求的几何体。
故选答案为:C
【点睛】此题考查了根据三视图确定几何体,锻炼了学生的观察能力和空间想象能力。
3.B
【分析】逐项分析,找出错误的一项即可。
【详解】A. 成语“登高望远”是指站得越高,看的越远,观察到的范围越大。原题说法正确。
B. 晚上散步时如果逐渐向路灯走近,影子就会逐渐变短,原题说法错误。
C. 站在两个不同方向拍同一建筑物,拍出的照片有可能是一样的。原题说法正确。
故答案为:B
【点睛】此题主要考查了观察的范围以及从不同方向观察物体,认真解答即可。
4.A
【分析】根据从正面看到的形状,可以知道从正面看是由3个小正方体组成的;通过上面看到的形状知道3个小正方体中间的那个小正方体里面还有一个小正方体,即从侧面看是两个小正方体,因为多出来的小正方体不是在中间三个小正方体的上面,所以不是D,由此即可判断答案。
【详解】第一排有3个小正方体,从上面看三个小正方体中间的小正方体的上面还有一个,
即右面看到的形状是
故答案为:A。
【点睛】解答此题的关键是根据从正面,上面看到的图形,确定这个立体图形的形状,然后再选择出右面看的形状。
5.C
【分析】观察图形可知,从正面看到的图形是2层,下层3个正方形,上层2个靠左边;据此解答。
【详解】由分析可知:从正面观察看到的形状是。
故答案为:C
【点睛】本题是考查从不同方向观察物体和几何体,进一步考查了学生的空间想象力。
6.B
【分析】观察的范围随着观察点的变化而改变,观察点越高,观察的范围越大,观察点越低,观察的范围越小。
【详解】观察点越高,观察的范围越大,即站得越高,看到的范围越大。
故答案为:B。
【点睛】本题主要考查了观察的范围(视野与盲区),随着观察点的变化,观察的范围也在随着变化。
7.A
【解析】根据从正面看到,从上面看到可知,该物体有前后两排,都只有一层高,以此即可得到从左面看到的图形。
【详解】由主视图和俯视图可知该物体有前后两排,有一层高,则从左面看到。
故答案为:A。
【点睛】本题考查了三视图和展开图,得到该物体的排数和每排的层高是解题的关键。
8.A
【分析】自己动手摆一摆,不同的位置观察到的物体形状可能是相同的,也可能是不同的。观察物体时要从不同角度全面地观察。
【详解】A.从左面看,是4个正方形,下行2个,上行2个;
B.从左面看,是三个正方形,上行1个,下行2个,左面对齐;
C.从左面看,是三个正方形,上行1个,下行2个,左面对齐;
D.从左面看,是三个正方形,上行1个,下行2个,右面对齐。
从左面看到形状是的图形是A;
故答案为:A
【点睛】本题是考查从不同方向观察物体和几何图形。是培养学生的观察能力。
9.A
【分析】观察物体时,观察点越低,观察的范围越小;观察点越高,观察的范围越大,据此解答。
【详解】图中,A、B、C三点,A点最高,所以安装在A点监控到地面的范围最大。
【点睛】此题考查了观察的范围,属于基础类题目,认真解答即可。
10. 5 7
【分析】可以先从上面看的形状,只需要4块,然后设法满足从右面看的形状,得到所需最少的个数,在保证从上面看、从右面看的形状不变的情况下增加,得到最多的个数。
【详解】如图所示,左图是满足要求的最少个数,需要5个小正方体,右图是满足要求的最多个数,需要7个小正方体;
【点睛】一般情况下,给出三视图中的三个,可以确定几何体,只给出两个,只能确定出一个范围。
11. 正 侧
【分析】观察立体图形,从正面看到的是,从上面看到的是,从侧面看到的是,据此解答。
【详解】通过观察,从正面看到的形状是,从侧面看到的形状是。
【点睛】本题考察立体图形三视图的认识,运用空间想象力是解题的关键。
12. ③ ①②④ ①②④ ③ ①
【分析】从不同的方向观察物体时,因观察的方向不同,观察到物体的形状也不相同,据此观察出每个立体图形不同方向的图形,进行解答即可。
【详解】从正面看是的有:;
从正面看是的有:、、;
从侧面看是的有:、、;
从上面看是的有:;
从上面看是的有:。
【点睛】此题考查了从不同方向观察物体和几何体,锻炼了学生的空间想象力和抽象思维能力。
13.5
【解析】略
14. 5 6 4
【详解】略
15.4
【详解】略
16. ABE AC ABC
【详解】略
17.√
【分析】根据题意可知站在不同位置观察同一个长方体,可能会看到1个面,也可能看到2个面,最多看到3个面。
【详解】站在不同位置观察同一个长方体,最多能看到长方体的3个面。
所以判断正确。
【点睛】本题主要考查从不同角度观察一个物体能看到这个物体的多少,记住从不同位置观察长方体最多看到3个面,正方体也是最多看到3个面。
18.×
【分析】从左面观察立体图形,看到2层,上层1个小正方形靠右、下层2个小正方形;据此解答。
【详解】由几个相同的小正方体搭成立体图形,从左面看是,所以原题说法错误。
故答案为:×。
【点睛】本题主要考查物体三视图的认识,解题时注意区分左、右面。
19.√
【分析】无论这两个正方体横向、纵向、前后放,组合成长方体,从正面、左面两个方向看,至少有一个方向能看到两个正方体。
【详解】由分析可知,如图:
(左图、右图从正面能看到两个正方体,中图从左面能看到两个正方体)
两个完全一样的正方体排在一起,分别从正面、左面两个方向看,至少有一个方向能看到两个正方体,原题的说法正确。
故答案为:√
【点睛】此题主要是考查从不同的方向观察物体和几何体,这两个正方体组成的长方体,不管怎么放置,从正面、左面总能看到两个正方体。
20.×
【分析】此题可以举例说明:如果把5个小正方体排成一行两层:下层3个正方体,上层2个正方体,此时从上面看到的图形就是一行3个正方形,据此即可判断。
【详解】如图: ,这个图形就是5个小正方体组成的图形,它从上面看到的图形就是 ;
故答案为:×
【点睛】本题考查了从不同方向观察几何体,观察时要注意每个面有几排(层),每排(层)有几个,每排(层)的形状是什么样。
21.见详解
【分析】小鸟在房子的上面,它看到的是房子上面黑色的瓦片,小兔子在房子的前面,它看到的是房子的大门,蜗牛在房子的右侧面,它看到的是房子的窗户。
【详解】
【点睛】本题是考查从不同方向观察物体和几何体,能正确辨认从正面、上面、左面(或右面)观察到的物体和简单几何体的平面图形。
22.见详解
【分析】观察图形可知,从正面看是两层,下层有三个正方形,上面有一个正方形且和左面对齐;从上面看是两行,前行三个正方形,下行三个正方形,且左右对齐;从左面看两层,下层有两个正方形,上层有一个正方形,且和左边对齐,据此连线。
【详解】
【点睛】本题考查从不同方向观察物体和几何体,锻炼空间想象力和抽象思维能力。
23.见详解
【分析】观察图形可知,从正面看和从上面看的图形都是一行4个正方形,从右面看到一个正方形,据此画线。
【详解】
【点睛】本题考查从不同方向观察物体和几何体,锻炼空间想象力和抽象思维能力。
24.见详解
【分析】观察几何体可知,从正面看,有3层,下层3个小正方形,中层和上层都是1个小正方形,左对齐;从上面看有2层,下层3个小正方形,上层2个小正方形,右对齐;从左面看有3层,下层2个小正方形,中层和上层都是1个小正方形,右对齐,据此画图即可。
【详解】画图如下:
【点睛】此题考查了画几何体的三视图,看准每个小正方形的相对位置画图即可。同时培养了学生的观察能力和空间想象能力。
25.见详解
【分析】从上面看到2层,上层1个正方形(在最左侧),下层3个正方形;从上面看到3行,中间3个正方形,上行1个正方形,与中行最右侧正方形相对;下行1个正方形,与中行最左侧正方形相对;从左面看到2层,上层1个正方形(在中间),下层3个正方形;据此解答。
【详解】根据分析画图如下:
【点睛】本题主要考查几何体三视图的画法。
26.
【详解】略
27.6块 8块
【详解】如图
组成这样的图形最少需要6个方块,最多需要8个方块(下图):
【点睛】根据从上面、左面看到的形状,所用的小正方体分前、后两排,上、下两层.下层前、后排各两个,前排左边一个与后排右面一个对齐;上层前、后排最少各放1个,最多各放2个.
28.(1)可以在左边的正方体后面连续摆3个。(答案不唯一)
(2)在左边最下边正方体后面连续摆2个。(答案不唯一)
(3)在正面图形的后面任意位置都可以摆放1个正方体。(答案不唯一)
【详解】略
29.6种
【分析】从正面看,形状不变,有6种摆法,只要摆在每个正方体的前面或后面即可;据此解答。
【详解】给添一个小正方体,若从正面看形状不变,只要摆在每个正方体的前面或后面即可,共有6种不同的摆法。
答:有6种添法。
【点睛】此题考查了从不同方向观察物体和几何体,锻炼了学生的空间想象力和抽象思维能力。
30.最少需要5个,最多可以有6个。
【详解】略
答案第1页,共2页
答案第1页,共2页
北师大版数学六年级上册单元测试卷
第三单元 观察物体
学校:___________姓名:___________班级:___________考号:___________
题号 一 二 三 四 五 六 总分
得分
一、选择题
1.用同样大小的正方体摆成物体(两个正方体之间至少有一个面重叠),从正面看到的是,从上面看到的是,从左面看到的是( )。
A. B. C. D.无法确定
2.如图,搭出同时符合下面要求的几何体,需要( )个小正方体。
A.3 B.4 C.5 D.6
3.下列关于观察物体的说法,错误的是( )。
A.成语“登高望远”是指站得越高,观察到的范围越大。
B.晚上散步时如果逐渐向路灯走近,影子就会逐渐变长。
C.站在两个不同方向拍同一建筑物,拍出的照片有可能是一样的。
4.用大小相同的小正方体搭成一个立体图形,从正面看到的形状是,从上面看到的形状是,从右面看到的形状是( )。
A. B. C. D.
5.从正面观察下面的立体图形,看到的形状是( )。
A. B. C.
6.“欲穷千里目,更上一层楼”用数学的知识解释是站得越高,看到的范围( )。
A.越小 B.越大 C.不变 D.没有变化
7.用4个同样大小的正方体摆成的形状,从正面看是,从上面看是,从左面看是( )。
A. B. C.
8.在下面的4个几何体中,从左面看到形状是的图形是( )。
A. B.
C. D.
二、填空题
9.如图,某学校在教学楼安装摄像头,安装在( )点监控到地面的范围最大。
10.一个立体图形,从右面看到的形状是,从上面看到的形状是,搭这样的一个立体图形,最少需要( )个小方体,最多可以用( )个小立方体。
11.如图,从( )面看到的形状是,从( )面看到的形状是。
12.分一分,填一填。(填序号)
从正面看是图A的有( );从正面看是图B的有( );从侧面看是图B的有( );从上面看是图C的有( );从上面看是图D的有( )。
13.一个立体图形,从前面与上面看到的形状都是 ,从左面看到的形状是,想一想,搭这样的立体图形,至少要用( )个小立方体。
14.有一个正方体,每个面上分别标有数字1、2、3、4、5、6,下面是从不同角度观察到这个正方体的情况。
1对面是( ) 2对面是( ) 3对面是( )
15.一个立体图形,从正面和上面看到的形状都是,搭这样的立体图形最少需要( )块相同的小正方体。
16.下面物体都是由5个正方体摆成的.从正面看到的图形是的有( );从左面看到的图形是的有( );从上面看到的图形是的有( ).
A. B. C. D. E.
三、判断题
17.从不同的角度观察一个长方体,最多可以看到长方体的3个面。( )
18.由几个相同的小正方体搭成立体图形,从左面看是。( )
19.两个完全一样的正方体排在一起,分别从正面、左面两个方向看,至少有一个方向能看到两个正方体。 ( )
20.由5个小正方体搭成的立体图形,无论从哪个方向看都不可能看到 。 ( )
四、连线题
21.请你连一连,下面的图形分别是谁看到的?
22.
23.
五、作图题
24.分别画出从正面、上面、左面看到的立体图形的形状。
25.分别画出从正面、上面、左面看到的形状。
26.下面立体图形从上面看、左面看、正面看的形状分别是什么?请画在方格纸上.
六、解答题
27.如图,是由方块组成的图形的俯视图和左视图,组成这样的图形最多需要多少方块?最少需要多少方块?
28.按要求摆小正方体:用5个小正方体摆从正面看到的图形(你能摆出几种不同的方法)。
29.添一个小正方体,使从正面看形状不变。有几种添法?
30.一个立体图形,从上面看到的形状是,从正面看到的形状是。搭一个这样的立体图形,最少需要几个小正方体?最多可以有几个小正方体?
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.C
【分析】通过观察可知,该几何体一共有4个小正方体组成,其中前排有3个,后排中间有1个,据此解答。
【详解】观察从正面和上面看到的图形可知,该几何体一共有4个小正方体组成,其中前排有3个,后排中间有1个,则从左面看到的是左右并排的两个小正方形。
故选择:C
【点睛】此题考查了从不同方向观察物体的问题,关键是结合题中两个方向看到的图形确定几何体形状。
2.C
【分析】从上面看是,可知最下面一层是4个小正方体,摆放方式如从上面看到的形状,根据从正面和左面看到的图形可知,第二层有1个小正方体,在第一排中间的小正方体上面。据此解答。
【详解】由分析可知,需要4+1=5个小正方体,能搭出符合题意要求的几何体。
故选答案为:C
【点睛】此题考查了根据三视图确定几何体,锻炼了学生的观察能力和空间想象能力。
3.B
【分析】逐项分析,找出错误的一项即可。
【详解】A. 成语“登高望远”是指站得越高,看的越远,观察到的范围越大。原题说法正确。
B. 晚上散步时如果逐渐向路灯走近,影子就会逐渐变短,原题说法错误。
C. 站在两个不同方向拍同一建筑物,拍出的照片有可能是一样的。原题说法正确。
故答案为:B
【点睛】此题主要考查了观察的范围以及从不同方向观察物体,认真解答即可。
4.A
【分析】根据从正面看到的形状,可以知道从正面看是由3个小正方体组成的;通过上面看到的形状知道3个小正方体中间的那个小正方体里面还有一个小正方体,即从侧面看是两个小正方体,因为多出来的小正方体不是在中间三个小正方体的上面,所以不是D,由此即可判断答案。
【详解】第一排有3个小正方体,从上面看三个小正方体中间的小正方体的上面还有一个,
即右面看到的形状是
故答案为:A。
【点睛】解答此题的关键是根据从正面,上面看到的图形,确定这个立体图形的形状,然后再选择出右面看的形状。
5.C
【分析】观察图形可知,从正面看到的图形是2层,下层3个正方形,上层2个靠左边;据此解答。
【详解】由分析可知:从正面观察看到的形状是。
故答案为:C
【点睛】本题是考查从不同方向观察物体和几何体,进一步考查了学生的空间想象力。
6.B
【分析】观察的范围随着观察点的变化而改变,观察点越高,观察的范围越大,观察点越低,观察的范围越小。
【详解】观察点越高,观察的范围越大,即站得越高,看到的范围越大。
故答案为:B。
【点睛】本题主要考查了观察的范围(视野与盲区),随着观察点的变化,观察的范围也在随着变化。
7.A
【解析】根据从正面看到,从上面看到可知,该物体有前后两排,都只有一层高,以此即可得到从左面看到的图形。
【详解】由主视图和俯视图可知该物体有前后两排,有一层高,则从左面看到。
故答案为:A。
【点睛】本题考查了三视图和展开图,得到该物体的排数和每排的层高是解题的关键。
8.A
【分析】自己动手摆一摆,不同的位置观察到的物体形状可能是相同的,也可能是不同的。观察物体时要从不同角度全面地观察。
【详解】A.从左面看,是4个正方形,下行2个,上行2个;
B.从左面看,是三个正方形,上行1个,下行2个,左面对齐;
C.从左面看,是三个正方形,上行1个,下行2个,左面对齐;
D.从左面看,是三个正方形,上行1个,下行2个,右面对齐。
从左面看到形状是的图形是A;
故答案为:A
【点睛】本题是考查从不同方向观察物体和几何图形。是培养学生的观察能力。
9.A
【分析】观察物体时,观察点越低,观察的范围越小;观察点越高,观察的范围越大,据此解答。
【详解】图中,A、B、C三点,A点最高,所以安装在A点监控到地面的范围最大。
【点睛】此题考查了观察的范围,属于基础类题目,认真解答即可。
10. 5 7
【分析】可以先从上面看的形状,只需要4块,然后设法满足从右面看的形状,得到所需最少的个数,在保证从上面看、从右面看的形状不变的情况下增加,得到最多的个数。
【详解】如图所示,左图是满足要求的最少个数,需要5个小正方体,右图是满足要求的最多个数,需要7个小正方体;
【点睛】一般情况下,给出三视图中的三个,可以确定几何体,只给出两个,只能确定出一个范围。
11. 正 侧
【分析】观察立体图形,从正面看到的是,从上面看到的是,从侧面看到的是,据此解答。
【详解】通过观察,从正面看到的形状是,从侧面看到的形状是。
【点睛】本题考察立体图形三视图的认识,运用空间想象力是解题的关键。
12. ③ ①②④ ①②④ ③ ①
【分析】从不同的方向观察物体时,因观察的方向不同,观察到物体的形状也不相同,据此观察出每个立体图形不同方向的图形,进行解答即可。
【详解】从正面看是的有:;
从正面看是的有:、、;
从侧面看是的有:、、;
从上面看是的有:;
从上面看是的有:。
【点睛】此题考查了从不同方向观察物体和几何体,锻炼了学生的空间想象力和抽象思维能力。
13.5
【解析】略
14. 5 6 4
【详解】略
15.4
【详解】略
16. ABE AC ABC
【详解】略
17.√
【分析】根据题意可知站在不同位置观察同一个长方体,可能会看到1个面,也可能看到2个面,最多看到3个面。
【详解】站在不同位置观察同一个长方体,最多能看到长方体的3个面。
所以判断正确。
【点睛】本题主要考查从不同角度观察一个物体能看到这个物体的多少,记住从不同位置观察长方体最多看到3个面,正方体也是最多看到3个面。
18.×
【分析】从左面观察立体图形,看到2层,上层1个小正方形靠右、下层2个小正方形;据此解答。
【详解】由几个相同的小正方体搭成立体图形,从左面看是,所以原题说法错误。
故答案为:×。
【点睛】本题主要考查物体三视图的认识,解题时注意区分左、右面。
19.√
【分析】无论这两个正方体横向、纵向、前后放,组合成长方体,从正面、左面两个方向看,至少有一个方向能看到两个正方体。
【详解】由分析可知,如图:
(左图、右图从正面能看到两个正方体,中图从左面能看到两个正方体)
两个完全一样的正方体排在一起,分别从正面、左面两个方向看,至少有一个方向能看到两个正方体,原题的说法正确。
故答案为:√
【点睛】此题主要是考查从不同的方向观察物体和几何体,这两个正方体组成的长方体,不管怎么放置,从正面、左面总能看到两个正方体。
20.×
【分析】此题可以举例说明:如果把5个小正方体排成一行两层:下层3个正方体,上层2个正方体,此时从上面看到的图形就是一行3个正方形,据此即可判断。
【详解】如图: ,这个图形就是5个小正方体组成的图形,它从上面看到的图形就是 ;
故答案为:×
【点睛】本题考查了从不同方向观察几何体,观察时要注意每个面有几排(层),每排(层)有几个,每排(层)的形状是什么样。
21.见详解
【分析】小鸟在房子的上面,它看到的是房子上面黑色的瓦片,小兔子在房子的前面,它看到的是房子的大门,蜗牛在房子的右侧面,它看到的是房子的窗户。
【详解】
【点睛】本题是考查从不同方向观察物体和几何体,能正确辨认从正面、上面、左面(或右面)观察到的物体和简单几何体的平面图形。
22.见详解
【分析】观察图形可知,从正面看是两层,下层有三个正方形,上面有一个正方形且和左面对齐;从上面看是两行,前行三个正方形,下行三个正方形,且左右对齐;从左面看两层,下层有两个正方形,上层有一个正方形,且和左边对齐,据此连线。
【详解】
【点睛】本题考查从不同方向观察物体和几何体,锻炼空间想象力和抽象思维能力。
23.见详解
【分析】观察图形可知,从正面看和从上面看的图形都是一行4个正方形,从右面看到一个正方形,据此画线。
【详解】
【点睛】本题考查从不同方向观察物体和几何体,锻炼空间想象力和抽象思维能力。
24.见详解
【分析】观察几何体可知,从正面看,有3层,下层3个小正方形,中层和上层都是1个小正方形,左对齐;从上面看有2层,下层3个小正方形,上层2个小正方形,右对齐;从左面看有3层,下层2个小正方形,中层和上层都是1个小正方形,右对齐,据此画图即可。
【详解】画图如下:
【点睛】此题考查了画几何体的三视图,看准每个小正方形的相对位置画图即可。同时培养了学生的观察能力和空间想象能力。
25.见详解
【分析】从上面看到2层,上层1个正方形(在最左侧),下层3个正方形;从上面看到3行,中间3个正方形,上行1个正方形,与中行最右侧正方形相对;下行1个正方形,与中行最左侧正方形相对;从左面看到2层,上层1个正方形(在中间),下层3个正方形;据此解答。
【详解】根据分析画图如下:
【点睛】本题主要考查几何体三视图的画法。
26.
【详解】略
27.6块 8块
【详解】如图
组成这样的图形最少需要6个方块,最多需要8个方块(下图):
【点睛】根据从上面、左面看到的形状,所用的小正方体分前、后两排,上、下两层.下层前、后排各两个,前排左边一个与后排右面一个对齐;上层前、后排最少各放1个,最多各放2个.
28.(1)可以在左边的正方体后面连续摆3个。(答案不唯一)
(2)在左边最下边正方体后面连续摆2个。(答案不唯一)
(3)在正面图形的后面任意位置都可以摆放1个正方体。(答案不唯一)
【详解】略
29.6种
【分析】从正面看,形状不变,有6种摆法,只要摆在每个正方体的前面或后面即可;据此解答。
【详解】给添一个小正方体,若从正面看形状不变,只要摆在每个正方体的前面或后面即可,共有6种不同的摆法。
答:有6种添法。
【点睛】此题考查了从不同方向观察物体和几何体,锻炼了学生的空间想象力和抽象思维能力。
30.最少需要5个,最多可以有6个。
【详解】略
答案第1页,共2页
答案第1页,共2页
同课章节目录
- 一 圆
- 1 圆的认识(一)
- 2 圆的认识(二)
- 3 欣赏与设计
- 4 圆的周长
- 5 圆的面积(一)
- 6 圆的面积(二)
- 二 分数的混合运算
- 1 分数的混合运算(一)
- 2 分数的混合运算(二)
- 3 分数的混合运算(三)
- 三 观察物体
- 1 搭积木比赛
- 2 观察的范围
- 3 天安门广场
- 四 百分数
- 1 百分数的认识
- 2 合格率
- 3 营养含量
- 4 这月我当家
- 五 数据处理
- 1 扇形统计图
- 2 统计图的选择
- 3 身高的情况
- 4 身高的变化
- 六 比的认识
- 1 生活中的比
- 2 比的化简
- 3 比的应用
- 数学好玩
- 1 反弹高度
- 2 看图找关系
- 3 比赛场次
- 七 百分数的应用
- 1 百分数的应用(一)
- 2 百分数的应用(二)
- 3 百分数的应用(三)
- 4 百分数的应用(四)
