北师大版数学五年级上册单元测试卷-第七单元 可能性 (含答案)
文档属性
| 名称 | 北师大版数学五年级上册单元测试卷-第七单元 可能性 (含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 487.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-17 10:51:34 | ||
图片预览



文档简介
保密★启用前
北师大版数学五年级上册单元测试卷
第七单元 可能性
学校:___________姓名:___________班级:___________考号:___________
题号 一 二 三 四 五 六 总分
得分
一、选择题
1.投掷5次硬币,有3次正面朝上,2次反面朝上,那么投掷第6次硬币正面朝上的可能性是( )。
A. B. C. D.
2.转动指针,停在阴影处可能性最大的是( )。
A. B. C.
3.指针转动后,( )停在绿色上。
A.可能 B.一定 C.不可能
4.下边是某商场用来抽奖的转盘。转动指针,指针停在红色区域,得一等奖,停在其他区域得纪念奖。在这个商场购物的顾客能得到一等奖。( )
A.经常 B.偶尔 C.不可能
5.从只装有10个红球的盒子里( )摸出黄球。
A.一定 B.可能 C.不可能
6.淘气抛硬币,连续抛8次都是正面,抛第9次( )是正面。
A.一定 B.不可能 C.可能
7.在一个正方体的六个面分别标上1~6六个数,小明和小亮用它来做游戏。两人各任意抛30次,朝上面的数比4大算小明赢,否则算小亮赢,这种游戏的结果,( )。
A.小明赢的可能性大
B.小亮赢的可能性大
C.两人赢的可能性一样
8.转动转盘,指针会偶尔指向哪个区域?( )
A.红色 B.蓝色 C.黄色
二、填空题
9.盒子里有两种不同颜色的球,笑笑摸了50次,摸球的情况如下表。
颜色 红色 黄色
次数 12 38
根据表中的数据推测,盒子里( )色的球可能多,( )色的球可能少。
10.口袋里大小相同的8个红球和4个黄球,从中任意摸出1个球,摸到( ) 球的可能性大,摸到( ) 球的可能性小。
11.口袋里有形状大小相同的8只红袜子和4只黄袜子,从中任意摸出1只袜子,摸出红袜子的可能性是____,摸出黄袜子的可能性是____。
12.一个茶杯杯口向上放在桌子上,翻动1次杯口朝下,翻动2次杯口朝上,翻动2008次杯口向________,翻动87次杯口向________.
13.如下图,商场开展“即摸即中”有奖促销活动,箱子里放入分别写有1~10的10个小球.顾客得到( )的可能性最大,得到( )的可能性最小。
14.转动转盘,指针停在________色区域的可能性最大;停在________色区域的可能性最小。
15.把3个白球和5个红球放在盒子里,任意摸出一个,________是蓝色的。(选填“可能”、“一定”或“不可能”)
16.欢欢和乐乐想做摸球游戏,每次任意摸1个球,然后放回再摇匀,每人摸20次.
摸到红球欢欢得1分,摸到黄球乐乐得1分,摸到其他颜色的球两人都不得分.你认为从哪几个口袋里摸球是公平的?
你的选择是:________。
三、判断题
17.盒子里有99个红球,1个白球,任意摸出一个球,不可能是白球。( )
18.小明共摸出16次红球,4次白球,盒子里红球可能多一些。( )
19.小明和小华下棋比赛,用投掷一颗骰子的方法决定谁先走。如果大于4小明先走,为了保证公平,小于3应该小华先走。( )
20.如下图所示,转动转盘,指针指向偶数的可能性大。( )
四、连线题
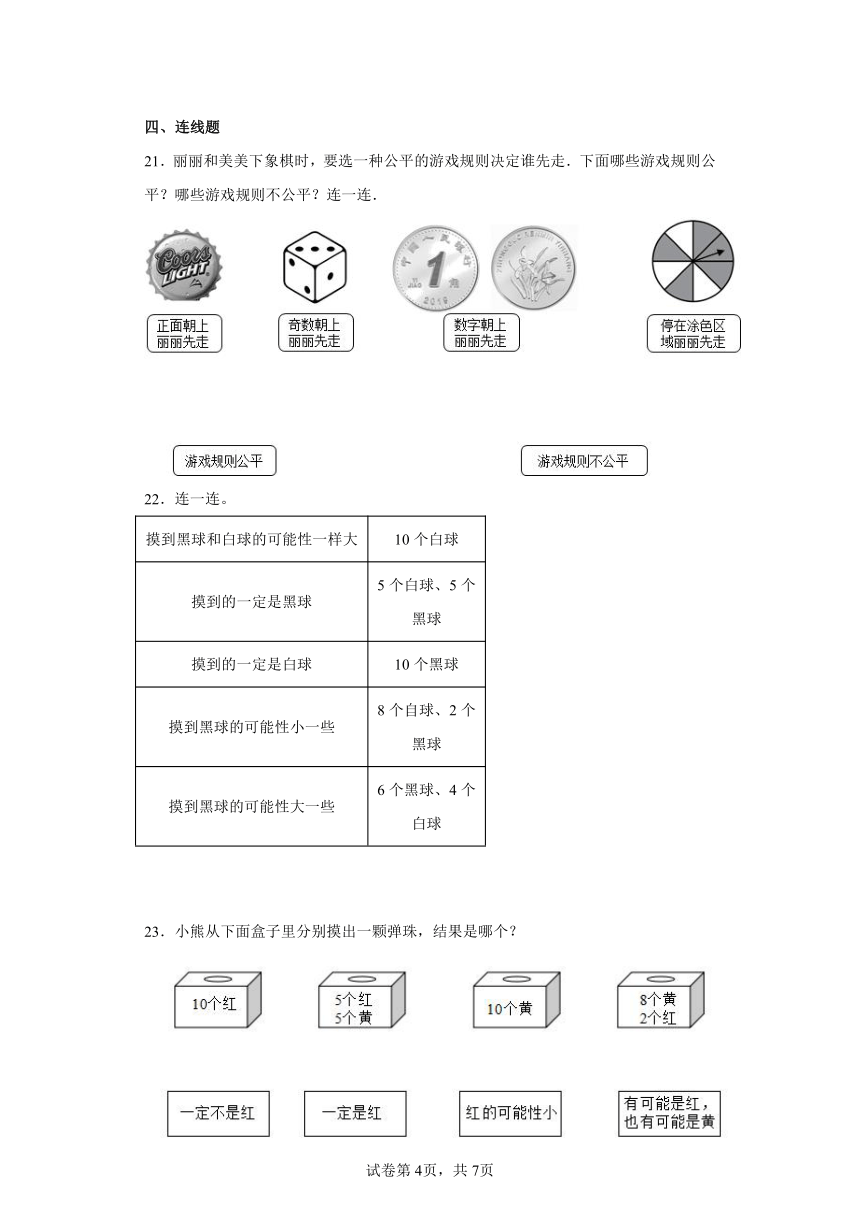
21.丽丽和美美下象棋时,要选一种公平的游戏规则决定谁先走.下面哪些游戏规则公平?哪些游戏规则不公平?连一连.
22.连一连。
摸到黑球和白球的可能性一样大 10个白球
摸到的一定是黑球 5个白球、5个黑球
摸到的一定是白球 10个黑球
摸到黑球的可能性小一些 8个自球、2个黑球
摸到黑球的可能性大一些 6个黑球、4个白球
23.小熊从下面盒子里分别摸出一颗弹珠,结果是哪个?
五、作图题
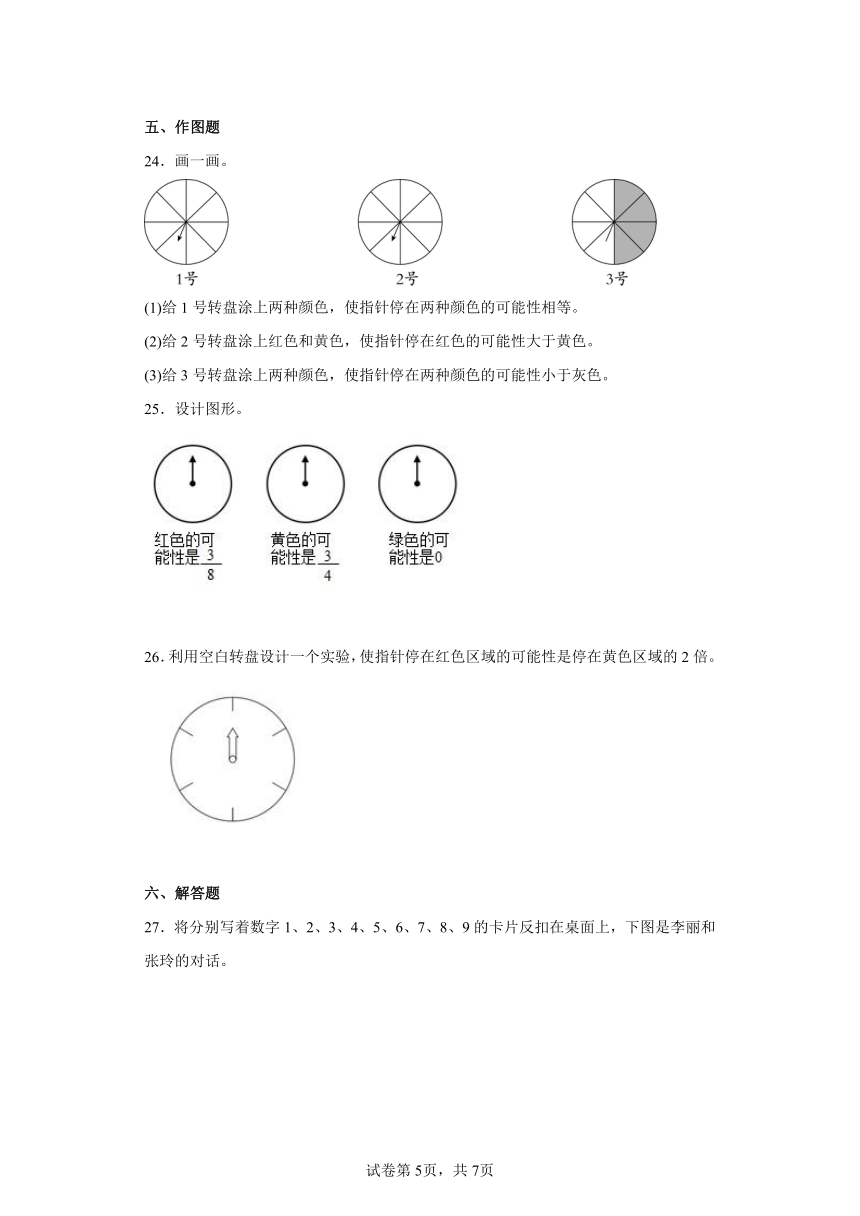
24.画一画。
(1)给1号转盘涂上两种颜色,使指针停在两种颜色的可能性相等。
(2)给2号转盘涂上红色和黄色,使指针停在红色的可能性大于黄色。
(3)给3号转盘涂上两种颜色,使指针停在两种颜色的可能性小于灰色。
25.设计图形。
26.利用空白转盘设计一个实验,使指针停在红色区域的可能性是停在黄色区域的2倍。
六、解答题
27.将分别写着数字1、2、3、4、5、6、7、8、9的卡片反扣在桌面上,下图是李丽和张玲的对话。
(1)这个游戏规则公平吗?为什么?
(2)请设计一个对双方都公平的游戏规则。
28.有一些装有球的盒子,3个小朋友每人摸了30次,并作了记录.请你猜一猜,他们分别摸的是哪个盒子里的球?用线连一连.
29.盒子中装有三种颜色的球一共7个,同学们轮流从盒子中摸出1个球,作记录后再放回盒内。摸出球的颜色与次数统计如下:
颜色 白色 黄色 红色 蓝色
次数 48 12 24 0
盒子中装了哪几种颜色的球?
30.芳芳和丽丽做摸球游戏,每次从盒子里任意摸一个球,放回后摇匀,每人摸20次,记录如下。
芳芳 丽丽
颜色 白球 黑球 黄球 白球 黑球
次数 12 7 1 14 6
盒子里哪种颜色的球可能最多?哪种颜色的球可能最少?
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.D
【分析】可能性大小就是事情出现的概率,可能性=所求情况数÷总情况数;因为硬币只有正反两面,所以每一面出现的可能性都是,据此解答。
【详解】1÷2=
故答案为:D
【点睛】本题考查了简单事件发生的可能性的求解,注意:不要被一些无用的信息所迷惑。
2.A
【分析】首先观察转盘图可得:把这个大转盘平均分成8份,数一数哪一个图形阴影部分的份数多哪一个的可能性就大。
【详解】A.把这个大转盘平均分成8份,阴影部分是5份;
B.把这个大转盘平均分成8份,阴影部分是3份;
C.把这个大转盘平均分成8份,阴影部分是1份;
所以5>3>1,停在阴影处可能性最大的是A。
故答案为:A
【点睛】此题主要考查可能性的大小的判断。针对此题,圆的面积相等,平均分的份数相等,所以只需要看阴影的份数即可解答。
3.C
【分析】因为整个圆的面积上没有绿色的面积,所以指针不可能停在绿色面积区域。
【详解】由分析知:因为整个圆的面积上没有绿色的面积,所以指针不可能停在绿色面积区域。
故答案为:C
【点睛】解答此题根据可能性的大小进行分析,因为没有绿色的面积,所以指针不可能停在绿色面积区域。
4.B
【分析】可能性的大小与数据的多少有关系,数据越多,摸出的可能性越大,据此解答。
【详解】观察转盘可知,转盘被平均分成8份,红色有两份,白色有6份,所以停在红色区域的可能性小于其他区域,得一等奖的机会不多,偶尔可能得到。
故答案为:B。
【点睛】本题主要考查了学生对可能性大小知识的掌握情况。
5.C
【分析】必然事件指在一定条件下,一定发生的事件;
不可能事件是指在一定条件下,一定不发生的事件;
不确定事件即随机事件是指在一定条件下,可能发生也可能不发生的事件。
【详解】在一个只装有10个红球的盒子里,摸出黄球是不可能的,
因而这是一个不可能事件。
故答案为:C
【点睛】解决本题要正确理解必然事件、不可能事件、随机事件的概念;一定不发生的事件叫不可能事件。
6.C
【分析】硬币有正、反两面,抛硬币,正、反面的可能性各占一半,都有可能;属于不确定事件,但在一定条件下,可能发生,也可能不发生的事件;进而选择即可。
【详解】由分析知:抛第9次,正、反面都有可能,可能性大小相等。
故答案为:C
【点睛】解答此题应根据可能性的大小进行分析,与所抛次数无关,别被无用数字所迷惑。
7.B
【分析】因两人抛的次数相同,都是30次,“一个正方体的六个面分别标上1~6六个数”,比4大的数有两个数,小于等于4的数有4个,分别求出抛1次出现可能性,再比较即可。
因抛的次数相同,所以只比较抛一次出现的可能性的大小。
【详解】比4大的可能性:2÷6=
小于等于4的可能性:4÷6=
,所以出现大于4的可能性小。
所以小亮赢的可能性大。
故答案为:B
【点睛】本题的关键是分别求出出现大于4的和小于等于4的可能性,再进行比较。
8.C
【分析】要求转动转盘指针会偶尔指向哪个区域,也就是求指针指向哪一个颜色区域的可能性小,由图可知,黄色区域最小,所以指针会偶尔指向黄色区域;据此解答。
【详解】由图可知,黄色区域最小,所以指针会偶尔指向黄色区域。
故答案为:C
【点睛】此题考查了可能性大小的判断,所占区域面积小的可能性就小。
9. 黄 红
【分析】根据摸到不同颜色球的次数进行判断,摸到的次数多,则盒子里这种颜色的球可能多。
【详解】摸了50次,摸到红球12次,黄球38次,38>12,则根据表中的数据推测,盒子里黄色的球可能多,红色的球可能少。
【点睛】本题考查可能性的大小,根据不同颜色的球的次数即可解答。
10. 红 黄
【分析】比较两种球的数量,数量多的可能性就大。
【详解】因为球的总数不变,红球的个数多,黄球的个数少,所以任意摸出一个球,摸到红球的可能性比较大,摸到黄球的可能性较小。
【点睛】此题也可以通过计算摸到红球和黄球的可能性分别是几分之几,进而比较得解。
11.
【分析】先用“8+4”求出口袋中的袜子的总只数,求摸出红袜子和黄袜子的可能性,根据可能性的求法:即求一个数是另一个数的几分之几,用除法分别解答即可。
【详解】8+4=12(只)
8÷12=
4÷12=
答:摸出红袜子的可能性是,摸出黄袜子的可能性是;
故答案为:,。
【点睛】解答此题应根据可能性的求法:即求一个数是另一个数的几分之几用除法解答,进而得出结论。
12. 上 下
【分析】由于当翻动奇数次时,杯口向下,偶数次时,杯口向上,2008为偶数,则翻动2008次时,杯口向上,87为奇数,则当翻动87次时,杯口向下。
【详解】根据分析可知,翻动2008次杯口向上,翻动87次杯口向下。
【点睛】由“一个茶杯杯口向上放在桌子上,翻动1次杯口朝下,翻动2次杯口朝上”,得出“翻动奇数次时,杯口向下,偶数次时,杯口向上”,是解答此题的关键。
13. 口香糖 手套
【分析】任意摸出的一个球,数量多的被摸到的可能性要大,数量少的可能性就小,由此可知:在1到10这10个数字中,小于10的偶数有2、4、6、8,共4个数字;是5的倍数的数有5、10,共2个数字;既是奇数又是合数的数有9,共1个;据此可知,顾客得到口香糖的可能性最大,得到手套的可能性最小。
【详解】4>2>1
所以,顾客得到口香糖的可能性最大,得到手套的可能性最小。
【点睛】本题考查了可能性问题,每种球都有被模到的可有性,数量多的,摸到的可能性较大,反之,就少。
14. 红 蓝色或绿
【分析】哪个区域的面积大,停在哪个区域的可能性就大,哪个区域的面积小,停在哪个区域的可能性就小;把转盘平均分成4份,红色是2份,指针停在红色区域的可能性最大;蓝色和绿色都是1份,停在蓝色或绿色区域的可能性最小。
【详解】根据分析可知,转动转盘,指针停在红色区域的可能性最大;停在蓝色或绿色区域的可能性最小。
【点睛】本题考查了可能性问题,两种球都有被模到的可有性,数量多的,摸到的可能性较大,反之,就少。
15.不可能
【分析】因为盒子里有3个白球和5个红球,没有蓝球,任意摸出一个,不可能是蓝球,属于确定事件中的不可能事件,据此解答。
【详解】把3个白球和5个红球放在盒子里,任意摸出一个,不可能是蓝色的。
【点睛】考查了对事情发生的确定性与不确定性进行分析。
16.①④
【详解】略
17.×
【分析】因为盒子里共有99个红球,1个白球,则共有100个球;任意摸一个球,白球摸到的概率为总球数的,白球摸到的概率很小,但也有可能;进而得出问题答案。
【详解】由分析可知,一个盒里装有99个红球,1个白球,从盒子里任意摸出一个球,不可能摸出白球,说法错误。
故答案为:×
【点睛】此题应根据题中给出的数据进行分析,先算出这白球所占的概率是多少,进而得出正确的判断。
18.√
【分析】比较摸出哪种球的次数多,那么这种球就可能多一些。
【详解】16比4多得多,那么盒子里红球可能多一些,原题说法正确。
故答案为:√
19.√
【详解】略
20.×
【详解】略
21.
【详解】略
22.见详解
【分析】根据题意,根据可能性的大小进行分析;摸到黑球和白球的可能性一样大,那么黑球和白球的数量要相等;摸到的一定是黑球,说明袋子中都是黑球;摸到的一定是白球,说明袋子中的都是白球;摸到黑球的可能性小写,说明袋子的黑球的数量比白球的数量少;摸到黑球的可能性大一些,说明袋子中的黑球数量比白球多些,据此解答。
【详解】(1)10个白球摸到是白球的可能性为1;
(2)5个白球、5个黑球摸到黑球和白球的可能性均为;
(3)10个黑球摸到是黑球的可能性为1;
(4)8个白球、2个黑球摸到是白球的可能性为,摸到是黑球的可能性为;
(5).6个黑球、4个白球摸到是白球的可能性为,摸到是黑球的可能性为。
【点睛】本题考查可能性的大小,根据求一个数是另一个数的几分之几,进行解答。
23.见详解
【分析】(1)从10个红球里面,只能摸出红球,所以应连“一定是红球”;
(2)有5个黄球、5个红球,因为黄球和红球的个数同样多,所以应连“有可能是红,也有可能是黄”;
(3)从10个黄球里面,只能摸出黄球,所以应连“一定不是红”;
(4)从8个黄球和2个红球里面,可能摸出红球也可能摸出黄球,但由于黄球数量多,所以应连“红的可能性小”。
【详解】见下图:
【点睛】本题考查了确定事件和不确定事件,用到的知识点为:必然事件是指在一定条件下,一定发生的事件;不可能事件是指在一定条件下,一定不发生的事件;
不确定事件即随机事件是指在一定条件下,可能发生也可能不发生的事件。
24.
【详解】略
25.
【解析】略
26.见详解
【分析】把此转盘平均分成6份,使指针停在红色区域的可能性是停在黄色区域的2倍,只要使黄色区域的面积占其中的2份,红色区域的面积占其中的4份即可。
【详解】见下图:
【点睛】解决此题只要使黄色区域的面积占其中的2份,红色区域的面积占其中的4份即可。
27.(1)不公平;理由见详解;
(2)摸到比5大的数李丽赢;摸到比5小的数张玲赢。
【分析】(1)根据奇数、偶数的定义,分别找出1、2、3、4、5、6、7、8、9中奇数与偶数的个数,比较即可判断;(2)使游戏双方获胜的可能性相同即可。
【详解】(1)奇数有:1、3、5、7、9,共5个;
偶数有:2、4、6、8,共4个;
所以摸到奇数、偶数的可能性不同,这个游戏不公平。
(2)比5大的数有4个,比5小的数也有4个,可设定规则为:摸到比5大的数李丽赢;摸到比5小的数张玲赢(答案合理即可)。
【点睛】确定一个游戏是否公平,要先找出事件发生的所有可能,然后看对于游戏双方,获胜的可能性是否相同。若相同,则游戏规则公平;若不相同,则游戏规则不公平。
28.如下:
【分析】根据记录表可知,第一个小朋友摸出红球的可能性大;第二个小朋友摸出白球的可能性大,第三个小朋友摸出红球与白球的可能性差不多;根据求可能性的方法,分别求出这三个盒子中摸出红球与白球的可能性大小,再与已知的记录表比较即可解答.
【详解】每个盒子都是10个球,
第一个盒子有9个白球,所以摸出白球的可能性大,摸出红球的可能性小;
第二个盒子有5个白球5个红球,摸出红球与白球的可能性一样大;
第三个盒子有9个红球,所以摸出红球可能性大,摸出白球的可能性小,据此连线如下:
29.白,黄,红
【分析】从摸出各种颜色球的次数看,盒子里有白球、黄球、红球,没有蓝色的球。
【详解】答:盒子里装了:白色、黄色、红色三种颜色的球。
【点睛】根据可能性大小的知识,解答此题即可。
30.白球;黄球
【分析】可能性表示所求情况的数量占情况总数的几分之几,即可能性=所求事件可能发生的次数÷所有事件可能发生的次数,故出现次数多的可能就多,反之就少;题中通过两人摸球的数据分析可知,白球出现的次数最多,黄球出现的次数最少,因此可以判断白球的数量最多,黄球的数量最少,黑球介于之间。
【详解】根据分析可知,盒子里白色的球可能最多,黄色的球可能最少。
答:盒子里白球的可能最多,黄球可能最少。
【点睛】本题考查主要考查不确定事件中可能性大小的求解方法的灵活运用。
答案第1页,共2页
答案第1页,共2页
北师大版数学五年级上册单元测试卷
第七单元 可能性
学校:___________姓名:___________班级:___________考号:___________
题号 一 二 三 四 五 六 总分
得分
一、选择题
1.投掷5次硬币,有3次正面朝上,2次反面朝上,那么投掷第6次硬币正面朝上的可能性是( )。
A. B. C. D.
2.转动指针,停在阴影处可能性最大的是( )。
A. B. C.
3.指针转动后,( )停在绿色上。
A.可能 B.一定 C.不可能
4.下边是某商场用来抽奖的转盘。转动指针,指针停在红色区域,得一等奖,停在其他区域得纪念奖。在这个商场购物的顾客能得到一等奖。( )
A.经常 B.偶尔 C.不可能
5.从只装有10个红球的盒子里( )摸出黄球。
A.一定 B.可能 C.不可能
6.淘气抛硬币,连续抛8次都是正面,抛第9次( )是正面。
A.一定 B.不可能 C.可能
7.在一个正方体的六个面分别标上1~6六个数,小明和小亮用它来做游戏。两人各任意抛30次,朝上面的数比4大算小明赢,否则算小亮赢,这种游戏的结果,( )。
A.小明赢的可能性大
B.小亮赢的可能性大
C.两人赢的可能性一样
8.转动转盘,指针会偶尔指向哪个区域?( )
A.红色 B.蓝色 C.黄色
二、填空题
9.盒子里有两种不同颜色的球,笑笑摸了50次,摸球的情况如下表。
颜色 红色 黄色
次数 12 38
根据表中的数据推测,盒子里( )色的球可能多,( )色的球可能少。
10.口袋里大小相同的8个红球和4个黄球,从中任意摸出1个球,摸到( ) 球的可能性大,摸到( ) 球的可能性小。
11.口袋里有形状大小相同的8只红袜子和4只黄袜子,从中任意摸出1只袜子,摸出红袜子的可能性是____,摸出黄袜子的可能性是____。
12.一个茶杯杯口向上放在桌子上,翻动1次杯口朝下,翻动2次杯口朝上,翻动2008次杯口向________,翻动87次杯口向________.
13.如下图,商场开展“即摸即中”有奖促销活动,箱子里放入分别写有1~10的10个小球.顾客得到( )的可能性最大,得到( )的可能性最小。
14.转动转盘,指针停在________色区域的可能性最大;停在________色区域的可能性最小。
15.把3个白球和5个红球放在盒子里,任意摸出一个,________是蓝色的。(选填“可能”、“一定”或“不可能”)
16.欢欢和乐乐想做摸球游戏,每次任意摸1个球,然后放回再摇匀,每人摸20次.
摸到红球欢欢得1分,摸到黄球乐乐得1分,摸到其他颜色的球两人都不得分.你认为从哪几个口袋里摸球是公平的?
你的选择是:________。
三、判断题
17.盒子里有99个红球,1个白球,任意摸出一个球,不可能是白球。( )
18.小明共摸出16次红球,4次白球,盒子里红球可能多一些。( )
19.小明和小华下棋比赛,用投掷一颗骰子的方法决定谁先走。如果大于4小明先走,为了保证公平,小于3应该小华先走。( )
20.如下图所示,转动转盘,指针指向偶数的可能性大。( )
四、连线题
21.丽丽和美美下象棋时,要选一种公平的游戏规则决定谁先走.下面哪些游戏规则公平?哪些游戏规则不公平?连一连.
22.连一连。
摸到黑球和白球的可能性一样大 10个白球
摸到的一定是黑球 5个白球、5个黑球
摸到的一定是白球 10个黑球
摸到黑球的可能性小一些 8个自球、2个黑球
摸到黑球的可能性大一些 6个黑球、4个白球
23.小熊从下面盒子里分别摸出一颗弹珠,结果是哪个?
五、作图题
24.画一画。
(1)给1号转盘涂上两种颜色,使指针停在两种颜色的可能性相等。
(2)给2号转盘涂上红色和黄色,使指针停在红色的可能性大于黄色。
(3)给3号转盘涂上两种颜色,使指针停在两种颜色的可能性小于灰色。
25.设计图形。
26.利用空白转盘设计一个实验,使指针停在红色区域的可能性是停在黄色区域的2倍。
六、解答题
27.将分别写着数字1、2、3、4、5、6、7、8、9的卡片反扣在桌面上,下图是李丽和张玲的对话。
(1)这个游戏规则公平吗?为什么?
(2)请设计一个对双方都公平的游戏规则。
28.有一些装有球的盒子,3个小朋友每人摸了30次,并作了记录.请你猜一猜,他们分别摸的是哪个盒子里的球?用线连一连.
29.盒子中装有三种颜色的球一共7个,同学们轮流从盒子中摸出1个球,作记录后再放回盒内。摸出球的颜色与次数统计如下:
颜色 白色 黄色 红色 蓝色
次数 48 12 24 0
盒子中装了哪几种颜色的球?
30.芳芳和丽丽做摸球游戏,每次从盒子里任意摸一个球,放回后摇匀,每人摸20次,记录如下。
芳芳 丽丽
颜色 白球 黑球 黄球 白球 黑球
次数 12 7 1 14 6
盒子里哪种颜色的球可能最多?哪种颜色的球可能最少?
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.D
【分析】可能性大小就是事情出现的概率,可能性=所求情况数÷总情况数;因为硬币只有正反两面,所以每一面出现的可能性都是,据此解答。
【详解】1÷2=
故答案为:D
【点睛】本题考查了简单事件发生的可能性的求解,注意:不要被一些无用的信息所迷惑。
2.A
【分析】首先观察转盘图可得:把这个大转盘平均分成8份,数一数哪一个图形阴影部分的份数多哪一个的可能性就大。
【详解】A.把这个大转盘平均分成8份,阴影部分是5份;
B.把这个大转盘平均分成8份,阴影部分是3份;
C.把这个大转盘平均分成8份,阴影部分是1份;
所以5>3>1,停在阴影处可能性最大的是A。
故答案为:A
【点睛】此题主要考查可能性的大小的判断。针对此题,圆的面积相等,平均分的份数相等,所以只需要看阴影的份数即可解答。
3.C
【分析】因为整个圆的面积上没有绿色的面积,所以指针不可能停在绿色面积区域。
【详解】由分析知:因为整个圆的面积上没有绿色的面积,所以指针不可能停在绿色面积区域。
故答案为:C
【点睛】解答此题根据可能性的大小进行分析,因为没有绿色的面积,所以指针不可能停在绿色面积区域。
4.B
【分析】可能性的大小与数据的多少有关系,数据越多,摸出的可能性越大,据此解答。
【详解】观察转盘可知,转盘被平均分成8份,红色有两份,白色有6份,所以停在红色区域的可能性小于其他区域,得一等奖的机会不多,偶尔可能得到。
故答案为:B。
【点睛】本题主要考查了学生对可能性大小知识的掌握情况。
5.C
【分析】必然事件指在一定条件下,一定发生的事件;
不可能事件是指在一定条件下,一定不发生的事件;
不确定事件即随机事件是指在一定条件下,可能发生也可能不发生的事件。
【详解】在一个只装有10个红球的盒子里,摸出黄球是不可能的,
因而这是一个不可能事件。
故答案为:C
【点睛】解决本题要正确理解必然事件、不可能事件、随机事件的概念;一定不发生的事件叫不可能事件。
6.C
【分析】硬币有正、反两面,抛硬币,正、反面的可能性各占一半,都有可能;属于不确定事件,但在一定条件下,可能发生,也可能不发生的事件;进而选择即可。
【详解】由分析知:抛第9次,正、反面都有可能,可能性大小相等。
故答案为:C
【点睛】解答此题应根据可能性的大小进行分析,与所抛次数无关,别被无用数字所迷惑。
7.B
【分析】因两人抛的次数相同,都是30次,“一个正方体的六个面分别标上1~6六个数”,比4大的数有两个数,小于等于4的数有4个,分别求出抛1次出现可能性,再比较即可。
因抛的次数相同,所以只比较抛一次出现的可能性的大小。
【详解】比4大的可能性:2÷6=
小于等于4的可能性:4÷6=
,所以出现大于4的可能性小。
所以小亮赢的可能性大。
故答案为:B
【点睛】本题的关键是分别求出出现大于4的和小于等于4的可能性,再进行比较。
8.C
【分析】要求转动转盘指针会偶尔指向哪个区域,也就是求指针指向哪一个颜色区域的可能性小,由图可知,黄色区域最小,所以指针会偶尔指向黄色区域;据此解答。
【详解】由图可知,黄色区域最小,所以指针会偶尔指向黄色区域。
故答案为:C
【点睛】此题考查了可能性大小的判断,所占区域面积小的可能性就小。
9. 黄 红
【分析】根据摸到不同颜色球的次数进行判断,摸到的次数多,则盒子里这种颜色的球可能多。
【详解】摸了50次,摸到红球12次,黄球38次,38>12,则根据表中的数据推测,盒子里黄色的球可能多,红色的球可能少。
【点睛】本题考查可能性的大小,根据不同颜色的球的次数即可解答。
10. 红 黄
【分析】比较两种球的数量,数量多的可能性就大。
【详解】因为球的总数不变,红球的个数多,黄球的个数少,所以任意摸出一个球,摸到红球的可能性比较大,摸到黄球的可能性较小。
【点睛】此题也可以通过计算摸到红球和黄球的可能性分别是几分之几,进而比较得解。
11.
【分析】先用“8+4”求出口袋中的袜子的总只数,求摸出红袜子和黄袜子的可能性,根据可能性的求法:即求一个数是另一个数的几分之几,用除法分别解答即可。
【详解】8+4=12(只)
8÷12=
4÷12=
答:摸出红袜子的可能性是,摸出黄袜子的可能性是;
故答案为:,。
【点睛】解答此题应根据可能性的求法:即求一个数是另一个数的几分之几用除法解答,进而得出结论。
12. 上 下
【分析】由于当翻动奇数次时,杯口向下,偶数次时,杯口向上,2008为偶数,则翻动2008次时,杯口向上,87为奇数,则当翻动87次时,杯口向下。
【详解】根据分析可知,翻动2008次杯口向上,翻动87次杯口向下。
【点睛】由“一个茶杯杯口向上放在桌子上,翻动1次杯口朝下,翻动2次杯口朝上”,得出“翻动奇数次时,杯口向下,偶数次时,杯口向上”,是解答此题的关键。
13. 口香糖 手套
【分析】任意摸出的一个球,数量多的被摸到的可能性要大,数量少的可能性就小,由此可知:在1到10这10个数字中,小于10的偶数有2、4、6、8,共4个数字;是5的倍数的数有5、10,共2个数字;既是奇数又是合数的数有9,共1个;据此可知,顾客得到口香糖的可能性最大,得到手套的可能性最小。
【详解】4>2>1
所以,顾客得到口香糖的可能性最大,得到手套的可能性最小。
【点睛】本题考查了可能性问题,每种球都有被模到的可有性,数量多的,摸到的可能性较大,反之,就少。
14. 红 蓝色或绿
【分析】哪个区域的面积大,停在哪个区域的可能性就大,哪个区域的面积小,停在哪个区域的可能性就小;把转盘平均分成4份,红色是2份,指针停在红色区域的可能性最大;蓝色和绿色都是1份,停在蓝色或绿色区域的可能性最小。
【详解】根据分析可知,转动转盘,指针停在红色区域的可能性最大;停在蓝色或绿色区域的可能性最小。
【点睛】本题考查了可能性问题,两种球都有被模到的可有性,数量多的,摸到的可能性较大,反之,就少。
15.不可能
【分析】因为盒子里有3个白球和5个红球,没有蓝球,任意摸出一个,不可能是蓝球,属于确定事件中的不可能事件,据此解答。
【详解】把3个白球和5个红球放在盒子里,任意摸出一个,不可能是蓝色的。
【点睛】考查了对事情发生的确定性与不确定性进行分析。
16.①④
【详解】略
17.×
【分析】因为盒子里共有99个红球,1个白球,则共有100个球;任意摸一个球,白球摸到的概率为总球数的,白球摸到的概率很小,但也有可能;进而得出问题答案。
【详解】由分析可知,一个盒里装有99个红球,1个白球,从盒子里任意摸出一个球,不可能摸出白球,说法错误。
故答案为:×
【点睛】此题应根据题中给出的数据进行分析,先算出这白球所占的概率是多少,进而得出正确的判断。
18.√
【分析】比较摸出哪种球的次数多,那么这种球就可能多一些。
【详解】16比4多得多,那么盒子里红球可能多一些,原题说法正确。
故答案为:√
19.√
【详解】略
20.×
【详解】略
21.
【详解】略
22.见详解
【分析】根据题意,根据可能性的大小进行分析;摸到黑球和白球的可能性一样大,那么黑球和白球的数量要相等;摸到的一定是黑球,说明袋子中都是黑球;摸到的一定是白球,说明袋子中的都是白球;摸到黑球的可能性小写,说明袋子的黑球的数量比白球的数量少;摸到黑球的可能性大一些,说明袋子中的黑球数量比白球多些,据此解答。
【详解】(1)10个白球摸到是白球的可能性为1;
(2)5个白球、5个黑球摸到黑球和白球的可能性均为;
(3)10个黑球摸到是黑球的可能性为1;
(4)8个白球、2个黑球摸到是白球的可能性为,摸到是黑球的可能性为;
(5).6个黑球、4个白球摸到是白球的可能性为,摸到是黑球的可能性为。
【点睛】本题考查可能性的大小,根据求一个数是另一个数的几分之几,进行解答。
23.见详解
【分析】(1)从10个红球里面,只能摸出红球,所以应连“一定是红球”;
(2)有5个黄球、5个红球,因为黄球和红球的个数同样多,所以应连“有可能是红,也有可能是黄”;
(3)从10个黄球里面,只能摸出黄球,所以应连“一定不是红”;
(4)从8个黄球和2个红球里面,可能摸出红球也可能摸出黄球,但由于黄球数量多,所以应连“红的可能性小”。
【详解】见下图:
【点睛】本题考查了确定事件和不确定事件,用到的知识点为:必然事件是指在一定条件下,一定发生的事件;不可能事件是指在一定条件下,一定不发生的事件;
不确定事件即随机事件是指在一定条件下,可能发生也可能不发生的事件。
24.
【详解】略
25.
【解析】略
26.见详解
【分析】把此转盘平均分成6份,使指针停在红色区域的可能性是停在黄色区域的2倍,只要使黄色区域的面积占其中的2份,红色区域的面积占其中的4份即可。
【详解】见下图:
【点睛】解决此题只要使黄色区域的面积占其中的2份,红色区域的面积占其中的4份即可。
27.(1)不公平;理由见详解;
(2)摸到比5大的数李丽赢;摸到比5小的数张玲赢。
【分析】(1)根据奇数、偶数的定义,分别找出1、2、3、4、5、6、7、8、9中奇数与偶数的个数,比较即可判断;(2)使游戏双方获胜的可能性相同即可。
【详解】(1)奇数有:1、3、5、7、9,共5个;
偶数有:2、4、6、8,共4个;
所以摸到奇数、偶数的可能性不同,这个游戏不公平。
(2)比5大的数有4个,比5小的数也有4个,可设定规则为:摸到比5大的数李丽赢;摸到比5小的数张玲赢(答案合理即可)。
【点睛】确定一个游戏是否公平,要先找出事件发生的所有可能,然后看对于游戏双方,获胜的可能性是否相同。若相同,则游戏规则公平;若不相同,则游戏规则不公平。
28.如下:
【分析】根据记录表可知,第一个小朋友摸出红球的可能性大;第二个小朋友摸出白球的可能性大,第三个小朋友摸出红球与白球的可能性差不多;根据求可能性的方法,分别求出这三个盒子中摸出红球与白球的可能性大小,再与已知的记录表比较即可解答.
【详解】每个盒子都是10个球,
第一个盒子有9个白球,所以摸出白球的可能性大,摸出红球的可能性小;
第二个盒子有5个白球5个红球,摸出红球与白球的可能性一样大;
第三个盒子有9个红球,所以摸出红球可能性大,摸出白球的可能性小,据此连线如下:
29.白,黄,红
【分析】从摸出各种颜色球的次数看,盒子里有白球、黄球、红球,没有蓝色的球。
【详解】答:盒子里装了:白色、黄色、红色三种颜色的球。
【点睛】根据可能性大小的知识,解答此题即可。
30.白球;黄球
【分析】可能性表示所求情况的数量占情况总数的几分之几,即可能性=所求事件可能发生的次数÷所有事件可能发生的次数,故出现次数多的可能就多,反之就少;题中通过两人摸球的数据分析可知,白球出现的次数最多,黄球出现的次数最少,因此可以判断白球的数量最多,黄球的数量最少,黑球介于之间。
【详解】根据分析可知,盒子里白色的球可能最多,黄色的球可能最少。
答:盒子里白球的可能最多,黄球可能最少。
【点睛】本题考查主要考查不确定事件中可能性大小的求解方法的灵活运用。
答案第1页,共2页
答案第1页,共2页
同课章节目录
- 一 小数除法
- 1 精打细算
- 2 打扫卫生
- 3 谁打电话的时间长
- 4 人民币兑换
- 5 除得尽吗
- 6 调查“生活垃圾”
- 二 轴对称和平移
- 1 轴对称再认识(一)
- 2 轴对称再认识(二)
- 3 平移
- 4 欣赏与设计
- 三 倍数与因数
- 1 倍数与因数
- 2 探索活动:2、5的倍数的特征
- 3 探索活动:3的倍数的特征
- 4 找因数
- 5 找质数
- 四 多边形的面积
- 1 比较图形的面积
- 2 认识底和高
- 3 探索活动:平行四边形的面积
- 4 探索活动:三角形的面积
- 5 探索活动:梯形的面积
- 五 分数的意义
- 1 分数的再认识(一)
- 2 分数的再认识(二)
- 3 分饼
- 4 分数与除法
- 5 分数基本性质
- 6 找最大的公因数
- 7 约分
- 8 找最小的公倍数
- 9 分数的大小
- 六 组合图形的面积
- 1 组合图形的面积
- 2 探索活动:成长的脚印
- 3 公顷、平方千米
- 数学好玩
- 1 设计秋游方案
- 2 图形中的规律
- 3 尝试与猜测
- 七 可能性
- 1 谁先走
- 2 摸球游戏
