人教版七年级上册1.2.4绝对值 (第1课时)说课课件(共14张PPT)
文档属性
| 名称 | 人教版七年级上册1.2.4绝对值 (第1课时)说课课件(共14张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 968.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-18 12:53:42 | ||
图片预览





文档简介
(共14张PPT)
1.2.4 绝对值
第1课时
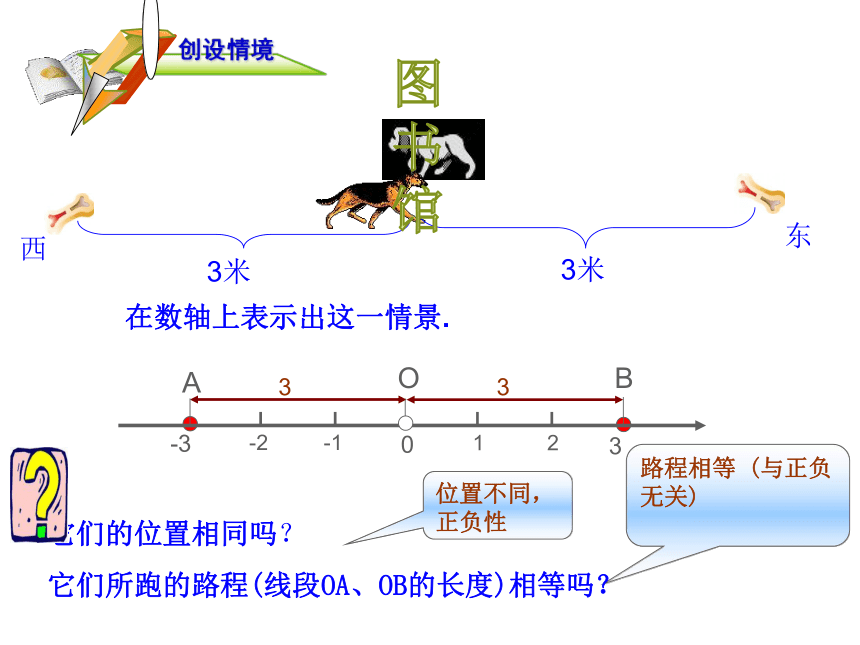
西
东
3
3
A
O
B
0
3
-3
1
2
-2
-1
3米
3米
位置不同,正负性
路程相等 (与正负无关)
它们的位置相同吗?
它们所跑的路程(线段OA、OB的长度)相等吗?
在数轴上表示出这一情景.
创设情境
图书馆
结合实际:
实际生活中,有哪些问题只关注量的具体值,而与正负无关?
出租车收费与方向无关和路程有关
引出课题:绝对值
从数轴可以发现:点A:10到原点的距离是多少,点B:—10到原点的距离是多少?观察归纳:在数轴上,互为相反数(0除外)的两个点有什么特征?
(位于原点两侧,并到原点的距离相等。)
合作探究
0
2
4
8
6
-6
10
-2
-4
-8
-10
A
B
0
6
-1
-2
-3
-4
-5
-6
1
2
3
4
5
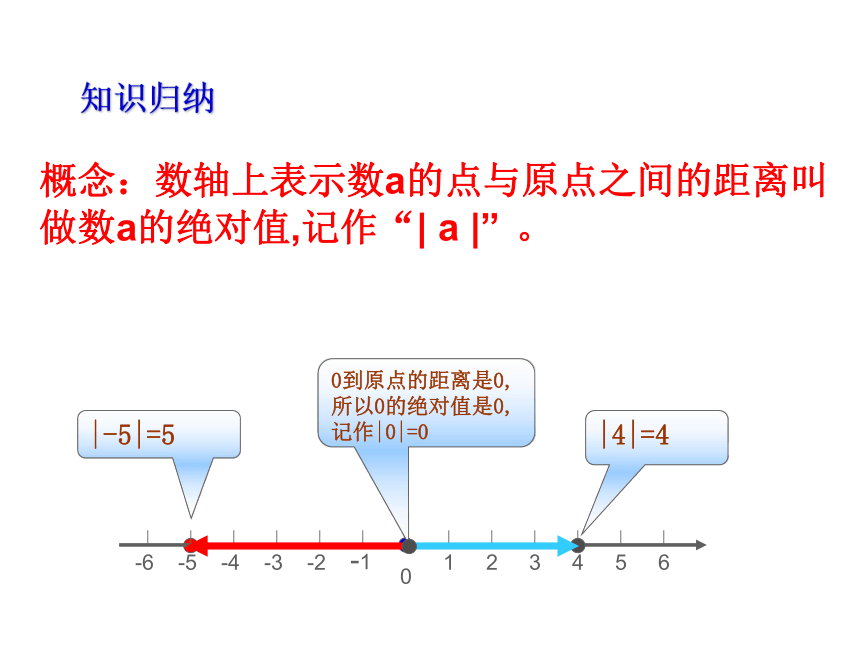
|4|=4
|-5|=5
概念:数轴上表示数a的点与原点之间的距离叫做数a的绝对值,记作“| a |” 。
0到原点的距离是0,所以0的绝对值是0,记作|0|=0
知识归纳
被点到名字的同学说出上一位同学给出数据的绝对值,并出题和点出下一位的名字
练习一、
正数的绝对值是它本身
(1)当a是正数时,|a|=____;
(2)当a是负数时,|a|=__;
(3)当a=0时,|a|=___。
a
-a
0
0的绝对值是0
负数的绝对值是它的相反数
任何一个有理数的绝对值都是非负数!
|a|≥0
若字母a表示一个有理数,你知道a的绝对值等于什么吗 (请同学们自己带一些正数、负数求出绝对值,完成填空)
议一议
练习二、 求绝对值等于4的数
解:因为数轴上到原点的距离等于4个单位长度的点有两个,是表示4的点和表示-4的点,所以绝对值等于4的数是4和-4。
精讲点拨
老师,我来!
巩固练习
1、求下列各数的绝对值。
-19,0,-2.3,-6,
2、判断
(1)一个数的绝对值一定是正数。 ( )
(2) 一个数的绝对值越大,表示它的点在
数轴上离原点越近。 ( )
(3)当a≠0时, |a|总是大于0 。 ( )
3、若|x|=5,则x为 , 若|x|=| -5|,则x为 。
4、 一个数的绝对值是它本身,那么这个数一定是 。
×
√
×
+5和-5
+5和-5
正数和零
互为相反数的两个数的绝对值相等。
能力提高
1、若|a|= - a,则a是( )
A.负数 B.正数 C.非负数 D.非正数
2、有理数a、b、c在数轴上的位置如图所示,
化简-|a|+|b|-|0|-|c|
课堂 小结
驶向胜利的彼岸
绝对值
我的收获是 … …
我感受到了… …
我的问题存在于… …
小结
1你获得那些知识?
一般地数轴上表示数a的点与原点的距离叫做数a的绝对值,记作|a|。
这里的数a可以是正数、负数和0
一个正数的绝对值是 它本身, 一个负数的绝对值是它的相反数 0的绝对值是0
(1)当a是正数时,|a|=a
(2)当a是负数时,|a|=-a
(3)当a是0时,|a|=0
作业布置
必做题:1、练习2:正式排球比赛对所用的排球重量是有严格规定的,现检查5个排球的重量,超过规定重量的克数记作正数,不足规定重量的克数记作负数,检查结果如下:
+5 -3.5 +0.7 -2.5 -0.6
问题:指出哪个排球的质量好一些,并用绝对值的知识加以说明。
2、练习册绝对值第一课时
选做题:15页拓广探究第12题
体现分层教学因材施教的教学原理。
谢谢大家!
1.2.4 绝对值
第1课时
西
东
3
3
A
O
B
0
3
-3
1
2
-2
-1
3米
3米
位置不同,正负性
路程相等 (与正负无关)
它们的位置相同吗?
它们所跑的路程(线段OA、OB的长度)相等吗?
在数轴上表示出这一情景.
创设情境
图书馆
结合实际:
实际生活中,有哪些问题只关注量的具体值,而与正负无关?
出租车收费与方向无关和路程有关
引出课题:绝对值
从数轴可以发现:点A:10到原点的距离是多少,点B:—10到原点的距离是多少?观察归纳:在数轴上,互为相反数(0除外)的两个点有什么特征?
(位于原点两侧,并到原点的距离相等。)
合作探究
0
2
4
8
6
-6
10
-2
-4
-8
-10
A
B
0
6
-1
-2
-3
-4
-5
-6
1
2
3
4
5
|4|=4
|-5|=5
概念:数轴上表示数a的点与原点之间的距离叫做数a的绝对值,记作“| a |” 。
0到原点的距离是0,所以0的绝对值是0,记作|0|=0
知识归纳
被点到名字的同学说出上一位同学给出数据的绝对值,并出题和点出下一位的名字
练习一、
正数的绝对值是它本身
(1)当a是正数时,|a|=____;
(2)当a是负数时,|a|=__;
(3)当a=0时,|a|=___。
a
-a
0
0的绝对值是0
负数的绝对值是它的相反数
任何一个有理数的绝对值都是非负数!
|a|≥0
若字母a表示一个有理数,你知道a的绝对值等于什么吗 (请同学们自己带一些正数、负数求出绝对值,完成填空)
议一议
练习二、 求绝对值等于4的数
解:因为数轴上到原点的距离等于4个单位长度的点有两个,是表示4的点和表示-4的点,所以绝对值等于4的数是4和-4。
精讲点拨
老师,我来!
巩固练习
1、求下列各数的绝对值。
-19,0,-2.3,-6,
2、判断
(1)一个数的绝对值一定是正数。 ( )
(2) 一个数的绝对值越大,表示它的点在
数轴上离原点越近。 ( )
(3)当a≠0时, |a|总是大于0 。 ( )
3、若|x|=5,则x为 , 若|x|=| -5|,则x为 。
4、 一个数的绝对值是它本身,那么这个数一定是 。
×
√
×
+5和-5
+5和-5
正数和零
互为相反数的两个数的绝对值相等。
能力提高
1、若|a|= - a,则a是( )
A.负数 B.正数 C.非负数 D.非正数
2、有理数a、b、c在数轴上的位置如图所示,
化简-|a|+|b|-|0|-|c|
课堂 小结
驶向胜利的彼岸
绝对值
我的收获是 … …
我感受到了… …
我的问题存在于… …
小结
1你获得那些知识?
一般地数轴上表示数a的点与原点的距离叫做数a的绝对值,记作|a|。
这里的数a可以是正数、负数和0
一个正数的绝对值是 它本身, 一个负数的绝对值是它的相反数 0的绝对值是0
(1)当a是正数时,|a|=a
(2)当a是负数时,|a|=-a
(3)当a是0时,|a|=0
作业布置
必做题:1、练习2:正式排球比赛对所用的排球重量是有严格规定的,现检查5个排球的重量,超过规定重量的克数记作正数,不足规定重量的克数记作负数,检查结果如下:
+5 -3.5 +0.7 -2.5 -0.6
问题:指出哪个排球的质量好一些,并用绝对值的知识加以说明。
2、练习册绝对值第一课时
选做题:15页拓广探究第12题
体现分层教学因材施教的教学原理。
谢谢大家!
