人教版九年级上册 22.1.2 二次函数的图像与性质课件(共129张PPT)
文档属性
| 名称 | 人教版九年级上册 22.1.2 二次函数的图像与性质课件(共129张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 5.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-18 13:18:37 | ||
图片预览








文档简介
(共130张PPT)
第二十二章 二次函数
……本章主要内容……
22.1 二次函数的图像和性质
22.1 二次函数的图像和性质
基础回顾 什么叫函数
在某变化过程中的两个变量x、y,当变量x在某个范围内取一个确定的值,另一个变量y总有唯一的值与它对应。
这样的两个变量之间的关系我们把它叫做函数关系。
对于上述变量x 、y,我们把y叫x的函数。 x叫自变量, y叫应变量。
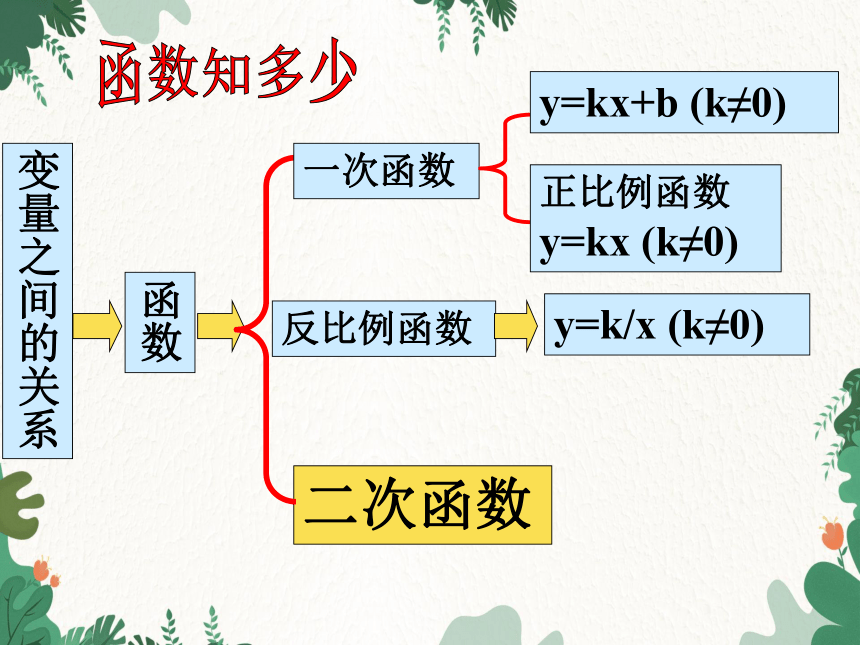
目前,我们已经学习了那几种类型的函数?
二次函数
变量之间的关系
函数
一次函数
反比例函数
y=kx+b (k≠0)
正比例函数y=kx (k≠0)
y=k/x (k≠0)
节日的喷泉给人带来喜庆,你是否注意过水流所经过的路线?它会与某种函数有联系吗?
奥运赛场腾空的篮球
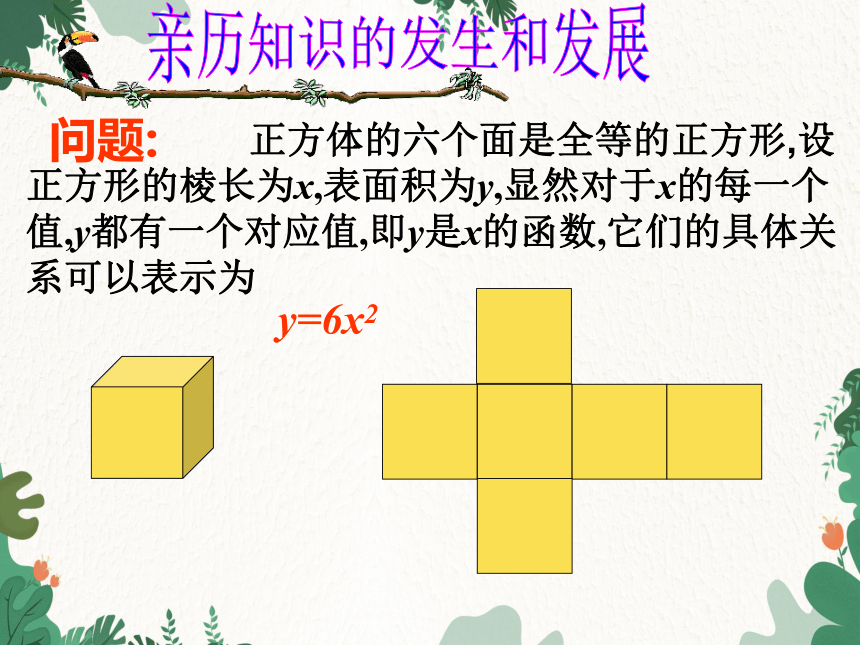
正方体的六个面是全等的正方形,设正方形的棱长为x,表面积为y,显然对于x的每一个值,y都有一个对应值,即y是x的函数,它们的具体关系可以表示为
问题:
y=6x2
函数①②③有什么共同点
观察:
y=6x2①
在上面的问题中,函数都是用自变量的二次式表示的。
定义:一般地,形如y=ax +bx+c(a,b,c是常数,a≠ 0)的函数叫做二次函数。其中x是自变量,a为二次项系数,ax2叫做二次项,b为一次项系数,bx叫做一次项,c为常数项。
(1)等号左边是变量y,右边是关于自变量 x的
(3 )等式的右边最高次数为 ,可以没有一次 项和常数项,但不能没有二次项。
注意:
(2)a,b,c为常数,且
(4)x的取值范围是任意实数。
整式。
a≠0.
2
(5)函数的右边是一个 整 式。
二次函数的一般形式:
y=ax2+bx+c (其中a、b、c是常数,a≠0)
二次函数的特殊形式:
当b=0时, y=ax2+c
当c=0时, y=ax2+bx
当b=0,c=0时, y=ax2
1、 说出下列二次函数的二次项系数、一次项系
数、常数项
(1) y=-x2+58x-112
(2)y=πx2
2、指出下列函数y=ax +bx+c中的a、b、c
(1) y=-3x2-x-1
(3) y=x(1+x)
(2) y=5x2-6
例1、下列函数中,哪些是二次函数?若是,分别指出二次项系数,一次项系数,常数项。
(1) y=3(x-1) +1 (2) y=x+
(3) s=3-2t (4) y=(x+3) -x
(5)y= -x (6) v=8π r
1
x
__
x
1
__
思考:2. 二次函数的一般式y=ax2+bx+c(a≠0)与一元二次方程ax2+bx+c=0(a≠0)有什么联系和区别?
驶向胜利的彼岸
联系(1)等式一边都是ax2+bx+c且 a ≠0 (2)方程ax2+bx+c=0可以看成是函数y= ax2+bx+c中y=0时得到的.
区别:前者是函数.后者是方程.等式另一边前者是y,后者是0
知识运用
例1:下列函数中,哪些是二次函数?
(1)y=3x-1 ( ) (2)y=3x2 ( )
(3)y=3x3+2x2 ( ) (4)y=2x2-2x+1( )
(5)y=x-2+x ( ) (6)y=x2-x(1+x) ( )
不是
是
不是
不是
是
不是
知识运用
m2—2m-1=2 m+1 ≠0 ∴m=3
例2:m取何值时, 函数y= (m+1)x
+(m-3)x+m 是二次函数?
解:由题意得
一次函数y=kx+b (k ≠0),其中包括正比例函数 y=kx(k≠0),
反比例函数y= (k≠0) ,
二次函数y=ax2+bx+c(a≠0)。
现在我们学习过的函数有:
可以发现,这些函数的名称都形象地反映了函数表达式与自变量的关系。
想一想
例2、y=(m+3)x
(1)m取什么值时,此函数是正比例函数?
(2) m取什么值时,此函数是反比例函数?
(3) m取什么值时,此函数是二次函数?
m2-7
解:(1)当m2-7=1且m+3≠0即m=± 时是正比例函数。
(2)当m2-7=-1且m+3≠0即m=± 时是反比例函数。
(3)当m2-7=2且m+3≠0即m=3时是二次函数。
1.一个圆柱的高等于底面半径,写出它的表面积 s 与半径 r 之间的关系式.
2. n支球队参加比赛,每两队之间进行一场比赛,写出比赛的场次数 m与球队数 n 之间的关系式.
S=2πr2 +2πr2 即S=4πr2
即
3、下列函数中,(x是自变量),是二次函数的有 。
A y=ax2+bx+c B y2=x2-4x+1
C y=x2 D y=2+ √x2+1
4.函数 y=(m-n)x2+ mx+n 是二次函数的条件是( )
A m,n是常数,且m≠0 B m,n是常数,且n≠0
C m,n是常数,且m≠n D m,n为任何实数
B C
C
一农民用40m长的篱笆围成一个一边靠墙的长方形菜园,和墙垂直的一边长为Xm,菜园的面积为Ym2,求y与x之间的函数关系式,并说出自变量的取值范围。当x=12m时,计算菜园的面积。
xm
y m2
xm
(40-2x )m
解:
由题意得:
Y=x(40-2x)
即:Y=-2x2+40x
(0当x=12m时,菜园的面积为:
Y=-2x2+40x=-2×122+40×12
=192(m2)
多边形的对角线数d与边数n有什么关系?
问题2:
由图可以想出,如果多边形有n条边,那么它有 个顶点,从一个顶点出发,连接与这点不相邻的各顶点,可以作 条
对角线.
n
(n-3)
因为像线段MN与NM那样,连接相同两顶点的对角线是同一条对角线,所以多边形的对角线总数
M
N
即
在实践中感悟
横看成岭侧成峰,远近高低各不同
——变换角度分析问题
若函数y=x2m+n - 2xm-n+3是以x为自变量的二次函数,求m、n的值。
① ② ③ ④ ⑤
∵
2m+n=2
m-n=1
∴ m=1
n=0
∵
∴
2m+n=1
m-n=2
m=1
n=-1
∵
∴
2m+n=2
m-n=2
m=4/3
n=-2/3
∵
∴
2m+n=2
m-n=0
m=2/3
n=-4/3
∵
∴
2m+n=0
m-n=2
m=2/3
n=2/3
22.1 二次函数的图像和性质
1、一次函数的图像有何特征?
一次函数的图像是一条 。
当 时,y随x的增大而增大;
当 时,y随x的增大而减小。
2、反比例函数的图像有何特征?
反比例函数的图像是 ,共有 支,且关于 对称。
当 时,图像在 象限,在每个象限内y随x的增大而减小;
当 时,图像在 象限,在每个象限内y随x的增大而 。
直线
双曲线
两
原点
增大
一、三
二、四
k>0
k>0
k<0
k<0
3、画函数图像的基本步骤是:
、 、 。
列表
描点
连线
…二次函数的图像和性质…
y=ax2的函数图像
y=ax2 +k 的函数图像
y=a(x-h)2的函数图像
y=a(x-h)2 +k 的函数图像
y=ax2+bx+c 的函数图像
…二次函数的图像和性质…
y=ax2的函数图像
y=ax2 +k 的函数图像
y=a(x-h)2的函数图像
y=a(x-h)2 +k 的函数图像
y=ax2+bx+c 的函数图像
画形如y=ax2的函数图像:
1、画函数y=x2的图像;
观察y=x2的表达式,选择适当x值,并计算相应的y值,完成下表:
x … …
y=x2 … …
9
4
1
1
0
4
9
-3
-2
-1
0
1
2
3
x
y
0
-4
-3
-2
-1
1
2
3
4
10
8
6
4
2
-2
描点,连线
y=x2
二次函数y=x2的图象形如物体抛射时所经过的路线,我们把它叫做抛物线
二次函数 y = x2的图象是一条曲线,它的形状类似于投篮球时球在空中所经过的路线,只是这条曲线开口向上,这条曲线叫做抛物线 y = x2 ,
-3
3
3
6
9
二次函数的图象都是抛物线。
一般地,二次函数 y = ax2 + bx + c(a≠0)的图象叫做抛物线y = ax2 + bx + c
思考:这个二次函数图象有什么特征?
(1)形状是开口向上的抛物线
(2)图象关于y轴对称
(3)有最低点,没有最高点
y轴是抛物线y = x 2 的对称轴,抛物线y = x 2 与它的对称轴的交点(0,0)叫做抛物线y = x2 的顶点,它是抛物线y = x 2 的最低点.
-3
3
3
6
9
实际上,每条抛物线都有对称轴,抛物线与对称轴的交点叫做抛物线的顶点.顶点是抛物线的最低点或最高点.
思考:这个二次函数图象有什么特征?
(1)形状是开口向上的抛物线
(2)图象关于y轴对称
(3)有最低点,没有最高点
例1 在同一直角坐标系中,画出函数 的图象.
解:分别填表,再画出它们的图象,如图
x ··· -4 -3 -2 -1 0 1 2 3 4 ···
···
···
x ··· -2 -1.5 -1 -0.5 0 0.5 1 1.5 2 ···
··· ···
8
2
0.5
0
8
4.5
2
0.5
4.5
4.5
8
2
0.5
0
8
4.5
2
0.5
-2
2
2
4
6
4
-4
8
函数 的图象与函数 y=x2 的图象相比,有什么共同点和不同点?
相同点:开口都向上,顶点是原点而且是抛物线的最低点,对称轴是 y 轴
不同点:a 要越大,抛物线的开口越小.
-2
2
2
4
6
4
-4
8
你画出的图象与图中相同吗?
探究
画出函数 的图象,并考虑这些抛物线有什么共同点和不同点.
x ··· -4 -3 -2 -1 0 1 2 3 4 ···
···
···
x ··· -2 -1.5 -1 -0.5 0 0.5 1 1.5 2 ···
··· ···
-8
-4.5
-2
-0.5
0
-8
-4.5
-2
-0.5
-8
-4.5
-2
-0.5
0
-8
-4.5
-2
-0.5
-2
2
-2
-4
-6
4
-4
-8
对比抛物线,y=x2和y=-x2.它们关于x轴对称吗?一般地,抛物线y=ax2和y=-ax2呢?
一般地,抛物线 y=ax2 的对称轴是_____,顶点是______.
当a>0时,抛物线的开口______,顶点是抛物线的最______点,a越大,抛物线的开口越_______;
当a<0时,抛物线的开口_______,顶点是抛物线的最________点,a越大,抛物线的开口越_________.
向下
高
大
练习:
函数 的图象是 ,顶点坐标是 ,对称轴是 ,开口方向是 .
y轴
原点
向上
低
小
3、试说出函数y=ax2(a是常数,a≠0)的图象的开口方向、对称轴和顶点坐标,并填写下表.
y=ax2
向上
向下
y轴
y轴
(0,0)
(0,0)
|a|越大开口越小, |a|越小开口越大。
反馈测试
抛物线y=4x2中的开口方向是 ,顶点坐标是 ,对称轴是 .
抛物线 y= -
x2 的开口方向是 ,顶点坐标是 , 对称轴是 .
3. 二次函数y=ax2与y=2x2,开口大小,形状一样,开口方向相反,则a= .
…二次函数的图像和性质…
y=ax2的函数图像
y=ax2 +k 的函数图像
y=a(x-h)2的函数图像
y=a(x-h)2 +k 的函数图像
y=ax2+bx+c 的函数图像
1.二次函数y=2x2的图象是____,它的开口向_____,顶点坐标是_____;对称轴是______,在对称轴的左侧,y随x的增大而______,在对称轴的右侧,y随x的增大而______,函数y=2x2当x=______时, y有最______值,其最______值是______。
课前复习
2、二次函数 y=2x 、 的图象与二次函数 y=x 的图象有什么相同和不同?
a>0
O
x
y
1
2
3
4
5
1
2
3
4
5
–5
–4
–3
–2
–1
–5
–4
–3
–2
–1
a<0
3、试说出函数y=ax2(a是常数,a≠0)的图象的开口方向、对称轴和顶点坐标,并填写下表.
y=ax2
向上
向下
y轴
y轴
(0,0)
(0,0)
4、二次函数y=2x2+1的图象与二次函数y=2x2的图象开口方向、对称轴和顶点坐标是否相同 它们有什么关系?我们应该采取什么方法来研究这个问题?
画出函数y=2x2和函数y= 2x2+1的图象,并加以比较
(1)二次函数 y=2x +1 的图象与二次函数 y=2x 的图象有什么关系?
x … –1.5 –1 –0.5 0 0.5 1 1.5 …
y=2x2 … 4.5 2 0.5 0 0.5 2 4.5 …
y=2x2+1 … 5.5 3 1.5 1 1.5 3 5.5 …
(0,1)
x … –1.5 –1 –0.5 0 0.5 1 1.5 …
y=2x2 … 4.5 2 0.5 0 0.5 2 4.5 …
y=2x2+1 … 5.5 3 1.5 1 1.5 3 5.5 …
(0,1)
问题1:当自变量x取同一数值时,这两个函数的函数值之间有什么关系 反映在图象上,相应的两个点之间的位置又有什么关系
2、函数y=2x2+1的图象可以看成是将函数y=2x2的图象向上平移一个单位得到的。
1、函数y=2x2+1与y=2x2的图象开口方向、对称轴相同,但顶点坐标不同,函数y= 2x2的图象的顶点坐标是(0,0),而函数y=2x2+1的图象的顶点坐标是(0,1)。
函数y=2x2+1和y=2x2的图象有什么联系
你能由函数y=2x2的性质,得到函数y=2x2+1的一些性质吗
完成填空:
当x______时,函数值y随x的增大而减小;当x______时,函数值y随x的增大而增大,当x______时,函数取得最______值,最______值y=______.
以上就是函数y=2x2+1的性质。
﹥0
﹤0
=0
小
小
1
(2)二次函数 y=3x -1 的图象与二次函数 y=3x 的图象有什么关系?
x … –1 –0.6 –0.3 0 0.3 0.6 1 …
y=3x2 … 3 1.08 0.27 0 0.27 1.08 3 …
y=3x2–1 … 2 0.08 –0.73 – 1 –0.73 0.08 2 …
(0,-1)
a>0
(3)在同一直角坐标系中画出函数
的图像
O
x
y
1
2
3
4
5
1
2
3
4
5
–5
–4
–3
–2
–1
–5
–4
–3
–2
–1
y
在同一直角坐标系中画出函数
的图像
a<0
(0,2)
(0,-2)
试说出函数y=ax2+k(a、k是常数,a≠0)的图象的开口方向、对称轴和顶点坐标,并填写下表.
向上
向下
y轴
y轴
(0,k)
(0,k)
|a|越大开口越小,反之开口越大。
练习
1.把抛物线 向下平移2个单位,可以得到抛物线 ,再向上平移5个单位,可以得到抛物线 ;
2.对于函数y= –x2+1,当x 时,函数值y随x的增大而增大;当x 时,函数值y随x的增大而减小;当x 时,函数取得最 值,为 。
<0
>0
=0
大
0
3.函数y=3x2+5与y=3x2的图象的不同之处是( )
A.对称轴 B.开口方向 C.顶点 D.形状
4.已知抛物线y=2x2–1上有两点(x1,y1 ) ,(x2,y2 )且x1<x2<0,则y1 y2(填“<”或“>”)
5.已知抛物线 ,把它向下平移,得到的抛物线与x轴交于A、B两点,与y轴交于C点,若⊿ABC是直角三角形,那么原抛物线应向下平移几个单位?
C
…二次函数的图像和性质…
y=ax2的函数图像
y=ax2 +k 的函数图像
y=a(x-h)2的函数图像
y=a(x-h)2 +k 的函数图像
y=ax2+bx+c 的函数图像
y=ax2+k a>0 a<0
图象
开口
对称性
顶点
增减性
二次函数y=ax2+k的性质
开口向上
开口向下
a的绝对值越大,开口越小
关于y轴对称
顶点是最低点
顶点是最高点
在对称轴左侧递减
在对称轴右侧递增
在对称轴左侧递增
在对称轴右侧递减
k>0
k<0
k<0
k>0
(0,k)
x … -3 -2 -1 0 1 2 3 …
解:列表
画出二次函数 、 的图像,并考虑它们的开口方向、对称轴和顶点.
-2
…
0
-0.5
-2
-0.5
-8
…
-4.5
-8
…
-2
-0.5
0
-4.5
-2
…
-0.5
1
2
3
4
5
x
-1
-2
-3
-4
-5
-6
-7
-8
-9
1
y
o
-1
-2
-3
-4
-5
-10
x=-1
抛物线 与 的开口方向、对称轴、顶点
抛物线 与
抛物线
有什么关系
1
2
3
4
5
x
-1
-2
-3
-4
-5
-6
-7
-8
-9
1
y
o
-1
-2
-3
-4
-5
-10
1
2
3
4
5
x
-1
-2
-3
-4
-5
-6
-7
-8
-9
1
y
o
-1
-2
-3
-4
-5
-10
向左平移1个单位
向右平移1个单位
在同一坐标系中作出下列二次函数:
观察三条抛物线的相互关系,并分别指出它们的开口方向,对称轴及顶点.
顶点(0,0)
顶点(2,0)
直线x=-2
直线x=2
向右平移2个单位
向左平移2个单位
顶点(-2,0)
对称轴:y轴
即直线: x=0
在同一坐标系中作出下列二次函数:
观察三条抛物线的相互关系,并分别指出它们的开口方向,对称轴及顶点.
向右平移2个单位
向右平移2个单位
向左平移2个单位
向左平移2个单位
一般地,抛物线y=a(x-h)2有如下特点:
(1)对称轴是x=h;
(2)顶点是(h,0).
(3)抛物线y=a(x-h)2可以由抛物线y=ax2向左或向右平移|h|得到.
h>0,向右平移;h<0,向左平移
x
y
y=a(x-h)2 a>0 a<0
图象
开口
对称性
顶点
增减性
二次函数y=a(x-h)2的性质
开口向上
开口向下
a的绝对值越大,开口越小
直线x=h
顶点是最低点
顶点是最高点
在对称轴左侧递减
在对称轴右侧递增
在对称轴左侧递增
在对称轴右侧递减
h>0
h<0
h<0
h>0
(h,0)
y=-2(x+3)2
1、说出抛物线的开口方向、对称轴、顶点,最大值或最小值各是什么及增减性如何?
y=2(x-3)2
y=-2(x-2)2
y=3(x+1)2
2、若将抛物线y=-2(x-2)2的图象的顶点移到原点,则下列平移方法正确的是( )
A、向上平移2个单位
B、向下平移2个单位
C、向左平移2个单位
D、向右平移2个单位
C
3、抛物线y=4(x-3)2的开口方向 ,对称轴是 ,顶点坐标是 ,抛物线是最 点,
当x= 时,y有最 值,其值为 。
抛物线与x轴交点坐标 ,与y轴交点坐标 。
向上
直线x=3
(3,0)
低
3
小
0
(3,0)
(0,36)
4.用配方法把下列函数化成y=a(x-h)2的形式,并说出开口方向,顶点坐标和对称轴。
5、按下列要求求出二次函数的解析式:
(1)已知抛物线y=a(x-h)2经过点
(-3,2)(-1,0)求该抛物线线的解析式。
(2)形状与y=-2(x+3)2的图象形状相同,但开口方向不同,顶点坐标是(1,0)的抛物线解析式。
(3)已知二次函数图像的顶点在x轴上,且图像经过点(2,-2)与(-1,-8)。求此函数解析式。
抛物线 开口方向 对称轴 顶点坐标
y = 2(x+3)2
y = -3(x-1)2
y = -4(x-3)2
向上
直线x=-3
( -3 , 0 )
直线x=1
直线x=3
向下
向下
( 1 , 0 )
( 3, 0)
3.抛物线y=ax2+k有如下特点:
当a>0时, 开口向上;
当a<0时,开口向上.
(2)对称轴是y轴;
(3)顶点是(0,k).
抛物线y=a(x-h)2有如下特点:
(1)当a>0时, 开口向上,当a<0时,开口向上;
(2)对称轴是x=h;
(3)顶点是(h,0).
2.抛物线y=ax2+k可以由抛物线y=ax2向上或向下平移|k|得到.
抛物线y=a(x-h)2可以由抛物线y=ax2向左或向右平移|h|得到.
(k>0,向上平移;k<0向下平移.)
(h>0,向右平移;h<0向左平移.)
1.抛物线y=ax2+k、抛物线y=a(x-h)2和抛物线y=ax2的形状完全相同,开口方向一致;
(1)当a>0时, 开口向上,当a<0时,开口向下;
如何平移:
…二次函数的图像和性质…
y=ax2的函数图像
y=ax2 +k 的函数图像
y=a(x-h)2的函数图像
y=a(x-h)2 +k 的函数图像
y=ax2+bx+c 的函数图像
在同一坐标系中作出二次函数y=3x2和y=3(x-1)2的图象.观察图象,回答问题
(1)函数y=3(x-1)2的图象与y=3x2的图象有什么关系 它是轴对称图形吗 它的对称轴和顶点坐标分别是什么
(2)x取哪些值时,函数y=3(x-1)2的值随x值的增大而增大 x取哪些值时,函数y=3(x-1)2的值随x的增大而减少?
在同一坐标系中,作出二次函数y=3x , y=3(x-1)2和y=3(x-1)2+2的图象.
根据图象回答问题:三个图象有什么关系 它们的开口方向,对称轴和顶点坐标分别是什么
对称轴仍是平行于y轴
的直线x=1;增减性与
y=3x2类似.
顶点是(1,2).
二次函数y=3(x-1)2+2的
图象可以看作是抛物线
y=3x2先沿着x轴向右平移
1个单位,再沿直线x=1向
上平移2个单位后得到的.
开口向上,当
X=1时有最小
值:且最小值=2.
先猜一猜,再做一做,在同一坐标系中作二次函数y=3(x-1)2-2,会是什么样
X=1
对称轴仍是平行于y轴的直线
(x=1);增减性与y=3x2类似.
顶点是(1,-2)
二次函数y=3(x-1)2-2的
图象可以看作是抛物线
y=3x2先沿着x轴向右平移
1个单位,再沿直线x=1向
下平移2个单位后得到的.
二次函数y=3(x-1)2-2的图象与抛物线y=3x2和y=3(x-1)2有何关系 它的开口方向、对称轴和顶点坐标分别是什么
开口向上,
当x=1时y有
最小值:且
最小值= -2.
二次函数y=-3(x-1)2+2和y=-3(x-1)2, y=-3x 的图象有什么关系 它们的开口方向,对称轴和顶点坐标分别是什么 再作图看一看.
X=1
在同一坐标系中,作出二次函数y=-3(x-1)2+2, y=-3(x-1)2-2, y=-3x 和
y=-3(x-1)2的图象。
根据图像
回答问题
对称轴仍是平行于y轴的直线
(x=1);增减性与y=-3x2类似.
顶点分别是
(1,2)和(1,-2).
二次函数
y=-3(x-1)2+2与y=-3(x-1)2+2的
图象可以看作是抛物线y=-3x2先沿
着x轴向右平移1个单位,再沿直线
x=1向上(或向下)平移2个单位后
得到的.
二次函数y=-3(x-1)2+2与y=-3(x-1)2-2的图象和抛物线y=-3x ,y=-3(x-1)2有什么关系 它的开口方向,对称轴和顶点坐标分别是什么
开口向下,当x=1
时y有最大值;且
最大值=2(或
最大值=-2).
想一想,二次函数y=-3(x+1)2+2与y=-3(x+1)2-2的图象和抛物线y=-3x ,y=-3(x+1)2
y
X=1
对称轴仍是平行于y轴的直线
(x=-1);增减性与y= -3x2类似.
顶点分别是
(-1,2)和(-1,-2)..
二次函数y=-3(x+1)2+2与
y=-3(x+1)2-2的图象可
以看作是抛物线y=-3x2
先沿着x轴向左平移1个
单位,再沿直线x=-1向上
(或向下)平移2个单位后
得到的.
二次函数y=-3(x+1)2+2与y=-3(x+1)2-2的图象和抛物线y=-3x ,y=-3(x+1)2有什么关系 它的开口方向,对称轴和顶点坐标分别是什么
开口向下,
当x=-1时y有
最大值:且
最大值= 2
(或最大值= - 2).
先想一想,再总结二次函数y=a(x-h)2+k的图象和性质.
x=1
一般地,由y=ax 的图象便可得到二次函数y=a(x-h) +k的图象:y=a(x-h) +k(a≠0) 的图象可以看成y=ax 的图象先沿x轴整体左(右)平移|h|个单位(当h>0时,向右平移;当h<0时,向左平移),再沿对称轴整体上(下)平移|k|个单位 (当k>0时,向上平移;当k<0时,向下平移)得到的.
因此,二次函数y=a(x-h) +k的图象是一条抛物线,它的开口方向、对称轴和顶点坐标与a,h,k的值有关.
归纳
用平移观点看函数:
抛物线 与抛物线 形状相同,位置不同.
二次函数 特点:
归纳
1.图象是一条抛物线,对称轴为直线
x=h,顶点为(h,k)。
2.当a>0时,开口向上;
当x=h时,y取最小值为k;
在对称轴的左侧,y随x的增大而减小,
在对称轴的右侧,y随x的增大而增大.
3.当a<0时,开口向下;
当x=h时,y取最大值为k;
在对称轴的左侧,y随x的增大而增大,
在对称轴的右侧,y随x的增大而减小.
二次函数y=a(x-h)2+k的图象和性质
1.顶点坐标与对称轴
2.位置与开口方向
3.增减性与最值
抛物线
顶点坐标
对称轴
位置
开口方向
增减性
最值
y=a(x-h)2+k(a>0)
y=a(x-h)2+k(a<0)
(h,k)
(h,k)
直线x=h
直线x=h
由h和k的符号确定
由h和k的符号确定
向上
向下
当x=h时,最小值为k.
当x=h时,最大值为k.
在对称轴的左侧,y随着x的增大而减小. 在对称轴的右侧, y随着x的增大而增大.
在对称轴的左侧,y随着x的增大而增大. 在对称轴的右侧, y随着x的增大而减小.
根据图形填表:
1.指出下列函数图象的开口方向对称轴和顶点坐标及最值:
3.对于二次函数y=3(x+1)2,当x取哪些值时,y的值随x值的增大而增大 当x取哪些值时,y的值随x值的增大而减小 二次函数y=3(x+1)2+4呢
2.(1)二次函数y=3(x+1)2的图象与二次函数y=3x2的图象有什么关系 它是轴对称图形吗 它的对称轴和顶点坐标分别是什么
(2)二次函数 y=-3(x-2)2+4 的图象与二次函数 y=-3x2的图象有什么关系
2.不同点: 只是位置不同(1)顶点不同:分别是(h,k)和(0,0).
(2)对称轴不同:分别是直线x= h和y轴.
(3)最值不同:分别是k和0.
3.联系: y=a(x-h) +k(a≠0) 的图象可以看成y=ax 的图象先沿x轴整体左(右)平移|h|个单位(当h>0时,向右平移;当h<0时,向左平移),再沿对称轴整体上(下)平移|k|个单位 (当k>0时向上平移;当k<0时,向下平移)得到的.
1.相同点: (1)形状相同(图像都是抛物线,开口方向相同).
(2)都是轴对称图形.
(3)都有最(大或小)值.
(4)a>0时, 开口向上,在对称轴左侧,y都随x的增大而减小,在对称轴右侧,y都随 x的增大而增大. a<0时,开口向下,在对称轴左侧,y都随x的增大而增大,在对称轴右侧,y都随 x的增大而减小 .
二次函数y=a(x-h) +k与y=ax 的关系
1.指出下列函数图象的开口方向,对称轴和顶点坐标.必要时作出草图进行验证.
2.填写下表:
y=a(x-h) +k 开口方向 对称轴 顶点坐标
a>0
a<0
…二次函数的图像和性质…
y=ax2的函数图像
y=ax2 +k 的函数图像
y=a(x-h)2的函数图像
y=a(x-h)2 +k 的函数图像
y=ax2+bx+c 的函数图像
一般地,抛物线y=a(x-h) +k与y=ax 的 相同, 不同
2
2
形状
位置
y=ax
2
y=a(x-h) +k
2
上加下减
左加右减
抛物线y=a(x-h)2+k有如下特点:
1.当a﹥0时,开口 ,
当a﹤0时,开口 ,
向上
向下
2.对称轴是 ;
3.顶点坐标是 。
直线X=h
(h,k)
二次函数 开口方向 对称轴 顶点坐标
y=2(x+3)2+5
y = -3x(x-1)2 -2
y = 4(x-3)2 +7
y = -5(2-x)2 - 6
直线x=–3
直线x=1
直线x=2
直线x=3
向上
向上
向下
向下
(-3,5)
(1,-2)
(3,7 )
(2,-6)
你能说出二次函数y=—x -6x+21图像的特征吗?
2
1
2
探究:
如何画出 的图象呢
我们知道,像y=a(x-h)2+k这样的函数,容易确定相应抛物线的顶点为(h,k), 二次函数 也能化成这样的形式吗
配方
y= — (x―6) +3
2
1
2
你知道是怎样配方的吗?
(1)“提”:提出二次项系数;
( 2 )“配”:括号内配成完全平方;
(3)“化”:化成顶点式。
归纳
二次函数 y= —x -6x +21图象的
画法:
(1)“化” :化成顶点式 ;
(2)“定”:确定开口方向、对称轴、顶
点坐标;
(3)“画”:列表、描点、连线。
2
1
2
5
10
5
10
O
x
y
x … 3 4 5 6 7 8 9 …
… 7.5 5 3.5 3 3.5 5 7.5 …
求次函数y=ax +bx+c的对称轴和顶点坐标.
函数y=ax +bx+c的顶点是
配方:
提取二次项系数
配方:加上再减去一次项系数绝对值一半的平方
整理:前三项化为平方形式,后两项合并同类项
化简:去掉中括号
这个结果通常称为求顶点坐标公式.
函数y=ax +bx+c的对称轴、顶点坐标是什么?
1. 说出下列函数的开口方向、对称轴、顶点坐标:
函数y=ax +bx+c的对称轴、顶点坐标是什么?
例1:指出抛物线:
的开口方向,求出它的对称轴、顶点坐标、与y轴的交点坐标、与x轴的交点坐标。并画出草图。
对于y=ax2+bx+c我们可以确定它的开口方向,求出它的对称轴、顶点坐标、与y轴的交点坐标、与x轴的交点坐标(有交点时),这样就可以画出它的大致图象。
方法归纳
配方法
1
公式法
2
单击添加文字内容
3
①y=2x2-5x+3
③y=(x-3)(x+2)
②y=- x2+4x-9
求下列二次函数图像的开口、顶点、对称轴
请画出草图:
3
-9
-6
抛物线位置与系数a,b,c的关系:
⑴a决定抛物线的开口方向:
a>0 开口向上
a<0 开口向下
⑵ a,b决定抛物线对称轴的位置:
(对称轴是直线x = -— )
① a,b同号<=> 对称轴在y轴左侧;
② b=0 <=> 对称轴是y轴;
③ a,b异号<=> 对称轴在y轴右侧
2a
b
【左同右异】
⑶ c决定抛物线与y轴交点的位置:
① c>0 <=>图象与y轴交点在x轴上方;
② c=0 <=>图象过原点;
③ c<0 <=>图象与y轴交点在x轴下方。
⑷顶点坐标是( , )。
(5)二次函数有最大或最小值由a决定。
当x=- — 时,y有最大(最小)值 y=
b
2a
______________________
4a
4ac-b
2
-1
例2、已知函数y = ax2 +bx +c的图象如下图所示,x= 为该图象的对称轴,根
据图象信息你能得到关于系数a,b,c的一些什么结论?
y
1
.
.
x
1
3
1.抛物线y=2x2+8x-11的顶点在 ( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
2.不论k 取任何实数,抛物线y=a(x+k)2+k(a≠0)的顶点都在 ( )
A.直线y = x上 B.直线y = - x上
C.x轴上 D.y轴上
3.若二次函数y=ax2 + 4x+a-1的最小值是2,则a的值是 ( )
A 4 B. -1 C. 3 D.4或-1
C
B
A
4.若二次函数 y=ax2 + b x + c 的图象如下,与x轴的一个交点为(1,0),则下列各式中不成立的是 ( )
A.b2-4ac>0 B. <0
C.a+b+c=0 D. >0
1
x
y
o
-1
5.若把抛物线y = x2 - 2x+1向右平移2个单位,再向下平移3个单位,得抛物线y=x2+bx+c,则( )
A.b=2 c= 6 B.b=-6 , c=6
C.b=-8 c= 6 D.b=-8 , c=18
B
B
-
2a
b
4a
4ac-b2
6.若一次函数 y=ax+b 的图象经过第二、三、四象限,则二次函数 y=ax2+bx-3 的大致图象是 ( )
7.在同一直角坐标系中,二次函数 y=ax2+bx+c 与一次函数y=ax+c的大致图象可能是 ( )
x
y
o
x
y
o
x
y
o
x
y
o
A
B
C
D
-3
-3
-3
-3
x
y
o
x
y
o
x
y
o
x
y
o
A
B
C
D
C
C
二次函数y=ax2+bx+c(a≠0)的图象和性质
1.顶点坐标与对称轴
2.位置与开口方向
3.增减性与最值
抛物线
顶点坐标
对称轴
位置
开口方向
增减性
最值
y=ax2+bx+c(a>0)
y=ax2+bx+c(a<0)
由a,b和c的符号确定
由a,b和c的符号确定
向上
向下
在对称轴的左侧,y随着x的增大而减小. 在对称轴的右侧, y随着x的增大而增大.
在对称轴的左侧,y随着x的增大而增大. 在对称轴的右侧, y随着x的增大而减小.
根据图形填表:
(五)、学习回顾:
抛物线 开口方向 对称轴 顶点坐标
y=ax2(a>0)
y=ax2+k(a>0)
y=a(x-h)2(a>0)
y=a(x-h)2 +k(a>0)
y= ax2 +bx+c(a>0)
填写表格:
1.相同点:
(1)形状相同(图像都是抛物线,开口方向相同).
(2)都是轴对称图形.
(3)都有最(大或小)值.
(4)a>0时, 开口向上,
在对称轴左侧,y都随x的增大而减小,
在对称轴右侧,y都随 x的增大而增大.
a<0时,开口向下,
在对称轴左侧,y都随x的增大而增大,
在对称轴右侧,y都随 x的增大而减小 .
驶向胜利的彼岸
小结 拓展
回味无穷
二次函数y=ax2+bx+c(a≠0)与=ax 的关系
2.不同点: (1)位置不同(2)顶点不同:分别是 和(0,0).
(3)对称轴不同:分别是 和y轴.
(4)最值不同:分别是 和0.
3.联系: y=a(x-h) +k(a≠0) 的图象可以看成y=ax 的图象先沿x轴整体左(右)平移| |个单位(当 >0时,向右平移;当 <0时,向左平移),再沿对称轴整体上(下)平移| |个单位 (当 >0时向上平移;当 <0时,向下平移)得到的.
驶向胜利的彼岸
小结 拓展
回味无穷
二次函数y=ax2+bx+c(a≠0)与=ax 的关系
22.1 二次函数的图像和性质
1、已知抛物线y=ax2+bx+c
0
问题1
经过点(-1,0),则___________
经过点(0,-3),则___________
经过点(4,5),则___________
对称轴为直线x=1,则___________
当x=1时,y=0,则a+b+c=_____
a
b
2
-
=1
a-b+c=0
c=-3
16a+4b+c=5
顶点坐标是(-3,4), 则h=_____,k=______,
-3
a(x+3)2+4
4
问题2
2、已知抛物线y=a(x-h)2+k
对称轴为直线x=1,则___________
代入得y=______________
代入得y=______________
h=1
a(x-1)2+k
抛物线解析式 抛物线与x轴交点坐标
(x1,0),( x2,0)
y=2(x-1)(x-3)
y=3(x-2)(x+1)
y=-5(x+4)(x+6)
-x1
- x2
求出下表中抛物线与x轴的交点坐标,看看你有什么发现?
(1,0)(3,0)
(2,0)(-1,0)
(-4,0)(-6,0)
(x1,0),( x2,0)
y=a(x___)(x____)
(a≠0)
交点式
问题3
抛物线解析式 抛物线与x轴交点坐标
(x1,0),( x2,0)
-x1
- x2
求出下表中抛物线与x轴的交点坐标,看看你有什么发现?
(1,0)(3,0)
(2,0)(-1,0)
(-4,0)(-6,0)
(x1,0),( x2,0)
y=a(x___)(x____)
(a≠0)
交点式
问题3
y=a(x-1)(x-3)(a≠0)
y=a(x-2)(x+1)(a≠0)
y=a(x+4)(x+6)(a≠0)
已知三个点坐标三对对应值,选择一般式
已知顶点坐标或对称轴或最值,选择顶点式
已知抛物线与x轴的两交点坐标,选择交点式
二次函数常用的几种解析式
一般式 y=ax2+bx+c (a≠0)
顶点式 y=a(x-h)2+k (a≠0)
交点式 y=a(x-x1)(x-x2) (a≠0)
用待定系数法确定二次函数的解析式时,应该根据条件的特点,恰当地选用一种函数表达式。
一、设
二、代
三、解
四、还原
解:
设所求的二次函数为
解得
已知一个二次函数的图象过点(0,-3) (4,5)
(-1, 0)三点,求这个函数的解析式?
∵二次函数的图象过点(0,-3)(4,5)(-1, 0)
∴
c=-3
a-b+c=0
16a+4b+c=5
a=
b=
c=
y=ax2+bx+c
16a+4b=8
a-b=3
4a+b=2
a-b=3
-3
解:
设所求的二次函数为
解得
∴所求二次函数为
y=x2-2x-3
已知一个二次函数的图象过点(0,-3) (4,5)
(-1, 0)三点,求这个函数的解析式?
一、设
二、代
三、解
四、还原
∵二次函数的图象过点(0,-3)(4,5)(-1, 0)
∴
c=-3
a-b+c=0
16a+4b+c=5
a=
b=
c=
1
-2
-3
x=0时,y=-3;
x=4时,y=5;
x=-1时,y=0;
y=ax2+bx+c
解:
设所求的二次函数为 y=a(x-3)(x+1)
已知一个二次函数的图象过点(0, -3)
(-1,0) (3,0) 三点,求这个函数的解析式?
变式1
∴所求二次函数为 y=(x-3)(x+1)
即 y=x2-2x-3
依题意得 -3=a(0-3)(0+1)
解得 a=1
解:
设所求的二次函数为
已知抛物线的顶点为(1,-4),
且过点(0,-3),求抛物线的解析式?
点( 0,-3)在抛物线上
a-4=-3,
∴所求的抛物线解析式为 y=(x-1)2-4
变式2
∵
∴
∴ a=1
最低点为(1,-4)
x=1,y最值=-4
y=a(x-1)2-4
解:
设所求的二次函数为
已知一个二次函数的图象过点(0,-3) (4,5)
对称轴为直线x=1,求这个函数的解析式?
变式3
y=a(x-1)2+k
思考:怎样设二次函数关系式
如图,直角△ABC的两条直角边OA、OB的长分别是1和3,将△AOB绕O点按逆时针方向旋转90°,至△DOC的位置,求过C、B、A三点的二次函数解析式。
C
A
O
B
D
x
y
当抛物线上的点的坐标未知时, 应根据题目中的隐含条件求出点的坐标
(1,0)
(0,3)
(-3,0)
(1)过点(2,4),且当x=1时,y有最值为6;
(2)如图所示,
根据条件求出下列二次函数解析式:
-1
2
O
-1
数学是来源于生活又服务于生活的.
3.2米
8米
小燕去参观一个蔬菜大棚,大棚的横截面为抛物线,有关数据如图所示。小燕身高1.40米,在她不弯腰的情况下,横向活动范围是多少?
M
N
8米
3.2
A
B
A
B
C
8米
3.2
8米
3.2
A
B
O
O
O
8米
3.2
A
B
C
N
M
已知三个点坐标三对对应值,选择一般式
已知顶点坐标或对称轴或最值,选择顶点式
已知抛物线与x轴的两交点坐标,选择交点式
二次函数常用的几种解析式
一般式 y=ax2+bx+c (a≠0)
顶点式 y=a(x-h)2+k (a≠0)
交点式 y=a(x-x1)(x-x2) (a≠0)
用待定系数法确定二次函数的解析式时,应该根据条件的特点,恰当地选用一种函数表达式。
第二十二章 二次函数
……本章主要内容……
22.1 二次函数的图像和性质
22.1 二次函数的图像和性质
基础回顾 什么叫函数
在某变化过程中的两个变量x、y,当变量x在某个范围内取一个确定的值,另一个变量y总有唯一的值与它对应。
这样的两个变量之间的关系我们把它叫做函数关系。
对于上述变量x 、y,我们把y叫x的函数。 x叫自变量, y叫应变量。
目前,我们已经学习了那几种类型的函数?
二次函数
变量之间的关系
函数
一次函数
反比例函数
y=kx+b (k≠0)
正比例函数y=kx (k≠0)
y=k/x (k≠0)
节日的喷泉给人带来喜庆,你是否注意过水流所经过的路线?它会与某种函数有联系吗?
奥运赛场腾空的篮球
正方体的六个面是全等的正方形,设正方形的棱长为x,表面积为y,显然对于x的每一个值,y都有一个对应值,即y是x的函数,它们的具体关系可以表示为
问题:
y=6x2
函数①②③有什么共同点
观察:
y=6x2①
在上面的问题中,函数都是用自变量的二次式表示的。
定义:一般地,形如y=ax +bx+c(a,b,c是常数,a≠ 0)的函数叫做二次函数。其中x是自变量,a为二次项系数,ax2叫做二次项,b为一次项系数,bx叫做一次项,c为常数项。
(1)等号左边是变量y,右边是关于自变量 x的
(3 )等式的右边最高次数为 ,可以没有一次 项和常数项,但不能没有二次项。
注意:
(2)a,b,c为常数,且
(4)x的取值范围是任意实数。
整式。
a≠0.
2
(5)函数的右边是一个 整 式。
二次函数的一般形式:
y=ax2+bx+c (其中a、b、c是常数,a≠0)
二次函数的特殊形式:
当b=0时, y=ax2+c
当c=0时, y=ax2+bx
当b=0,c=0时, y=ax2
1、 说出下列二次函数的二次项系数、一次项系
数、常数项
(1) y=-x2+58x-112
(2)y=πx2
2、指出下列函数y=ax +bx+c中的a、b、c
(1) y=-3x2-x-1
(3) y=x(1+x)
(2) y=5x2-6
例1、下列函数中,哪些是二次函数?若是,分别指出二次项系数,一次项系数,常数项。
(1) y=3(x-1) +1 (2) y=x+
(3) s=3-2t (4) y=(x+3) -x
(5)y= -x (6) v=8π r
1
x
__
x
1
__
思考:2. 二次函数的一般式y=ax2+bx+c(a≠0)与一元二次方程ax2+bx+c=0(a≠0)有什么联系和区别?
驶向胜利的彼岸
联系(1)等式一边都是ax2+bx+c且 a ≠0 (2)方程ax2+bx+c=0可以看成是函数y= ax2+bx+c中y=0时得到的.
区别:前者是函数.后者是方程.等式另一边前者是y,后者是0
知识运用
例1:下列函数中,哪些是二次函数?
(1)y=3x-1 ( ) (2)y=3x2 ( )
(3)y=3x3+2x2 ( ) (4)y=2x2-2x+1( )
(5)y=x-2+x ( ) (6)y=x2-x(1+x) ( )
不是
是
不是
不是
是
不是
知识运用
m2—2m-1=2 m+1 ≠0 ∴m=3
例2:m取何值时, 函数y= (m+1)x
+(m-3)x+m 是二次函数?
解:由题意得
一次函数y=kx+b (k ≠0),其中包括正比例函数 y=kx(k≠0),
反比例函数y= (k≠0) ,
二次函数y=ax2+bx+c(a≠0)。
现在我们学习过的函数有:
可以发现,这些函数的名称都形象地反映了函数表达式与自变量的关系。
想一想
例2、y=(m+3)x
(1)m取什么值时,此函数是正比例函数?
(2) m取什么值时,此函数是反比例函数?
(3) m取什么值时,此函数是二次函数?
m2-7
解:(1)当m2-7=1且m+3≠0即m=± 时是正比例函数。
(2)当m2-7=-1且m+3≠0即m=± 时是反比例函数。
(3)当m2-7=2且m+3≠0即m=3时是二次函数。
1.一个圆柱的高等于底面半径,写出它的表面积 s 与半径 r 之间的关系式.
2. n支球队参加比赛,每两队之间进行一场比赛,写出比赛的场次数 m与球队数 n 之间的关系式.
S=2πr2 +2πr2 即S=4πr2
即
3、下列函数中,(x是自变量),是二次函数的有 。
A y=ax2+bx+c B y2=x2-4x+1
C y=x2 D y=2+ √x2+1
4.函数 y=(m-n)x2+ mx+n 是二次函数的条件是( )
A m,n是常数,且m≠0 B m,n是常数,且n≠0
C m,n是常数,且m≠n D m,n为任何实数
B C
C
一农民用40m长的篱笆围成一个一边靠墙的长方形菜园,和墙垂直的一边长为Xm,菜园的面积为Ym2,求y与x之间的函数关系式,并说出自变量的取值范围。当x=12m时,计算菜园的面积。
xm
y m2
xm
(40-2x )m
解:
由题意得:
Y=x(40-2x)
即:Y=-2x2+40x
(0
Y=-2x2+40x=-2×122+40×12
=192(m2)
多边形的对角线数d与边数n有什么关系?
问题2:
由图可以想出,如果多边形有n条边,那么它有 个顶点,从一个顶点出发,连接与这点不相邻的各顶点,可以作 条
对角线.
n
(n-3)
因为像线段MN与NM那样,连接相同两顶点的对角线是同一条对角线,所以多边形的对角线总数
M
N
即
在实践中感悟
横看成岭侧成峰,远近高低各不同
——变换角度分析问题
若函数y=x2m+n - 2xm-n+3是以x为自变量的二次函数,求m、n的值。
① ② ③ ④ ⑤
∵
2m+n=2
m-n=1
∴ m=1
n=0
∵
∴
2m+n=1
m-n=2
m=1
n=-1
∵
∴
2m+n=2
m-n=2
m=4/3
n=-2/3
∵
∴
2m+n=2
m-n=0
m=2/3
n=-4/3
∵
∴
2m+n=0
m-n=2
m=2/3
n=2/3
22.1 二次函数的图像和性质
1、一次函数的图像有何特征?
一次函数的图像是一条 。
当 时,y随x的增大而增大;
当 时,y随x的增大而减小。
2、反比例函数的图像有何特征?
反比例函数的图像是 ,共有 支,且关于 对称。
当 时,图像在 象限,在每个象限内y随x的增大而减小;
当 时,图像在 象限,在每个象限内y随x的增大而 。
直线
双曲线
两
原点
增大
一、三
二、四
k>0
k>0
k<0
k<0
3、画函数图像的基本步骤是:
、 、 。
列表
描点
连线
…二次函数的图像和性质…
y=ax2的函数图像
y=ax2 +k 的函数图像
y=a(x-h)2的函数图像
y=a(x-h)2 +k 的函数图像
y=ax2+bx+c 的函数图像
…二次函数的图像和性质…
y=ax2的函数图像
y=ax2 +k 的函数图像
y=a(x-h)2的函数图像
y=a(x-h)2 +k 的函数图像
y=ax2+bx+c 的函数图像
画形如y=ax2的函数图像:
1、画函数y=x2的图像;
观察y=x2的表达式,选择适当x值,并计算相应的y值,完成下表:
x … …
y=x2 … …
9
4
1
1
0
4
9
-3
-2
-1
0
1
2
3
x
y
0
-4
-3
-2
-1
1
2
3
4
10
8
6
4
2
-2
描点,连线
y=x2
二次函数y=x2的图象形如物体抛射时所经过的路线,我们把它叫做抛物线
二次函数 y = x2的图象是一条曲线,它的形状类似于投篮球时球在空中所经过的路线,只是这条曲线开口向上,这条曲线叫做抛物线 y = x2 ,
-3
3
3
6
9
二次函数的图象都是抛物线。
一般地,二次函数 y = ax2 + bx + c(a≠0)的图象叫做抛物线y = ax2 + bx + c
思考:这个二次函数图象有什么特征?
(1)形状是开口向上的抛物线
(2)图象关于y轴对称
(3)有最低点,没有最高点
y轴是抛物线y = x 2 的对称轴,抛物线y = x 2 与它的对称轴的交点(0,0)叫做抛物线y = x2 的顶点,它是抛物线y = x 2 的最低点.
-3
3
3
6
9
实际上,每条抛物线都有对称轴,抛物线与对称轴的交点叫做抛物线的顶点.顶点是抛物线的最低点或最高点.
思考:这个二次函数图象有什么特征?
(1)形状是开口向上的抛物线
(2)图象关于y轴对称
(3)有最低点,没有最高点
例1 在同一直角坐标系中,画出函数 的图象.
解:分别填表,再画出它们的图象,如图
x ··· -4 -3 -2 -1 0 1 2 3 4 ···
···
···
x ··· -2 -1.5 -1 -0.5 0 0.5 1 1.5 2 ···
··· ···
8
2
0.5
0
8
4.5
2
0.5
4.5
4.5
8
2
0.5
0
8
4.5
2
0.5
-2
2
2
4
6
4
-4
8
函数 的图象与函数 y=x2 的图象相比,有什么共同点和不同点?
相同点:开口都向上,顶点是原点而且是抛物线的最低点,对称轴是 y 轴
不同点:a 要越大,抛物线的开口越小.
-2
2
2
4
6
4
-4
8
你画出的图象与图中相同吗?
探究
画出函数 的图象,并考虑这些抛物线有什么共同点和不同点.
x ··· -4 -3 -2 -1 0 1 2 3 4 ···
···
···
x ··· -2 -1.5 -1 -0.5 0 0.5 1 1.5 2 ···
··· ···
-8
-4.5
-2
-0.5
0
-8
-4.5
-2
-0.5
-8
-4.5
-2
-0.5
0
-8
-4.5
-2
-0.5
-2
2
-2
-4
-6
4
-4
-8
对比抛物线,y=x2和y=-x2.它们关于x轴对称吗?一般地,抛物线y=ax2和y=-ax2呢?
一般地,抛物线 y=ax2 的对称轴是_____,顶点是______.
当a>0时,抛物线的开口______,顶点是抛物线的最______点,a越大,抛物线的开口越_______;
当a<0时,抛物线的开口_______,顶点是抛物线的最________点,a越大,抛物线的开口越_________.
向下
高
大
练习:
函数 的图象是 ,顶点坐标是 ,对称轴是 ,开口方向是 .
y轴
原点
向上
低
小
3、试说出函数y=ax2(a是常数,a≠0)的图象的开口方向、对称轴和顶点坐标,并填写下表.
y=ax2
向上
向下
y轴
y轴
(0,0)
(0,0)
|a|越大开口越小, |a|越小开口越大。
反馈测试
抛物线y=4x2中的开口方向是 ,顶点坐标是 ,对称轴是 .
抛物线 y= -
x2 的开口方向是 ,顶点坐标是 , 对称轴是 .
3. 二次函数y=ax2与y=2x2,开口大小,形状一样,开口方向相反,则a= .
…二次函数的图像和性质…
y=ax2的函数图像
y=ax2 +k 的函数图像
y=a(x-h)2的函数图像
y=a(x-h)2 +k 的函数图像
y=ax2+bx+c 的函数图像
1.二次函数y=2x2的图象是____,它的开口向_____,顶点坐标是_____;对称轴是______,在对称轴的左侧,y随x的增大而______,在对称轴的右侧,y随x的增大而______,函数y=2x2当x=______时, y有最______值,其最______值是______。
课前复习
2、二次函数 y=2x 、 的图象与二次函数 y=x 的图象有什么相同和不同?
a>0
O
x
y
1
2
3
4
5
1
2
3
4
5
–5
–4
–3
–2
–1
–5
–4
–3
–2
–1
a<0
3、试说出函数y=ax2(a是常数,a≠0)的图象的开口方向、对称轴和顶点坐标,并填写下表.
y=ax2
向上
向下
y轴
y轴
(0,0)
(0,0)
4、二次函数y=2x2+1的图象与二次函数y=2x2的图象开口方向、对称轴和顶点坐标是否相同 它们有什么关系?我们应该采取什么方法来研究这个问题?
画出函数y=2x2和函数y= 2x2+1的图象,并加以比较
(1)二次函数 y=2x +1 的图象与二次函数 y=2x 的图象有什么关系?
x … –1.5 –1 –0.5 0 0.5 1 1.5 …
y=2x2 … 4.5 2 0.5 0 0.5 2 4.5 …
y=2x2+1 … 5.5 3 1.5 1 1.5 3 5.5 …
(0,1)
x … –1.5 –1 –0.5 0 0.5 1 1.5 …
y=2x2 … 4.5 2 0.5 0 0.5 2 4.5 …
y=2x2+1 … 5.5 3 1.5 1 1.5 3 5.5 …
(0,1)
问题1:当自变量x取同一数值时,这两个函数的函数值之间有什么关系 反映在图象上,相应的两个点之间的位置又有什么关系
2、函数y=2x2+1的图象可以看成是将函数y=2x2的图象向上平移一个单位得到的。
1、函数y=2x2+1与y=2x2的图象开口方向、对称轴相同,但顶点坐标不同,函数y= 2x2的图象的顶点坐标是(0,0),而函数y=2x2+1的图象的顶点坐标是(0,1)。
函数y=2x2+1和y=2x2的图象有什么联系
你能由函数y=2x2的性质,得到函数y=2x2+1的一些性质吗
完成填空:
当x______时,函数值y随x的增大而减小;当x______时,函数值y随x的增大而增大,当x______时,函数取得最______值,最______值y=______.
以上就是函数y=2x2+1的性质。
﹥0
﹤0
=0
小
小
1
(2)二次函数 y=3x -1 的图象与二次函数 y=3x 的图象有什么关系?
x … –1 –0.6 –0.3 0 0.3 0.6 1 …
y=3x2 … 3 1.08 0.27 0 0.27 1.08 3 …
y=3x2–1 … 2 0.08 –0.73 – 1 –0.73 0.08 2 …
(0,-1)
a>0
(3)在同一直角坐标系中画出函数
的图像
O
x
y
1
2
3
4
5
1
2
3
4
5
–5
–4
–3
–2
–1
–5
–4
–3
–2
–1
y
在同一直角坐标系中画出函数
的图像
a<0
(0,2)
(0,-2)
试说出函数y=ax2+k(a、k是常数,a≠0)的图象的开口方向、对称轴和顶点坐标,并填写下表.
向上
向下
y轴
y轴
(0,k)
(0,k)
|a|越大开口越小,反之开口越大。
练习
1.把抛物线 向下平移2个单位,可以得到抛物线 ,再向上平移5个单位,可以得到抛物线 ;
2.对于函数y= –x2+1,当x 时,函数值y随x的增大而增大;当x 时,函数值y随x的增大而减小;当x 时,函数取得最 值,为 。
<0
>0
=0
大
0
3.函数y=3x2+5与y=3x2的图象的不同之处是( )
A.对称轴 B.开口方向 C.顶点 D.形状
4.已知抛物线y=2x2–1上有两点(x1,y1 ) ,(x2,y2 )且x1<x2<0,则y1 y2(填“<”或“>”)
5.已知抛物线 ,把它向下平移,得到的抛物线与x轴交于A、B两点,与y轴交于C点,若⊿ABC是直角三角形,那么原抛物线应向下平移几个单位?
C
…二次函数的图像和性质…
y=ax2的函数图像
y=ax2 +k 的函数图像
y=a(x-h)2的函数图像
y=a(x-h)2 +k 的函数图像
y=ax2+bx+c 的函数图像
y=ax2+k a>0 a<0
图象
开口
对称性
顶点
增减性
二次函数y=ax2+k的性质
开口向上
开口向下
a的绝对值越大,开口越小
关于y轴对称
顶点是最低点
顶点是最高点
在对称轴左侧递减
在对称轴右侧递增
在对称轴左侧递增
在对称轴右侧递减
k>0
k<0
k<0
k>0
(0,k)
x … -3 -2 -1 0 1 2 3 …
解:列表
画出二次函数 、 的图像,并考虑它们的开口方向、对称轴和顶点.
-2
…
0
-0.5
-2
-0.5
-8
…
-4.5
-8
…
-2
-0.5
0
-4.5
-2
…
-0.5
1
2
3
4
5
x
-1
-2
-3
-4
-5
-6
-7
-8
-9
1
y
o
-1
-2
-3
-4
-5
-10
x=-1
抛物线 与 的开口方向、对称轴、顶点
抛物线 与
抛物线
有什么关系
1
2
3
4
5
x
-1
-2
-3
-4
-5
-6
-7
-8
-9
1
y
o
-1
-2
-3
-4
-5
-10
1
2
3
4
5
x
-1
-2
-3
-4
-5
-6
-7
-8
-9
1
y
o
-1
-2
-3
-4
-5
-10
向左平移1个单位
向右平移1个单位
在同一坐标系中作出下列二次函数:
观察三条抛物线的相互关系,并分别指出它们的开口方向,对称轴及顶点.
顶点(0,0)
顶点(2,0)
直线x=-2
直线x=2
向右平移2个单位
向左平移2个单位
顶点(-2,0)
对称轴:y轴
即直线: x=0
在同一坐标系中作出下列二次函数:
观察三条抛物线的相互关系,并分别指出它们的开口方向,对称轴及顶点.
向右平移2个单位
向右平移2个单位
向左平移2个单位
向左平移2个单位
一般地,抛物线y=a(x-h)2有如下特点:
(1)对称轴是x=h;
(2)顶点是(h,0).
(3)抛物线y=a(x-h)2可以由抛物线y=ax2向左或向右平移|h|得到.
h>0,向右平移;h<0,向左平移
x
y
y=a(x-h)2 a>0 a<0
图象
开口
对称性
顶点
增减性
二次函数y=a(x-h)2的性质
开口向上
开口向下
a的绝对值越大,开口越小
直线x=h
顶点是最低点
顶点是最高点
在对称轴左侧递减
在对称轴右侧递增
在对称轴左侧递增
在对称轴右侧递减
h>0
h<0
h<0
h>0
(h,0)
y=-2(x+3)2
1、说出抛物线的开口方向、对称轴、顶点,最大值或最小值各是什么及增减性如何?
y=2(x-3)2
y=-2(x-2)2
y=3(x+1)2
2、若将抛物线y=-2(x-2)2的图象的顶点移到原点,则下列平移方法正确的是( )
A、向上平移2个单位
B、向下平移2个单位
C、向左平移2个单位
D、向右平移2个单位
C
3、抛物线y=4(x-3)2的开口方向 ,对称轴是 ,顶点坐标是 ,抛物线是最 点,
当x= 时,y有最 值,其值为 。
抛物线与x轴交点坐标 ,与y轴交点坐标 。
向上
直线x=3
(3,0)
低
3
小
0
(3,0)
(0,36)
4.用配方法把下列函数化成y=a(x-h)2的形式,并说出开口方向,顶点坐标和对称轴。
5、按下列要求求出二次函数的解析式:
(1)已知抛物线y=a(x-h)2经过点
(-3,2)(-1,0)求该抛物线线的解析式。
(2)形状与y=-2(x+3)2的图象形状相同,但开口方向不同,顶点坐标是(1,0)的抛物线解析式。
(3)已知二次函数图像的顶点在x轴上,且图像经过点(2,-2)与(-1,-8)。求此函数解析式。
抛物线 开口方向 对称轴 顶点坐标
y = 2(x+3)2
y = -3(x-1)2
y = -4(x-3)2
向上
直线x=-3
( -3 , 0 )
直线x=1
直线x=3
向下
向下
( 1 , 0 )
( 3, 0)
3.抛物线y=ax2+k有如下特点:
当a>0时, 开口向上;
当a<0时,开口向上.
(2)对称轴是y轴;
(3)顶点是(0,k).
抛物线y=a(x-h)2有如下特点:
(1)当a>0时, 开口向上,当a<0时,开口向上;
(2)对称轴是x=h;
(3)顶点是(h,0).
2.抛物线y=ax2+k可以由抛物线y=ax2向上或向下平移|k|得到.
抛物线y=a(x-h)2可以由抛物线y=ax2向左或向右平移|h|得到.
(k>0,向上平移;k<0向下平移.)
(h>0,向右平移;h<0向左平移.)
1.抛物线y=ax2+k、抛物线y=a(x-h)2和抛物线y=ax2的形状完全相同,开口方向一致;
(1)当a>0时, 开口向上,当a<0时,开口向下;
如何平移:
…二次函数的图像和性质…
y=ax2的函数图像
y=ax2 +k 的函数图像
y=a(x-h)2的函数图像
y=a(x-h)2 +k 的函数图像
y=ax2+bx+c 的函数图像
在同一坐标系中作出二次函数y=3x2和y=3(x-1)2的图象.观察图象,回答问题
(1)函数y=3(x-1)2的图象与y=3x2的图象有什么关系 它是轴对称图形吗 它的对称轴和顶点坐标分别是什么
(2)x取哪些值时,函数y=3(x-1)2的值随x值的增大而增大 x取哪些值时,函数y=3(x-1)2的值随x的增大而减少?
在同一坐标系中,作出二次函数y=3x , y=3(x-1)2和y=3(x-1)2+2的图象.
根据图象回答问题:三个图象有什么关系 它们的开口方向,对称轴和顶点坐标分别是什么
对称轴仍是平行于y轴
的直线x=1;增减性与
y=3x2类似.
顶点是(1,2).
二次函数y=3(x-1)2+2的
图象可以看作是抛物线
y=3x2先沿着x轴向右平移
1个单位,再沿直线x=1向
上平移2个单位后得到的.
开口向上,当
X=1时有最小
值:且最小值=2.
先猜一猜,再做一做,在同一坐标系中作二次函数y=3(x-1)2-2,会是什么样
X=1
对称轴仍是平行于y轴的直线
(x=1);增减性与y=3x2类似.
顶点是(1,-2)
二次函数y=3(x-1)2-2的
图象可以看作是抛物线
y=3x2先沿着x轴向右平移
1个单位,再沿直线x=1向
下平移2个单位后得到的.
二次函数y=3(x-1)2-2的图象与抛物线y=3x2和y=3(x-1)2有何关系 它的开口方向、对称轴和顶点坐标分别是什么
开口向上,
当x=1时y有
最小值:且
最小值= -2.
二次函数y=-3(x-1)2+2和y=-3(x-1)2, y=-3x 的图象有什么关系 它们的开口方向,对称轴和顶点坐标分别是什么 再作图看一看.
X=1
在同一坐标系中,作出二次函数y=-3(x-1)2+2, y=-3(x-1)2-2, y=-3x 和
y=-3(x-1)2的图象。
根据图像
回答问题
对称轴仍是平行于y轴的直线
(x=1);增减性与y=-3x2类似.
顶点分别是
(1,2)和(1,-2).
二次函数
y=-3(x-1)2+2与y=-3(x-1)2+2的
图象可以看作是抛物线y=-3x2先沿
着x轴向右平移1个单位,再沿直线
x=1向上(或向下)平移2个单位后
得到的.
二次函数y=-3(x-1)2+2与y=-3(x-1)2-2的图象和抛物线y=-3x ,y=-3(x-1)2有什么关系 它的开口方向,对称轴和顶点坐标分别是什么
开口向下,当x=1
时y有最大值;且
最大值=2(或
最大值=-2).
想一想,二次函数y=-3(x+1)2+2与y=-3(x+1)2-2的图象和抛物线y=-3x ,y=-3(x+1)2
y
X=1
对称轴仍是平行于y轴的直线
(x=-1);增减性与y= -3x2类似.
顶点分别是
(-1,2)和(-1,-2)..
二次函数y=-3(x+1)2+2与
y=-3(x+1)2-2的图象可
以看作是抛物线y=-3x2
先沿着x轴向左平移1个
单位,再沿直线x=-1向上
(或向下)平移2个单位后
得到的.
二次函数y=-3(x+1)2+2与y=-3(x+1)2-2的图象和抛物线y=-3x ,y=-3(x+1)2有什么关系 它的开口方向,对称轴和顶点坐标分别是什么
开口向下,
当x=-1时y有
最大值:且
最大值= 2
(或最大值= - 2).
先想一想,再总结二次函数y=a(x-h)2+k的图象和性质.
x=1
一般地,由y=ax 的图象便可得到二次函数y=a(x-h) +k的图象:y=a(x-h) +k(a≠0) 的图象可以看成y=ax 的图象先沿x轴整体左(右)平移|h|个单位(当h>0时,向右平移;当h<0时,向左平移),再沿对称轴整体上(下)平移|k|个单位 (当k>0时,向上平移;当k<0时,向下平移)得到的.
因此,二次函数y=a(x-h) +k的图象是一条抛物线,它的开口方向、对称轴和顶点坐标与a,h,k的值有关.
归纳
用平移观点看函数:
抛物线 与抛物线 形状相同,位置不同.
二次函数 特点:
归纳
1.图象是一条抛物线,对称轴为直线
x=h,顶点为(h,k)。
2.当a>0时,开口向上;
当x=h时,y取最小值为k;
在对称轴的左侧,y随x的增大而减小,
在对称轴的右侧,y随x的增大而增大.
3.当a<0时,开口向下;
当x=h时,y取最大值为k;
在对称轴的左侧,y随x的增大而增大,
在对称轴的右侧,y随x的增大而减小.
二次函数y=a(x-h)2+k的图象和性质
1.顶点坐标与对称轴
2.位置与开口方向
3.增减性与最值
抛物线
顶点坐标
对称轴
位置
开口方向
增减性
最值
y=a(x-h)2+k(a>0)
y=a(x-h)2+k(a<0)
(h,k)
(h,k)
直线x=h
直线x=h
由h和k的符号确定
由h和k的符号确定
向上
向下
当x=h时,最小值为k.
当x=h时,最大值为k.
在对称轴的左侧,y随着x的增大而减小. 在对称轴的右侧, y随着x的增大而增大.
在对称轴的左侧,y随着x的增大而增大. 在对称轴的右侧, y随着x的增大而减小.
根据图形填表:
1.指出下列函数图象的开口方向对称轴和顶点坐标及最值:
3.对于二次函数y=3(x+1)2,当x取哪些值时,y的值随x值的增大而增大 当x取哪些值时,y的值随x值的增大而减小 二次函数y=3(x+1)2+4呢
2.(1)二次函数y=3(x+1)2的图象与二次函数y=3x2的图象有什么关系 它是轴对称图形吗 它的对称轴和顶点坐标分别是什么
(2)二次函数 y=-3(x-2)2+4 的图象与二次函数 y=-3x2的图象有什么关系
2.不同点: 只是位置不同(1)顶点不同:分别是(h,k)和(0,0).
(2)对称轴不同:分别是直线x= h和y轴.
(3)最值不同:分别是k和0.
3.联系: y=a(x-h) +k(a≠0) 的图象可以看成y=ax 的图象先沿x轴整体左(右)平移|h|个单位(当h>0时,向右平移;当h<0时,向左平移),再沿对称轴整体上(下)平移|k|个单位 (当k>0时向上平移;当k<0时,向下平移)得到的.
1.相同点: (1)形状相同(图像都是抛物线,开口方向相同).
(2)都是轴对称图形.
(3)都有最(大或小)值.
(4)a>0时, 开口向上,在对称轴左侧,y都随x的增大而减小,在对称轴右侧,y都随 x的增大而增大. a<0时,开口向下,在对称轴左侧,y都随x的增大而增大,在对称轴右侧,y都随 x的增大而减小 .
二次函数y=a(x-h) +k与y=ax 的关系
1.指出下列函数图象的开口方向,对称轴和顶点坐标.必要时作出草图进行验证.
2.填写下表:
y=a(x-h) +k 开口方向 对称轴 顶点坐标
a>0
a<0
…二次函数的图像和性质…
y=ax2的函数图像
y=ax2 +k 的函数图像
y=a(x-h)2的函数图像
y=a(x-h)2 +k 的函数图像
y=ax2+bx+c 的函数图像
一般地,抛物线y=a(x-h) +k与y=ax 的 相同, 不同
2
2
形状
位置
y=ax
2
y=a(x-h) +k
2
上加下减
左加右减
抛物线y=a(x-h)2+k有如下特点:
1.当a﹥0时,开口 ,
当a﹤0时,开口 ,
向上
向下
2.对称轴是 ;
3.顶点坐标是 。
直线X=h
(h,k)
二次函数 开口方向 对称轴 顶点坐标
y=2(x+3)2+5
y = -3x(x-1)2 -2
y = 4(x-3)2 +7
y = -5(2-x)2 - 6
直线x=–3
直线x=1
直线x=2
直线x=3
向上
向上
向下
向下
(-3,5)
(1,-2)
(3,7 )
(2,-6)
你能说出二次函数y=—x -6x+21图像的特征吗?
2
1
2
探究:
如何画出 的图象呢
我们知道,像y=a(x-h)2+k这样的函数,容易确定相应抛物线的顶点为(h,k), 二次函数 也能化成这样的形式吗
配方
y= — (x―6) +3
2
1
2
你知道是怎样配方的吗?
(1)“提”:提出二次项系数;
( 2 )“配”:括号内配成完全平方;
(3)“化”:化成顶点式。
归纳
二次函数 y= —x -6x +21图象的
画法:
(1)“化” :化成顶点式 ;
(2)“定”:确定开口方向、对称轴、顶
点坐标;
(3)“画”:列表、描点、连线。
2
1
2
5
10
5
10
O
x
y
x … 3 4 5 6 7 8 9 …
… 7.5 5 3.5 3 3.5 5 7.5 …
求次函数y=ax +bx+c的对称轴和顶点坐标.
函数y=ax +bx+c的顶点是
配方:
提取二次项系数
配方:加上再减去一次项系数绝对值一半的平方
整理:前三项化为平方形式,后两项合并同类项
化简:去掉中括号
这个结果通常称为求顶点坐标公式.
函数y=ax +bx+c的对称轴、顶点坐标是什么?
1. 说出下列函数的开口方向、对称轴、顶点坐标:
函数y=ax +bx+c的对称轴、顶点坐标是什么?
例1:指出抛物线:
的开口方向,求出它的对称轴、顶点坐标、与y轴的交点坐标、与x轴的交点坐标。并画出草图。
对于y=ax2+bx+c我们可以确定它的开口方向,求出它的对称轴、顶点坐标、与y轴的交点坐标、与x轴的交点坐标(有交点时),这样就可以画出它的大致图象。
方法归纳
配方法
1
公式法
2
单击添加文字内容
3
①y=2x2-5x+3
③y=(x-3)(x+2)
②y=- x2+4x-9
求下列二次函数图像的开口、顶点、对称轴
请画出草图:
3
-9
-6
抛物线位置与系数a,b,c的关系:
⑴a决定抛物线的开口方向:
a>0 开口向上
a<0 开口向下
⑵ a,b决定抛物线对称轴的位置:
(对称轴是直线x = -— )
① a,b同号<=> 对称轴在y轴左侧;
② b=0 <=> 对称轴是y轴;
③ a,b异号<=> 对称轴在y轴右侧
2a
b
【左同右异】
⑶ c决定抛物线与y轴交点的位置:
① c>0 <=>图象与y轴交点在x轴上方;
② c=0 <=>图象过原点;
③ c<0 <=>图象与y轴交点在x轴下方。
⑷顶点坐标是( , )。
(5)二次函数有最大或最小值由a决定。
当x=- — 时,y有最大(最小)值 y=
b
2a
______________________
4a
4ac-b
2
-1
例2、已知函数y = ax2 +bx +c的图象如下图所示,x= 为该图象的对称轴,根
据图象信息你能得到关于系数a,b,c的一些什么结论?
y
1
.
.
x
1
3
1.抛物线y=2x2+8x-11的顶点在 ( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
2.不论k 取任何实数,抛物线y=a(x+k)2+k(a≠0)的顶点都在 ( )
A.直线y = x上 B.直线y = - x上
C.x轴上 D.y轴上
3.若二次函数y=ax2 + 4x+a-1的最小值是2,则a的值是 ( )
A 4 B. -1 C. 3 D.4或-1
C
B
A
4.若二次函数 y=ax2 + b x + c 的图象如下,与x轴的一个交点为(1,0),则下列各式中不成立的是 ( )
A.b2-4ac>0 B. <0
C.a+b+c=0 D. >0
1
x
y
o
-1
5.若把抛物线y = x2 - 2x+1向右平移2个单位,再向下平移3个单位,得抛物线y=x2+bx+c,则( )
A.b=2 c= 6 B.b=-6 , c=6
C.b=-8 c= 6 D.b=-8 , c=18
B
B
-
2a
b
4a
4ac-b2
6.若一次函数 y=ax+b 的图象经过第二、三、四象限,则二次函数 y=ax2+bx-3 的大致图象是 ( )
7.在同一直角坐标系中,二次函数 y=ax2+bx+c 与一次函数y=ax+c的大致图象可能是 ( )
x
y
o
x
y
o
x
y
o
x
y
o
A
B
C
D
-3
-3
-3
-3
x
y
o
x
y
o
x
y
o
x
y
o
A
B
C
D
C
C
二次函数y=ax2+bx+c(a≠0)的图象和性质
1.顶点坐标与对称轴
2.位置与开口方向
3.增减性与最值
抛物线
顶点坐标
对称轴
位置
开口方向
增减性
最值
y=ax2+bx+c(a>0)
y=ax2+bx+c(a<0)
由a,b和c的符号确定
由a,b和c的符号确定
向上
向下
在对称轴的左侧,y随着x的增大而减小. 在对称轴的右侧, y随着x的增大而增大.
在对称轴的左侧,y随着x的增大而增大. 在对称轴的右侧, y随着x的增大而减小.
根据图形填表:
(五)、学习回顾:
抛物线 开口方向 对称轴 顶点坐标
y=ax2(a>0)
y=ax2+k(a>0)
y=a(x-h)2(a>0)
y=a(x-h)2 +k(a>0)
y= ax2 +bx+c(a>0)
填写表格:
1.相同点:
(1)形状相同(图像都是抛物线,开口方向相同).
(2)都是轴对称图形.
(3)都有最(大或小)值.
(4)a>0时, 开口向上,
在对称轴左侧,y都随x的增大而减小,
在对称轴右侧,y都随 x的增大而增大.
a<0时,开口向下,
在对称轴左侧,y都随x的增大而增大,
在对称轴右侧,y都随 x的增大而减小 .
驶向胜利的彼岸
小结 拓展
回味无穷
二次函数y=ax2+bx+c(a≠0)与=ax 的关系
2.不同点: (1)位置不同(2)顶点不同:分别是 和(0,0).
(3)对称轴不同:分别是 和y轴.
(4)最值不同:分别是 和0.
3.联系: y=a(x-h) +k(a≠0) 的图象可以看成y=ax 的图象先沿x轴整体左(右)平移| |个单位(当 >0时,向右平移;当 <0时,向左平移),再沿对称轴整体上(下)平移| |个单位 (当 >0时向上平移;当 <0时,向下平移)得到的.
驶向胜利的彼岸
小结 拓展
回味无穷
二次函数y=ax2+bx+c(a≠0)与=ax 的关系
22.1 二次函数的图像和性质
1、已知抛物线y=ax2+bx+c
0
问题1
经过点(-1,0),则___________
经过点(0,-3),则___________
经过点(4,5),则___________
对称轴为直线x=1,则___________
当x=1时,y=0,则a+b+c=_____
a
b
2
-
=1
a-b+c=0
c=-3
16a+4b+c=5
顶点坐标是(-3,4), 则h=_____,k=______,
-3
a(x+3)2+4
4
问题2
2、已知抛物线y=a(x-h)2+k
对称轴为直线x=1,则___________
代入得y=______________
代入得y=______________
h=1
a(x-1)2+k
抛物线解析式 抛物线与x轴交点坐标
(x1,0),( x2,0)
y=2(x-1)(x-3)
y=3(x-2)(x+1)
y=-5(x+4)(x+6)
-x1
- x2
求出下表中抛物线与x轴的交点坐标,看看你有什么发现?
(1,0)(3,0)
(2,0)(-1,0)
(-4,0)(-6,0)
(x1,0),( x2,0)
y=a(x___)(x____)
(a≠0)
交点式
问题3
抛物线解析式 抛物线与x轴交点坐标
(x1,0),( x2,0)
-x1
- x2
求出下表中抛物线与x轴的交点坐标,看看你有什么发现?
(1,0)(3,0)
(2,0)(-1,0)
(-4,0)(-6,0)
(x1,0),( x2,0)
y=a(x___)(x____)
(a≠0)
交点式
问题3
y=a(x-1)(x-3)(a≠0)
y=a(x-2)(x+1)(a≠0)
y=a(x+4)(x+6)(a≠0)
已知三个点坐标三对对应值,选择一般式
已知顶点坐标或对称轴或最值,选择顶点式
已知抛物线与x轴的两交点坐标,选择交点式
二次函数常用的几种解析式
一般式 y=ax2+bx+c (a≠0)
顶点式 y=a(x-h)2+k (a≠0)
交点式 y=a(x-x1)(x-x2) (a≠0)
用待定系数法确定二次函数的解析式时,应该根据条件的特点,恰当地选用一种函数表达式。
一、设
二、代
三、解
四、还原
解:
设所求的二次函数为
解得
已知一个二次函数的图象过点(0,-3) (4,5)
(-1, 0)三点,求这个函数的解析式?
∵二次函数的图象过点(0,-3)(4,5)(-1, 0)
∴
c=-3
a-b+c=0
16a+4b+c=5
a=
b=
c=
y=ax2+bx+c
16a+4b=8
a-b=3
4a+b=2
a-b=3
-3
解:
设所求的二次函数为
解得
∴所求二次函数为
y=x2-2x-3
已知一个二次函数的图象过点(0,-3) (4,5)
(-1, 0)三点,求这个函数的解析式?
一、设
二、代
三、解
四、还原
∵二次函数的图象过点(0,-3)(4,5)(-1, 0)
∴
c=-3
a-b+c=0
16a+4b+c=5
a=
b=
c=
1
-2
-3
x=0时,y=-3;
x=4时,y=5;
x=-1时,y=0;
y=ax2+bx+c
解:
设所求的二次函数为 y=a(x-3)(x+1)
已知一个二次函数的图象过点(0, -3)
(-1,0) (3,0) 三点,求这个函数的解析式?
变式1
∴所求二次函数为 y=(x-3)(x+1)
即 y=x2-2x-3
依题意得 -3=a(0-3)(0+1)
解得 a=1
解:
设所求的二次函数为
已知抛物线的顶点为(1,-4),
且过点(0,-3),求抛物线的解析式?
点( 0,-3)在抛物线上
a-4=-3,
∴所求的抛物线解析式为 y=(x-1)2-4
变式2
∵
∴
∴ a=1
最低点为(1,-4)
x=1,y最值=-4
y=a(x-1)2-4
解:
设所求的二次函数为
已知一个二次函数的图象过点(0,-3) (4,5)
对称轴为直线x=1,求这个函数的解析式?
变式3
y=a(x-1)2+k
思考:怎样设二次函数关系式
如图,直角△ABC的两条直角边OA、OB的长分别是1和3,将△AOB绕O点按逆时针方向旋转90°,至△DOC的位置,求过C、B、A三点的二次函数解析式。
C
A
O
B
D
x
y
当抛物线上的点的坐标未知时, 应根据题目中的隐含条件求出点的坐标
(1,0)
(0,3)
(-3,0)
(1)过点(2,4),且当x=1时,y有最值为6;
(2)如图所示,
根据条件求出下列二次函数解析式:
-1
2
O
-1
数学是来源于生活又服务于生活的.
3.2米
8米
小燕去参观一个蔬菜大棚,大棚的横截面为抛物线,有关数据如图所示。小燕身高1.40米,在她不弯腰的情况下,横向活动范围是多少?
M
N
8米
3.2
A
B
A
B
C
8米
3.2
8米
3.2
A
B
O
O
O
8米
3.2
A
B
C
N
M
已知三个点坐标三对对应值,选择一般式
已知顶点坐标或对称轴或最值,选择顶点式
已知抛物线与x轴的两交点坐标,选择交点式
二次函数常用的几种解析式
一般式 y=ax2+bx+c (a≠0)
顶点式 y=a(x-h)2+k (a≠0)
交点式 y=a(x-x1)(x-x2) (a≠0)
用待定系数法确定二次函数的解析式时,应该根据条件的特点,恰当地选用一种函数表达式。
同课章节目录
