人教版数学八年级上册 11.1.1 三角形的边教案
文档属性
| 名称 | 人教版数学八年级上册 11.1.1 三角形的边教案 |  | |
| 格式 | docx | ||
| 文件大小 | 388.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-18 15:19:55 | ||
图片预览


文档简介
第十一章 三角形
11.1 与三角形有关的线段
11.1.1 三角形的边
第1课时 三角形的边
一、教学目标
【知识与技能】
1.进一步认识三角形的概念及其基本要素;
2.学会对三角形进行分类;
3.理解并掌握三角形三条边之间的关系。
【过程与方法】
经历度量三角形边长的实践活动,理解三角形三边不等的关系。
【情感态度与价值观】
帮助学生树立几何知识源于客观实际,用客观实际的观念,激发学生学习的兴趣。
二、课型
新授课
三、课时
第1课时
四、教学重难点
【教学重点】
理解三角形定义、证明三角形三边关系。
【教学难点】
1.在具体的图形中不重复,且不遗漏地识别所有三角形.
2.用三角形三边不等关系判定三条线段可否组成三角形.
五、课前准备
教师:课件、三角尺、屋顶架结构图等。
学生:三角尺、铅垂纸、小刀。
六、教学过程
(一)导入新课(出示课件2)
1. 你能从中找出4个不同的三角形吗?与同学交流各自找出的三角形.
2. 这些三角形有什么共同特点?
(二)探索新知
1.观察三角形的构成,探索三角形的概念(出示课件4)
教师问1:你能画出一个三角形吗?
让学生画出三角形,直观感受三角形的构成.
教师问2:结合你画的三角形,说明三角形是由什么组成的?
学生回答:三角形是由三条线段组成的.
教师问3:什么叫三角形?
学生回答:由三条线段组成的图形叫做三角形.
教师问4:如下图,是由三条线组成的图形,这样的图形是三角形吗?
学生回答:这样的不是三角形.
教师问5:你们讨论一下,如何给三角形下定义呢?
学生讨论回答:
需要满足以下条件:
三角形的特征有:
(1)三条线段;(2)不在同一直线上;(3)首尾顺次连接.
教师画出图形:如图所示:
教师归纳:由不在同一直线上的三条线段首尾顺次相接所组成的图形叫做三角形.(出示课件5)
2.自主学习三角形的表示方法及分类
阅读教材第2页到第3页探究前内容,回答下列问题.
教师问6:根据右图回答以下问题:
(1)在三角形中,什么叫边?什么叫内角?什么叫顶点?
学生回答:
如图:线段AB、BC、CA是△ABC的三边;
点A、B、C△ABC的三个顶点;
∠A、∠B、∠C是△ABC的三个内角.
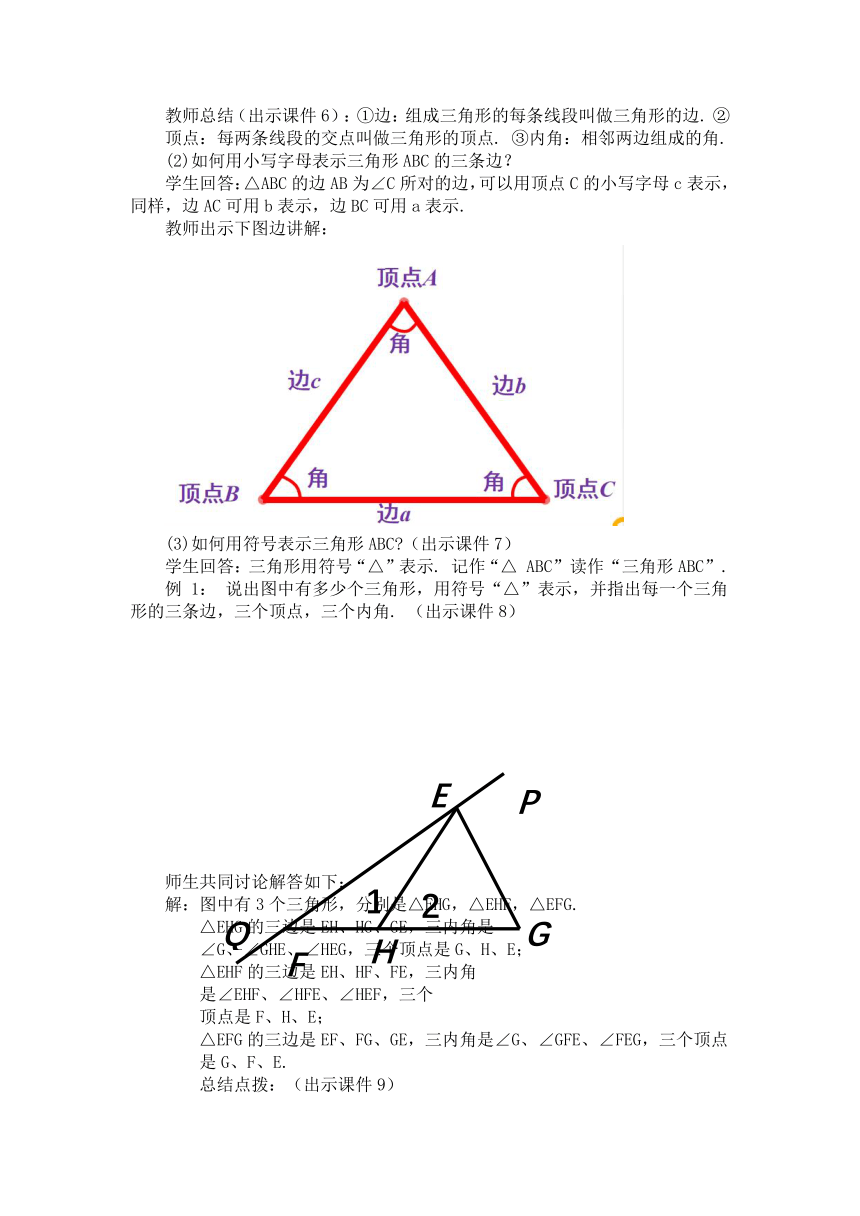
教师总结(出示课件6):①边:组成三角形的每条线段叫做三角形的边. ②顶点:每两条线段的交点叫做三角形的顶点. ③内角:相邻两边组成的角.
(2)如何用小写字母表示三角形ABC的三条边?
学生回答:△ABC的边AB为∠C所对的边,可以用顶点C的小写字母c表示,同样,边AC可用b表示,边BC可用a表示.
教师出示下图边讲解:
(3)如何用符号表示三角形ABC (出示课件7)
学生回答:三角形用符号“△”表示. 记作“△ ABC”读作“三角形ABC”.
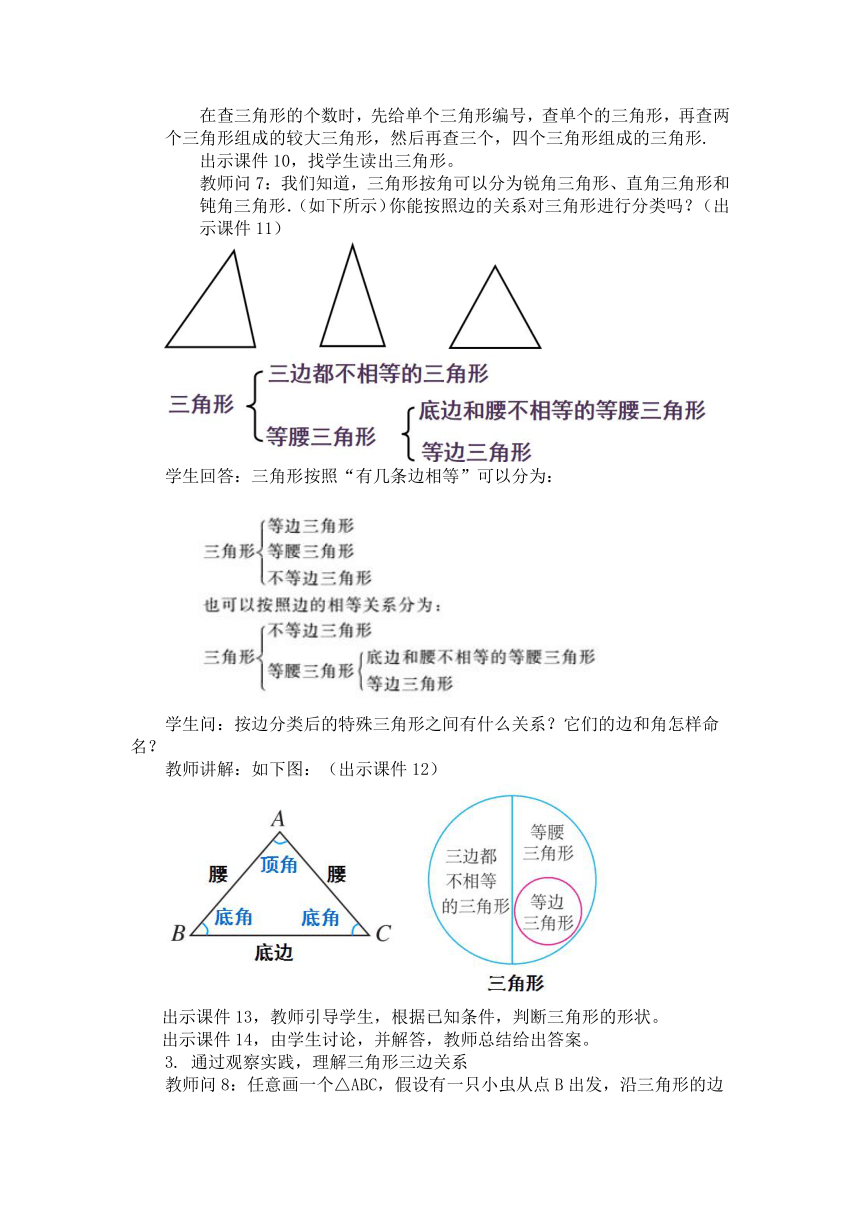
例 1: 说出图中有多少个三角形,用符号“△”表示,并指出每一个三角形的三条边,三个顶点,三个内角. (出示课件8)
师生共同讨论解答如下:
解:图中有3个三角形,分别是△EHG,△EHF,△EFG.
△EHG的三边是EH、HG、GE,三内角是
∠G、∠GHE、∠HEG,三个顶点是G、H、E;
△EHF的三边是EH、HF、FE,三内角
是∠EHF、∠HFE、∠HEF,三个
顶点是F、H、E;
△EFG的三边是EF、FG、GE,三内角是∠G、∠GFE、∠FEG,三个顶点是G、F、E.
总结点拨:(出示课件9)
在查三角形的个数时,先给单个三角形编号,查单个的三角形,再查两个三角形组成的较大三角形,然后再查三个,四个三角形组成的三角形.
出示课件10,找学生读出三角形。
教师问7:我们知道,三角形按角可以分为锐角三角形、直角三角形和钝角三角形.(如下所示)你能按照边的关系对三角形进行分类吗?(出示课件11)
学生回答:三角形按照“有几条边相等”可以分为:
学生问:按边分类后的特殊三角形之间有什么关系?它们的边和角怎样命名?
教师讲解:如下图:(出示课件12)
出示课件13,教师引导学生,根据已知条件,判断三角形的形状。
出示课件14,由学生讨论,并解答,教师总结给出答案。
3. 通过观察实践,理解三角形三边关系
教师问8:任意画一个△ABC,假设有一只小虫从点B出发,沿三角形的边爬到点C,它有几条线路可以选择?各条线路的长一样吗?
学生回答:小虫从点B出发沿三角形的边爬到点C有2条线路:(1)从B→C,即线段BC的长;(2)从B→A→C,即线段BA与线段AC长之和:BA+AC.
经过测量可得BA+AC>BC,所以这两条线路的长不一样.
根据“两点的所有连线中,线段最短”,说明BA+AC>BC.
教师讲解:由不等式的基本性质可得:AB>BC–AC.
教师问9:在A点的小狗,为了尽快吃到B点的香肠,它会选择哪条路线 如果小狗在C点呢?(出示课件15)
学生回答:从A→B,即线段AB的长;
教师问10:为什么呢?
学生回答:两点的所有连线中,线段最短.
教师问11:联系三角形的三边,从问题中你可以得到怎样的结论?(出示课件16)
学生回答:三角形两边的和大于第三边.
(出示课件17)
学生回答:三角形两边的差小于第三边.
(出示课件18-19,学生进行练习)
教师总结:三角形的三边有这样的关系:
(1) 三角形两边的和大于第三边.
(2) 三角形两边的差小于第三边.
例2 下列长度的各组线段能否组成一个三角形?(出示课件20)
(1)15cm、10cm、7cm (2) 4cm、5cm、10cm
(3) 3cm、8cm、5cm (4) 4cm、5cm、6cm
师生共同讨论解答如下:
解:
(1) 因为10cm+7cm>15cm, 所以这三条线段能组成一个三角形.
(2) 因为4cm+5cm<10cm,所以这三条线段不能组成一个三角形.
(3) 因为3cm+5cm=8cm, 所以这三条线段不能组成一个三角形.
(4) 因为4cm+5cm>6cm,所以这三条线段能组成一个三角形.
总结点拨:(出示课件21)只要满足较小的两条线段之和大于第三条线段,或较长线段与最短线段之差小于中间线段,便可构成三角形;若不满足,则不能构成三角形.
例3 用一根长为18厘米的细铁丝围成一个等腰三角形.
(1)如果腰长是底边的2倍,那么各边的长分别是多少?(出示课件23)
(2)能围成有一边的长为4厘米的等腰三角形吗?为什么?(出示课件24)
解 :
(1)设底边的长为x厘米,则腰长为2x厘米,
由题意得:x+2x+2x=18
解得x=3.6 ,
所以三边长分别为3.6厘米,7.2厘米,7.2厘米.
(2)因为长为4厘米的边可能是腰,也可能是底边,所以需要分两种情况讨论.
(a)因为长为4厘米的边为底边,设腰长为x厘米,则4+2x=18,解得x=7.
(b)因为长为4厘米的边为腰,设底边长为y厘米,则2×4+y=18,解得y=10.
因为4+4<10,出现两边和小于第三边的情况,所以不能围成腰长为4厘米的等腰三角形.由以上结论可以知道,可以围成底边是4厘米的等腰三角形.
出示课件25,引导学生思考。
出示课件26,学生自主思考并解答。
(三)课堂练习(出示课件27-31)
1. 下列长度的三条线段,能组成三角形的是( )
A.4cm,5cm,9cm B.8cm,8cm,15cm
C.5cm,5cm,10cm D.6cm,7cm,14cm
2.已知三角形两边的长分别是3和7,则此三角形第三边的长可能是( )
A.1 B.2 C.8 D.11
3. 如图,图中直角三角形共有( )
A.1个 B.2个 C.3个 D.4个
4.下列各组数中,能作为一个三角形三边边长的是( )
A.1,1,2 B.1,2,4
C.2,3,4 D.2,3,5
5.下列说法:①等边三角形是等腰三角形;②三角形按边分类可分为等腰三角形、等边三角形、不等边三角形;③三角形的两边之差大于第三边;④三角形按角分类应分为锐角三角形、直角三角形、钝角三角形. 其中正确的有( )
A.1个 B.2个 C.3个 D.4个
6.一个等腰三角形的周长为24cm,只知其中一边的长为7cm,则这个等腰三角形的腰长为_________cm.
7. “佳园工艺店”打算制作一批两边长分别是7分米,3分米,第三边长为奇数的不同规格的三角形木框。
(1)要制作满足上述条件的三角形木框共有几种.
(2)若每种规格的三角形木框只制作一个,制作这种木框的木条的售价为8元/分米,问至少需要多少钱购买材料 (忽略接头)
参考答案:
1.B
2.C 解析:设三角形第三边的长为x,由题意得:7–3<x<7+3,
4<x<10.
3.C
4.C
5.B
6.7或8.5
7.解:
(1)三角形的第三边x满足:7-3(2)制作这三种木框的木条的长为:3+5+7+3+7+7+3+7+9=51(分米),
所以51×8=408(元).
答:至少需要408元购买材料.
(四)课堂小结
今天我们学了哪些内容:
1.三角形的有关概念(边、角、顶点)。
2.会用符号表示一个三角形,会对三角形进行分类。
3.通过实践掌握三角形的三边不等关系。
(五)课前预习
预习下节课(11.1.2)的相关内容。
知道三角形中高、中线、角平分线的定义
七、课后作业
1、教材4页练习1,2
2、有两根长度分别为5 cm, 8 cm的木棒,用长度为2 cm的木棒与它们能摆成三角形吗?为什么?长度为13 cm的木棒呢?
板书设计:
九、教学反思:
本节的知识内容是在学生已经学习了一部分有关三角形的知识的基础上,对三角形进行更深入的研究.在教学过程中,教师不断引导学生以已有的知识为出发点进行深入思考,从而发现问题.
在教学设计上,注重学生自主学习、独立思考,注重交流合作,让学生利用自己已有的知识,在独立思考与交流合作中进行更深入的探究,使学生在经历整个探究过程后,能够更深入地理解和掌握三角形的概念及三边的关系,并获得数学活动的经验,提高探究能力和发现问题的能力.
11.1 与三角形有关的线段
11.1.1 三角形的边
第1课时 三角形的边
一、教学目标
【知识与技能】
1.进一步认识三角形的概念及其基本要素;
2.学会对三角形进行分类;
3.理解并掌握三角形三条边之间的关系。
【过程与方法】
经历度量三角形边长的实践活动,理解三角形三边不等的关系。
【情感态度与价值观】
帮助学生树立几何知识源于客观实际,用客观实际的观念,激发学生学习的兴趣。
二、课型
新授课
三、课时
第1课时
四、教学重难点
【教学重点】
理解三角形定义、证明三角形三边关系。
【教学难点】
1.在具体的图形中不重复,且不遗漏地识别所有三角形.
2.用三角形三边不等关系判定三条线段可否组成三角形.
五、课前准备
教师:课件、三角尺、屋顶架结构图等。
学生:三角尺、铅垂纸、小刀。
六、教学过程
(一)导入新课(出示课件2)
1. 你能从中找出4个不同的三角形吗?与同学交流各自找出的三角形.
2. 这些三角形有什么共同特点?
(二)探索新知
1.观察三角形的构成,探索三角形的概念(出示课件4)
教师问1:你能画出一个三角形吗?
让学生画出三角形,直观感受三角形的构成.
教师问2:结合你画的三角形,说明三角形是由什么组成的?
学生回答:三角形是由三条线段组成的.
教师问3:什么叫三角形?
学生回答:由三条线段组成的图形叫做三角形.
教师问4:如下图,是由三条线组成的图形,这样的图形是三角形吗?
学生回答:这样的不是三角形.
教师问5:你们讨论一下,如何给三角形下定义呢?
学生讨论回答:
需要满足以下条件:
三角形的特征有:
(1)三条线段;(2)不在同一直线上;(3)首尾顺次连接.
教师画出图形:如图所示:
教师归纳:由不在同一直线上的三条线段首尾顺次相接所组成的图形叫做三角形.(出示课件5)
2.自主学习三角形的表示方法及分类
阅读教材第2页到第3页探究前内容,回答下列问题.
教师问6:根据右图回答以下问题:
(1)在三角形中,什么叫边?什么叫内角?什么叫顶点?
学生回答:
如图:线段AB、BC、CA是△ABC的三边;
点A、B、C△ABC的三个顶点;
∠A、∠B、∠C是△ABC的三个内角.
教师总结(出示课件6):①边:组成三角形的每条线段叫做三角形的边. ②顶点:每两条线段的交点叫做三角形的顶点. ③内角:相邻两边组成的角.
(2)如何用小写字母表示三角形ABC的三条边?
学生回答:△ABC的边AB为∠C所对的边,可以用顶点C的小写字母c表示,同样,边AC可用b表示,边BC可用a表示.
教师出示下图边讲解:
(3)如何用符号表示三角形ABC (出示课件7)
学生回答:三角形用符号“△”表示. 记作“△ ABC”读作“三角形ABC”.
例 1: 说出图中有多少个三角形,用符号“△”表示,并指出每一个三角形的三条边,三个顶点,三个内角. (出示课件8)
师生共同讨论解答如下:
解:图中有3个三角形,分别是△EHG,△EHF,△EFG.
△EHG的三边是EH、HG、GE,三内角是
∠G、∠GHE、∠HEG,三个顶点是G、H、E;
△EHF的三边是EH、HF、FE,三内角
是∠EHF、∠HFE、∠HEF,三个
顶点是F、H、E;
△EFG的三边是EF、FG、GE,三内角是∠G、∠GFE、∠FEG,三个顶点是G、F、E.
总结点拨:(出示课件9)
在查三角形的个数时,先给单个三角形编号,查单个的三角形,再查两个三角形组成的较大三角形,然后再查三个,四个三角形组成的三角形.
出示课件10,找学生读出三角形。
教师问7:我们知道,三角形按角可以分为锐角三角形、直角三角形和钝角三角形.(如下所示)你能按照边的关系对三角形进行分类吗?(出示课件11)
学生回答:三角形按照“有几条边相等”可以分为:
学生问:按边分类后的特殊三角形之间有什么关系?它们的边和角怎样命名?
教师讲解:如下图:(出示课件12)
出示课件13,教师引导学生,根据已知条件,判断三角形的形状。
出示课件14,由学生讨论,并解答,教师总结给出答案。
3. 通过观察实践,理解三角形三边关系
教师问8:任意画一个△ABC,假设有一只小虫从点B出发,沿三角形的边爬到点C,它有几条线路可以选择?各条线路的长一样吗?
学生回答:小虫从点B出发沿三角形的边爬到点C有2条线路:(1)从B→C,即线段BC的长;(2)从B→A→C,即线段BA与线段AC长之和:BA+AC.
经过测量可得BA+AC>BC,所以这两条线路的长不一样.
根据“两点的所有连线中,线段最短”,说明BA+AC>BC.
教师讲解:由不等式的基本性质可得:AB>BC–AC.
教师问9:在A点的小狗,为了尽快吃到B点的香肠,它会选择哪条路线 如果小狗在C点呢?(出示课件15)
学生回答:从A→B,即线段AB的长;
教师问10:为什么呢?
学生回答:两点的所有连线中,线段最短.
教师问11:联系三角形的三边,从问题中你可以得到怎样的结论?(出示课件16)
学生回答:三角形两边的和大于第三边.
(出示课件17)
学生回答:三角形两边的差小于第三边.
(出示课件18-19,学生进行练习)
教师总结:三角形的三边有这样的关系:
(1) 三角形两边的和大于第三边.
(2) 三角形两边的差小于第三边.
例2 下列长度的各组线段能否组成一个三角形?(出示课件20)
(1)15cm、10cm、7cm (2) 4cm、5cm、10cm
(3) 3cm、8cm、5cm (4) 4cm、5cm、6cm
师生共同讨论解答如下:
解:
(1) 因为10cm+7cm>15cm, 所以这三条线段能组成一个三角形.
(2) 因为4cm+5cm<10cm,所以这三条线段不能组成一个三角形.
(3) 因为3cm+5cm=8cm, 所以这三条线段不能组成一个三角形.
(4) 因为4cm+5cm>6cm,所以这三条线段能组成一个三角形.
总结点拨:(出示课件21)只要满足较小的两条线段之和大于第三条线段,或较长线段与最短线段之差小于中间线段,便可构成三角形;若不满足,则不能构成三角形.
例3 用一根长为18厘米的细铁丝围成一个等腰三角形.
(1)如果腰长是底边的2倍,那么各边的长分别是多少?(出示课件23)
(2)能围成有一边的长为4厘米的等腰三角形吗?为什么?(出示课件24)
解 :
(1)设底边的长为x厘米,则腰长为2x厘米,
由题意得:x+2x+2x=18
解得x=3.6 ,
所以三边长分别为3.6厘米,7.2厘米,7.2厘米.
(2)因为长为4厘米的边可能是腰,也可能是底边,所以需要分两种情况讨论.
(a)因为长为4厘米的边为底边,设腰长为x厘米,则4+2x=18,解得x=7.
(b)因为长为4厘米的边为腰,设底边长为y厘米,则2×4+y=18,解得y=10.
因为4+4<10,出现两边和小于第三边的情况,所以不能围成腰长为4厘米的等腰三角形.由以上结论可以知道,可以围成底边是4厘米的等腰三角形.
出示课件25,引导学生思考。
出示课件26,学生自主思考并解答。
(三)课堂练习(出示课件27-31)
1. 下列长度的三条线段,能组成三角形的是( )
A.4cm,5cm,9cm B.8cm,8cm,15cm
C.5cm,5cm,10cm D.6cm,7cm,14cm
2.已知三角形两边的长分别是3和7,则此三角形第三边的长可能是( )
A.1 B.2 C.8 D.11
3. 如图,图中直角三角形共有( )
A.1个 B.2个 C.3个 D.4个
4.下列各组数中,能作为一个三角形三边边长的是( )
A.1,1,2 B.1,2,4
C.2,3,4 D.2,3,5
5.下列说法:①等边三角形是等腰三角形;②三角形按边分类可分为等腰三角形、等边三角形、不等边三角形;③三角形的两边之差大于第三边;④三角形按角分类应分为锐角三角形、直角三角形、钝角三角形. 其中正确的有( )
A.1个 B.2个 C.3个 D.4个
6.一个等腰三角形的周长为24cm,只知其中一边的长为7cm,则这个等腰三角形的腰长为_________cm.
7. “佳园工艺店”打算制作一批两边长分别是7分米,3分米,第三边长为奇数的不同规格的三角形木框。
(1)要制作满足上述条件的三角形木框共有几种.
(2)若每种规格的三角形木框只制作一个,制作这种木框的木条的售价为8元/分米,问至少需要多少钱购买材料 (忽略接头)
参考答案:
1.B
2.C 解析:设三角形第三边的长为x,由题意得:7–3<x<7+3,
4<x<10.
3.C
4.C
5.B
6.7或8.5
7.解:
(1)三角形的第三边x满足:7-3
所以51×8=408(元).
答:至少需要408元购买材料.
(四)课堂小结
今天我们学了哪些内容:
1.三角形的有关概念(边、角、顶点)。
2.会用符号表示一个三角形,会对三角形进行分类。
3.通过实践掌握三角形的三边不等关系。
(五)课前预习
预习下节课(11.1.2)的相关内容。
知道三角形中高、中线、角平分线的定义
七、课后作业
1、教材4页练习1,2
2、有两根长度分别为5 cm, 8 cm的木棒,用长度为2 cm的木棒与它们能摆成三角形吗?为什么?长度为13 cm的木棒呢?
板书设计:
九、教学反思:
本节的知识内容是在学生已经学习了一部分有关三角形的知识的基础上,对三角形进行更深入的研究.在教学过程中,教师不断引导学生以已有的知识为出发点进行深入思考,从而发现问题.
在教学设计上,注重学生自主学习、独立思考,注重交流合作,让学生利用自己已有的知识,在独立思考与交流合作中进行更深入的探究,使学生在经历整个探究过程后,能够更深入地理解和掌握三角形的概念及三边的关系,并获得数学活动的经验,提高探究能力和发现问题的能力.
