人教版七年级数学上册1.5.1乘方-课件(共22张PPT)
文档属性
| 名称 | 人教版七年级数学上册1.5.1乘方-课件(共22张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 798.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-18 17:50:01 | ||
图片预览







文档简介
(共22张PPT)
1.5 有理数的乘方(第1课时)
1.5.1 有理数的乘方
课件说明
本节课学习有理数乘方的意义,乘方运算.
学习目标:
利用有理数的乘方进行运算及有理数的混合运算.
学习重点:
有理数乘方的表示方法及运算.
1次
2次
20次
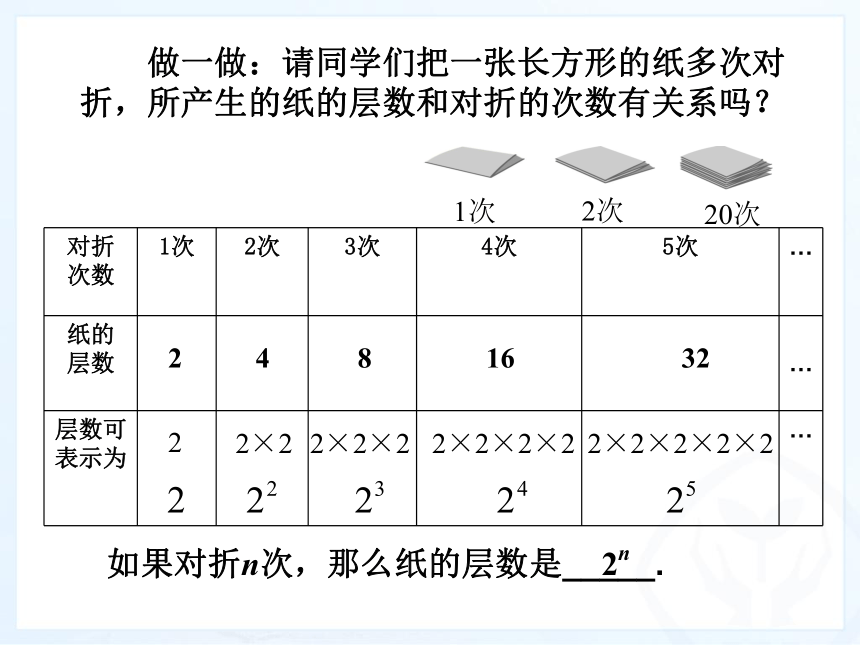
做一做:请同学们把一张长方形的纸多次对折,所产生的纸的层数和对折的次数有关系吗?
对折
次数 1次 2次 3次 4次 5次 …
纸的
层数
…
层数可
表示为 …
2
4
8
16
32
2
2×2×2
2×2×2×2
2×2×2×2×2
2×2
如果对折n次,那么纸的层数是_____.
2n
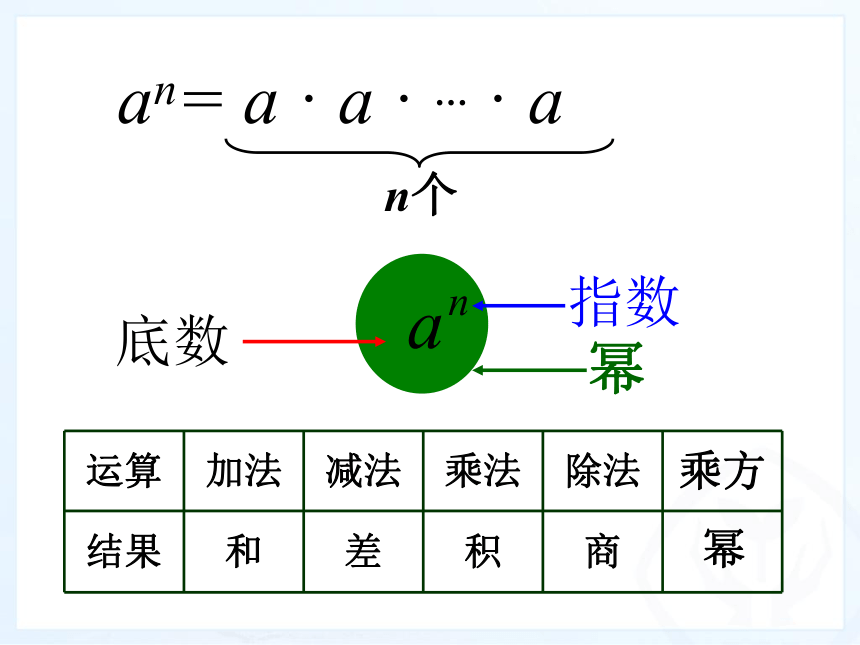
一般地,n个相同的因数a相乘,即
求n个相同因数的积的运算叫做
乘方,乘方的结果叫幂.
,记作 ,读作
a的n次方.
n个
a · a · … · a
底数
指数
幂
运算 加法 减法 乘法 除法 乘方
结果 和 差 积 商
幂
n个
an= a · a · … · a
例1 说出下列乘方的底数、指数且计算:
(1) (-4)3; (2) (-2)4;
(3) 07; (4) .
(2) (-2)4 =(-2)×(-2)×(-2)×(-2)=16;
(3) 07 =0×0×0×0 × 0×0×0=0;
(1) (-4)3 =(-4)×(-4)×(-4)=-64;
解:
(4)
计算:102 , 103 , 104.
解:(1)102
=10×10=
100;
103 =
10 ×10×10
= 1 000;
(2)
104 =
10 ×10×10 ×10
=10 000.
(3)
答:10的几次方,幂的结果中1后面就有几个0.
观察结果,你能发现什么规律?
想一想:
(1)负数的乘方,在书写时一定要把整个负数(连同符号),用小括号括起来.这也是辨认底数的方法;
(2)分数的乘方,在书写时一定要把整个分数用小括号括起来.
由上题中
你有什么发现?
和
你能迅速判断下列各幂的正负吗?
你能用计算器计算 和 吗?
我们学习了哪些运算?
加法、减法、乘法、除法、乘方
一个运算中,含有有理数的加、减、乘、除、乘方等多种运算,称为有理数的混合运算.
问:算式含有哪几种运算
观察
加减运算
乘方运算
第一级运算
第三级运算
乘除运算
第二级运算
一题多解:
解法一:原式
解法二:原式
哪种更简便?
计算:
理解
议一议,说一说:
?
?
?
观察下列三行数,你能提出哪些问题?
-2,4,-8,16,-32,64,… ①
0,6,-6,18,-30,66,… ②
-1,2,-4,8,-16,32,… ③
第②行
第③行
(1)第①行数按什么规律排列?
(2)第②③行数与第①行数分别有什么关系?
解:
(1)
(2)
观察下列三行数,你能提出哪些问题?
-2,4,-8,16,-32,64,…①
0,6,-6,18,-30,66,… ②
-1,2,-4,8,-16,32,… ③
(3)取每行数的第10个数,计算这三个数的和.
解:
(3)
辨析:
解:原式
正确解法:
解:原式
不计算下列各式的值,你能确定其符号吗?
你能得到什么规律吗?说出你的根据.
(1)(-2)51 ;(2)(-2)50;(3)250;
(4)251; (5)02 012 ; (6)12 013.
归纳:
(1)正数的任何次幂是正数;
(2)负数的偶次幂是正数;负数的奇次幂是负数;
(3)0的任何次幂等于零;
(4)1的任何次幂等于1.
(4) ;( )
判断:(对的画“√”,错的画“×”.)
(1) 32 = 3×2 = 6;( )
(2) (-2)3 = (-3)2; ( )
(3) -32 = (-3)2;( )
(5) . ( )
×
32 = 3×3=9
(-2)3=-8;(-3)2=9
-32 =-9; (-3)2=9
-24=-2×2×2×2=-16
×
×
×
×
(2)
(1)
(3)
(4)
(5)
1.教科书习题1.5复习巩固第1,3题;
2.补充题
课后作业
1.5 有理数的乘方(第1课时)
1.5.1 有理数的乘方
课件说明
本节课学习有理数乘方的意义,乘方运算.
学习目标:
利用有理数的乘方进行运算及有理数的混合运算.
学习重点:
有理数乘方的表示方法及运算.
1次
2次
20次
做一做:请同学们把一张长方形的纸多次对折,所产生的纸的层数和对折的次数有关系吗?
对折
次数 1次 2次 3次 4次 5次 …
纸的
层数
…
层数可
表示为 …
2
4
8
16
32
2
2×2×2
2×2×2×2
2×2×2×2×2
2×2
如果对折n次,那么纸的层数是_____.
2n
一般地,n个相同的因数a相乘,即
求n个相同因数的积的运算叫做
乘方,乘方的结果叫幂.
,记作 ,读作
a的n次方.
n个
a · a · … · a
底数
指数
幂
运算 加法 减法 乘法 除法 乘方
结果 和 差 积 商
幂
n个
an= a · a · … · a
例1 说出下列乘方的底数、指数且计算:
(1) (-4)3; (2) (-2)4;
(3) 07; (4) .
(2) (-2)4 =(-2)×(-2)×(-2)×(-2)=16;
(3) 07 =0×0×0×0 × 0×0×0=0;
(1) (-4)3 =(-4)×(-4)×(-4)=-64;
解:
(4)
计算:102 , 103 , 104.
解:(1)102
=10×10=
100;
103 =
10 ×10×10
= 1 000;
(2)
104 =
10 ×10×10 ×10
=10 000.
(3)
答:10的几次方,幂的结果中1后面就有几个0.
观察结果,你能发现什么规律?
想一想:
(1)负数的乘方,在书写时一定要把整个负数(连同符号),用小括号括起来.这也是辨认底数的方法;
(2)分数的乘方,在书写时一定要把整个分数用小括号括起来.
由上题中
你有什么发现?
和
你能迅速判断下列各幂的正负吗?
你能用计算器计算 和 吗?
我们学习了哪些运算?
加法、减法、乘法、除法、乘方
一个运算中,含有有理数的加、减、乘、除、乘方等多种运算,称为有理数的混合运算.
问:算式含有哪几种运算
观察
加减运算
乘方运算
第一级运算
第三级运算
乘除运算
第二级运算
一题多解:
解法一:原式
解法二:原式
哪种更简便?
计算:
理解
议一议,说一说:
?
?
?
观察下列三行数,你能提出哪些问题?
-2,4,-8,16,-32,64,… ①
0,6,-6,18,-30,66,… ②
-1,2,-4,8,-16,32,… ③
第②行
第③行
(1)第①行数按什么规律排列?
(2)第②③行数与第①行数分别有什么关系?
解:
(1)
(2)
观察下列三行数,你能提出哪些问题?
-2,4,-8,16,-32,64,…①
0,6,-6,18,-30,66,… ②
-1,2,-4,8,-16,32,… ③
(3)取每行数的第10个数,计算这三个数的和.
解:
(3)
辨析:
解:原式
正确解法:
解:原式
不计算下列各式的值,你能确定其符号吗?
你能得到什么规律吗?说出你的根据.
(1)(-2)51 ;(2)(-2)50;(3)250;
(4)251; (5)02 012 ; (6)12 013.
归纳:
(1)正数的任何次幂是正数;
(2)负数的偶次幂是正数;负数的奇次幂是负数;
(3)0的任何次幂等于零;
(4)1的任何次幂等于1.
(4) ;( )
判断:(对的画“√”,错的画“×”.)
(1) 32 = 3×2 = 6;( )
(2) (-2)3 = (-3)2; ( )
(3) -32 = (-3)2;( )
(5) . ( )
×
32 = 3×3=9
(-2)3=-8;(-3)2=9
-32 =-9; (-3)2=9
-24=-2×2×2×2=-16
×
×
×
×
(2)
(1)
(3)
(4)
(5)
1.教科书习题1.5复习巩固第1,3题;
2.补充题
课后作业
