人教版八年级数学上册12.2 三角形全等的判定(“角角边”判定三角形全等)教学设计
文档属性
| 名称 | 人教版八年级数学上册12.2 三角形全等的判定(“角角边”判定三角形全等)教学设计 |

|
|
| 格式 | docx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-18 00:00:00 | ||
图片预览

文档简介
课 题:三角形全等的判定(“ASA”、“AAS”)
教学目标:【知识与技能】掌握三角形全等的“角边角”“角角边”条件,会应用解决简单的推理证明题;
【过程与方法】能从题设或结论出发,寻找论证思路,学会用综合法证明问题;
【情感、态度与价值观】通过画图、探究、归纳、交流,展示,使学生获得一些研究问题的经验和方法,提升实践能力,验成功的快乐。
学情分析:本节课是学生经历了动手实践、观察猜想、归纳总结等过程获得SSS和SAS判定方法之后,继续探索三角形全等的条件.在教学时可引导学生类比前面的探究方法自主得到ASA和AAS判定方法,因为学生在研究几何图形的方法和合情推理方面还存在欠缺.特别是运用数学结论的思想较弱,思维的广阔性、敏捷性、灵活性比较欠缺,在解题过程中,找全等条件又是一个难点。因此在教学过程中,教师要特别关注学生清晰地表达数学思考的过程,分析图形之间的内在联系,将分析问题,解决问题落到实处。这样即可加深学生对已学定理的认识,又可以从中感悟三角形全等的数学本质,从中积累数学活动经验。
教学重、难点:重点是用ASA和AAS的方法证明两个三角形全等及规范书写格式;难点是分析、寻找证明三角形全等的条件。
教学方法:“学、议、展、评、练、结、思”
教学过程:
☆温故知新(3分钟)☆
(1)如果两个三角形满足三个对应元素相等,,包括哪几种情况 (三个角、三个边、两边一角、两角一边.)。可以出现哪些组合
( SSS SAS SSA ASA AAS AAA)
(2)到目前为止,可以作为判别两三角形全等的方法有几种 各是什么 (三种:①定义;②SSS;③SAS.)但满足SSA的两个三角形不一定全等,(举例说明)
(3).若AB=AC,则添加一个什么条件可得△ABD≌ △ACD
(4)想一想:两个三角形满足 ASA 或AAS或AAA条件,这两上三角形能否相等呢
☆教师导学☆在前面的学习中,我们通过动手画图、观察猜想、总结归纳,对三角形全等的条件进行了探究.主要研究了“两边一角”对应相等的情况,得到了两种判定两个三角形全等的方法,本节课,继续探究“两角一边”对应相等的情况。
☆我阅读我实践☆用15分钟自学课本P39—41页的内容,并完成下列题目
1.动手试一试(在草稿纸上作图)已知:△ABC,画一个△A’B’C’,
使A’B’=AB,∠A’=∠A,∠B’=∠B. (P39)
作法:(1). 画A’B’=AB;
(2). 在A’B’的同旁画∠DA’B’=∠A,
∠EB’A’ =∠B,A’D,B’E交于点C’.
∴△A’B’C’为所求作的三角形.
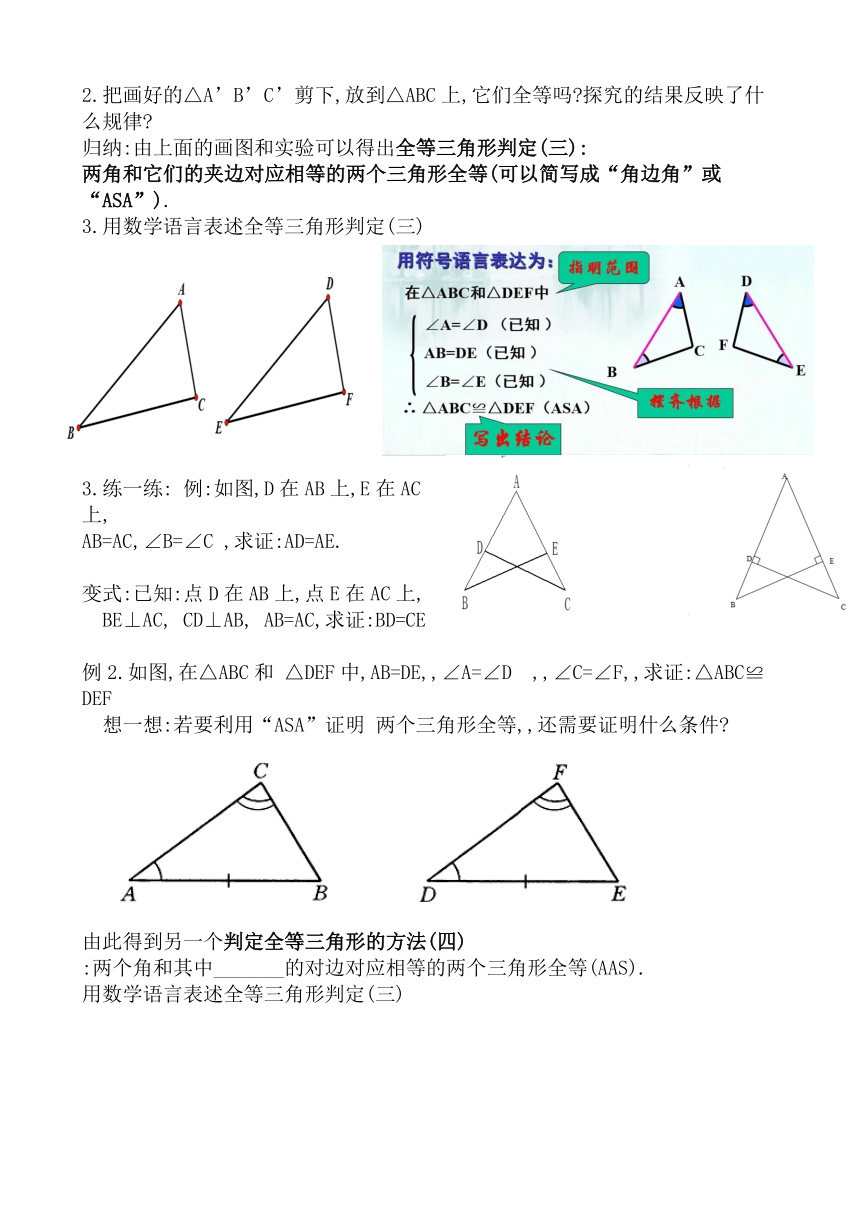
2.把画好的△A’B’C’剪下,放到△ABC上,它们全等吗 探究的结果反映了什么规律
归纳:由上面的画图和实验可以得出全等三角形判定(三):
两角和它们的夹边对应相等的两个三角形全等(可以简写成“角边角”或“ASA”).
3.用数学语言表述全等三角形判定(三)
3.练一练: 例:如图,D在AB上,E在AC上,
AB=AC,∠B=∠C ,求证:AD=AE.
变式:已知:点D在AB上,点E在AC上,
BE⊥AC, CD⊥AB, AB=AC,求证:BD=CE
例2.如图,在△ABC和 △DEF中,AB=DE,,∠A=∠D ,,∠C=∠F,,求证:△ABC≌DEF
想一想:若要利用“ASA”证明 两个三角形全等,,还需要证明什么条件
由此得到另一个判定全等三角形的方法(四)
:两个角和其中_______的对边对应相等的两个三角形全等(AAS).
用数学语言表述全等三角形判定(三)
☆合作探究☆(5分钟)
思考1:若两个角和一条边分别相等的两个三角形全等吗
思考2:三个角分别相等的两个三角形全等吗
☆精彩纷呈☆(20分钟)
1、已知△ABC和△ A′B′C′中,AB=A′B′,∠A=∠A′,∠B=∠B′, 则△ABC≌△ A′B′C′的根据是( )
A、SAS B、ASA C、AAS D、都不对
2、已知: △ABC和△A′B′C ′中,AB=A′B′,∠A=∠A′, 若△ABC≌△ A′B′C′,还需要什么条件( )
A、∠B=∠B′ B、∠C=∠C′
C、AC=A′C′ D、A、B、C均可
3、如图,AD=BC , AC=′BD,则图中全等三角形有( )
A.1对 B.2对 C.3对 D.4对
4.如图,AD和BE相交于点O ,已知:∠A = ∠E. ,请添加一个条件_________.,使AB=′CD ,理由是___________.
5、已知:如图:∠B=∠DEF, BC=EF, 求证:ΔABC≌ ΔDEF
(1)若要以“SAS”为依据,还缺条件 ___________;
(2)若要以“ASA”为依据,还缺条件 ___________;
(3)若要以“SSS” 为依据,还缺条件___________;
(4)若要以“AAS” 为依据,还缺条件___________.
6、已知∠1=∠2,∠3= ∠4, 求证:BD=BE.
归纳小结 (2分钟)
1.课件归纳:
2.推证两三角形全等时,要善于观察,寻求对应相等的条件,从而获得解题途径.注意公共角或公共边为一组相等的对应角或边的隐含条件.
3.证明线段相等、角相等问题的基本途径是证明它们所在的三角形全等.
4.方法点拨:证明过程中,确定判定方法后,找缺少什么条件,则转化为先证明所缺条件成立,再写证明两个三角形全等过程.
课后展示:课本41页1题、2题,11题、12题,44页5题,12题
教后反思:学生有了先学微课的基础,在课上接受的内容较好,教师只须点拨到位,学生便可顺利的展示,学生在展示的过程中会出现各样的不足,这也正是引导学生使学习走向深入所在。小结时注重知识的归类,方法的提升就可使学生很好的掌握所学的内容!
教学目标:【知识与技能】掌握三角形全等的“角边角”“角角边”条件,会应用解决简单的推理证明题;
【过程与方法】能从题设或结论出发,寻找论证思路,学会用综合法证明问题;
【情感、态度与价值观】通过画图、探究、归纳、交流,展示,使学生获得一些研究问题的经验和方法,提升实践能力,验成功的快乐。
学情分析:本节课是学生经历了动手实践、观察猜想、归纳总结等过程获得SSS和SAS判定方法之后,继续探索三角形全等的条件.在教学时可引导学生类比前面的探究方法自主得到ASA和AAS判定方法,因为学生在研究几何图形的方法和合情推理方面还存在欠缺.特别是运用数学结论的思想较弱,思维的广阔性、敏捷性、灵活性比较欠缺,在解题过程中,找全等条件又是一个难点。因此在教学过程中,教师要特别关注学生清晰地表达数学思考的过程,分析图形之间的内在联系,将分析问题,解决问题落到实处。这样即可加深学生对已学定理的认识,又可以从中感悟三角形全等的数学本质,从中积累数学活动经验。
教学重、难点:重点是用ASA和AAS的方法证明两个三角形全等及规范书写格式;难点是分析、寻找证明三角形全等的条件。
教学方法:“学、议、展、评、练、结、思”
教学过程:
☆温故知新(3分钟)☆
(1)如果两个三角形满足三个对应元素相等,,包括哪几种情况 (三个角、三个边、两边一角、两角一边.)。可以出现哪些组合
( SSS SAS SSA ASA AAS AAA)
(2)到目前为止,可以作为判别两三角形全等的方法有几种 各是什么 (三种:①定义;②SSS;③SAS.)但满足SSA的两个三角形不一定全等,(举例说明)
(3).若AB=AC,则添加一个什么条件可得△ABD≌ △ACD
(4)想一想:两个三角形满足 ASA 或AAS或AAA条件,这两上三角形能否相等呢
☆教师导学☆在前面的学习中,我们通过动手画图、观察猜想、总结归纳,对三角形全等的条件进行了探究.主要研究了“两边一角”对应相等的情况,得到了两种判定两个三角形全等的方法,本节课,继续探究“两角一边”对应相等的情况。
☆我阅读我实践☆用15分钟自学课本P39—41页的内容,并完成下列题目
1.动手试一试(在草稿纸上作图)已知:△ABC,画一个△A’B’C’,
使A’B’=AB,∠A’=∠A,∠B’=∠B. (P39)
作法:(1). 画A’B’=AB;
(2). 在A’B’的同旁画∠DA’B’=∠A,
∠EB’A’ =∠B,A’D,B’E交于点C’.
∴△A’B’C’为所求作的三角形.
2.把画好的△A’B’C’剪下,放到△ABC上,它们全等吗 探究的结果反映了什么规律
归纳:由上面的画图和实验可以得出全等三角形判定(三):
两角和它们的夹边对应相等的两个三角形全等(可以简写成“角边角”或“ASA”).
3.用数学语言表述全等三角形判定(三)
3.练一练: 例:如图,D在AB上,E在AC上,
AB=AC,∠B=∠C ,求证:AD=AE.
变式:已知:点D在AB上,点E在AC上,
BE⊥AC, CD⊥AB, AB=AC,求证:BD=CE
例2.如图,在△ABC和 △DEF中,AB=DE,,∠A=∠D ,,∠C=∠F,,求证:△ABC≌DEF
想一想:若要利用“ASA”证明 两个三角形全等,,还需要证明什么条件
由此得到另一个判定全等三角形的方法(四)
:两个角和其中_______的对边对应相等的两个三角形全等(AAS).
用数学语言表述全等三角形判定(三)
☆合作探究☆(5分钟)
思考1:若两个角和一条边分别相等的两个三角形全等吗
思考2:三个角分别相等的两个三角形全等吗
☆精彩纷呈☆(20分钟)
1、已知△ABC和△ A′B′C′中,AB=A′B′,∠A=∠A′,∠B=∠B′, 则△ABC≌△ A′B′C′的根据是( )
A、SAS B、ASA C、AAS D、都不对
2、已知: △ABC和△A′B′C ′中,AB=A′B′,∠A=∠A′, 若△ABC≌△ A′B′C′,还需要什么条件( )
A、∠B=∠B′ B、∠C=∠C′
C、AC=A′C′ D、A、B、C均可
3、如图,AD=BC , AC=′BD,则图中全等三角形有( )
A.1对 B.2对 C.3对 D.4对
4.如图,AD和BE相交于点O ,已知:∠A = ∠E. ,请添加一个条件_________.,使AB=′CD ,理由是___________.
5、已知:如图:∠B=∠DEF, BC=EF, 求证:ΔABC≌ ΔDEF
(1)若要以“SAS”为依据,还缺条件 ___________;
(2)若要以“ASA”为依据,还缺条件 ___________;
(3)若要以“SSS” 为依据,还缺条件___________;
(4)若要以“AAS” 为依据,还缺条件___________.
6、已知∠1=∠2,∠3= ∠4, 求证:BD=BE.
归纳小结 (2分钟)
1.课件归纳:
2.推证两三角形全等时,要善于观察,寻求对应相等的条件,从而获得解题途径.注意公共角或公共边为一组相等的对应角或边的隐含条件.
3.证明线段相等、角相等问题的基本途径是证明它们所在的三角形全等.
4.方法点拨:证明过程中,确定判定方法后,找缺少什么条件,则转化为先证明所缺条件成立,再写证明两个三角形全等过程.
课后展示:课本41页1题、2题,11题、12题,44页5题,12题
教后反思:学生有了先学微课的基础,在课上接受的内容较好,教师只须点拨到位,学生便可顺利的展示,学生在展示的过程中会出现各样的不足,这也正是引导学生使学习走向深入所在。小结时注重知识的归类,方法的提升就可使学生很好的掌握所学的内容!
