人教版七年级数学上册3.4 实际问题与一元一次方程-配套问题 课件(共15张PPT)
文档属性
| 名称 | 人教版七年级数学上册3.4 实际问题与一元一次方程-配套问题 课件(共15张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-18 00:00:00 | ||
图片预览






文档简介
(共15张PPT)
七年级上册
3.4实际问题与一元一次方程
——配套问题
从前面学习解方程的过程中可以看出,方程是分析和解决问题的一种很有用的数学工具。本节课我们就重点讨论如何用一元一次方程解决实际问题。
问题:尝试解决下面问题.
例 某车间有24名工人,每人每天可以生产1 200个螺钉,或2 000个螺母. 1个螺钉需要配1个螺母,为使每天生产的螺钉和螺母刚好配套,应安排生产螺钉和螺母的工人各多少名?
典型探究
解:设应安排x名工人生产螺钉,则(24-x)名工人生产螺母. 依题意得 :
1 200x = 2 000(24-x) .
3x= 5(24-x)
3x =120-5x
x=15
24-x=9.
答:应安排15名工人生产螺钉,9名工人生产螺母.
典型探究
变式:尝试解决下面问题
例 某车间有22名工人,每人每天可以生产1 200个螺钉,或2 000个螺母. 1个螺钉需要配2个螺母,为使每天生产的螺钉和螺母刚好配套,应安排生产螺钉和螺母的工人各多少名?
典型探究
22
2
典型探究
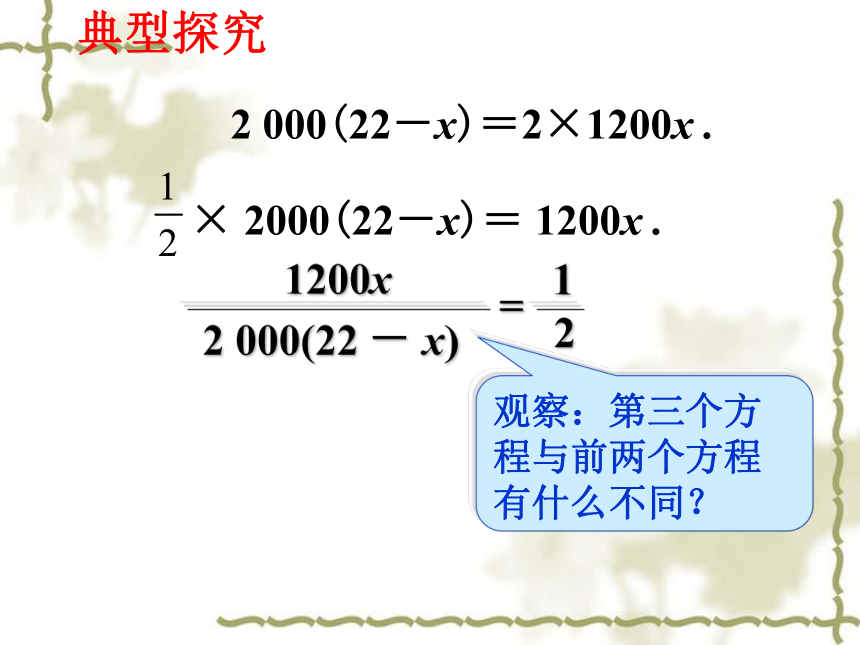
× 2000(22-x)= 1200x .
2 000(22-x)=2×1200x .
观察:第三个方程与前两个方程有什么不同?
1200x
2 000(22 - x)
=
1
2
列方程解决应用问题,其大致步骤有哪些?
1.审:审题,分析题目中的数量关系;
2.设:设未知数,并表示相关的数量关系;
3.列:根据题目中的等量关系列方程;
4.解:解这个方程;
5.答:检验方程的解是否符合题意并作答.
小结:
玩过拉力器吗?
提出问题
B
A
此拉力器由两个拉手A和五个弹簧B构成.
生产拉力器的厂家,会根据这里的配比关系安排工人生产拉手A和弹簧B的。同时厂家也会根据市场的需要调整弹簧的个数来满足更多群体的需要,这就会涉及比较多的配套问题。
提出问题
内容拓展
小组讨论
1、2个A和1个B配成一套,则A:B= ,
转化为一元一次方程为: ;
2、2个A和3个B配成一套,则A:B= ,
转化为一元一次方程为: ;
3、2个A和5个B配成一套,则A:B= ,
转化为一元一次方程为: ;
4、m个A和n个B配成一套,则A:B= ,
转化为一元一次方程为: ;
2:1
A=2B
2:3
2:5
m:n
3A=2B
5A=2B
nA=mB
拉力器由两个拉手和五个弹簧构成.用1 块钢材可以做12个拉手或5个弹簧. 现要用14块钢材制作这种仪器,需要用多少块钢材做拉手,多少块钢材做弹簧,恰好配成多少套拉力器?
解:设需要用 x 块钢材做拉手,(14-x) 块钢材做弹簧. 依题意得:
5×12 x=2×5 (14-x).
x=2,
14-x=12.
12×2÷2=12(套)
答:需要用2块钢材做拉手,12 块钢材做弹簧,恰好能配成12套拉力器.
解决问题
练习:
《课本》101页练习第1题。
1、一套仪器由一个A部件和三个B部件构成。用1m 钢材可做40个A部件或240个B部件。现要用6m 的钢材制作这种仪器,应用多少钢材做A部件,多少钢材做B部件,恰好配成这种仪器多少套?
(只设未知数,列出方程)
练习:
《课本》106页复习巩固第2题。
2、制作一张桌子要用一个桌面和4条桌腿,1m 木材可制作20个桌面,或者制作400条桌腿,现有12m 木材,应怎样计划用料才能制作尽可能多的桌子?
(只设未知数,列出方程)
1.本节课学习的主要内容是什么?
2.配套问题中m个A与n个B配套,
得 转化为: .
小结
A:B=m:n
nA=mB
实际问题
一元一次方程
设未知数,列方程
解方程
一元一次方程的解(x = a)
实际问题的答案
检 验
3.用一元一次方程解决实际问题的基本过程是什么?
七年级上册
3.4实际问题与一元一次方程
——配套问题
从前面学习解方程的过程中可以看出,方程是分析和解决问题的一种很有用的数学工具。本节课我们就重点讨论如何用一元一次方程解决实际问题。
问题:尝试解决下面问题.
例 某车间有24名工人,每人每天可以生产1 200个螺钉,或2 000个螺母. 1个螺钉需要配1个螺母,为使每天生产的螺钉和螺母刚好配套,应安排生产螺钉和螺母的工人各多少名?
典型探究
解:设应安排x名工人生产螺钉,则(24-x)名工人生产螺母. 依题意得 :
1 200x = 2 000(24-x) .
3x= 5(24-x)
3x =120-5x
x=15
24-x=9.
答:应安排15名工人生产螺钉,9名工人生产螺母.
典型探究
变式:尝试解决下面问题
例 某车间有22名工人,每人每天可以生产1 200个螺钉,或2 000个螺母. 1个螺钉需要配2个螺母,为使每天生产的螺钉和螺母刚好配套,应安排生产螺钉和螺母的工人各多少名?
典型探究
22
2
典型探究
× 2000(22-x)= 1200x .
2 000(22-x)=2×1200x .
观察:第三个方程与前两个方程有什么不同?
1200x
2 000(22 - x)
=
1
2
列方程解决应用问题,其大致步骤有哪些?
1.审:审题,分析题目中的数量关系;
2.设:设未知数,并表示相关的数量关系;
3.列:根据题目中的等量关系列方程;
4.解:解这个方程;
5.答:检验方程的解是否符合题意并作答.
小结:
玩过拉力器吗?
提出问题
B
A
此拉力器由两个拉手A和五个弹簧B构成.
生产拉力器的厂家,会根据这里的配比关系安排工人生产拉手A和弹簧B的。同时厂家也会根据市场的需要调整弹簧的个数来满足更多群体的需要,这就会涉及比较多的配套问题。
提出问题
内容拓展
小组讨论
1、2个A和1个B配成一套,则A:B= ,
转化为一元一次方程为: ;
2、2个A和3个B配成一套,则A:B= ,
转化为一元一次方程为: ;
3、2个A和5个B配成一套,则A:B= ,
转化为一元一次方程为: ;
4、m个A和n个B配成一套,则A:B= ,
转化为一元一次方程为: ;
2:1
A=2B
2:3
2:5
m:n
3A=2B
5A=2B
nA=mB
拉力器由两个拉手和五个弹簧构成.用1 块钢材可以做12个拉手或5个弹簧. 现要用14块钢材制作这种仪器,需要用多少块钢材做拉手,多少块钢材做弹簧,恰好配成多少套拉力器?
解:设需要用 x 块钢材做拉手,(14-x) 块钢材做弹簧. 依题意得:
5×12 x=2×5 (14-x).
x=2,
14-x=12.
12×2÷2=12(套)
答:需要用2块钢材做拉手,12 块钢材做弹簧,恰好能配成12套拉力器.
解决问题
练习:
《课本》101页练习第1题。
1、一套仪器由一个A部件和三个B部件构成。用1m 钢材可做40个A部件或240个B部件。现要用6m 的钢材制作这种仪器,应用多少钢材做A部件,多少钢材做B部件,恰好配成这种仪器多少套?
(只设未知数,列出方程)
练习:
《课本》106页复习巩固第2题。
2、制作一张桌子要用一个桌面和4条桌腿,1m 木材可制作20个桌面,或者制作400条桌腿,现有12m 木材,应怎样计划用料才能制作尽可能多的桌子?
(只设未知数,列出方程)
1.本节课学习的主要内容是什么?
2.配套问题中m个A与n个B配套,
得 转化为: .
小结
A:B=m:n
nA=mB
实际问题
一元一次方程
设未知数,列方程
解方程
一元一次方程的解(x = a)
实际问题的答案
检 验
3.用一元一次方程解决实际问题的基本过程是什么?
