数学人教A版(2019)选择性必修第一册2.2.3直线的一般式方程(课件共15张ppt)
文档属性
| 名称 | 数学人教A版(2019)选择性必修第一册2.2.3直线的一般式方程(课件共15张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-17 08:41:10 | ||
图片预览






文档简介
(共15张PPT)
第2章 直线和圆的方程
2.2.3 直线的一般式方程
思考:
(1)平面直角坐标系中任意一条直线都可以用一个关于x,y的二元一次方程表示吗?
(2)任意一个关于的二元一次方程都可以表示直线吗?
任意直线l经过点P0(x0,y0)
若直线l斜率不存在,即直线的倾斜角为90°时,直线的方程为=0
若直线l斜率存在,设直线的斜率为k,直线的方程为y-y0=k(x-x0).
关于x,y的二元一次方程
√
对于任意一个关于的二元一次方程
若,方程可变形为
若,方程可变形为
直线
√
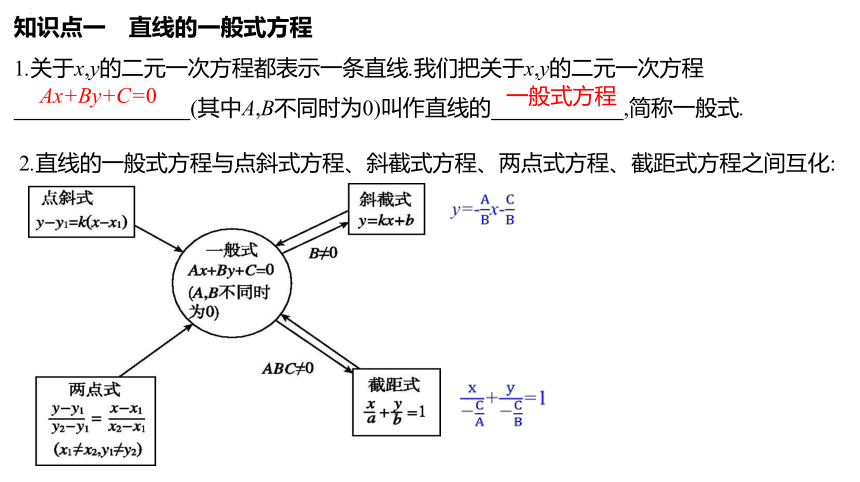
1.关于x,y的二元一次方程都表示一条直线.我们把关于x,y的二元一次方程
(其中A,B不同时为0)叫作直线的 ,简称一般式.
知识点一 直线的一般式方程
Ax+By+C=0
一般式方程
2.直线的一般式方程与点斜式方程、斜截式方程、两点式方程、截距式方程之间互化:
y=-x-
+=1
思考:
在方程Ax+By+C=0中,系数A,B,C为何值时,表示的直线:
平行于x轴:
平行于y轴:
与x轴重合:
与y轴重合:
与x轴、y轴都相交:
过原点:
A=0,B ,C
A,B =0,C
A=0,B ,C
A,B =0,C
A·B≠0
C=0
知识点二 二元一次方程与直线
在平面直角坐标系中,任意一个二元一次方程是直角坐标平面上一条确定的直线;反之,直角坐标平面上的任意一条直线可以用一个确定的二元一次方程表示.
例:点集{(x,y)|x+y-1=0}表示的图形是直线x+y-1=0.
探究点一 求直线的一般式方程
例1 (1)直线2x-y-2=0绕它与y轴的交点A按逆时针方向旋转所得的直线的方程是 ( )
A.x-2y+4=0 B.x+2y-4=0 C.x-2y-4=0 D.x+2y+4=0
D
(2)根据下列各条件写出直线的方程,并化成一般式.
①斜率是-,且经过点A(8,-6)的直线的方程为 .
②经过点B(4,2),且平行于x轴的直线的方程为 .
③在x轴和y轴上的截距分别是和-3的直线的方程为 .
④经过点P1(3,-2),P2(5,-4)的直线的方程为 .
x+2y+4=0
y-2=0
2x-y-3=0
x+y-1=0
探究点二 含参数的直线一般式方程的有关问题
解:(1)当m+1=0,即m=-1时,直线l1的斜率k1不存在,直线l2的斜率k2=,两直线不平行;
当m+1≠0,即m≠-1时,将两直线方程化为斜截式,可得l1:y=-x-,l2:y=-x+.
由l1∥l2知两直线斜率相等,在y轴上的截距不相等,所以-=-,且-≠,
解得m=2或m=-3,符合题意。
综上所述,m的值为2或-3.
例2 (1)直线l1:2x+(m+1)y+4=0与直线l2:mx+3y-2=0平行,求m的值;
若l1∥l2 A1B2-A2B1=0且B1C2-B2C1≠0(或A1C2-A2C1≠0).
(2)直线l1:ax+(1-a)y-3=0与直线l2:(a-1)x+(2a+3)y-2=0垂直,求a的值.
解:(2)当a=1时,l1:x=3,l2:y=,所以l1⊥l2;
当a=-时,l1:y=x+,l2:x=-,所以l1不垂直于l2;
当a≠1且a≠-时,k1=,k2=,由于l1⊥l2,则·=-1,可得a=-3.
综上可知,当a=1或a=-3时,l1⊥l2.
若l1⊥l2 A1A2+B1B2=0.
[小结]
(1)直线l1:A1x+B1y+C1=0,直线l2:A2x+B2y+C2=0,
①若l1∥l2 A1B2-A2B1=0且B1C2-B2C1≠0(或A1C2-A2C1≠0).
②若l1⊥l2 A1A2+B1B2=0.
(2)与直线Ax+By+C=0平行的直线方程可设为 Ax+By+C1=0(C1≠C);
与直线Ax+By+C=0垂直的直线方程可设为Bx-Ay+C2=0.
解:(1)证明:直线方程(2-m)x+(2m+1)y+3m+4=0可化为(2x+y+4)+m(-x+2y+3)=0,
由题意知该方程对任意m都成立,
所以解得所以直线恒过定点(-1,-2).
例3 已知直线方程为(2-m)x+(2m+1)y+3m+4=0.
(1)证明:直线恒过定点;
(2)若直线分别与x轴、y轴的负半轴交于A,B两点,求△AOB面积的最小值及此时直线的方程.
例3 已知直线方程为(2-m)x+(2m+1)y+3m+4=0.
(1)证明:直线恒过定点;
(2)若直线分别与x轴、y轴的负半轴交于A,B两点,求△AOB面积的最小值及此时直线的方程.
(2)方法一:
由(1)知直线过定点(-1,-2),结合题意可设直线的方程为y+2=k(x+1),k<0,则A (-1,0) ,B(0,k-2),
所以S△AOB= |-1| |k-2|= (-1) (k-2)=2+ (+) ≥2+2=4,
当且仅当k=-2时取等号,所以△AOB面积的最小值为4,
此时直线的方程为2x+y+4=0.
例3 已知直线方程为(2-m)x+(2m+1)y+3m+4=0.
(1)证明:直线恒过定点;
(2)若直线分别与x轴、y轴的负半轴交于A,B两点,求△AOB面积的最小值及此时直线的方程.
方法二:
设A(a,0),B(0,b),显然a<0,b<0,则直线l的方程为+=1.
由(1)知直线恒过定点(-1,-2),所以1=+≥2=2,得ab≥8,
当且仅当==,即a=-2,b=-4时等号成立,
所以S△AOB=ab≥×8=4,所以△AOB面积的最小值为4,此时直线的方程为1=+,即2x+y+4=0.
变式 (1)若直线l:ax+y-2-a=0在x轴和y轴上的截距相等,则直线l的斜率为 ( )
A.1 B.-1 C.-2或1 D.-1或2
[解析] (1)当直线ax+y-2-a=0过原点时,可得a=-2.
当直线ax+y-2-a=0不过原点时,由题意知a≠0,直线l在x轴上的截距为,
又直线l在y轴上的截距为2+a,所以=2+a,解得a=1或a=-2(舍).
综上,a=-2或1,所以直线l的斜率为-1或2.
D
(2)直线mx-y-3m+2=0(m∈R)必过点 ( )
A.(3,2) B.(-3,2) C.(-3,-2) D.(3,-2)
A
[解析] (2)由mx-y-3m+2=0,得m(x-3)-(y-2)=0,令x-3=0,y-2=0,可得x=3,y=2,所以直线必过点(3,2).
拓展 已知直线l:5ax-5y-a+3=0.
(1)求证:不论a为何值,直线l总经过第一象限;
(2)若直线l不经过第二象限,求a的取值范围.
解:(1)证明:方法一,将直线l的方程整理为y-=a (x-) ,所以直线l的斜率为a,且过定点A,) ,
而点A (,) 在第一象限内,故不论a为何值,直线l恒过第一象限.
方法二,直线l的方程可化为(5x-1)a-(5y-3)=0.令得即l过定点A (,) ,而点A (,) 在第一象限内,故不论a为何值,直线l恒过第一象限.
(2)如图所示,直线OA的斜率k==3,由图可知,要使l不经过第二象限,则需斜率a≥kOA=3,即a的取值范围为[3,+∞).
拓展 已知直线l:5ax-5y-a+3=0.
(1)求证:不论a为何值,直线l总经过第一象限;
(2)若直线l不经过第二象限,求a的取值范围.
第2章 直线和圆的方程
2.2.3 直线的一般式方程
思考:
(1)平面直角坐标系中任意一条直线都可以用一个关于x,y的二元一次方程表示吗?
(2)任意一个关于的二元一次方程都可以表示直线吗?
任意直线l经过点P0(x0,y0)
若直线l斜率不存在,即直线的倾斜角为90°时,直线的方程为=0
若直线l斜率存在,设直线的斜率为k,直线的方程为y-y0=k(x-x0).
关于x,y的二元一次方程
√
对于任意一个关于的二元一次方程
若,方程可变形为
若,方程可变形为
直线
√
1.关于x,y的二元一次方程都表示一条直线.我们把关于x,y的二元一次方程
(其中A,B不同时为0)叫作直线的 ,简称一般式.
知识点一 直线的一般式方程
Ax+By+C=0
一般式方程
2.直线的一般式方程与点斜式方程、斜截式方程、两点式方程、截距式方程之间互化:
y=-x-
+=1
思考:
在方程Ax+By+C=0中,系数A,B,C为何值时,表示的直线:
平行于x轴:
平行于y轴:
与x轴重合:
与y轴重合:
与x轴、y轴都相交:
过原点:
A=0,B ,C
A,B =0,C
A=0,B ,C
A,B =0,C
A·B≠0
C=0
知识点二 二元一次方程与直线
在平面直角坐标系中,任意一个二元一次方程是直角坐标平面上一条确定的直线;反之,直角坐标平面上的任意一条直线可以用一个确定的二元一次方程表示.
例:点集{(x,y)|x+y-1=0}表示的图形是直线x+y-1=0.
探究点一 求直线的一般式方程
例1 (1)直线2x-y-2=0绕它与y轴的交点A按逆时针方向旋转所得的直线的方程是 ( )
A.x-2y+4=0 B.x+2y-4=0 C.x-2y-4=0 D.x+2y+4=0
D
(2)根据下列各条件写出直线的方程,并化成一般式.
①斜率是-,且经过点A(8,-6)的直线的方程为 .
②经过点B(4,2),且平行于x轴的直线的方程为 .
③在x轴和y轴上的截距分别是和-3的直线的方程为 .
④经过点P1(3,-2),P2(5,-4)的直线的方程为 .
x+2y+4=0
y-2=0
2x-y-3=0
x+y-1=0
探究点二 含参数的直线一般式方程的有关问题
解:(1)当m+1=0,即m=-1时,直线l1的斜率k1不存在,直线l2的斜率k2=,两直线不平行;
当m+1≠0,即m≠-1时,将两直线方程化为斜截式,可得l1:y=-x-,l2:y=-x+.
由l1∥l2知两直线斜率相等,在y轴上的截距不相等,所以-=-,且-≠,
解得m=2或m=-3,符合题意。
综上所述,m的值为2或-3.
例2 (1)直线l1:2x+(m+1)y+4=0与直线l2:mx+3y-2=0平行,求m的值;
若l1∥l2 A1B2-A2B1=0且B1C2-B2C1≠0(或A1C2-A2C1≠0).
(2)直线l1:ax+(1-a)y-3=0与直线l2:(a-1)x+(2a+3)y-2=0垂直,求a的值.
解:(2)当a=1时,l1:x=3,l2:y=,所以l1⊥l2;
当a=-时,l1:y=x+,l2:x=-,所以l1不垂直于l2;
当a≠1且a≠-时,k1=,k2=,由于l1⊥l2,则·=-1,可得a=-3.
综上可知,当a=1或a=-3时,l1⊥l2.
若l1⊥l2 A1A2+B1B2=0.
[小结]
(1)直线l1:A1x+B1y+C1=0,直线l2:A2x+B2y+C2=0,
①若l1∥l2 A1B2-A2B1=0且B1C2-B2C1≠0(或A1C2-A2C1≠0).
②若l1⊥l2 A1A2+B1B2=0.
(2)与直线Ax+By+C=0平行的直线方程可设为 Ax+By+C1=0(C1≠C);
与直线Ax+By+C=0垂直的直线方程可设为Bx-Ay+C2=0.
解:(1)证明:直线方程(2-m)x+(2m+1)y+3m+4=0可化为(2x+y+4)+m(-x+2y+3)=0,
由题意知该方程对任意m都成立,
所以解得所以直线恒过定点(-1,-2).
例3 已知直线方程为(2-m)x+(2m+1)y+3m+4=0.
(1)证明:直线恒过定点;
(2)若直线分别与x轴、y轴的负半轴交于A,B两点,求△AOB面积的最小值及此时直线的方程.
例3 已知直线方程为(2-m)x+(2m+1)y+3m+4=0.
(1)证明:直线恒过定点;
(2)若直线分别与x轴、y轴的负半轴交于A,B两点,求△AOB面积的最小值及此时直线的方程.
(2)方法一:
由(1)知直线过定点(-1,-2),结合题意可设直线的方程为y+2=k(x+1),k<0,则A (-1,0) ,B(0,k-2),
所以S△AOB= |-1| |k-2|= (-1) (k-2)=2+ (+) ≥2+2=4,
当且仅当k=-2时取等号,所以△AOB面积的最小值为4,
此时直线的方程为2x+y+4=0.
例3 已知直线方程为(2-m)x+(2m+1)y+3m+4=0.
(1)证明:直线恒过定点;
(2)若直线分别与x轴、y轴的负半轴交于A,B两点,求△AOB面积的最小值及此时直线的方程.
方法二:
设A(a,0),B(0,b),显然a<0,b<0,则直线l的方程为+=1.
由(1)知直线恒过定点(-1,-2),所以1=+≥2=2,得ab≥8,
当且仅当==,即a=-2,b=-4时等号成立,
所以S△AOB=ab≥×8=4,所以△AOB面积的最小值为4,此时直线的方程为1=+,即2x+y+4=0.
变式 (1)若直线l:ax+y-2-a=0在x轴和y轴上的截距相等,则直线l的斜率为 ( )
A.1 B.-1 C.-2或1 D.-1或2
[解析] (1)当直线ax+y-2-a=0过原点时,可得a=-2.
当直线ax+y-2-a=0不过原点时,由题意知a≠0,直线l在x轴上的截距为,
又直线l在y轴上的截距为2+a,所以=2+a,解得a=1或a=-2(舍).
综上,a=-2或1,所以直线l的斜率为-1或2.
D
(2)直线mx-y-3m+2=0(m∈R)必过点 ( )
A.(3,2) B.(-3,2) C.(-3,-2) D.(3,-2)
A
[解析] (2)由mx-y-3m+2=0,得m(x-3)-(y-2)=0,令x-3=0,y-2=0,可得x=3,y=2,所以直线必过点(3,2).
拓展 已知直线l:5ax-5y-a+3=0.
(1)求证:不论a为何值,直线l总经过第一象限;
(2)若直线l不经过第二象限,求a的取值范围.
解:(1)证明:方法一,将直线l的方程整理为y-=a (x-) ,所以直线l的斜率为a,且过定点A,) ,
而点A (,) 在第一象限内,故不论a为何值,直线l恒过第一象限.
方法二,直线l的方程可化为(5x-1)a-(5y-3)=0.令得即l过定点A (,) ,而点A (,) 在第一象限内,故不论a为何值,直线l恒过第一象限.
(2)如图所示,直线OA的斜率k==3,由图可知,要使l不经过第二象限,则需斜率a≥kOA=3,即a的取值范围为[3,+∞).
拓展 已知直线l:5ax-5y-a+3=0.
(1)求证:不论a为何值,直线l总经过第一象限;
(2)若直线l不经过第二象限,求a的取值范围.
