12.2 三角形全等的判定(2)学案
文档属性
| 名称 | 12.2 三角形全等的判定(2)学案 |  | |
| 格式 | zip | ||
| 文件大小 | 47.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-09-12 21:17:03 | ||
图片预览


文档简介
2013学年初二数学新人教版八年级上册12.2三角形全等的判定(2)学案
【学习目标】:
1.理解三角形全等的判定定理“边角边”;
2.会运用“SAS”识别三角形全等,为证明线段相等或角相等创造条件;
3.经历探索三角形全等条件的过程,体会利用操作、归纳获得数学结论的过程.
【学习重点】:用SAS的方法证明两个三角形全等及证明三角形全等时的书写格式.
【学习难点】:1、探索两个三角形全等的判定方法SAS;
2、用SAS的方法证明两个三角形全等,进而证明角相等、线段相等与平行.
【课前自学、课中交流】
一、创设情境
1.判定两个三角形全等的方法有什么? .
2.我们已经知道两个三角形只满足一个或两个相等的条件不能保证两个三角形全等,对于满足三个条件我们已经讨论了SSS可以全等,那么其它情况呢?
3. 满足三个条件
本节课我们一起来探究两边及一角对应相等的情况.
二、自主探究
(一)探索三角形全等的条件
1.如图1,AC、BD相交于O,AO、BO、CO、DO的长度如图所标,△ABO和△CDO是否能完全重合呢?为什么?
(1)在上面的例子中我们已知哪些条件(从三角形的边、角关系作答),得到什么结论?AO= ,BO= ,∠AOB=∠ .
(2)由(1)中的回答,你能得到什么猜想?
图1
2.上述猜想是否正确呢?不妨按上述条件画图并作如下的实验:
(1)读句画图:
①画∠DAE=45°,
②在AD、AE上分别取 B、C,使 AB=3.5cm, AC=2.5cm.
③连结BC,得△ABC.
④按上述画法再画一个△A'B'C'.使A'B'=AB, A'C'=AC,∠A'=∠A。
(2)把△A'B'C'剪下来放到△ABC上,观察△A'B'C'与△ABC是否能够完全重合?
归纳总结: 相等的两个三角形全等(简称“边角边”或“SAS”)
巩固练习一:如图2,已知AD∥BC,AD=CB.求证:△ABC≌△CDA.
(提示:要证明两个三角形全等,已具有两个条件,一是
AD=CB(已知),二是___________,三是___________,
证明:∵AD∥BC, 图2
∴∠DAC=_______.
在△ADC与△ABC中,
∴ △ABC≌△CDA.
(二)探究:如果“两边及其中一边的对角对应相等,那么这两个三角形全等吗?”
画一画:三角形的两条边分别为4cm和3cm,长度为3cm的边所对的角为30度,画出这个三角形,把你画的三角形与其他同学画的三角形进行比较,由此你发现了什么?把你的发现和同伴交流。
知识点归纳:三角形全等判定条件(2) 。
【当堂训练】
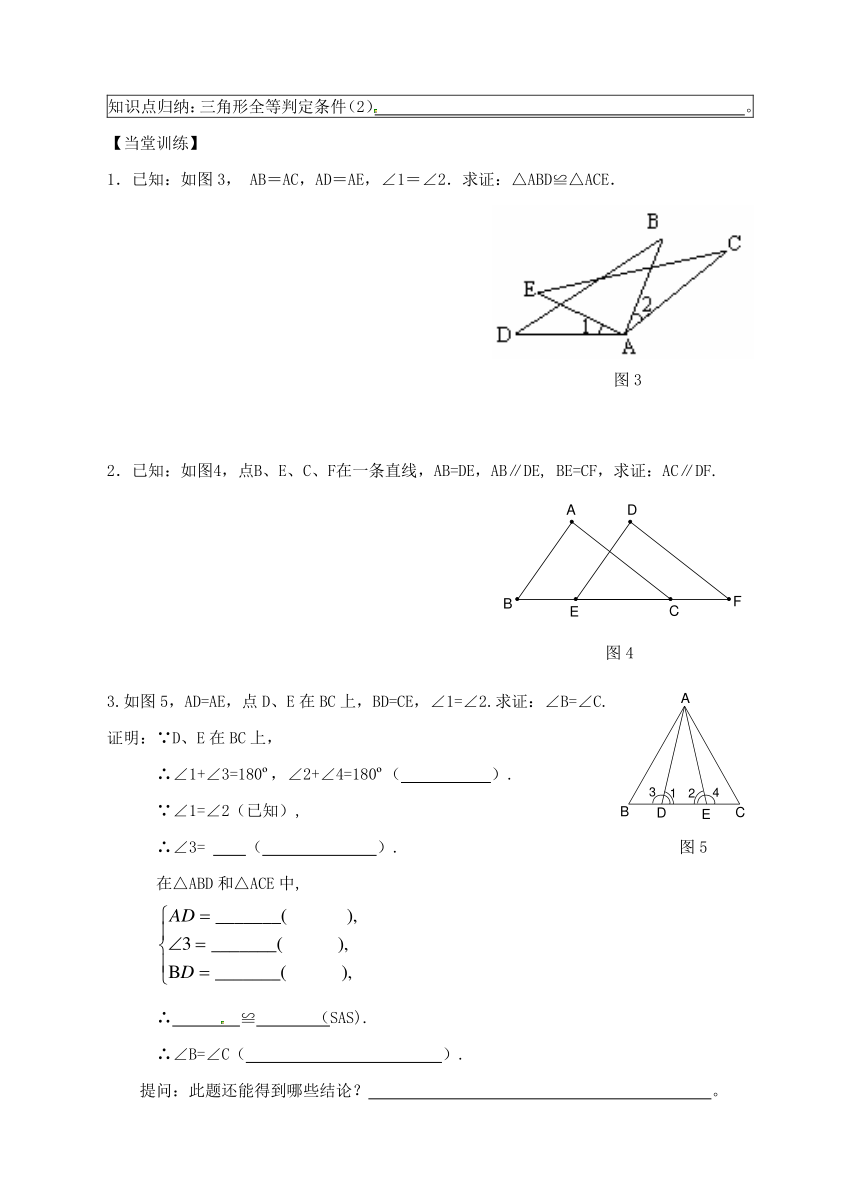
1.已知:如图3, AB=AC,AD=AE,∠1=∠2.求证:△ABD≌△ACE.
图3
2.已知:如图4,点B、E、C、F在一条直线,AB=DE,AB∥DE, BE=CF,求证:AC∥DF.
图4
3.如图5,AD=AE,点D、E在BC上,BD=CE,∠1=∠2.求证:∠B=∠C.
证明:∵D、E在BC上,
∴∠1+∠3=180 ,∠2+∠4=180 ( ).
∵∠1=∠2(已知),
∴∠3= ( ). 图5
在△ABD和△ACE中,
∴ ≌ (SAS).
∴∠B=∠C( ).
提问:此题还能得到哪些结论? 。
4.如图6,OA=OC,OB=OD,则图中有多少对全等三角形( )
A.2 B.3 C.4 D.5
图6 图7 图8 图9
5.如图7,AB=AC,AD=AE,欲证△ABD≌△ACE,可补充条件( )
A.∠1=∠2 B.∠B=∠C C.∠D=∠E D.∠BAE=∠CAD
6.如图8,AD=BC,要得到△ABD和△CDB全等,可以添加的条件是( )
A.AB∥CD B.AD∥BC C.∠A=∠C D.∠ABC=∠CDA
7.如图9,AB与CD交于点O,OA=OC,OD=OB,∠AOD=________,根据__________可得到△AOD≌△COB,从而可以得到AD=_________.
8.已知:如图10,△ABC中,AB=AC,AD平分∠BAC,请补充完整过程说明△ABD≌△ACD的理由.
证明:∵AD平分∠BAC,
∴∠________=∠_________(角平分线的定义).
在△ABD和△ACD中,
∵___________________________________________,
∴△ABD≌△ACD( ). 图10
9.已知:如图11, AB=AD,AC=AE,∠1=∠2,求证∠ADE=∠B.
图11
10.已知:如图12,AB=AD,若AC平分∠BAD,问AC是否平分∠BCD?为什么?
图12
11.已知:如图13(1),AB⊥BD,DE⊥BD,点C是BD上一点,且BC=DE,CD=AB.
(1)试判断AC与CE的关系,并说明理由.
(2)如图13(2),若把△CDE沿直线BD向左平移,使△CDE的顶点C与B重合,此时第(1)问中AC与BE的关系还成立吗?如果成立,请证明;如果不成立,请说明理由.
图13
【当堂训练】答案
1. 证明:∵∠1=∠2,
∴∠DAB=∠EAC.
在△ABD与△ACE中,
∴ △ABD≌△ACE(SAS).
2. 证明:∵AB∥DE,
∴∠ABC=∠DEF.
∵BE=CF,
∴BC=EF.
在△ABC与△DEF中,
∴ △ABC≌△DEF(SAS).
∴∠ACB=∠F.
∴AC∥DF.
3. 依次填:邻补角定义;∠4;等角的补角相等;AE;已知;∠4;已证;CE;已知;△ABD;△ACE;全等三角形的对应角相等.
4. C.
5. A.
6. C.
7. 依次填:∠COB;SAS;BC.
8. 依次填:∠BAD=∠CAD;AB=AC,∠BAD=∠CAD,AD=AD;SAS.
9. 证明:∵∠1=∠2,
∴∠CAB=∠EAD.
在△ABC与△ADE中,
∴ △ABC≌△ADE(SAS).
10. AC平分∠BCD.
证明:∵AC平分∠BAD,
∴∠CAB=∠CAD.
在△ABC与△ADC中,
∴ △ABC≌△ADC(SAS).
∴∠ACB=∠ACD,
即AC平分∠BCD.
11. (1)AC=CE, AC⊥CE.
证明:∵AB⊥BD,DE⊥BD,
∴∠ABC=∠CDE=90°.
在△ABC与△CDE中,
∴ △ABC≌△CDE(SAS).
∴AC=CE,∠A=∠ECD.
∵∠A+∠ACB=90°,
∴∠ECD+∠ACB=90°,
∴∠ACE=90°,
∴AC⊥CE.
(2)AC=BE, AC⊥BE.成立.
证明:设AC、BE交于点O.
∵AB⊥BD,DE⊥BD,
∴∠ABC=∠CDE=90°.
在△ABC与△BDE中,
∴ △ABC≌△BDE(SAS).
∴AC=BE,∠A=∠EBD.
∵∠A+∠ACB=90°,
∴∠EBD+∠ACB=90°,
∴∠BOC=90°,
∴AC⊥BE.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
【学习目标】:
1.理解三角形全等的判定定理“边角边”;
2.会运用“SAS”识别三角形全等,为证明线段相等或角相等创造条件;
3.经历探索三角形全等条件的过程,体会利用操作、归纳获得数学结论的过程.
【学习重点】:用SAS的方法证明两个三角形全等及证明三角形全等时的书写格式.
【学习难点】:1、探索两个三角形全等的判定方法SAS;
2、用SAS的方法证明两个三角形全等,进而证明角相等、线段相等与平行.
【课前自学、课中交流】
一、创设情境
1.判定两个三角形全等的方法有什么? .
2.我们已经知道两个三角形只满足一个或两个相等的条件不能保证两个三角形全等,对于满足三个条件我们已经讨论了SSS可以全等,那么其它情况呢?
3. 满足三个条件
本节课我们一起来探究两边及一角对应相等的情况.
二、自主探究
(一)探索三角形全等的条件
1.如图1,AC、BD相交于O,AO、BO、CO、DO的长度如图所标,△ABO和△CDO是否能完全重合呢?为什么?
(1)在上面的例子中我们已知哪些条件(从三角形的边、角关系作答),得到什么结论?AO= ,BO= ,∠AOB=∠ .
(2)由(1)中的回答,你能得到什么猜想?
图1
2.上述猜想是否正确呢?不妨按上述条件画图并作如下的实验:
(1)读句画图:
①画∠DAE=45°,
②在AD、AE上分别取 B、C,使 AB=3.5cm, AC=2.5cm.
③连结BC,得△ABC.
④按上述画法再画一个△A'B'C'.使A'B'=AB, A'C'=AC,∠A'=∠A。
(2)把△A'B'C'剪下来放到△ABC上,观察△A'B'C'与△ABC是否能够完全重合?
归纳总结: 相等的两个三角形全等(简称“边角边”或“SAS”)
巩固练习一:如图2,已知AD∥BC,AD=CB.求证:△ABC≌△CDA.
(提示:要证明两个三角形全等,已具有两个条件,一是
AD=CB(已知),二是___________,三是___________,
证明:∵AD∥BC, 图2
∴∠DAC=_______.
在△ADC与△ABC中,
∴ △ABC≌△CDA.
(二)探究:如果“两边及其中一边的对角对应相等,那么这两个三角形全等吗?”
画一画:三角形的两条边分别为4cm和3cm,长度为3cm的边所对的角为30度,画出这个三角形,把你画的三角形与其他同学画的三角形进行比较,由此你发现了什么?把你的发现和同伴交流。
知识点归纳:三角形全等判定条件(2) 。
【当堂训练】
1.已知:如图3, AB=AC,AD=AE,∠1=∠2.求证:△ABD≌△ACE.
图3
2.已知:如图4,点B、E、C、F在一条直线,AB=DE,AB∥DE, BE=CF,求证:AC∥DF.
图4
3.如图5,AD=AE,点D、E在BC上,BD=CE,∠1=∠2.求证:∠B=∠C.
证明:∵D、E在BC上,
∴∠1+∠3=180 ,∠2+∠4=180 ( ).
∵∠1=∠2(已知),
∴∠3= ( ). 图5
在△ABD和△ACE中,
∴ ≌ (SAS).
∴∠B=∠C( ).
提问:此题还能得到哪些结论? 。
4.如图6,OA=OC,OB=OD,则图中有多少对全等三角形( )
A.2 B.3 C.4 D.5
图6 图7 图8 图9
5.如图7,AB=AC,AD=AE,欲证△ABD≌△ACE,可补充条件( )
A.∠1=∠2 B.∠B=∠C C.∠D=∠E D.∠BAE=∠CAD
6.如图8,AD=BC,要得到△ABD和△CDB全等,可以添加的条件是( )
A.AB∥CD B.AD∥BC C.∠A=∠C D.∠ABC=∠CDA
7.如图9,AB与CD交于点O,OA=OC,OD=OB,∠AOD=________,根据__________可得到△AOD≌△COB,从而可以得到AD=_________.
8.已知:如图10,△ABC中,AB=AC,AD平分∠BAC,请补充完整过程说明△ABD≌△ACD的理由.
证明:∵AD平分∠BAC,
∴∠________=∠_________(角平分线的定义).
在△ABD和△ACD中,
∵___________________________________________,
∴△ABD≌△ACD( ). 图10
9.已知:如图11, AB=AD,AC=AE,∠1=∠2,求证∠ADE=∠B.
图11
10.已知:如图12,AB=AD,若AC平分∠BAD,问AC是否平分∠BCD?为什么?
图12
11.已知:如图13(1),AB⊥BD,DE⊥BD,点C是BD上一点,且BC=DE,CD=AB.
(1)试判断AC与CE的关系,并说明理由.
(2)如图13(2),若把△CDE沿直线BD向左平移,使△CDE的顶点C与B重合,此时第(1)问中AC与BE的关系还成立吗?如果成立,请证明;如果不成立,请说明理由.
图13
【当堂训练】答案
1. 证明:∵∠1=∠2,
∴∠DAB=∠EAC.
在△ABD与△ACE中,
∴ △ABD≌△ACE(SAS).
2. 证明:∵AB∥DE,
∴∠ABC=∠DEF.
∵BE=CF,
∴BC=EF.
在△ABC与△DEF中,
∴ △ABC≌△DEF(SAS).
∴∠ACB=∠F.
∴AC∥DF.
3. 依次填:邻补角定义;∠4;等角的补角相等;AE;已知;∠4;已证;CE;已知;△ABD;△ACE;全等三角形的对应角相等.
4. C.
5. A.
6. C.
7. 依次填:∠COB;SAS;BC.
8. 依次填:∠BAD=∠CAD;AB=AC,∠BAD=∠CAD,AD=AD;SAS.
9. 证明:∵∠1=∠2,
∴∠CAB=∠EAD.
在△ABC与△ADE中,
∴ △ABC≌△ADE(SAS).
10. AC平分∠BCD.
证明:∵AC平分∠BAD,
∴∠CAB=∠CAD.
在△ABC与△ADC中,
∴ △ABC≌△ADC(SAS).
∴∠ACB=∠ACD,
即AC平分∠BCD.
11. (1)AC=CE, AC⊥CE.
证明:∵AB⊥BD,DE⊥BD,
∴∠ABC=∠CDE=90°.
在△ABC与△CDE中,
∴ △ABC≌△CDE(SAS).
∴AC=CE,∠A=∠ECD.
∵∠A+∠ACB=90°,
∴∠ECD+∠ACB=90°,
∴∠ACE=90°,
∴AC⊥CE.
(2)AC=BE, AC⊥BE.成立.
证明:设AC、BE交于点O.
∵AB⊥BD,DE⊥BD,
∴∠ABC=∠CDE=90°.
在△ABC与△BDE中,
∴ △ABC≌△BDE(SAS).
∴AC=BE,∠A=∠EBD.
∵∠A+∠ACB=90°,
∴∠EBD+∠ACB=90°,
∴∠BOC=90°,
∴AC⊥BE.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
