数学人教A版(2019)选择性必修第一册2.1.1 倾斜角和斜率 课件(共21张ppt)
文档属性
| 名称 | 数学人教A版(2019)选择性必修第一册2.1.1 倾斜角和斜率 课件(共21张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-17 09:18:06 | ||
图片预览








文档简介
(共21张PPT)
第2章 直线和圆的方程
2.1.1 倾斜角与斜率
设A、B为直线上的两点,则就是这条直线的方向向量.
一个点和一个方向确定一条直线。
问题1:我们知道,两点可以确定一条直线,那如果已知一点,可以确定直线吗?
还需附加什么条件,才能确定直线?
不能确定.附加另一个点或附加一个方向.
问题2:如图, 过一点P可以作无数多条直线a,b,c, …,这些直线有什么联系呢
(1)它们都经过点P. (2)它们的“倾斜程度”不同.
问题3:那么怎样描述这种“倾斜程度”的不同
直线与x轴所成的角不同.
1.定义:当直线l与x轴相交时,我们以x轴为基准,x轴正向与直线l 的方向之间所成的角α叫作直线l的倾斜角.
特别地,当 时,我们规定它的倾斜角为0°.
2.倾斜角α的取值范围: .
向上
直线l与x轴平行或重合
0°≤α<180°
零度角
锐角
直角
钝角
3.按倾斜角去分类,直线可分几类?
1、所有的直线都有唯一确定的倾斜角与它对应。
2、每一个倾斜角都对应于唯一的一条直线。
由两点确定一条直线可知,直线l由点唯一确定.
所以,直线l的倾斜角一定与的坐标有内在联系.
下面我们进一步研究刻画直线倾斜程度的方法.
探究:在平面直角坐标系中,设直线l的倾斜角为α
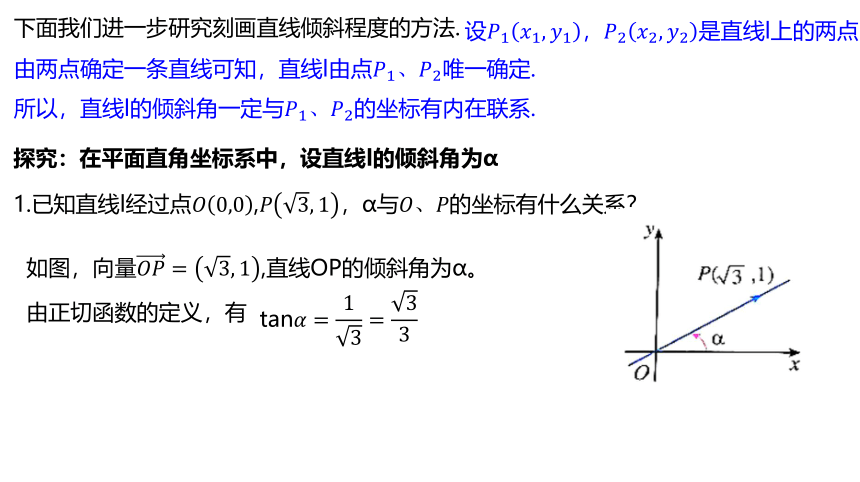
1.已知直线l经过点,,α与的坐标有什么关系?
设,是直线l上的两点.
如图,向量,直线OP的倾斜角为α。
由正切函数的定义,有
由两点确定一条直线可知,直线l由点唯一确定.
所以,直线l的倾斜角一定与的坐标有内在联系.
下面我们进一步研究刻画直线倾斜程度的方法.
探究:在平面直角坐标系中,设直线l的倾斜角为α
2.已知直线l经过点,,α与的坐标又有什么关系?
设,是直线l上的两点.
如图,向量,平移向量
则点P的坐标为,且直线OP的倾斜角为α
由正切函数的定义,有
由两点确定一条直线可知,直线l由点唯一确定.
所以,直线l的倾斜角一定与的坐标有内在联系.
下面我们进一步研究刻画直线倾斜程度的方法.
探究:在平面直角坐标系中,设直线l的倾斜角为α
3.已知直线l经过点,,α与的坐标又有什么关系?
设,是直线l上的两点.
一般地,如图,当向量的方向向上时,。
平移向量,则点,且直线OP的倾斜角也为α。
由正切函数的定义,有
同样当向量的方向向上时,
tanα=
思考:当直线l与坐标轴平行或重合时,上述式子还成立吗?
当直线的倾斜角是锐角时,
“坡度(比)”是“倾斜角的正切值”
水平宽度
铅直高度
日常生活中,常常用“坡度(坡比)”表示倾斜面的倾斜程度:
问题5:“坡度”对照“倾斜角,两者有什么关系?
倾斜角是90°的直线没有斜率。
描述直线倾斜程度的量——直线的斜率
①倾斜角不同的直线斜率也不同.
②任何一条直线都有倾斜角,但不一定有斜率.
③倾斜角互补,斜率互为相反数.
o
k
1.定义:直线P1P2上的向量以及与它 的非零向量都是直线P1P2的 .
2.若P1(x1,y1),P2(x2,y2)是直线P1P2上的两点,则直线P1P2的一个方向向量= .
平行
方向向量
(x2-x1,y2-y1)
3.直线的方向向量与斜率的关系
(1)经过两点P1(x1,y1),P2(x2,y2)(x1≠x2)的直线,
其方向向量为=(x2-x1,y2-y1)=(x2-x1) (1,) ,
因此,当直线的斜率k存在时,直线的一个方向向量为 ;
(2)若直线的一个方向向量为(x,y)(x≠0),则直线的斜率k= .
(1,k)
(3)当直线的斜率不存在时,直线的方向向量与向量(0,1)共线.
探究点一 直线的倾斜角问题
例1 (1)如图 (1)和(2),直线l1和l2的倾斜角分别是 ( )
(2)若过点P(1,1+a)和Q(3,2a)的直线的倾斜角α为钝角,求实数a的取值范围.
解:由题意知直线PQ的斜率k=tan α=<0,所以a<1,故实数a的取值范围是a<1.
(3)已知直线l的倾斜角α=45°,且P1(2,y1),P2(x2,5),P3(3,1)是直线l上的三点,求x2,y1的值.
探究点一 直线的倾斜角问题
(3)已知直线l的倾斜角α=45°,且P1(2,y1),P2(x2,5),P3(3,1)是直线l上的三点,求x2,y1的值.
解: ∵α=45°,∴直线l的斜率k=tan 45°=1,
又P1,P2,P3都在直线l上,∴==k,即==1,解得x2=7,y1=0.
斜率公式的应用1:三点共线的证明
变式 (1)一条直线l与x轴相交,其向上的方向与x轴的负方向所成的角为α,则l的倾斜角为( )
A.α B.180°-α C.90°+α D.90°+α或90°-α
[解析] (1) 当α为锐角时,l的倾斜角为180°-α;
当α为钝角时,l的倾斜角为180°-α;
当α为90°时,l的倾斜角为90°.故选B.
B
(2)直线l1⊥l2,若直线l1的倾斜角为α,直线l2的倾斜角为β(β>α),则下列说法正确的是 ( )
A.β-α=90° B.α+β=90° C.α+β=180° D.β-α为锐角
[解析] (2)由题意,作出图形如图,则β=90°+α,所以β-α=90°.故选A.
A
拓展 已知两点A(-3,4),B(3,2),过点P(1,0)的直线l与线段AB有公共点,则直线l的斜率k的取值范围是 ,直线l的倾斜角α的取值范围是 .
[解析] 如图所示,由题意可知kPA==-1,kPB==1.
要使直线l与线段AB有公共点,则直线l的斜率k的取值范围是k≤-1或k≥1.
由题意可知,直线l的倾斜角α大于等于直线PB的倾斜角,小于等于直线PA的倾斜角,
又PB的倾斜角是45°,PA的倾斜角是135°,所以α的取值范围是45°≤α≤135°.
k≤-1或k≥1
45°≤α≤135°
探究点二 求直线的斜率问题
[解析] (1)如图所示,当直线l在l1位置时,直线l的斜率k=tan 0°=0;
当直线l在l2位置时,直线l的斜率k==2.
故直线l的斜率的取值范围是[0,2].
例2(1)直线l过点A(1,2),且不过第四象限,则直线l的斜率的取值范围是 ( )
A.[0,2] B.[0,1] C. D.
A
(2)已知直线l1的方向向量为n=(2,1),直线l2倾斜角是直线l1倾斜角的2倍,求直线l2的斜率.
解:设直线l1的倾斜角为α(0°≤α<90°).由直线l1的方向向量为n=(2,1),得直线l1的斜率k1=tan α=,
因此直线l2的斜率k2=tan 2α==.
拓展若点P(x,y)在以A(2,4),B(3,2)为端点的线段上,求的最大值和最小值.
解:如图所示,连接OA,OB,OP.
由于的几何意义是直线OP的斜率,且kOA=2,kOB=,所以可得的最大值为2,最小值为.
斜率公式的应用2:利用斜率公式构造斜率,灵活解决形如之类的问题
练已知实数x,y满足y=x2-x+2(-1≤x≤1),试求的最大值和最小值.
解:的几何意义表示经过点P(-2,-3)与曲线y=x2-x+2(-1≤x≤1)上任意一点(x,y)的直线的斜率k.
在平面直角坐标系中作出点P与对应的曲线,记该曲线的两个端点为A,B,并连接PA,PB,如图所示.
由图可知kPA≤k≤kPB,由已知可得A(1,2),B(-1,4),
则kPA==,kPB==7,
所以≤k≤7,
所以的最大值为7,最小值为.
拓展
探究点三 直线的方向向量的应用
[解析] (1)依题意得=(2,2),由与方向向量(1,k)共线,可得2k-2=0,因此k=1.
例3 (1)已知经过两点A(2,3),B(4,5)的直线的一个方向向量为(1,k),则k的值为 .
1
(2)已知直线l的一个方向向量为(2,4),则直线l的斜率为 .
[解析] (2)因为直线l的一个方向向量为(2,4),所以直线l的斜率k==2.
2
(3)若三点A(2,1),B(-2,m),C(6,8)都在直线l上,则实数m的值为 .
[解析] (3)依题意得=(-4,m-1),=(4,7),由这两个向量都是直线l的方向向量得∥,
因此4(m-1)-(-4)×7=0,∴m=-6.
-6
第2章 直线和圆的方程
2.1.1 倾斜角与斜率
设A、B为直线上的两点,则就是这条直线的方向向量.
一个点和一个方向确定一条直线。
问题1:我们知道,两点可以确定一条直线,那如果已知一点,可以确定直线吗?
还需附加什么条件,才能确定直线?
不能确定.附加另一个点或附加一个方向.
问题2:如图, 过一点P可以作无数多条直线a,b,c, …,这些直线有什么联系呢
(1)它们都经过点P. (2)它们的“倾斜程度”不同.
问题3:那么怎样描述这种“倾斜程度”的不同
直线与x轴所成的角不同.
1.定义:当直线l与x轴相交时,我们以x轴为基准,x轴正向与直线l 的方向之间所成的角α叫作直线l的倾斜角.
特别地,当 时,我们规定它的倾斜角为0°.
2.倾斜角α的取值范围: .
向上
直线l与x轴平行或重合
0°≤α<180°
零度角
锐角
直角
钝角
3.按倾斜角去分类,直线可分几类?
1、所有的直线都有唯一确定的倾斜角与它对应。
2、每一个倾斜角都对应于唯一的一条直线。
由两点确定一条直线可知,直线l由点唯一确定.
所以,直线l的倾斜角一定与的坐标有内在联系.
下面我们进一步研究刻画直线倾斜程度的方法.
探究:在平面直角坐标系中,设直线l的倾斜角为α
1.已知直线l经过点,,α与的坐标有什么关系?
设,是直线l上的两点.
如图,向量,直线OP的倾斜角为α。
由正切函数的定义,有
由两点确定一条直线可知,直线l由点唯一确定.
所以,直线l的倾斜角一定与的坐标有内在联系.
下面我们进一步研究刻画直线倾斜程度的方法.
探究:在平面直角坐标系中,设直线l的倾斜角为α
2.已知直线l经过点,,α与的坐标又有什么关系?
设,是直线l上的两点.
如图,向量,平移向量
则点P的坐标为,且直线OP的倾斜角为α
由正切函数的定义,有
由两点确定一条直线可知,直线l由点唯一确定.
所以,直线l的倾斜角一定与的坐标有内在联系.
下面我们进一步研究刻画直线倾斜程度的方法.
探究:在平面直角坐标系中,设直线l的倾斜角为α
3.已知直线l经过点,,α与的坐标又有什么关系?
设,是直线l上的两点.
一般地,如图,当向量的方向向上时,。
平移向量,则点,且直线OP的倾斜角也为α。
由正切函数的定义,有
同样当向量的方向向上时,
tanα=
思考:当直线l与坐标轴平行或重合时,上述式子还成立吗?
当直线的倾斜角是锐角时,
“坡度(比)”是“倾斜角的正切值”
水平宽度
铅直高度
日常生活中,常常用“坡度(坡比)”表示倾斜面的倾斜程度:
问题5:“坡度”对照“倾斜角,两者有什么关系?
倾斜角是90°的直线没有斜率。
描述直线倾斜程度的量——直线的斜率
①倾斜角不同的直线斜率也不同.
②任何一条直线都有倾斜角,但不一定有斜率.
③倾斜角互补,斜率互为相反数.
o
k
1.定义:直线P1P2上的向量以及与它 的非零向量都是直线P1P2的 .
2.若P1(x1,y1),P2(x2,y2)是直线P1P2上的两点,则直线P1P2的一个方向向量= .
平行
方向向量
(x2-x1,y2-y1)
3.直线的方向向量与斜率的关系
(1)经过两点P1(x1,y1),P2(x2,y2)(x1≠x2)的直线,
其方向向量为=(x2-x1,y2-y1)=(x2-x1) (1,) ,
因此,当直线的斜率k存在时,直线的一个方向向量为 ;
(2)若直线的一个方向向量为(x,y)(x≠0),则直线的斜率k= .
(1,k)
(3)当直线的斜率不存在时,直线的方向向量与向量(0,1)共线.
探究点一 直线的倾斜角问题
例1 (1)如图 (1)和(2),直线l1和l2的倾斜角分别是 ( )
(2)若过点P(1,1+a)和Q(3,2a)的直线的倾斜角α为钝角,求实数a的取值范围.
解:由题意知直线PQ的斜率k=tan α=<0,所以a<1,故实数a的取值范围是a<1.
(3)已知直线l的倾斜角α=45°,且P1(2,y1),P2(x2,5),P3(3,1)是直线l上的三点,求x2,y1的值.
探究点一 直线的倾斜角问题
(3)已知直线l的倾斜角α=45°,且P1(2,y1),P2(x2,5),P3(3,1)是直线l上的三点,求x2,y1的值.
解: ∵α=45°,∴直线l的斜率k=tan 45°=1,
又P1,P2,P3都在直线l上,∴==k,即==1,解得x2=7,y1=0.
斜率公式的应用1:三点共线的证明
变式 (1)一条直线l与x轴相交,其向上的方向与x轴的负方向所成的角为α,则l的倾斜角为( )
A.α B.180°-α C.90°+α D.90°+α或90°-α
[解析] (1) 当α为锐角时,l的倾斜角为180°-α;
当α为钝角时,l的倾斜角为180°-α;
当α为90°时,l的倾斜角为90°.故选B.
B
(2)直线l1⊥l2,若直线l1的倾斜角为α,直线l2的倾斜角为β(β>α),则下列说法正确的是 ( )
A.β-α=90° B.α+β=90° C.α+β=180° D.β-α为锐角
[解析] (2)由题意,作出图形如图,则β=90°+α,所以β-α=90°.故选A.
A
拓展 已知两点A(-3,4),B(3,2),过点P(1,0)的直线l与线段AB有公共点,则直线l的斜率k的取值范围是 ,直线l的倾斜角α的取值范围是 .
[解析] 如图所示,由题意可知kPA==-1,kPB==1.
要使直线l与线段AB有公共点,则直线l的斜率k的取值范围是k≤-1或k≥1.
由题意可知,直线l的倾斜角α大于等于直线PB的倾斜角,小于等于直线PA的倾斜角,
又PB的倾斜角是45°,PA的倾斜角是135°,所以α的取值范围是45°≤α≤135°.
k≤-1或k≥1
45°≤α≤135°
探究点二 求直线的斜率问题
[解析] (1)如图所示,当直线l在l1位置时,直线l的斜率k=tan 0°=0;
当直线l在l2位置时,直线l的斜率k==2.
故直线l的斜率的取值范围是[0,2].
例2(1)直线l过点A(1,2),且不过第四象限,则直线l的斜率的取值范围是 ( )
A.[0,2] B.[0,1] C. D.
A
(2)已知直线l1的方向向量为n=(2,1),直线l2倾斜角是直线l1倾斜角的2倍,求直线l2的斜率.
解:设直线l1的倾斜角为α(0°≤α<90°).由直线l1的方向向量为n=(2,1),得直线l1的斜率k1=tan α=,
因此直线l2的斜率k2=tan 2α==.
拓展若点P(x,y)在以A(2,4),B(3,2)为端点的线段上,求的最大值和最小值.
解:如图所示,连接OA,OB,OP.
由于的几何意义是直线OP的斜率,且kOA=2,kOB=,所以可得的最大值为2,最小值为.
斜率公式的应用2:利用斜率公式构造斜率,灵活解决形如之类的问题
练已知实数x,y满足y=x2-x+2(-1≤x≤1),试求的最大值和最小值.
解:的几何意义表示经过点P(-2,-3)与曲线y=x2-x+2(-1≤x≤1)上任意一点(x,y)的直线的斜率k.
在平面直角坐标系中作出点P与对应的曲线,记该曲线的两个端点为A,B,并连接PA,PB,如图所示.
由图可知kPA≤k≤kPB,由已知可得A(1,2),B(-1,4),
则kPA==,kPB==7,
所以≤k≤7,
所以的最大值为7,最小值为.
拓展
探究点三 直线的方向向量的应用
[解析] (1)依题意得=(2,2),由与方向向量(1,k)共线,可得2k-2=0,因此k=1.
例3 (1)已知经过两点A(2,3),B(4,5)的直线的一个方向向量为(1,k),则k的值为 .
1
(2)已知直线l的一个方向向量为(2,4),则直线l的斜率为 .
[解析] (2)因为直线l的一个方向向量为(2,4),所以直线l的斜率k==2.
2
(3)若三点A(2,1),B(-2,m),C(6,8)都在直线l上,则实数m的值为 .
[解析] (3)依题意得=(-4,m-1),=(4,7),由这两个向量都是直线l的方向向量得∥,
因此4(m-1)-(-4)×7=0,∴m=-6.
-6
