1.3 集合的基本运算(含2课时) 课件(共23张PPT)
文档属性
| 名称 | 1.3 集合的基本运算(含2课时) 课件(共23张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-17 11:15:12 | ||
图片预览







文档简介
(共23张PPT)
第一章 《集合与常用逻辑用语》
1.3 集合的基本运算(1)
实数间的大小关系
类比
集合间的包含关系
实数间的基本运算
类比
集合间的基本运算
加法运算
“相加”
观察下列各个集合,你能说出集合C与集合A,B之间的关系吗?
(1)A={1,3,5},B={2,4,6},C={1,2,3,4,5,6};
(2)A={x|x是有理数},B={x|x是无理数},C={x|x是实数};
(3)A={1,2,3},B={2,3,5,9},C={1,2,3,5,9}
C是由所有属于集合A或属于集合B的元素组成的.
类比实数的加法运算,你能否尝试定义集合间 “相加”运算?
课前思考
1∈A
5∈B
2∈A
且1∈B
且5∈A
且2∈B
称C是A和B的并集
只属于A
只属于B
属于A且属于B
1.1定义:由所有属于集合A或属于集合B的元素组成的集合,
叫做A和B的并集,记作A∪B,读作A并B。
新知1.并集
1.2符号语言:
A∪B={x|x∈A,或x∈B}
1.3图形语言:
A={1,3,5}, B={2,4,6}
A∪B={1,3,5,2,4,6}
A={1,3}, B={2,3,5}
A∪B={1,2,3,5}
A={1,3}, B={1,3,5}
A∪B={1,3,5}
1.4性质:
①A∪A=A;
⑤A∪B=B
A B;
[注]或的3个含义:①x∈A但x∈B;②x∈B但x∈A;③x∈A且x∈B
④A (A∪B);B (A∪B);
②A∪ =A;
③A∪B=B∪A
新知1.并集
【例2】设集合A={x|-2{2,3,5,6,7,8}
A∪B={x|x<2}
公共元素在并集中只能出现一次(互异性)
看数轴
【例1】设A={2,3,6,8},B={3,5,7,8},则A∪B=________________.
【变式1】集合A={x|-2A B
{a|a≥2}
【变式2】集合A={x|x<1或x>3}, B={x|x{a|a>3}
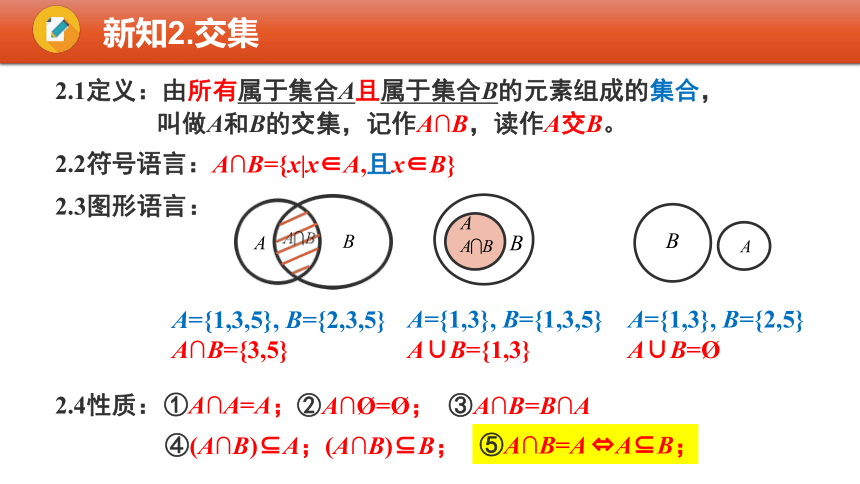
2.1定义:由所有属于集合A且属于集合B的元素组成的集合,
叫做A和B的交集,记作A∩B,读作A交B。
新知2.交集
2.2符号语言:
A∩B={x|x∈A,且x∈B}
2.3图形语言:
A={1,3,5}, B={2,3,5}
A∩B={3,5}
A={1,3}, B={1,3,5}
A∪B={1,3}
A={1,3}, B={2,5}
A∪B=
2.4性质:
①A∩A=A;
⑤A∩B=A
A B;
④(A∩B) A;(A∩B) B;
②A∩ = ;
③A∩B=B∩A
新知2.交集
【例3】(1)设集合A={x|y=1/x},B={y|y=﹣x2+1},则A∩B=______.
(2)A={(x,y)|x-y=1},B={(x,y)|x+y=3},则A∩B=_______.
={x|x≠0}
={y|y≤1}
{t|t<0或0{(2,1)}
【例4】集合A={x|2a≤x≤a+3},B={x|x<﹣2或x>5},若A∩B= ,
则a的取值范围是__________.
[变式]A∩B≠
新知2.交集
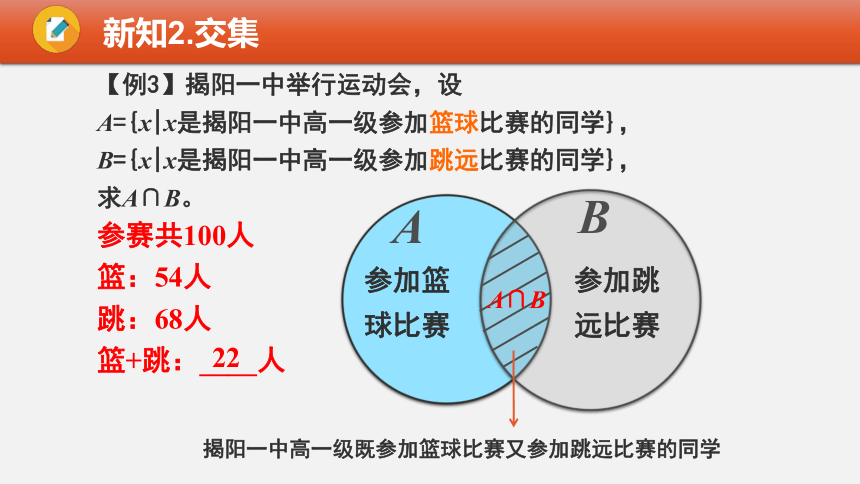
【例3】揭阳一中举行运动会,设
A={x|x是揭阳一中高一级参加篮球比赛的同学},
B={x|x是揭阳一中高一级参加跳远比赛的同学},
求A∩B。
A
B
参加篮球比赛
参加跳远比赛
揭阳一中高一级既参加篮球比赛又参加跳远比赛的同学
参赛共100人
篮:54人
跳:68人
篮+跳:____人
A∩B
22
把含有有限个元素的集合A叫做有限集;
用card来表示有限集合A中的元素个数.
如:A={1,2,3,5},则card(A)=4.
阅读与思考:集合中元素的个数
一般地,对于任意两个集合A、B,有:
card(A∪B)=card(A)+ card(B)-card(A∩B).
A
B
A∩B
①
②
③
①②③
①②
②③
②
card(A∪B∪C)=card(A)+card(B)+card(B)-card(A∩B)-card(A∩C)
-card(B∩C)+card(A∩B∩C)
新知2.交集 P12
【例4】设平面内直线l1上的点的集合为L1,直线l2上的点的集合为L2,试用集合的运算表示l1,l2的位置关系。
l1(l2)
L1∩L2={点P}
L1∩L2=
L1∩L2=L1=L2
L1∪L2=L1=L2
第一章 《集合与常用逻辑用语》
1.3 集合的基本运算(2)
问题引入
请分别求出方程(x-1)(x+2)(x2-5)=0的自然数解、有理数解、实数解构成的解集。
{x∈N|(x-1)(x+2)(x2-5)=0}={1}
{x∈Q|(x-1)(x+2)(x2-5)=0}={1,-2}
{x∈R|(x-1)(x+2)(x2-5)=0}=
可见,在不同的范围研究同一问题,结果可能不同。
全集:若一个集合含有所研究问题中涉及的所有元素,则称该集合为全集,通常记为U。
新知3.全集与补集
1.全集:若一个集合含有所研究问题中涉及的所有元素,则称该集合为全集,通常记为U。
U={1,2,3,4,5,6,7,8}
A={1,3,5,6,8}
U
A
1 3 5
6 8
2 4 7
{2,4,7}
{x|x∈U,且x∈A}
CUA=
UA
2.补集:由全集U中不属于A的所有元素组成的集合,称为集合A相对于全集U的补集,简称集合A的补集。
CUA={x|x∈U,且x∈A}
A
UA
新知3.全集与补集
A
UA
(1)符号语言:
(2)图形语言:
(3)性质:
CUA={x|x∈U,且x∈A}
①A∪(CUA)=___
A∩(CUA)=___
②CU(CUA)=___
U
A
CUU=___
CU =___
U
2.补集:由全集U中不属于A的所有元素组成的集合,称为集合A相对于全集U的补集,简称集合A的补集。
[练习]①若全集U={0,3,6,9},M={x|x2+ax=0},CUM={6,9},则a=____.
②若A={x|x>1},则CRA=__________.
③若B={x|1-3
{x|x≤1}
{x|x≤1或x>3}
新知基础巩固
M={0,3}
④若U={0,1,2,3,4},A={2,3},B={1,2,4},则B∩(CUA)=________.
CUA={0,1,4}
{1,4}
⑤若全集U={1,2,a2-2a+3},A={1,a},CRA={3},则实数a=______.
2
新知3.全集与补集P13
3.图中U是全集,A,B是U的两个子集,用阴影表示:
(1) (CUA)∩(CUB)
(2) (CUA)∪(CUB)
CUA:③④
CUB:①④
(CUA)∩(CUB):④
(CUA)∩(CUB)
A∪B
=CU(A∪B)
CUA:③④
CUB:①④
(CUA)∪(CUB):①③④
(CUA)∪(CUB)
=CU(A∩B)
德·摩根公式
A∩B
A={2,3,4,5}
B={0,4,5,6}
2,3
0,6
1,7
4,5
新知3.全集与补集
新知3.全集与补集
2.补集:
A
UA
(1)符号语言:
(2)图形语言:
(3)性质:
CUA={x|x∈U,且x∈A}
①A∪(CUA)=___
A∩(CUA)=___
②CU(CUA)=___
U
A
CUU=___
CU =___
U
③(CUA)∩(CUB)=CU(A∪B)
(CUA)∪(CUB)=CU(A∩B)
U={x∈N|x<6},
A={2,4,5},B={1,3,5}.
求(CUA)∪(CUB)
新知3.全集与补集
[练习]已知U=R,A={x|x2-x-2=0},B={x|mx+1=0},B∩(CRA)= ,求实数m的值.
∵B∩(CRA)= ,∴B A,则
A
CRA
B
A(B)
CRA
课后作业
1.设A={x|-2≤x≤0},B={x|2m-1A∪B=B,求实数m的取值范围.
【变式】设A={x|-2≤x≤5},B={x|2m-1≤x≤m},
若A∩B=B,求实数m的取值范围.
2.P12 B组第3题
升级巩固:集合的混合运算
升级巩固:根据集合运算结果求参数
A={0,1}
2
2
升级巩固:根据集合运算结果求参数
(1)已知A={x|-1≤x<4},B={x|x≥a},若A∩B≠ ,则实数a的取值构成的集合是____.
【变式】已知A={x|-1≤x<4},B={x|x≥a},若A∩B= ,则实数a的取值构成的集合是_____.
(2)设A={x|-2≤x≤5},B={x|2m-1{a|a<4}
{a|a≥4}
第一章 《集合与常用逻辑用语》
1.3 集合的基本运算(1)
实数间的大小关系
类比
集合间的包含关系
实数间的基本运算
类比
集合间的基本运算
加法运算
“相加”
观察下列各个集合,你能说出集合C与集合A,B之间的关系吗?
(1)A={1,3,5},B={2,4,6},C={1,2,3,4,5,6};
(2)A={x|x是有理数},B={x|x是无理数},C={x|x是实数};
(3)A={1,2,3},B={2,3,5,9},C={1,2,3,5,9}
C是由所有属于集合A或属于集合B的元素组成的.
类比实数的加法运算,你能否尝试定义集合间 “相加”运算?
课前思考
1∈A
5∈B
2∈A
且1∈B
且5∈A
且2∈B
称C是A和B的并集
只属于A
只属于B
属于A且属于B
1.1定义:由所有属于集合A或属于集合B的元素组成的集合,
叫做A和B的并集,记作A∪B,读作A并B。
新知1.并集
1.2符号语言:
A∪B={x|x∈A,或x∈B}
1.3图形语言:
A={1,3,5}, B={2,4,6}
A∪B={1,3,5,2,4,6}
A={1,3}, B={2,3,5}
A∪B={1,2,3,5}
A={1,3}, B={1,3,5}
A∪B={1,3,5}
1.4性质:
①A∪A=A;
⑤A∪B=B
A B;
[注]或的3个含义:①x∈A但x∈B;②x∈B但x∈A;③x∈A且x∈B
④A (A∪B);B (A∪B);
②A∪ =A;
③A∪B=B∪A
新知1.并集
【例2】设集合A={x|-2
A∪B={x|x<2}
公共元素在并集中只能出现一次(互异性)
看数轴
【例1】设A={2,3,6,8},B={3,5,7,8},则A∪B=________________.
【变式1】集合A={x|-2
{a|a≥2}
【变式2】集合A={x|x<1或x>3}, B={x|x
2.1定义:由所有属于集合A且属于集合B的元素组成的集合,
叫做A和B的交集,记作A∩B,读作A交B。
新知2.交集
2.2符号语言:
A∩B={x|x∈A,且x∈B}
2.3图形语言:
A={1,3,5}, B={2,3,5}
A∩B={3,5}
A={1,3}, B={1,3,5}
A∪B={1,3}
A={1,3}, B={2,5}
A∪B=
2.4性质:
①A∩A=A;
⑤A∩B=A
A B;
④(A∩B) A;(A∩B) B;
②A∩ = ;
③A∩B=B∩A
新知2.交集
【例3】(1)设集合A={x|y=1/x},B={y|y=﹣x2+1},则A∩B=______.
(2)A={(x,y)|x-y=1},B={(x,y)|x+y=3},则A∩B=_______.
={x|x≠0}
={y|y≤1}
{t|t<0或0
【例4】集合A={x|2a≤x≤a+3},B={x|x<﹣2或x>5},若A∩B= ,
则a的取值范围是__________.
[变式]A∩B≠
新知2.交集
【例3】揭阳一中举行运动会,设
A={x|x是揭阳一中高一级参加篮球比赛的同学},
B={x|x是揭阳一中高一级参加跳远比赛的同学},
求A∩B。
A
B
参加篮球比赛
参加跳远比赛
揭阳一中高一级既参加篮球比赛又参加跳远比赛的同学
参赛共100人
篮:54人
跳:68人
篮+跳:____人
A∩B
22
把含有有限个元素的集合A叫做有限集;
用card来表示有限集合A中的元素个数.
如:A={1,2,3,5},则card(A)=4.
阅读与思考:集合中元素的个数
一般地,对于任意两个集合A、B,有:
card(A∪B)=card(A)+ card(B)-card(A∩B).
A
B
A∩B
①
②
③
①②③
①②
②③
②
card(A∪B∪C)=card(A)+card(B)+card(B)-card(A∩B)-card(A∩C)
-card(B∩C)+card(A∩B∩C)
新知2.交集 P12
【例4】设平面内直线l1上的点的集合为L1,直线l2上的点的集合为L2,试用集合的运算表示l1,l2的位置关系。
l1(l2)
L1∩L2={点P}
L1∩L2=
L1∩L2=L1=L2
L1∪L2=L1=L2
第一章 《集合与常用逻辑用语》
1.3 集合的基本运算(2)
问题引入
请分别求出方程(x-1)(x+2)(x2-5)=0的自然数解、有理数解、实数解构成的解集。
{x∈N|(x-1)(x+2)(x2-5)=0}={1}
{x∈Q|(x-1)(x+2)(x2-5)=0}={1,-2}
{x∈R|(x-1)(x+2)(x2-5)=0}=
可见,在不同的范围研究同一问题,结果可能不同。
全集:若一个集合含有所研究问题中涉及的所有元素,则称该集合为全集,通常记为U。
新知3.全集与补集
1.全集:若一个集合含有所研究问题中涉及的所有元素,则称该集合为全集,通常记为U。
U={1,2,3,4,5,6,7,8}
A={1,3,5,6,8}
U
A
1 3 5
6 8
2 4 7
{2,4,7}
{x|x∈U,且x∈A}
CUA=
UA
2.补集:由全集U中不属于A的所有元素组成的集合,称为集合A相对于全集U的补集,简称集合A的补集。
CUA={x|x∈U,且x∈A}
A
UA
新知3.全集与补集
A
UA
(1)符号语言:
(2)图形语言:
(3)性质:
CUA={x|x∈U,且x∈A}
①A∪(CUA)=___
A∩(CUA)=___
②CU(CUA)=___
U
A
CUU=___
CU =___
U
2.补集:由全集U中不属于A的所有元素组成的集合,称为集合A相对于全集U的补集,简称集合A的补集。
[练习]①若全集U={0,3,6,9},M={x|x2+ax=0},CUM={6,9},则a=____.
②若A={x|x>1},则CRA=__________.
③若B={x|1
{x|x≤1}
{x|x≤1或x>3}
新知基础巩固
M={0,3}
④若U={0,1,2,3,4},A={2,3},B={1,2,4},则B∩(CUA)=________.
CUA={0,1,4}
{1,4}
⑤若全集U={1,2,a2-2a+3},A={1,a},CRA={3},则实数a=______.
2
新知3.全集与补集P13
3.图中U是全集,A,B是U的两个子集,用阴影表示:
(1) (CUA)∩(CUB)
(2) (CUA)∪(CUB)
CUA:③④
CUB:①④
(CUA)∩(CUB):④
(CUA)∩(CUB)
A∪B
=CU(A∪B)
CUA:③④
CUB:①④
(CUA)∪(CUB):①③④
(CUA)∪(CUB)
=CU(A∩B)
德·摩根公式
A∩B
A={2,3,4,5}
B={0,4,5,6}
2,3
0,6
1,7
4,5
新知3.全集与补集
新知3.全集与补集
2.补集:
A
UA
(1)符号语言:
(2)图形语言:
(3)性质:
CUA={x|x∈U,且x∈A}
①A∪(CUA)=___
A∩(CUA)=___
②CU(CUA)=___
U
A
CUU=___
CU =___
U
③(CUA)∩(CUB)=CU(A∪B)
(CUA)∪(CUB)=CU(A∩B)
U={x∈N|x<6},
A={2,4,5},B={1,3,5}.
求(CUA)∪(CUB)
新知3.全集与补集
[练习]已知U=R,A={x|x2-x-2=0},B={x|mx+1=0},B∩(CRA)= ,求实数m的值.
∵B∩(CRA)= ,∴B A,则
A
CRA
B
A(B)
CRA
课后作业
1.设A={x|-2≤x≤0},B={x|2m-1
【变式】设A={x|-2≤x≤5},B={x|2m-1≤x≤m},
若A∩B=B,求实数m的取值范围.
2.P12 B组第3题
升级巩固:集合的混合运算
升级巩固:根据集合运算结果求参数
A={0,1}
2
2
升级巩固:根据集合运算结果求参数
(1)已知A={x|-1≤x<4},B={x|x≥a},若A∩B≠ ,则实数a的取值构成的集合是____.
【变式】已知A={x|-1≤x<4},B={x|x≥a},若A∩B= ,则实数a的取值构成的集合是_____.
(2)设A={x|-2≤x≤5},B={x|2m-1
{a|a≥4}
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
