苏科版七年级上册2.2有理数与无理数课件(共21张PPT)
文档属性
| 名称 | 苏科版七年级上册2.2有理数与无理数课件(共21张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-19 09:06:30 | ||
图片预览







文档简介
(共21张PPT)
2.2 有理数与无理数
苏科版初中数学七年级上第2章有理数
下列哪些是整数 哪些是分数
正整数、负整数、零统称为整数.
整数
正分数
负分数
正分数、负分数统称为分数.
正整数
零
负整数
分数
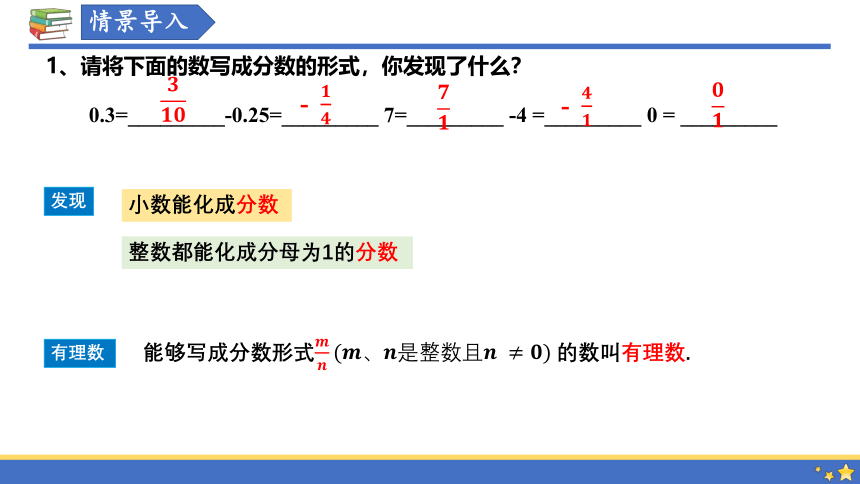
1、请将下面的数写成分数的形式,你发现了什么?
0.3=_________-0.25=_________ 7=_________ -4 =_________ 0 = _________
能够写成分数形式的数叫有理数.
-
-
整数都能化成分母为1的分数
小数能化成分数
发现
有理数
2、请将下面的分数写成小数的形式,你发现了什么?
分数可以写成有限小数或无限循环小数形式.
发现
例如,0.666…的循环节是“6”,它可以写作0. .像这样的循环小数称为纯循环小数;
循环小数
如果一个无限小数的各数位上的数字,从小数部分的某一位起,按一定顺序不断重复出现,那么这样的小数叫做无限循环小数,简称循环小数,其中重复出现的一个或几个数字叫做它的一个循环节.
又如,0.1333…、0.3456456456…的循环节分别为“3” 、“456”,它们可分别写作0.1 、0.3 5 .像这样的循环小数称为混循环小数.
纯循环小数
混循环小数
1.纯循环小数化为分数:
分数的分子是它的一个循环节的数字所组成的数,分母则由若干个9组成,9的个数为一个循环节的数字的个数。
例如: 0. =
2.混循环小数化为分数:先化为纯循环小数,然后再化为分数,
例如: 0.1 =×1.
0.3 5 3. 5
;
0. =
.
= ×(1+0. )
= + × =
= (3+0. 5 )
= + =
循环小数如何化为分数呢?
思考
3、小学里学过的有限小数和循环小数是有理数吗?
如:0.7,-5.31,0.333 …,0.2666.…
有限小数和循环小数都可以化为分数,它们都是有理数.
0.7=
-5.31=
0.333…==
0.2666…= = = +
归纳
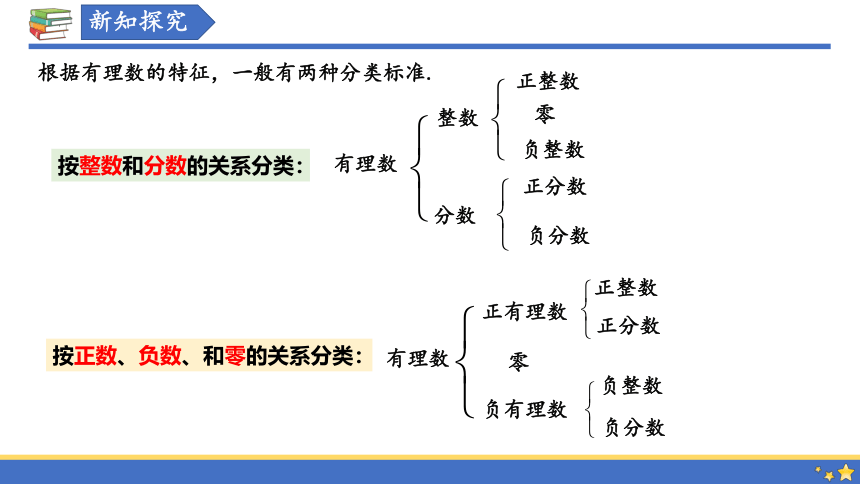
根据有理数的特征,一般有两种分类标准.
按整数和分数的关系分类:
按正数、负数、和零的关系分类:
有理数
正有理数
零
负有理数
正整数
正分数
负整数
负分数
正整数
零
负整数
整数
正分数
负分数
分数
有理数
正整数 整数 分数 正数 负数 有理数
0.83
+15
-0.89
-37
判断表中各数分别是什么数,在相应的空格内打“√”
√
√
√
√
√
√
√
√
√
√
√
√
√
√
√
√
正整数集合∶{ …}; 正分数集合∶{ …};
负整数集合∶{ …}; 负分数集合∶{ …};
整数集合∶{ …}; 分数集合∶ { …};
有理数集合∶ { …};
1.把后面各数填入相应的括号内∶ 20、-4.8、0、-13、+、 86%、-2020.
20、
-2 020、
+、
-4.8、
-2020、
-4.8、
-2020
20、
20、
-4.8、
0、
0、
-13、
-13、
-13、
86%、
+、
86%、
+、
86%、
将两个边长为1的小正方形,沿图中的红线剪开,重新拼成一个大正方形,它的面积为2。
1
1
1
1
如果设大正方形的边长为a ,那么a2 =2, a是有理数吗?
解析:a 能不能写成的形式,或者a是不是有限小数或无限循环小数。
可能是整数吗?
, , ……
整数的平方越来越大,2在1和4之间,所以应在1和2之间,
故不是整数。
可能是分数吗?
……
两个相同分数的乘积为分数,而 是整数,所以也不是分数。
边长 面积s=2
a是大于1小于2的数。
1.5
2.25
1.4
1.96
1.41.411.4141.41421.961.98811.9993961.99996164问题一:还可以继续确定a的取值范围吗
问题二:a可能是有限小数么
问题三:a可能是无限循环小数吗
可以
不可能
不可能
a不是有理数
借助计算器求得a=1.414213562373…,它是一个无限不循环小数。
如0.303 003 0003…、0.123 113 478 23…等
无限不循环小数叫做无理数
常见的形式
1.圆周率π及与π相关的一些数
2.看起来有规律的无限小数
无理数
1.判断:
(1)所有无限小数都是无理数. ( )
(2)所有无理数都是无限小数. ( )
(3)有理数都是有限小数. ( )
(4)不是有限小数的就不是有理数. ( )
×
√
×
×
2.在下列各数中,无理数的个数是( )
0.51515354…、0、、3π、、6.1010010001…、
A.1 B.2 C.3 D.4
C
3.下列说法∶①有理数就是有限小数; ②无限小数是无理数;
③无限不循环小数是无理数; ④
A.1个 B.2个 C.3个 D.4个
A
4.将下列各数分别填在相应的括号内:
﹣6,9.3,﹣,42,0 , -0.33 , 0.333…,1.41421356,﹣2π,
3.3030030003…,﹣3.1415926
正数集合{ …}
负数集合{ …}
有理数集合{ …}
无理数集合{ …}.
﹣3.1415926
﹣3.1415926
﹣6,
﹣6,
9.3,
9.3,
42,
42,
﹣ ,
﹣ ,
0,
-0.33 ,
-0.33 ,
0.333…,
0.333…,
1.41421356,
1.41421356,
﹣2π ,
﹣2π ,
3.3030030003…
3.3030030003…
5.把下列各数填在相应的集合内:
5,- ,0, 0.56, -3, , -0.0001, +2, -600, π
正整数集合:{ …};
负整数集合:{ …};
正分数集合:{ …};
负分数集合:{ …}.
5、
、
0.56、
-3、
-0.0001
+2
-600
6.把下列各数填在相应的大括号里:
- ,-7 ,-1. ,-3.2 ,0 ,1-π ,1 ,-22 ,
0.030030003 … (相邻两个3之间依次多一个0)。
非负整数集合:{ …};
分数集合:{ …};
无理数集合:{ … }.
1
-3.2
0.030030003 …
,
- 1. ,
0 ,
1-π ,
有理数
定义
分类
能够写成分数形式的数叫有理数.
无限不循环小数叫做无理数.
无理数
定义
负分数
有理数
正有理数
零
负有理数
正整数
正分数
负整数
正整数
零
负整数
整数
正分数
负分数
分数
有理数
谢 谢!
2.2 有理数与无理数
苏科版初中数学七年级上第2章有理数
下列哪些是整数 哪些是分数
正整数、负整数、零统称为整数.
整数
正分数
负分数
正分数、负分数统称为分数.
正整数
零
负整数
分数
1、请将下面的数写成分数的形式,你发现了什么?
0.3=_________-0.25=_________ 7=_________ -4 =_________ 0 = _________
能够写成分数形式的数叫有理数.
-
-
整数都能化成分母为1的分数
小数能化成分数
发现
有理数
2、请将下面的分数写成小数的形式,你发现了什么?
分数可以写成有限小数或无限循环小数形式.
发现
例如,0.666…的循环节是“6”,它可以写作0. .像这样的循环小数称为纯循环小数;
循环小数
如果一个无限小数的各数位上的数字,从小数部分的某一位起,按一定顺序不断重复出现,那么这样的小数叫做无限循环小数,简称循环小数,其中重复出现的一个或几个数字叫做它的一个循环节.
又如,0.1333…、0.3456456456…的循环节分别为“3” 、“456”,它们可分别写作0.1 、0.3 5 .像这样的循环小数称为混循环小数.
纯循环小数
混循环小数
1.纯循环小数化为分数:
分数的分子是它的一个循环节的数字所组成的数,分母则由若干个9组成,9的个数为一个循环节的数字的个数。
例如: 0. =
2.混循环小数化为分数:先化为纯循环小数,然后再化为分数,
例如: 0.1 =×1.
0.3 5 3. 5
;
0. =
.
= ×(1+0. )
= + × =
= (3+0. 5 )
= + =
循环小数如何化为分数呢?
思考
3、小学里学过的有限小数和循环小数是有理数吗?
如:0.7,-5.31,0.333 …,0.2666.…
有限小数和循环小数都可以化为分数,它们都是有理数.
0.7=
-5.31=
0.333…==
0.2666…= = = +
归纳
根据有理数的特征,一般有两种分类标准.
按整数和分数的关系分类:
按正数、负数、和零的关系分类:
有理数
正有理数
零
负有理数
正整数
正分数
负整数
负分数
正整数
零
负整数
整数
正分数
负分数
分数
有理数
正整数 整数 分数 正数 负数 有理数
0.83
+15
-0.89
-37
判断表中各数分别是什么数,在相应的空格内打“√”
√
√
√
√
√
√
√
√
√
√
√
√
√
√
√
√
正整数集合∶{ …}; 正分数集合∶{ …};
负整数集合∶{ …}; 负分数集合∶{ …};
整数集合∶{ …}; 分数集合∶ { …};
有理数集合∶ { …};
1.把后面各数填入相应的括号内∶ 20、-4.8、0、-13、+、 86%、-2020.
20、
-2 020、
+、
-4.8、
-2020、
-4.8、
-2020
20、
20、
-4.8、
0、
0、
-13、
-13、
-13、
86%、
+、
86%、
+、
86%、
将两个边长为1的小正方形,沿图中的红线剪开,重新拼成一个大正方形,它的面积为2。
1
1
1
1
如果设大正方形的边长为a ,那么a2 =2, a是有理数吗?
解析:a 能不能写成的形式,或者a是不是有限小数或无限循环小数。
可能是整数吗?
, , ……
整数的平方越来越大,2在1和4之间,所以应在1和2之间,
故不是整数。
可能是分数吗?
……
两个相同分数的乘积为分数,而 是整数,所以也不是分数。
边长 面积s=2
a是大于1小于2的数。
1.5
2.25
1.4
1.96
1.4
问题二:a可能是有限小数么
问题三:a可能是无限循环小数吗
可以
不可能
不可能
a不是有理数
借助计算器求得a=1.414213562373…,它是一个无限不循环小数。
如0.303 003 0003…、0.123 113 478 23…等
无限不循环小数叫做无理数
常见的形式
1.圆周率π及与π相关的一些数
2.看起来有规律的无限小数
无理数
1.判断:
(1)所有无限小数都是无理数. ( )
(2)所有无理数都是无限小数. ( )
(3)有理数都是有限小数. ( )
(4)不是有限小数的就不是有理数. ( )
×
√
×
×
2.在下列各数中,无理数的个数是( )
0.51515354…、0、、3π、、6.1010010001…、
A.1 B.2 C.3 D.4
C
3.下列说法∶①有理数就是有限小数; ②无限小数是无理数;
③无限不循环小数是无理数; ④
A.1个 B.2个 C.3个 D.4个
A
4.将下列各数分别填在相应的括号内:
﹣6,9.3,﹣,42,0 , -0.33 , 0.333…,1.41421356,﹣2π,
3.3030030003…,﹣3.1415926
正数集合{ …}
负数集合{ …}
有理数集合{ …}
无理数集合{ …}.
﹣3.1415926
﹣3.1415926
﹣6,
﹣6,
9.3,
9.3,
42,
42,
﹣ ,
﹣ ,
0,
-0.33 ,
-0.33 ,
0.333…,
0.333…,
1.41421356,
1.41421356,
﹣2π ,
﹣2π ,
3.3030030003…
3.3030030003…
5.把下列各数填在相应的集合内:
5,- ,0, 0.56, -3, , -0.0001, +2, -600, π
正整数集合:{ …};
负整数集合:{ …};
正分数集合:{ …};
负分数集合:{ …}.
5、
、
0.56、
-3、
-0.0001
+2
-600
6.把下列各数填在相应的大括号里:
- ,-7 ,-1. ,-3.2 ,0 ,1-π ,1 ,-22 ,
0.030030003 … (相邻两个3之间依次多一个0)。
非负整数集合:{ …};
分数集合:{ …};
无理数集合:{ … }.
1
-3.2
0.030030003 …
,
- 1. ,
0 ,
1-π ,
有理数
定义
分类
能够写成分数形式的数叫有理数.
无限不循环小数叫做无理数.
无理数
定义
负分数
有理数
正有理数
零
负有理数
正整数
正分数
负整数
正整数
零
负整数
整数
正分数
负分数
分数
有理数
谢 谢!
同课章节目录
- 第1章 我们与数学同行
- 1.1 生活 数学
- 1.2 活动 思考
- 第2章 有理数
- 2.1 正数与负数
- 2.2 有理数与无理数
- 2.3 数轴
- 2.4 绝对值与相反数
- 2.5 有理数的加法与减法
- 2.6 有理数的乘法与除法
- 2.7 有理数的乘方
- 2.8 有理数的混合运算
- 第3章 代数式
- 3.1 字母表示数
- 3.2 代数式
- 3.3 代数式的值
- 3.4 合并同类项
- 3.5 去括号
- 3.6 整式的加减
- 第4章 一元一次方程
- 4.1 从问题到方程
- 4.2 解一元一次方程
- 4.3 用一元一次方程解决问题
- 第5章 走进图形世界
- 5.1 丰富的图形世界
- 5.2 图形的运动
- 5.3 展开与折叠
- 5.4 主视图、左视图、俯视图
- 第6章 平面图形的认识(一)
- 6.1 线段 射线 直线
- 6.2 角
- 6.3 余角 补角 对顶角
- 6.4 平行
- 6.5 垂直
