2.3 二次函数与一元二次方程、不等式 课件(2课时)(共25张PPT)
文档属性
| 名称 | 2.3 二次函数与一元二次方程、不等式 课件(2课时)(共25张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1001.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-17 12:20:04 | ||
图片预览






文档简介
(共25张PPT)
2.3二次函数与一元
二次方程、不等式(1)
解一元二次不等式 如:求不等式x2+2x+3>0的解集
解分式不等式
解含绝对值的不等式
已知一元二次不等式的解集求参数
解含参数的一元二次不等式
一、基础概念
2.使一元二次不等式成立的的所有解x组成的集合叫做
一元二次不等式的解集(用集合的描述法表示).
ax2+bx+c>0;ax2+bx+c<0
ax2+bx+c≥0;ax2+bx+c≤0
其中a、b、c为常数,a≠0.
1.只含有一个未知数,且未知数的最高次数为2的不等式,
称为一元二次不等式。一般形式如下:
3.方程ax2+bx+c=0的实数解x叫做二次函数y=ax2+bx+c的零点.
2和10
-2
函数的零点
方程的根
函数图象与x轴交点横坐标
[注]①零点是数,不是点;②零点是函数的专属概念.
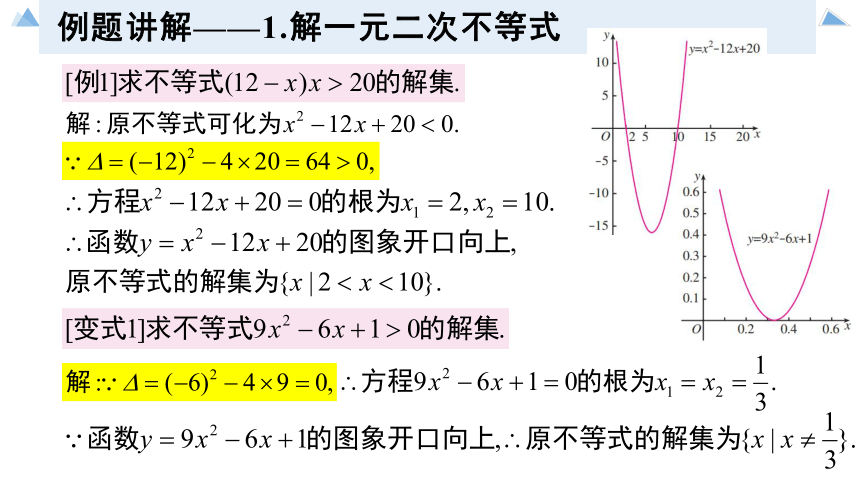
例题讲解——1.解一元二次不等式
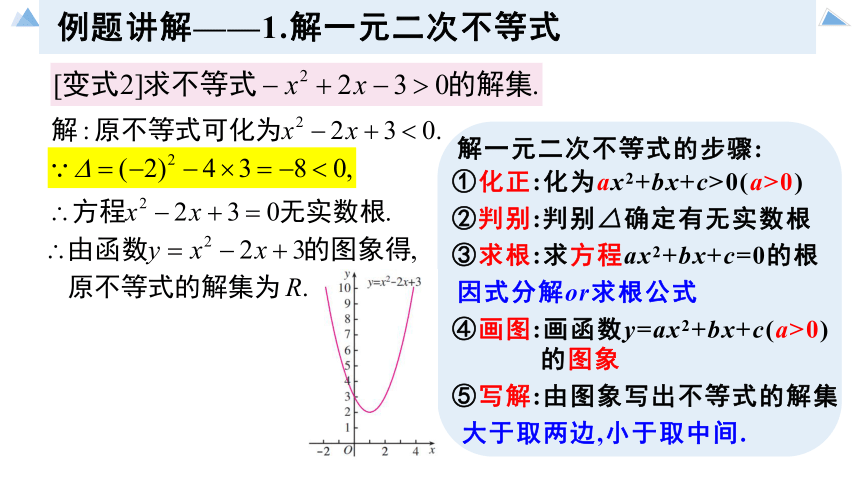
例题讲解——1.解一元二次不等式
解一元二次不等式的步骤:
①化正:化为ax2+bx+c>0(a>0)
③求根:求方程ax2+bx+c=0的根
④画图:画函数y=ax2+bx+c(a>0)
的图象
因式分解or求根公式
大于取两边,小于取中间.
②判别:判别△确定有无实数根
⑤写解:由图象写出不等式的解集
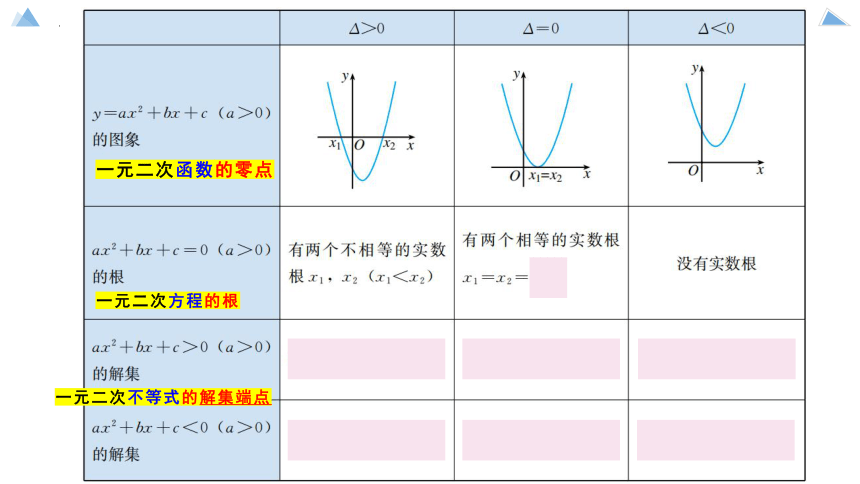
一元二次函数的零点
一元二次方程的根
一元二次不等式的解集端点
演练巩固——1.解一元二次不等式
x≤-4或x≥3
R
{x|1≤x≤3}
大于取两边
小于取中间
大于取两边
演练巩固——1.解一元二次不等式
∴原不等式的解集为{x|﹣2≤x≤﹣1或2≤x≤3}.
同时满足:
求交集
{x|-2≤x≤-1或2≤x≤3}
例题讲解——2.解分式不等式
同解变形(分母不为0!)
例题讲解——3.解绝对值不等式
-2x<-3或x>3
结论:①若|x|0),则-a②若|x|≥a(a>0),则x≤-a或x≥a.
推广:若|kx+b|0),则-a推广:若|kx+b|≥a(a>0),则kx+b≤-a或kx+b≥a.
小于取中间
大于取两边
例题讲解——3.解绝对值不等式
易错点:2x+1不确定正负,不能直接用|kx+b|0)的结论
{x|0{x|3≤x≤4或-4≤x≤-3}
分类讨论(<0、≥0)
2.3二次函数与一元
二次方程、不等式(2)
例题讲解——4.已知不等式的解集求参数
一元二次方程的根
一元二次不等式的解集端点
2
(法2)
(法1)
[变]求a-2b的值.
[变]求bx2+ax+1>0
的解集
例题讲解——4.已知不等式的解集求参数
(法1)
例题讲解——4.已知不等式的解集求参数
(法2)
例题讲解——5.恒成立问题
例题讲解——5.恒成立问题
>0
例题讲解——6.解含参数的一元二次不等式
化正(开口向上)→判别△→(△≥0)求根→画图→写解集
例题讲解——6.解含参数的一元二次不等式
②当a2a} .
若a=0,原式解集为{x|x≠0};
分类讨论的切入点:画图时需先比较根的大小
化正(开口向上)
→判别△
→(△≥0)求根
→画图
→写解集
①当a2>a,即a<0或a>1时,原式解集为{x|xa2}.
③当a2=a,即a=0或1时,
若a=1,原式解集为{x|x≠1}.
例题讲解——6.解含参数的一元二次不等式
化正
→判别△
→(△≥0)求根
→画图
→写解集
考虑a>0,a<0,a=0
比较根的大小
参数的分类讨论:
不重不漏
解含参数的一元二次不等式的思路
化正→判别△→(△≥0)求根→画图→写解集
课后作业
课后作业
课后作业
单击此处添加副标题内容
FIGHTING
2.3二次函数与一元
二次方程、不等式(1)
解一元二次不等式 如:求不等式x2+2x+3>0的解集
解分式不等式
解含绝对值的不等式
已知一元二次不等式的解集求参数
解含参数的一元二次不等式
一、基础概念
2.使一元二次不等式成立的的所有解x组成的集合叫做
一元二次不等式的解集(用集合的描述法表示).
ax2+bx+c>0;ax2+bx+c<0
ax2+bx+c≥0;ax2+bx+c≤0
其中a、b、c为常数,a≠0.
1.只含有一个未知数,且未知数的最高次数为2的不等式,
称为一元二次不等式。一般形式如下:
3.方程ax2+bx+c=0的实数解x叫做二次函数y=ax2+bx+c的零点.
2和10
-2
函数的零点
方程的根
函数图象与x轴交点横坐标
[注]①零点是数,不是点;②零点是函数的专属概念.
例题讲解——1.解一元二次不等式
例题讲解——1.解一元二次不等式
解一元二次不等式的步骤:
①化正:化为ax2+bx+c>0(a>0)
③求根:求方程ax2+bx+c=0的根
④画图:画函数y=ax2+bx+c(a>0)
的图象
因式分解or求根公式
大于取两边,小于取中间.
②判别:判别△确定有无实数根
⑤写解:由图象写出不等式的解集
一元二次函数的零点
一元二次方程的根
一元二次不等式的解集端点
演练巩固——1.解一元二次不等式
x≤-4或x≥3
R
{x|1≤x≤3}
大于取两边
小于取中间
大于取两边
演练巩固——1.解一元二次不等式
∴原不等式的解集为{x|﹣2≤x≤﹣1或2≤x≤3}.
同时满足:
求交集
{x|-2≤x≤-1或2≤x≤3}
例题讲解——2.解分式不等式
同解变形(分母不为0!)
例题讲解——3.解绝对值不等式
-2
结论:①若|x|
推广:若|kx+b|
小于取中间
大于取两边
例题讲解——3.解绝对值不等式
易错点:2x+1不确定正负,不能直接用|kx+b|
{x|0
分类讨论(<0、≥0)
2.3二次函数与一元
二次方程、不等式(2)
例题讲解——4.已知不等式的解集求参数
一元二次方程的根
一元二次不等式的解集端点
2
(法2)
(法1)
[变]求a-2b的值.
[变]求bx2+ax+1>0
的解集
例题讲解——4.已知不等式的解集求参数
(法1)
例题讲解——4.已知不等式的解集求参数
(法2)
例题讲解——5.恒成立问题
例题讲解——5.恒成立问题
>0
例题讲解——6.解含参数的一元二次不等式
化正(开口向上)→判别△→(△≥0)求根→画图→写解集
例题讲解——6.解含参数的一元二次不等式
②当a2
若a=0,原式解集为{x|x≠0};
分类讨论的切入点:画图时需先比较根的大小
化正(开口向上)
→判别△
→(△≥0)求根
→画图
→写解集
①当a2>a,即a<0或a>1时,原式解集为{x|x
③当a2=a,即a=0或1时,
若a=1,原式解集为{x|x≠1}.
例题讲解——6.解含参数的一元二次不等式
化正
→判别△
→(△≥0)求根
→画图
→写解集
考虑a>0,a<0,a=0
比较根的大小
参数的分类讨论:
不重不漏
解含参数的一元二次不等式的思路
化正→判别△→(△≥0)求根→画图→写解集
课后作业
课后作业
课后作业
单击此处添加副标题内容
FIGHTING
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
