2021-2022学年人教版八年级数学上册15.2.2分式的加减 (第1课时)课件(共20张PPT)
文档属性
| 名称 | 2021-2022学年人教版八年级数学上册15.2.2分式的加减 (第1课时)课件(共20张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-19 00:00:00 | ||
图片预览






文档简介
(共20张PPT)
15.2.3 分式的加减
15.2 分式的运算
1
1.理解分式的加减法法则,体会类比思想。
2.能对简单的分式进行加、减运算。
3.通过分式的加减运算体会化归思想。
2
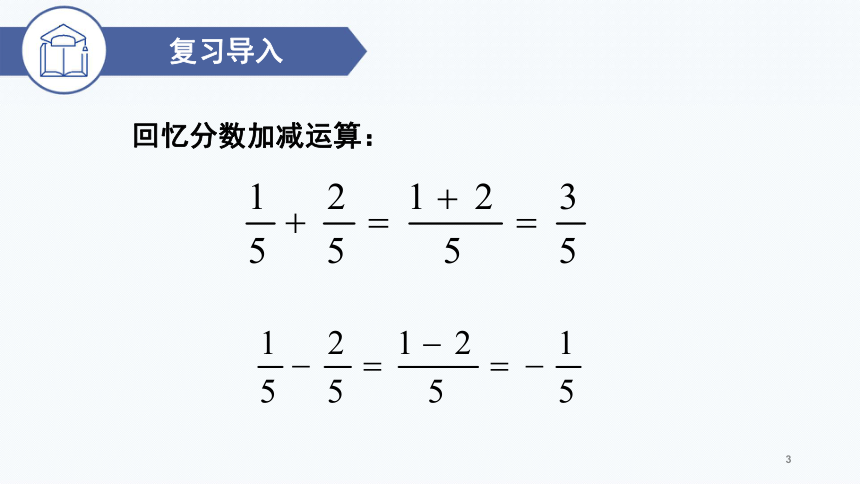
回忆分数加减运算:
3
复习导入
类比探究
观察分数加减运算的式子,猜想分式的加减运算:
请类比同分母分数的加减法,说一说同分母的分式应该如何加减?
同分母分式的加减
4
同分母分式的加减法则
同分母分式相加减,分母不变,把分子相加减。
上述法则可用式子表示为
同分母分式的加减
1
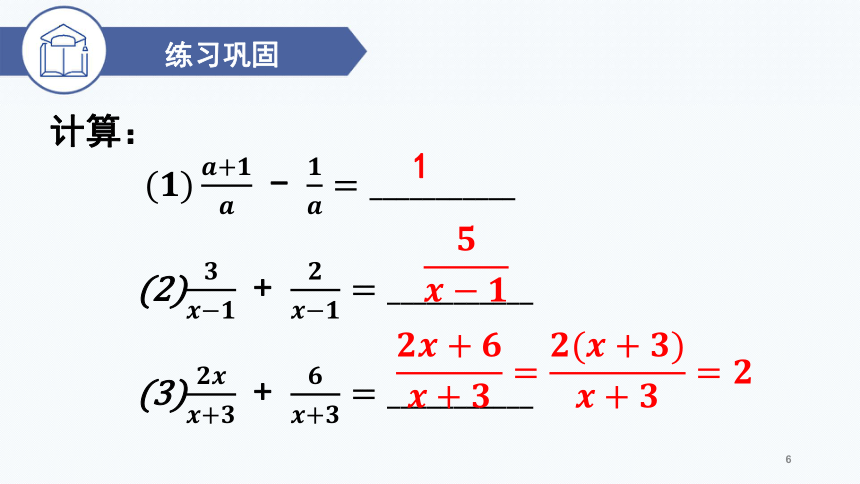
计算:
-
(2) +
(3) +
练习巩固
6
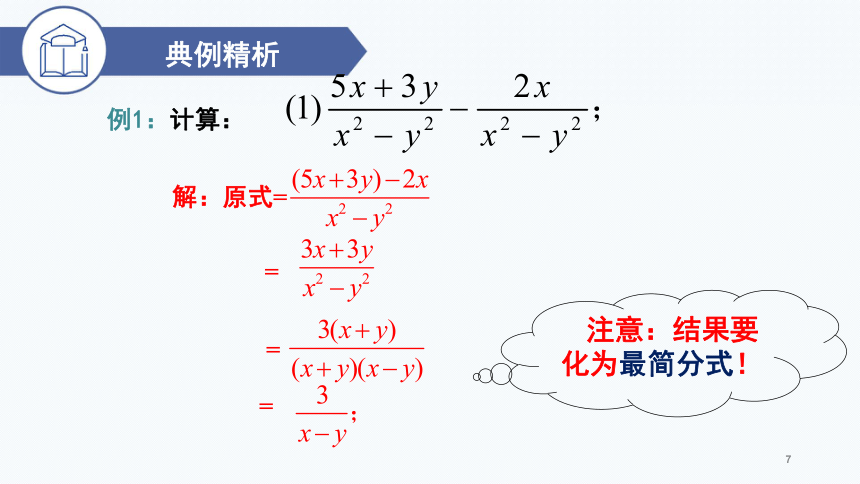
解:原式=
=
=
注意:结果要化为最简分式!
=
例1:计算:
典例精析
7
解:原式=
=
=
注意:结果要化为最简分式!
=
把分子看作一个整体,先用括号括起来!
(去括号)
(合并同类项)
8
典例精析
同分母分式相加减的一般步骤:
1.分母不变,把分子相加减。若分子是多项式,
则添加括号后相加减;
2.分子去括号,合并同类项;
3.把结果化成最简分式或整式。
方法总结
问题:
请计算 ( ), ( )
异分母分数相加减
分数的通分
依据:分数的基本性质
转化
同分母分数相加减
异分母分数相加减,先通分,
变为同分母的分数,再加减 。
异分母分式的加减
10
请计算 ( ), ( );
依据:分数基本性质
分数的通分
同分母分数相加减
异分母分数相加减
转化
异分母分数相加减,先通分,变为同分母的分数,再加减。
异分母分式相加减
分式的通分
依据:分式基本性质
转化
同分母分式相加减
异分母分式相加减,先通分,变为同分母的分式,再加减。
请思考
b
d
b
d
类比:异分母的分式应该如何加减
11
异分母分式的加减法则
异分母分式相加减,先通分,变同分母的分式,再加减.
上述法则可用式子表示为
异分母分式的加减
异分母分式相加减
同分母分式相加减
转化
解:原式=
=
=
注意:(1-x)=-(x-1)
例2:计算:
分母不同,先化为同分母。
13
典例精析
解:原式=
先找出最简公分母,再正确通分,转化为同分母的分式相加减。
14
典例精析
解:原式=
=
=
注意:分母是多项式先分解因式
先找出最简公分母,再正确通分,转化为同分母的分式相加减。
=
15
典例精析
分式的加减法的思路
通分
转化为
异分母相加减
同分母
相加减
分子(整式)
相加减
分母不变
转化为
异分母分式的加减
例3:计算:
法一:
原式=
法二:
原式=
把整式看成分母为“1”的分式
异分母分式的加减
17
18
典例精析
例4:计算:
解:原式
当m=1时,原式
从1、-3、3中任选一个你喜欢的m值代入求值
19
典例精析
例5:已知 =
解:
=
=
所以, 解得
分式加减运算
加减法运算
注意
(1)减式的分式是多项式时,在进行运算时要添加括号
异分母分式相加减先转化为同分母分式的加减运算
(2)整式和分式之间进行加减运算时,则要把整式看成分母是1的分式,以便通分
(3)异分母分式进行加减运算需要先通分,关键是确定最简公分母
课堂小结
20
15.2.3 分式的加减
15.2 分式的运算
1
1.理解分式的加减法法则,体会类比思想。
2.能对简单的分式进行加、减运算。
3.通过分式的加减运算体会化归思想。
2
回忆分数加减运算:
3
复习导入
类比探究
观察分数加减运算的式子,猜想分式的加减运算:
请类比同分母分数的加减法,说一说同分母的分式应该如何加减?
同分母分式的加减
4
同分母分式的加减法则
同分母分式相加减,分母不变,把分子相加减。
上述法则可用式子表示为
同分母分式的加减
1
计算:
-
(2) +
(3) +
练习巩固
6
解:原式=
=
=
注意:结果要化为最简分式!
=
例1:计算:
典例精析
7
解:原式=
=
=
注意:结果要化为最简分式!
=
把分子看作一个整体,先用括号括起来!
(去括号)
(合并同类项)
8
典例精析
同分母分式相加减的一般步骤:
1.分母不变,把分子相加减。若分子是多项式,
则添加括号后相加减;
2.分子去括号,合并同类项;
3.把结果化成最简分式或整式。
方法总结
问题:
请计算 ( ), ( )
异分母分数相加减
分数的通分
依据:分数的基本性质
转化
同分母分数相加减
异分母分数相加减,先通分,
变为同分母的分数,再加减 。
异分母分式的加减
10
请计算 ( ), ( );
依据:分数基本性质
分数的通分
同分母分数相加减
异分母分数相加减
转化
异分母分数相加减,先通分,变为同分母的分数,再加减。
异分母分式相加减
分式的通分
依据:分式基本性质
转化
同分母分式相加减
异分母分式相加减,先通分,变为同分母的分式,再加减。
请思考
b
d
b
d
类比:异分母的分式应该如何加减
11
异分母分式的加减法则
异分母分式相加减,先通分,变同分母的分式,再加减.
上述法则可用式子表示为
异分母分式的加减
异分母分式相加减
同分母分式相加减
转化
解:原式=
=
=
注意:(1-x)=-(x-1)
例2:计算:
分母不同,先化为同分母。
13
典例精析
解:原式=
先找出最简公分母,再正确通分,转化为同分母的分式相加减。
14
典例精析
解:原式=
=
=
注意:分母是多项式先分解因式
先找出最简公分母,再正确通分,转化为同分母的分式相加减。
=
15
典例精析
分式的加减法的思路
通分
转化为
异分母相加减
同分母
相加减
分子(整式)
相加减
分母不变
转化为
异分母分式的加减
例3:计算:
法一:
原式=
法二:
原式=
把整式看成分母为“1”的分式
异分母分式的加减
17
18
典例精析
例4:计算:
解:原式
当m=1时,原式
从1、-3、3中任选一个你喜欢的m值代入求值
19
典例精析
例5:已知 =
解:
=
=
所以, 解得
分式加减运算
加减法运算
注意
(1)减式的分式是多项式时,在进行运算时要添加括号
异分母分式相加减先转化为同分母分式的加减运算
(2)整式和分式之间进行加减运算时,则要把整式看成分母是1的分式,以便通分
(3)异分母分式进行加减运算需要先通分,关键是确定最简公分母
课堂小结
20
