20.1 多边形内角和(1)课件
图片预览


文档简介
课件13张PPT。尊敬的各位评委
您们好! 运用数学眼光,你能从下列现实生活的图案中找出一些平面图形吗? 在平面内,由 三条不在同一条直线上的线段首尾顺次相接组成的封闭图形叫三角形。 在平面内,由 四条不在同一条直线上的线
段首尾顺次相接组成的封闭图形叫四边形。 在平面内,由 五条不在同一条直线上的线
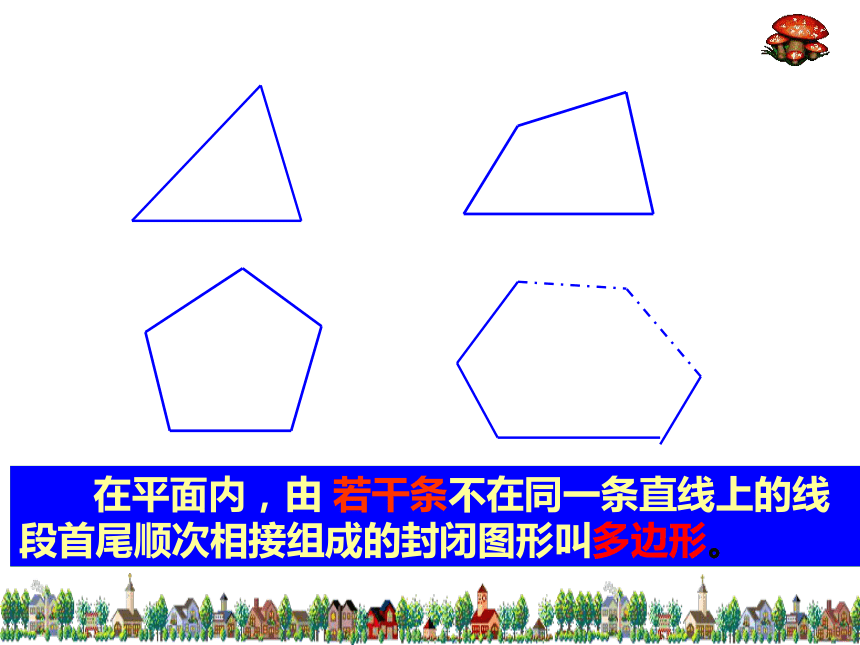
段首尾顺次相接组成的封闭图形叫五边形。 在平面内,由 若干条不在同一条直线上的线
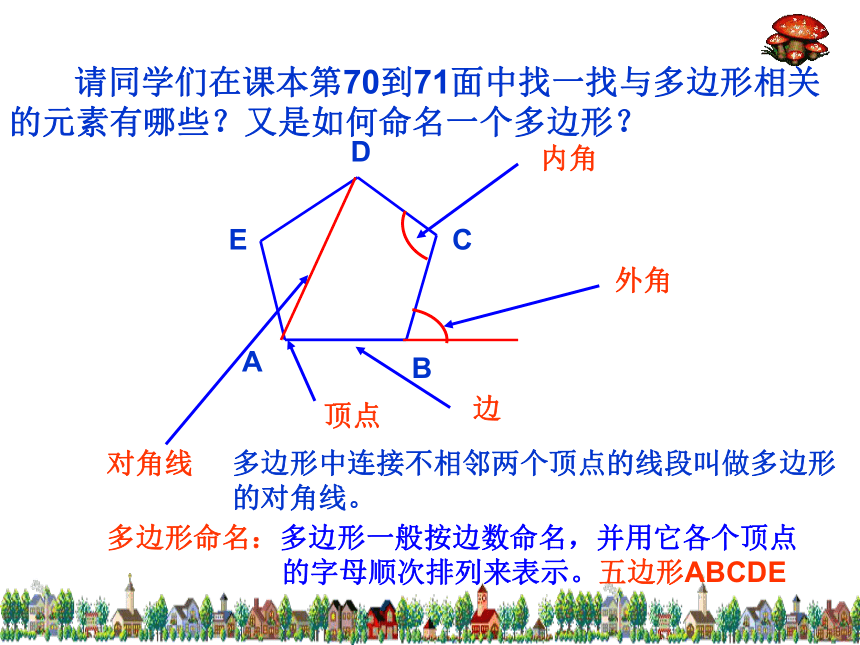
段首尾顺次相接组成的封闭图形叫多边形。 请同学们在课本第70到71面中找一找与多边形相关的元素有哪些?又是如何命名一个多边形?顶点边内角外角对角线多边形中连接不相邻两个顶点的线段叫做多边形的对角线。多边形命名:多边形一般按边数命名,并用它各个顶点
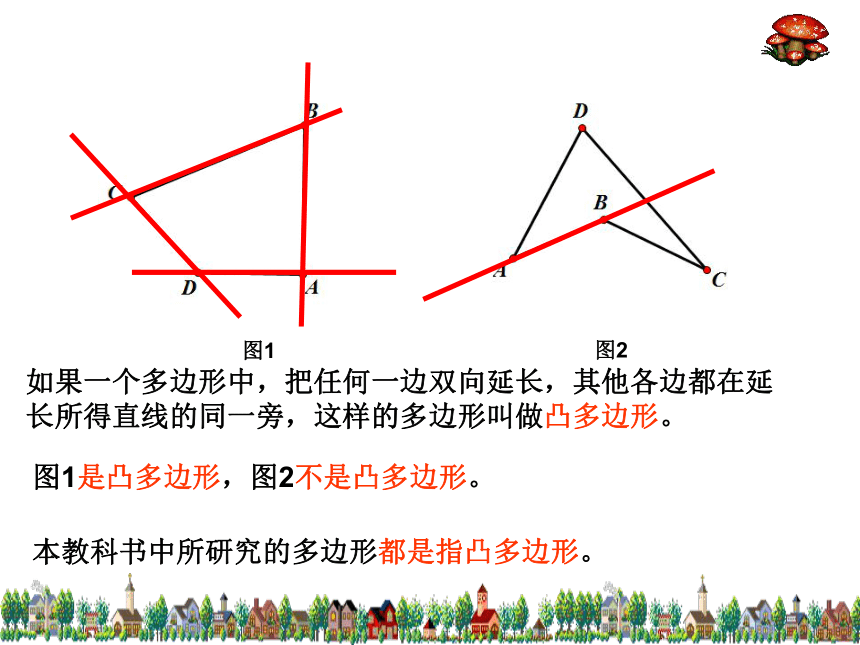
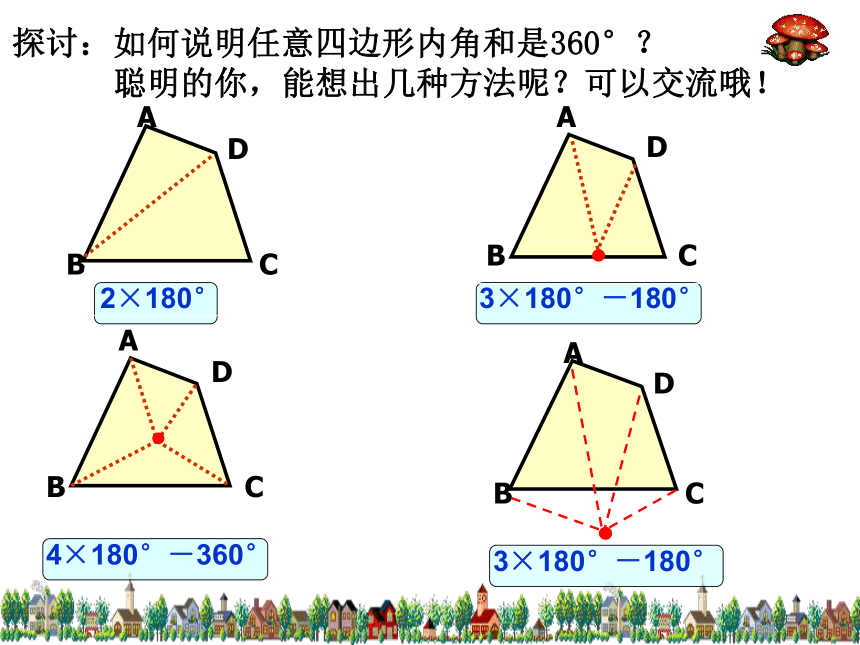
的字母顺次排列来表示。五边形ABCDE图1图2如果一个多边形中,把任何一边双向延长,其他各边都在延长所得直线的同一旁,这样的多边形叫做凸多边形。图1是凸多边形,图2不是凸多边形。本教科书中所研究的多边形都是指凸多边形。探讨:如何说明任意四边形内角和是360°?
聪明的你,能想出几种方法呢?可以交流哦!五边形的内角和又是多少呢?3×180°=540°452×180°3×180°32644×180°n…………n-2(n-2)·180°从一个顶点出发,引出它的所有对角线,则有:证明: 从n边形的一个顶点出发引出它的所有对角线
有 条;(n — 3)这时n边形被分成了 个三角形,由于每一个三角形的内角和为180○,因此n边形的内角和就等于求证:n边形的内角和
等于(n—2)·180°(n — 2)(n — 2)● 180○甲:说出一个多边形的边数;
乙:说出过一个多边形一个顶点的所有对角线分割出的
三角形个数;
丙:说出一个多边形的内角和。当甲先说时,乙、丙作答;
当乙先说时,甲、丙作答;
当丙先说时,甲、乙作答。互动游戏 巩固新知规则 若一个四边形的四个内角度数之比是1:2:3:4,求这四个内角的度数。 通过本节课的学习活动,你有了哪些收获?那个地方令你印象最深?
自主总结 全面提高1、我们认识了多边形及其相关元素,知道怎样命名一个多
边形;2、通过探索多边形内角和公式,我们尝试了用不同的方法
得出结果,并能运用多边形内角和公式进行计算或建立
方程解决问题;3、我们在探索多边形内角和时,首先从我们已知的三角形
内角和出发,先探索了四边形和五边形的内角和,再运
用得到的方法去解决n边形的内角和。这种把新知识转化
为已学知识,探索时又运用特殊到一般的研究数学问题的
思想方法是我们在学习数学过程中经常要用的,希望同学
们能认真领悟这种思想方法。清点收获分层作业谢谢大家
敬请指导!
您们好! 运用数学眼光,你能从下列现实生活的图案中找出一些平面图形吗? 在平面内,由 三条不在同一条直线上的线段首尾顺次相接组成的封闭图形叫三角形。 在平面内,由 四条不在同一条直线上的线
段首尾顺次相接组成的封闭图形叫四边形。 在平面内,由 五条不在同一条直线上的线
段首尾顺次相接组成的封闭图形叫五边形。 在平面内,由 若干条不在同一条直线上的线
段首尾顺次相接组成的封闭图形叫多边形。 请同学们在课本第70到71面中找一找与多边形相关的元素有哪些?又是如何命名一个多边形?顶点边内角外角对角线多边形中连接不相邻两个顶点的线段叫做多边形的对角线。多边形命名:多边形一般按边数命名,并用它各个顶点
的字母顺次排列来表示。五边形ABCDE图1图2如果一个多边形中,把任何一边双向延长,其他各边都在延长所得直线的同一旁,这样的多边形叫做凸多边形。图1是凸多边形,图2不是凸多边形。本教科书中所研究的多边形都是指凸多边形。探讨:如何说明任意四边形内角和是360°?
聪明的你,能想出几种方法呢?可以交流哦!五边形的内角和又是多少呢?3×180°=540°452×180°3×180°32644×180°n…………n-2(n-2)·180°从一个顶点出发,引出它的所有对角线,则有:证明: 从n边形的一个顶点出发引出它的所有对角线
有 条;(n — 3)这时n边形被分成了 个三角形,由于每一个三角形的内角和为180○,因此n边形的内角和就等于求证:n边形的内角和
等于(n—2)·180°(n — 2)(n — 2)● 180○甲:说出一个多边形的边数;
乙:说出过一个多边形一个顶点的所有对角线分割出的
三角形个数;
丙:说出一个多边形的内角和。当甲先说时,乙、丙作答;
当乙先说时,甲、丙作答;
当丙先说时,甲、乙作答。互动游戏 巩固新知规则 若一个四边形的四个内角度数之比是1:2:3:4,求这四个内角的度数。 通过本节课的学习活动,你有了哪些收获?那个地方令你印象最深?
自主总结 全面提高1、我们认识了多边形及其相关元素,知道怎样命名一个多
边形;2、通过探索多边形内角和公式,我们尝试了用不同的方法
得出结果,并能运用多边形内角和公式进行计算或建立
方程解决问题;3、我们在探索多边形内角和时,首先从我们已知的三角形
内角和出发,先探索了四边形和五边形的内角和,再运
用得到的方法去解决n边形的内角和。这种把新知识转化
为已学知识,探索时又运用特殊到一般的研究数学问题的
思想方法是我们在学习数学过程中经常要用的,希望同学
们能认真领悟这种思想方法。清点收获分层作业谢谢大家
敬请指导!
