新课标苏教版六上1.7《长方体和正方体的体积》课件(41张PPT)
文档属性
| 名称 | 新课标苏教版六上1.7《长方体和正方体的体积》课件(41张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-17 17:50:52 | ||
图片预览







文档简介
(共41张PPT)
长方体和正方体的体积
苏教版六年级上册
教学目标
1.学习目标描述:经历操作、观察、猜想、验证等数学活动的过程,探索并掌握长方体和正方体的体积公式,能运用公式正确计算长方体和正方体的体积。
2.学习内容分析:本节所学的内容是在学生已经认识了长方体和正方体的特征、学习了表面积的计算,掌握了体积的概念和常用的体积单位的基础上, 引导学生探索并掌握长方体和正方体的体积公式,并应用公式解决一些简单的实际问题。初步掌握长方体和正方体体积公式的基
教学目标
础上, 引导学生进一步探索长方体和正方体的体积公式,在探索中通过分析、比较、归纳,掌握”长方体(正方体)的体积=底面积×高”这一体积的统一公式。
3.学科核心素养分析:使学生在活动中进一步积累空间与图形的学习经验,增强空间观念,发展数学思考;进一步体会图形学习与实际生活的联系,感受图形学习的价值,提高数学学习的兴趣和学好数学的自信心。
新知导入
1.填一填。
棱长是1cm的正方体,体积是( )。
棱长是1dm的正方体,体积是( )。
棱长是1m的正方体,体积是( )。
1立方分米=( )升 1立方厘米=( )毫升
1cm3
1dm3
1m3
1
1
新知导入
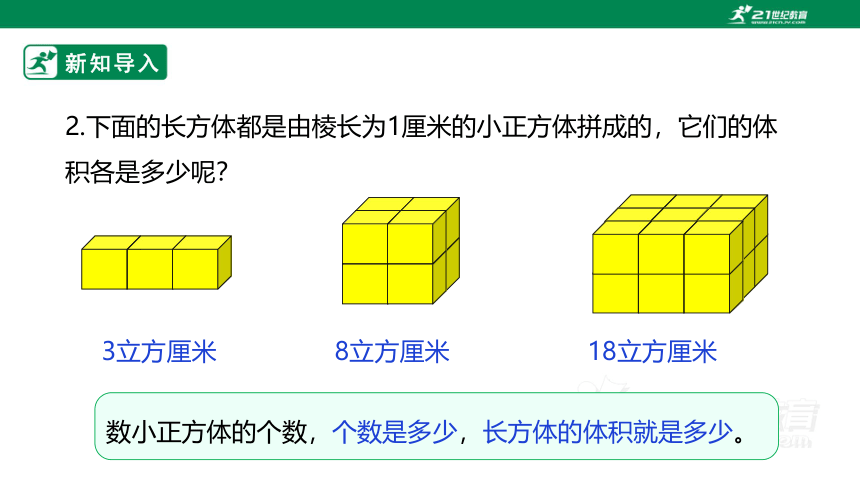
2.下面的长方体都是由棱长为1厘米的小正方体拼成的,它们的体积各是多少呢?
3立方厘米
8立方厘米
数小正方体的个数,个数是多少,长方体的体积就是多少。
18立方厘米
新知导入
把它切分成棱长1cm的小正方体。
这是我们常用的橡皮,怎样才能知道它的体积呢?结合上节课学习的内容说一说。
是不是所有的长方体体积都可以这样求?
像冰箱、洗衣机等这样的大型家电,就不能切割,也不好用正方体来摆。
新知讲解
下图是由体积为1立方厘米的小正方体组成的,摆成的长方体的长、宽、高各是多少?用了多少小正方体?包含多少个体积单位?
摆成长方体的长是3厘米,宽和高都是2厘米。
3×2×2=12(个),用了12个小正方体。
包含12个体积单位,长方体的体积是12立方厘米。
新知讲解
小组合作,用若干个1立方厘米的小正方体摆出不同的长方体,并填写右表。
新知讲解
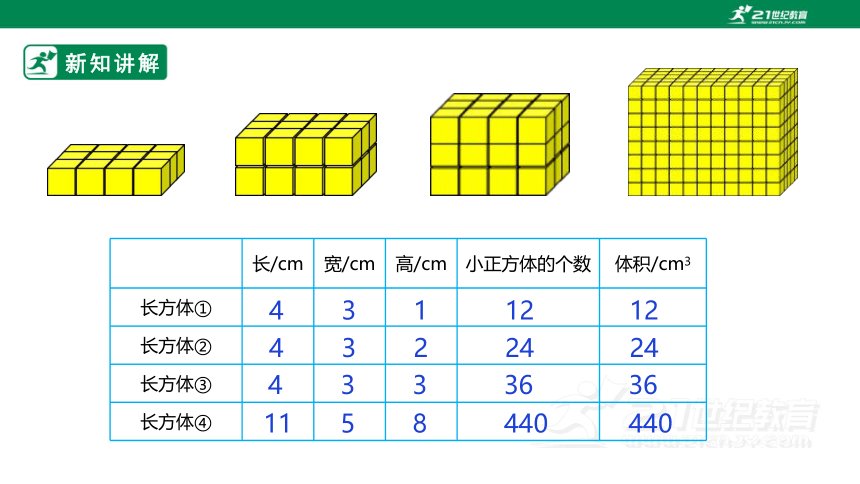
长/cm 宽/cm 高/cm 小正方体的个数 体积/cm3
长方体①
长方体②
长方体③
长方体④
4
3
1
12
12
4
3
2
24
24
4
3
3
36
36
11
5
8
440
440
新知讲解
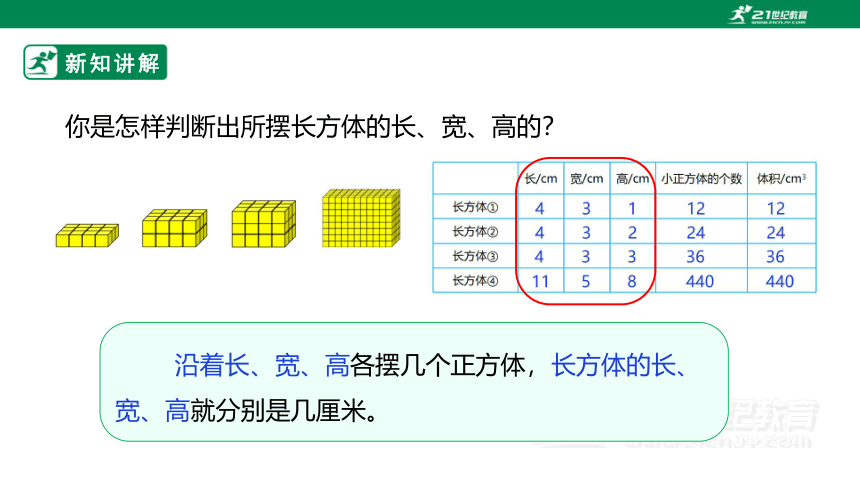
你是怎样判断出所摆长方体的长、宽、高的?
沿着长、宽、高各摆几个正方体,长方体的长、宽、高就分别是几厘米。
新知讲解
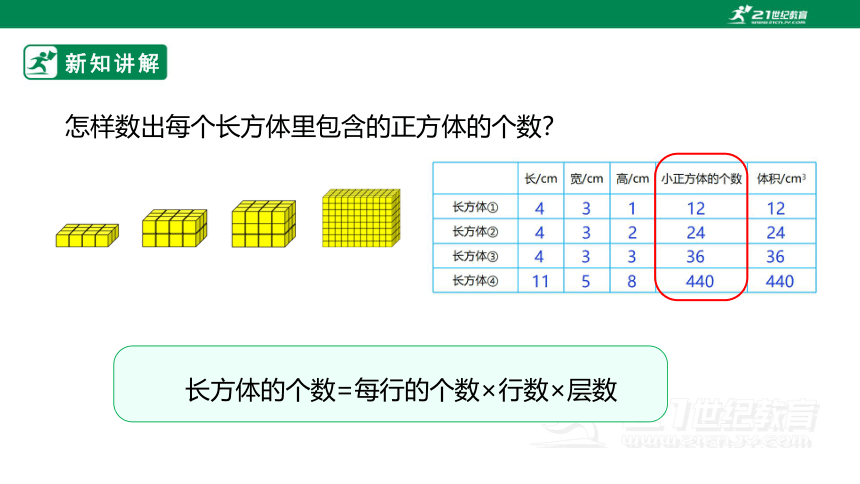
怎样数出每个长方体里包含的正方体的个数?
长方体的个数=每行的个数×行数×层数
新知讲解
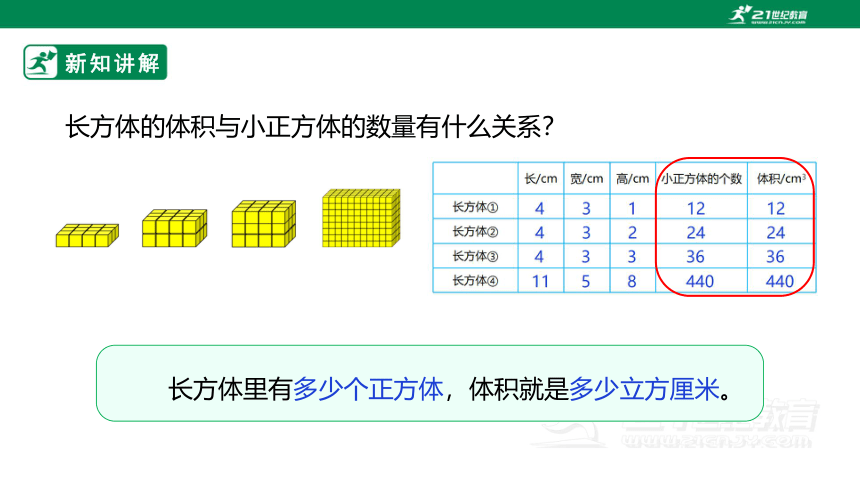
长方体的体积与小正方体的数量有什么关系?
长方体里有多少个正方体,体积就是多少立方厘米。
新知讲解
用1立方厘米的小正方体摆出下面的长方体,各需要多少个?先想一想,再摆一摆。
4㎝
1㎝
1㎝
4㎝
1㎝
3㎝
4㎝
2㎝
3㎝
这3个长方体的体积各是多少立方厘米?
新知讲解
4㎝
1㎝
1㎝
1㎝
1㎝
1㎝
1㎝
1㎝
1㎝
长方体的宽与高都是1厘米,只要把4个正方体摆成一行。
长方体长的数量是4,沿着长摆出4个体积单位。
4×1=4(个),长与宽的乘积,就是一行里体积单位的个数,体积是4cm3。
新知讲解
4㎝
1㎝
1㎝
1㎝
1㎝
1㎝
1㎝
1㎝
1㎝
长方体长的数量与沿着长摆的体积单位个数是一致的。
新知讲解
长方体的高1厘米,只要把正方体摆成一层。
4㎝
1㎝
3㎝
1㎝
1㎝
1㎝
1㎝
1㎝
长方体宽的数量是3,沿着宽应该摆出3行体积单位。
4×3=12(个),长与宽的乘积,就是一层里体积单位的个数,体积是12cm3。
新知讲解
长方体高2厘米,要把正方体摆成2层。
4㎝
2㎝
3㎝
1㎝
1㎝
1㎝
1㎝
1㎝
1㎝
长方体高的数量是2,沿着高摆出2层体积单位。
4×3×2=24(个),长乘宽乘高的乘积,就是2层体积单位的个数,体积是24cm3。
新知讲解
从上面的两次摆一摆中,你发现长方体的体积与什么有关?
4厘米
3厘米
2厘米
长:4厘米
宽:3厘米
高:2厘米
体积:24立方厘米
长方体的体积应该与长、宽、高有关。
长方体的体积=长×宽×高
新知讲解
如果用V表示长方体的体积,用a、b、h分别表示长、宽、高,上面的公式可以写成:
a
b
h
长方体的体积=长×宽×高
…
…
…
…
=
·
·
=
新知讲解
正方体的棱长有什么特点?可以怎样求正方体的体积?与同学交流你的想法。
正方体12条棱长度相等
每行摆的个数、摆的行数、摆的层数都与正方体的棱长相等。
正方体的体积=棱长×棱长×棱长
新知讲解
如果用V表体积,用a表示棱长,上面的公式可以写成:
a
a
a
正方体的体积=棱长×棱长×棱长
=
·
·
=
读作a的立方
a 表示3个a相乘
新知讲解
试一试
计算下面长方体和正方体包装盒的体积。
30×8×10=
2400(立方厘米)
12×12×12=
1728(立方厘米)
新知讲解
底面就是长方体和正方体的下面。
一个长方体的6个面中,任何一个面都可以做底面,一般以水平放置的下面做底面。
找出这两个图形的底面。
新知讲解
这两个图形的底面积是哪个面的面积?
长方体和正方体底面的面积,叫作它们的底面积。
新知讲解
长方体和正方体的底面面积怎么计算?
长
宽
长方体的底面积=长×宽
棱长
棱长
正方体的底面积=棱长×棱长
新知讲解
想一想,长方体和正方体的体积还可以怎么计算?并说说这个公式是怎样得到的?
长方体的体积=长×宽×高
底面积
= ×高
底面积
高
新知讲解
想一想,长方体和正方体的体积还可以怎么计算?并说说这个公式是怎样得到的?
正方体的体积=棱长×棱长×棱长
底面积
= ×棱长
底面积
棱长
相当于正方体的高。
=底面积×高
新知讲解
底面积
高
底面积
高
长方体和正方体的体积公式可以统一为:
长方体(或正方体)的体积=底面积×高
如果用S表示底面积,体积公式可以写成:
V=Sh
新知讲解
在解决求体积的些实际问题时, 可以直接用它的底面积(或先求出底面积)乘高就可以了。
新知讲解
长方体和正方体不同放置,说法各不相同。
横截面
长
横截面
长
长方体和正方体的侧面叫做横截面。
新知讲解
以长方体为例,说说横截面、长与底面积、高有什么关系呢?
横截面
长
底面积
高
横截面相当于底面积,长相当于高。
长方体(或正方体)的体积=横截面积×长
课堂练习
1.计算。
13= 23= 33= 43= 53=
63= 73= 83= 93= 103=
1
8
27
64
125
216
343
512
729
1000
课堂练习
2.填一填。
长方体 底面积(cm2) 12 30 9
高(cm) 7 12 8
体积(cm3) 96 22.5
84
360
12
2.5
课堂练习
3.一块正方体石料,棱长4分米,如果每立方分米2.7千克,这块石料重多少千克?
4×4×4×2.7
=64×2.7
=172.8(千克)
答:这块石料重172.8千克。
课堂练习
4.一个长方体的横截面是边长为3cm的正方形,它的长是5dm,这个长方体的体积是多少?
5分米=50厘米
3×3×50=450(立方厘米)
答:这个长方形的体积450立方厘米。
课堂练习
4.拓展应用:将一根横截面是10厘米的正方形的长方体木料,沿着横截面截成两段,表面积增加了200平方厘米,若这根木料长为2米,则这根木料的体积是多少立方米?
沿着横截面截成两段,表面积增加了两个面,2个横截面的面积。
10×10×2=200(平方厘米)
200平方厘米=0.02平方米
0.02×2=0.04(立方米)
答:则这根木料的体积是0.04立方米。
课堂总结
通过今天的学习,你有哪些收获?
我会计算长方体和正方体的体积了。
我还知道了长方体和正方体的统一公式。
板书设计
长方体的体积
长方体的体积=长×宽×高
V=a·b·h = abh
正方体的体积=棱长×棱长×棱长
V=a·a·a=a3 (读作:a的立方)
长方体(或正方体)的体积=底面积×高
V=Sh
长方体(或正方体)的体积=横截面积×长
作业布置
完成课本第17、18页“练一练”习题。
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
长方体和正方体的体积
苏教版六年级上册
教学目标
1.学习目标描述:经历操作、观察、猜想、验证等数学活动的过程,探索并掌握长方体和正方体的体积公式,能运用公式正确计算长方体和正方体的体积。
2.学习内容分析:本节所学的内容是在学生已经认识了长方体和正方体的特征、学习了表面积的计算,掌握了体积的概念和常用的体积单位的基础上, 引导学生探索并掌握长方体和正方体的体积公式,并应用公式解决一些简单的实际问题。初步掌握长方体和正方体体积公式的基
教学目标
础上, 引导学生进一步探索长方体和正方体的体积公式,在探索中通过分析、比较、归纳,掌握”长方体(正方体)的体积=底面积×高”这一体积的统一公式。
3.学科核心素养分析:使学生在活动中进一步积累空间与图形的学习经验,增强空间观念,发展数学思考;进一步体会图形学习与实际生活的联系,感受图形学习的价值,提高数学学习的兴趣和学好数学的自信心。
新知导入
1.填一填。
棱长是1cm的正方体,体积是( )。
棱长是1dm的正方体,体积是( )。
棱长是1m的正方体,体积是( )。
1立方分米=( )升 1立方厘米=( )毫升
1cm3
1dm3
1m3
1
1
新知导入
2.下面的长方体都是由棱长为1厘米的小正方体拼成的,它们的体积各是多少呢?
3立方厘米
8立方厘米
数小正方体的个数,个数是多少,长方体的体积就是多少。
18立方厘米
新知导入
把它切分成棱长1cm的小正方体。
这是我们常用的橡皮,怎样才能知道它的体积呢?结合上节课学习的内容说一说。
是不是所有的长方体体积都可以这样求?
像冰箱、洗衣机等这样的大型家电,就不能切割,也不好用正方体来摆。
新知讲解
下图是由体积为1立方厘米的小正方体组成的,摆成的长方体的长、宽、高各是多少?用了多少小正方体?包含多少个体积单位?
摆成长方体的长是3厘米,宽和高都是2厘米。
3×2×2=12(个),用了12个小正方体。
包含12个体积单位,长方体的体积是12立方厘米。
新知讲解
小组合作,用若干个1立方厘米的小正方体摆出不同的长方体,并填写右表。
新知讲解
长/cm 宽/cm 高/cm 小正方体的个数 体积/cm3
长方体①
长方体②
长方体③
长方体④
4
3
1
12
12
4
3
2
24
24
4
3
3
36
36
11
5
8
440
440
新知讲解
你是怎样判断出所摆长方体的长、宽、高的?
沿着长、宽、高各摆几个正方体,长方体的长、宽、高就分别是几厘米。
新知讲解
怎样数出每个长方体里包含的正方体的个数?
长方体的个数=每行的个数×行数×层数
新知讲解
长方体的体积与小正方体的数量有什么关系?
长方体里有多少个正方体,体积就是多少立方厘米。
新知讲解
用1立方厘米的小正方体摆出下面的长方体,各需要多少个?先想一想,再摆一摆。
4㎝
1㎝
1㎝
4㎝
1㎝
3㎝
4㎝
2㎝
3㎝
这3个长方体的体积各是多少立方厘米?
新知讲解
4㎝
1㎝
1㎝
1㎝
1㎝
1㎝
1㎝
1㎝
1㎝
长方体的宽与高都是1厘米,只要把4个正方体摆成一行。
长方体长的数量是4,沿着长摆出4个体积单位。
4×1=4(个),长与宽的乘积,就是一行里体积单位的个数,体积是4cm3。
新知讲解
4㎝
1㎝
1㎝
1㎝
1㎝
1㎝
1㎝
1㎝
1㎝
长方体长的数量与沿着长摆的体积单位个数是一致的。
新知讲解
长方体的高1厘米,只要把正方体摆成一层。
4㎝
1㎝
3㎝
1㎝
1㎝
1㎝
1㎝
1㎝
长方体宽的数量是3,沿着宽应该摆出3行体积单位。
4×3=12(个),长与宽的乘积,就是一层里体积单位的个数,体积是12cm3。
新知讲解
长方体高2厘米,要把正方体摆成2层。
4㎝
2㎝
3㎝
1㎝
1㎝
1㎝
1㎝
1㎝
1㎝
长方体高的数量是2,沿着高摆出2层体积单位。
4×3×2=24(个),长乘宽乘高的乘积,就是2层体积单位的个数,体积是24cm3。
新知讲解
从上面的两次摆一摆中,你发现长方体的体积与什么有关?
4厘米
3厘米
2厘米
长:4厘米
宽:3厘米
高:2厘米
体积:24立方厘米
长方体的体积应该与长、宽、高有关。
长方体的体积=长×宽×高
新知讲解
如果用V表示长方体的体积,用a、b、h分别表示长、宽、高,上面的公式可以写成:
a
b
h
长方体的体积=长×宽×高
…
…
…
…
=
·
·
=
新知讲解
正方体的棱长有什么特点?可以怎样求正方体的体积?与同学交流你的想法。
正方体12条棱长度相等
每行摆的个数、摆的行数、摆的层数都与正方体的棱长相等。
正方体的体积=棱长×棱长×棱长
新知讲解
如果用V表体积,用a表示棱长,上面的公式可以写成:
a
a
a
正方体的体积=棱长×棱长×棱长
=
·
·
=
读作a的立方
a 表示3个a相乘
新知讲解
试一试
计算下面长方体和正方体包装盒的体积。
30×8×10=
2400(立方厘米)
12×12×12=
1728(立方厘米)
新知讲解
底面就是长方体和正方体的下面。
一个长方体的6个面中,任何一个面都可以做底面,一般以水平放置的下面做底面。
找出这两个图形的底面。
新知讲解
这两个图形的底面积是哪个面的面积?
长方体和正方体底面的面积,叫作它们的底面积。
新知讲解
长方体和正方体的底面面积怎么计算?
长
宽
长方体的底面积=长×宽
棱长
棱长
正方体的底面积=棱长×棱长
新知讲解
想一想,长方体和正方体的体积还可以怎么计算?并说说这个公式是怎样得到的?
长方体的体积=长×宽×高
底面积
= ×高
底面积
高
新知讲解
想一想,长方体和正方体的体积还可以怎么计算?并说说这个公式是怎样得到的?
正方体的体积=棱长×棱长×棱长
底面积
= ×棱长
底面积
棱长
相当于正方体的高。
=底面积×高
新知讲解
底面积
高
底面积
高
长方体和正方体的体积公式可以统一为:
长方体(或正方体)的体积=底面积×高
如果用S表示底面积,体积公式可以写成:
V=Sh
新知讲解
在解决求体积的些实际问题时, 可以直接用它的底面积(或先求出底面积)乘高就可以了。
新知讲解
长方体和正方体不同放置,说法各不相同。
横截面
长
横截面
长
长方体和正方体的侧面叫做横截面。
新知讲解
以长方体为例,说说横截面、长与底面积、高有什么关系呢?
横截面
长
底面积
高
横截面相当于底面积,长相当于高。
长方体(或正方体)的体积=横截面积×长
课堂练习
1.计算。
13= 23= 33= 43= 53=
63= 73= 83= 93= 103=
1
8
27
64
125
216
343
512
729
1000
课堂练习
2.填一填。
长方体 底面积(cm2) 12 30 9
高(cm) 7 12 8
体积(cm3) 96 22.5
84
360
12
2.5
课堂练习
3.一块正方体石料,棱长4分米,如果每立方分米2.7千克,这块石料重多少千克?
4×4×4×2.7
=64×2.7
=172.8(千克)
答:这块石料重172.8千克。
课堂练习
4.一个长方体的横截面是边长为3cm的正方形,它的长是5dm,这个长方体的体积是多少?
5分米=50厘米
3×3×50=450(立方厘米)
答:这个长方形的体积450立方厘米。
课堂练习
4.拓展应用:将一根横截面是10厘米的正方形的长方体木料,沿着横截面截成两段,表面积增加了200平方厘米,若这根木料长为2米,则这根木料的体积是多少立方米?
沿着横截面截成两段,表面积增加了两个面,2个横截面的面积。
10×10×2=200(平方厘米)
200平方厘米=0.02平方米
0.02×2=0.04(立方米)
答:则这根木料的体积是0.04立方米。
课堂总结
通过今天的学习,你有哪些收获?
我会计算长方体和正方体的体积了。
我还知道了长方体和正方体的统一公式。
板书设计
长方体的体积
长方体的体积=长×宽×高
V=a·b·h = abh
正方体的体积=棱长×棱长×棱长
V=a·a·a=a3 (读作:a的立方)
长方体(或正方体)的体积=底面积×高
V=Sh
长方体(或正方体)的体积=横截面积×长
作业布置
完成课本第17、18页“练一练”习题。
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
