全等三角形整章学案
图片预览




文档简介
课题1:11.1全等三角形
教学内容
全等三角形
课时数
1
主备人
吴正平
个性化修改教师
学科
数学
年级
八年级
班级
教学目标
1.理解全等三角形及其对应边、对应角的概念;能准确辨认全等三角形的对应元素.
2.掌握全等三角形的性质;利用全等三角形的性质进行简单的推理和计算,解决实际问题.
教学重点
教学难点
教学方法与资源
教学流程
备注
一、自主学习
P2____P4 内容
1.回忆:举出现实生活中能够完全重合的图形的例子? 同一张底片洗出的同大小照片是能够完全重合的(如图);
2.图形的翻动时
3.将图像平移,之前和之后的图像的特征
想一想,这三组图象中,两个图形的特征是什么?
归纳:这样的能完全重合的图形我们把他们叫做
一个图形经过平移,翻转,旋转后,位置变化了,但 和 都没有改变,那么经过这样的变换后的图形与原来的图形是全等的。
议一议:
你还能说出生活当中全等图形的例子吗?
如果两个图形全等,它们的形状,大小,一定完全相同吗?
二、自主学习,我能行
知识点1:全等三角形
将剪得的两个三角形纸版重合放在一起
(1)将△ABC沿着直线BC平移,得到△DEF
(2)将△ABC沿直线BC翻折,得到△DEF
(3)将△ABC沿点A旋转180度,得到△DEF
观察,△ABC在平移,翻折,旋转后是否发生了改变,各图中的两个三角形是否全等?
能够完全重合的两个三角形叫做 (如下图)。
“全等”用符号“≌”来表示,读作“全等于”,如上图记作△ABC≌△A1B1C1
叫对应顶点,A←→A1,B←→B1,C←→C1
叫对应边,AB←→A1B1,AC←→ , ←→B1C1
叫对应角,∠A←→∠A1,∠B←→∠ ,∠C←→∠
注意:书写全等式时要求把对应顶点字母放在 的位置上
知识点2:全等三角形的性质
全等三角形的性质:全等三角形的 相等, 相等。
用符号表示为
∵△ABC≌△A1B1C1
∴ AB=A1B1, BC=B1C1, AC=A1C1
(全等三角形的 )
∴ ∠ A= ∠ A1, ∠ B= ∠B1 , ∠ C= ∠C1(全等三角形的 )
规律总结
有公共边的,公共边是对应边;有公共角的,公共角是对应角;
有对顶角的,对顶角是对应角.
一对最长的边是对应边,一对最短的边是对应边;
一对最大的角是对应角,一对最小的角是对应角。
三、积极参与,合作探究,我们很棒!
1、如右图△ABC≌ △ADE,若∠D=∠B, ∠C= ∠AED,则
∠DAE= ; ∠DAB= 。
2、判断题
1)全等三角形的对应边相等,对应角相等。( )
2)全等三角形的周长相等,面积也相等。 ( )
3)面积相等的三角形是全等三角形。 ( )
4)周长相等的三角形是全等三角形。 ( )
3、全等用符号 表示,读作: 。
4、若△ BCE ≌ △ CBF,则∠CBE= , ∠BEC= ,BE= , CE= .
5、如图,△ABC≌△AED,AB是△ABC的最大边,AE是△AED的最大边, ∠BAC 与∠ EAD对应角,且∠BAC=25°, ∠B=35°,AB=3cm,BC=1cm,求出∠E,∠ ADE的度数和线段DE,AE 的长度。∠BAD与∠EAC相等吗?为什么?
四、我小结,我积累
五、即时检测,及时过关
1.如图,≌,与,与是对应边,则等于( )
A. B. C. D.
2.如图,≌,和,和分别为对应顶点,若,,,则的长为( )
A.6 B.5 C.4 D.不确定
3.如图,≌,则与相等的角是( )
A. B. C. D.
4.如图,是上的点,≌,则的度数为( )
A. B. C. D.
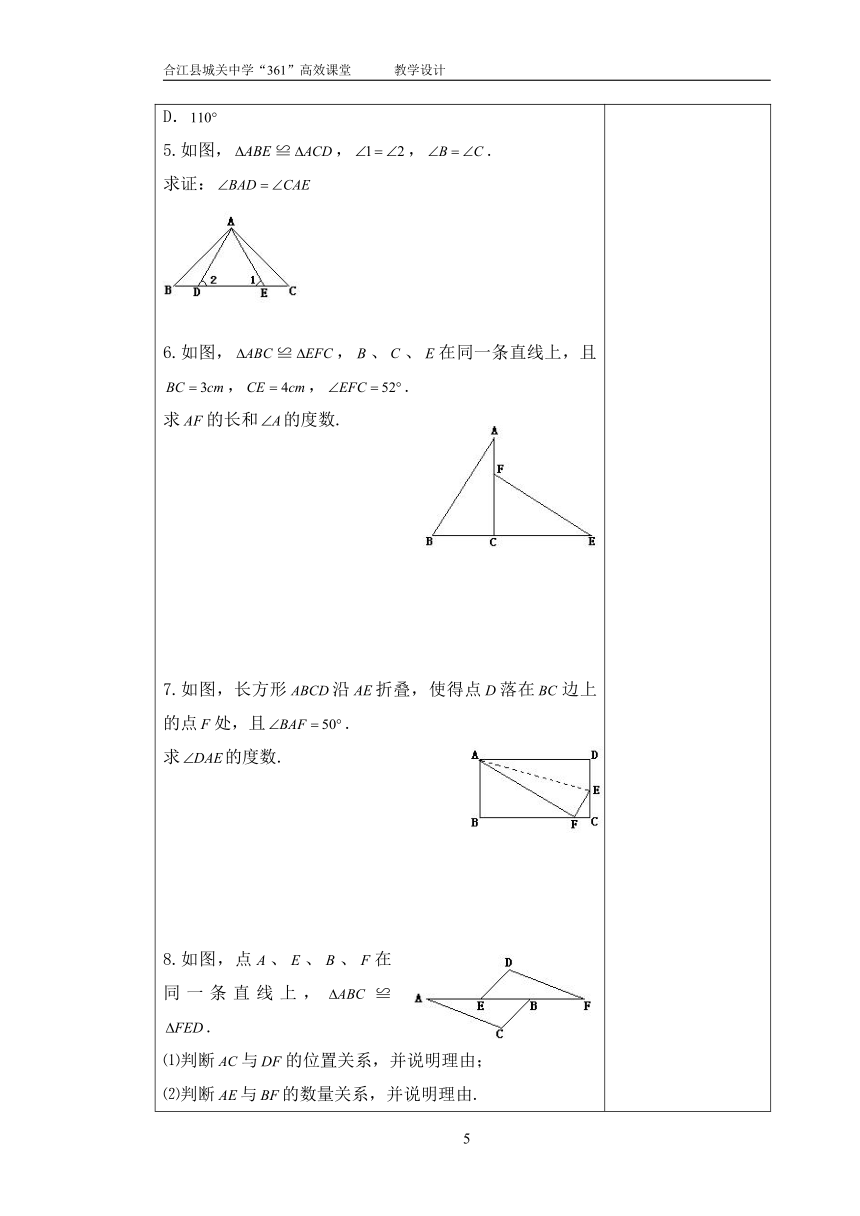
5.如图,≌,,.
求证:
6.如图,≌,、、在同一条直线上,且,,.
求的长和的度数.
7.如图,长方形沿折叠,使得点落在边上的点处,且.
求的度数.
8.如图,点、、、在同一条直线上,≌.
⑴判断与的位置关系,并说明理由;
⑵判断与的数量关系,并说明理由.
9. 如图,≌,,,试判断的形状,并说明理由.
六、我反思,我提高
板书设计
教学反思
课题2:11.2全等三角形的判定(一)
教学内容
全等三角形的判定(一)
课时数
1
主备人
吴正平
个性化修改教师
学科
数学
年级
八年级
班级
教学目标
理解三边对应相等的两个三角形全等的内容.
会运用“边边边”条件证明两个三角形全等
会作一个角等于已知
教学重点
边边边公理证明两个三角形全等
教学难点
用边边边公理解决简单的实际问题
教学方法与资源
教学流程
备注
一、知识回顾
(1)什么叫全等三角形?
(2)全等三角形有什么性质?
2.预习新知
(1)只给一个条件(一组对应边想等或一组对应角相等)画三角形
给一条边:是否可以作三角形?能作出的三角形是否是全等的?
给一个角的度数:能作出的三角形是否是全等的?
(2)给出两个条件
一边一内角
两内角
两边
根据以上的图形大家得出的结论是什么呢?
猜想:如果给出三条边的长度,作出的三角形是全等的吗?
二、自主学习,我能行
知识点1:你会用刻度尺和圆规画△ DEF吗?使其三边分别为3cm,4cm和5cm。
1.画线段EF=3cm
2.分别以E,F为圆心,5cm,4cm长为半径画弧,交于点D。
3.连接DE,DF
4.△ DEF就是我们要求的三角形
再把你画的三角形同其他同学的三角形剪下来进行比较,是否重合?
结论:有三边对应相等的两个三角形全等.
可以简写成 “边边边” 或“ SSS ”
(如图)用数学语言表述为
在△ABC和△ DEF中
三、积极参与,合作探究,我们很棒!
1. 在下列推理中填写需要补充的条件,使结论成立:
如图,在△AOB和△DOC中
∴ △AOB≌△DOC(SSS)
2.如图,AB=CD,AC=BD,△ABC和△DCB是否全等?试说明理由。
3.如图,D、F是线段BC上的两点,AB=EC,AF=ED,要使△ABF≌△ECD ,还需要条件是什么?
,
四、我小结,我积累
五、即时检测,及时过关
1.如图,,,,,则的度数是( )
A.120° B.125° C.127° D.104°
2.如图,线段与交于点,且,,则下面的结论中不正确的是( )
A.≌ B. C. D.
3.在和中,已知,,则补充条件____________,可得到≌.
4.如图,,,、是上两点,且.欲证,可先运用等式的性质证明=________,再用“”证明________≌_________得到结论.
5.如图,在四边形中,,.
求证:①;②.
6.如图,已知,,求证:.
7.如图,与交于点,,、是上两点,且,.
求证:⑴;⑵
8.如图,已知,.求证:.
八、我反思,我提高
板书设计
教学反思
课题3:11.2全等三角形的判定(二)
教学内容
全等三角形的判定(二)
课时数
1
主备人
吴正平
个性化修改教师
学科
数学
年级
八年级
班级
教学目标
1.掌握三角形全等的“SAS”条件,了解三角形的稳定性
2.能运用“SAS”证明简单的三角形全等问题
3.经历探索三角形全等条件的过程,体会利用操作、归纳获得数学结论的过程
教学重点
会运用“边角边”公理证明三角形全等的简单问题
教学难点
分清用两边一角证明三角形相似和全等的不同
教学方法与资源
教学流程
备注
一、知识回顾
三角形全等的判定1: ;
2.两组对应边一组对应角相等是否能证明两个三角形全等呢?
二、自主学习,我能行
问题1:三个角对应相等的两个三角形全等吗?
如图, △ABC和△ADE中,如果 DE∥AB,则∠A=∠A,∠B=∠ADE,∠C= ∠ AED,但△ABC和△ADE不重合,所以不全等。
结论:三个角对应相等的两个三角形_______全等
问题2:
做一做: 先任意出一个画△ABC,再画出一个使AB=3cm,AC=4cm。
这样画出来的三角形与同桌所画的三角形进行比较,它们互相重合吗?
若再加一个条件,使∠A=45°,画出△ABC
画法:
1. 画∠MAN= 45°
2. 在射线AM上截取AB= 3cm
3. 在射线AN上截取AC=4cm
4. 连接BC
把你们所画的三角形剪下来与同桌所画的三角形进行比较,它们能互相重合吗?
1)这两个三角形全等吗?2)你能得到两个三角形全等的判定二吗?
结论:三角形全等的判定2: 和它们的 对应相等的两个三角形全等,简写成 或
问题3:完成课本9例2
以3cm,5cm为三角形的两边,长度为5cm的边所对的角为40° ,情况又怎样?动手画一画,你发现了什么?
比较这两个图形,你能得出三角形全等的判定的条件是
。
注:这个角一定要是这两边所夹的角
练一练,找出各题中全等的三角形
三、积极参与,合作探究,我们很棒!
如图11-2,AB=AD,AC=AE,则可得△ABC≌____其理由是___ ___
11-3
2、如图11-3:已知AB=DC,∠ABC=∠DCB,求证:AC=BD
证明:AB=DC,∠ABC=∠DCB ( )
BC=________( )
∴△BCD≌_______( )
∴AC=________( )
3、如图,已知∠1=∠2,AO=BO,那么△AOP≌△BOP,为什么?
4、如图,AB=AD,AC=AE,∠BAE=∠DAC, △ABC与△ADE全等吗?并说明理由。
四、我小结,我积累
五、即时检测,及时过关
1.如图,AB=DB,BC=BE,欲证△ABC≌△DBC,则需补充的条件是( )
A.∠A=∠D B.∠E=∠C C.∠A=∠C D.∠1=∠2
2.如图:AB=AC,AD=AE,AB⊥AC,AD⊥AE。求证:(1)∠B=∠C,(2)BD=CE
3.如图:CG=CF,BC=DC,AB=ED,点A、B、C、D、E在同一直线上。
求证:(1)AF=EG,(2)BF∥DG。
4.如图,和都是等边三角形,连接、交于.
求证:⑴ ⑵
六、我反思,我提高
板书设计
教学反思
课题4:11.2全等三角形的判定(三)
教学内容
全等三角形的判定(三)
课时数
1
主备人
吴正平
个性化修改教师
学科
数学
年级
八年级
班级
教学目标
会运用“角边角”定理理及其推论证明三角形全等的简单问题
教学重点
灵活运用“角边角”定理理及其推论证明三角形全等
教学难点
运用角边角”定理理及其推论解决简单的问题
教学方法与资源
教学流程
备注
学有准备
在ΔABC和ΔDEF中,已有条件AB=DE,还需添加两个条件才能使≌ΔDEF,不能添加的一组条件是( )
A.∠B=∠E,BC=EF B.BC=EF,AC=DF C.∠A=∠D,BC=EF
问题:添加条件∠A=∠D,∠B=∠E是否也能证明≌ΔDEF呢?
二、自主学习,我能行
探究一
先任意画出一个△ABC,再画一个△A/B/C/,使A/B/=AB,∠A/ =∠A, ∠B/ =∠B 。把画好的△A/B/C/剪下,放到△ABC上,它们全等吗?
画法:1、画A/B/=AB;
2、在 A/B/的同旁画∠DA/ B/ =∠A , ∠EB/A/ =∠B, A/ D,B/E交于点C/。
△A/B/C/就是所要画的三角形。
通过这个实验可以证明什么?
有 和 的两个三角形全等(简写成“角边角”或“ASA”)
探究二
有两个角和其中一个角的对边对应相等的两个三角形是否全等?
如图: 在△ABC和△DEF中,∠A=∠D, ∠B=∠E ,BC=EF,△ABC与△DEF全等吗? 能利用角边角条件证明你的结论吗?
得到的结论是:有 和 的两个三角形全等。(简写成“角角边”或“AAS”)
用符号语言表达为:
证明:在△ABC和△DEF中
∴ △ABC≌△DEF (AAS)
三、积极参与,合作探究
1、下列说法中,正确的是( )
A所有的等腰三角形全等 B有两边对应相等的两个等腰三角形全等
C有一边对应相等的两个等腰三角形全等
D腰和顶角对应相等的两个等腰三角形全等
2、在△ABC与△A′B′C′中,已知∠A=44°,∠B=67°,∠C′=69°,∠A′=44°,且AC=A′C′,那么这两个三角形( )
A 一定不全等 B 一定全等 C 不一定全等
D 以上都不对
3、在△ABC和△DEF中,条件(1)AB=DE,(2)BC=EF,(3)AC=DF,(4) ∠A=∠D,(5) ∠B=∠E,(6) ∠C=∠F,则下列各组条件中,不能保证△ABC≌△DEF的是( )
A(1) (2) (3) B (1) (2) (5) C (1) (3) (5) D(2) (5) (6)
4、如图,AB=DE,AC∥DF,BC∥EF,△ABC与△DEF全等吗?试说明理由.
5、如图,∠1=∠2,∠B=∠D,△ABC和△ADC全等吗?试说明理由。
四、我小结,我积累
五、即时检测,及时过关
1.如图,AB//ED,BC//EF,AF=DC,现在有以下结论:①BC=EF,②连接AE,BD,四边形ABDE是平行四边形,③连BF,CE,四边形BCEF是平行四边形,其中正确的是 (填序号)
2.如图,AB=AC, ,下列结论不成立的是( )
A B
C D ∠BOC=120°
3.如图,在梯形ABCD中,AD//BC,AB=DC,对角线AC与BD交于点O,则图中全等三角形共有( )
1对 B. 2对 C. 3对 D. 4对
4.如图,P为菱形ABCD的对角线的一点,AC平分∠BAD, 于E, 于点F,PF=3cm,试证明P点到AB的距离也是3cm.
5.已知≌,和分别是和边上的高,和相等吗?为什么?
6.如图,已知,,那么,你知道这是为什么吗?
7.已知如图,于点,于点,、交于点,且平分.
⑴图中有多少对全等的三角形?请你一一列举出来(不要求说明理由)
⑵小明说:欲证,可先证明≌得到,再证明≌得到,然后利用等式的性质即可得到,请问他的说法正确吗?如果不正确,请说明理由;如果正确,请按他的思路写出推导过程.
⑶要得到,你还有其他的思路吗?若有,请仿照小明的说法具体说一说你的想法.
八、我反思,我提高
板书设计
教学反思
课题5:11.2全等三角形的判定(四)
教学内容
全等三角形的判定(四)
课时数
1
主备人
吴正平
个性化修改教师
学科
数学
年级
八年级
班级
教学目标
会运用“斜边、直角边(HL)”定理证明三角形全等
教学重点
斜边、直角边(HL)” 证明三角形全等的简单问题
教学难点
了解SSS、SAS、ASA、AAS也适用于直角三角形
教学方法与资源
教学流程
备注
一、学有准备,
我们已经研究了 个证明两个三角形全等的条件,它们分别是 、 、 、 ,注意“ 、 ”是不能证明两个三角形全等的。
二、自主学习,
如图,舞台背景的形状是两个直角三角形,工作人员想知道这两个直角三角形是否全等,但两个三角形都有一条直角边被花盆遮住无法测量.你能帮他想个办法吗?
方法1:用直尺量出斜边AB, A1B1的长度,再用量角器量出其中一个锐角(如∠A与∠A1 )的大小,若它们对应相等,据根( )可以证明两直角三角形是全等的。
方法2:用直尺量出不被遮住的直角边AC, A1C1的长度,再用量角器量出其中一个锐角(如∠A与∠A1 )的大小,若它们对应相等,据根( )可以证明两直角三角形是全等的。
问题:
如果他只带了一个卷尺,能完成这个任务?
那么他只能测直角边和斜边了,只满足斜边和一条直角边对应相等的两个直角三角形能全等吗?
画一画:
任意画一个Rt△ACB ,使∠C﹦90°,再画一个Rt△A′C′B′使∠C﹦∠C′,B′C′﹦BC,A′B′﹦AB
(1):你能试着画出来吗?与小组交流一下。
( 2):把画好的Rt△A′C′B′放到Rt△ACB上
画法:1、画∠MC′N=90°
2、在射线C′M上取B′C′=BC
3、以B′为圆心,AB为半径画弧,交射线C′N于点A′
4、连接A′B′,△A′C′B′就是所作三角形。
它们全等吗?你能发现什么规律?
总结规律
直角三角形全等的判定方法:
_______和一条 对应相等的两个直角三角形全等。简写成“斜边、直角边”或“HL”.
例1:如图,AC⊥BC, BD⊥AD, AC﹦BD,求证:BC﹦AD
证明: 在 Rt△ABC 和 Rt△BAD 中,
∵ AC⊥BC, BD⊥AD
∴∠C与∠D都是直角.
Rt△ABC≌Rt△BAD (HL).
∴ BC﹦AD
三、积极参与,合作探究,
1.两条直角边对应相等的两个直角三角形____,理由是________
2.有一条边和一个锐角对应相等的两个直角三角形_____,理由是____
3.下列叙述的图形中,是全等三角形的只有( )
A 两个含60°角的直角三角形 B 腰对应相等的两个等腰三角形
C 有一边相等的两个等边三角形 D 面积相等的两个直角三角形
4.判断两个三角形全等的方法: (填序号)
(1)三边分别相等的两个三角形全等。
(2)有两边级其夹角对应相等的两个三角形全等。
(3)有两角及其夹边对应相等的两个三角形全等。
(4)有两个角及其中一角的对边对应相等的两个三角形全等。
(5)有一条直角边和斜边对应相等的两个直角三角形全等。
5.如图:CE⊥AB,DF⊥AB,垂足分别为E、F,AC∥DB,且AC=BD,求证:CE=DF
6.如图,AB=CD,DE⊥AC,BF⊥AC,E、F是垂足,DE=BF,求证(1)AE=CF(2)AB∥CD
四、我小结,我积累
五、即时检测,及时过关
1.如图,BA//DC, AB=CE,BC=ED,则AC= ,
2.如图,要测量河两岸相对的两点,的距离,可以在的垂线上取两点,使,再定出的垂线,使在一条直线上,这时测得的的长就是的长,为什么?
3.小明、小敏两人一起做数学作业,小敏把题读到如图8(1)所示,CD⊥AB,BE⊥AC时,还没把题读完,就说:“这题一定是求证∠B=∠C,也太容易了.”她的证法是:由CD⊥AB,BE⊥AC,得∠ADC=∠AEB=90°,公共角∠DAC=∠BAE,所以△DAC≌△EAB.由全等三角形的对应角相等得∠B=∠C.
小明说:“小敏你错了,你未弄清本题的条件和结论,即使有CD⊥AB,BE⊥AC,公共角∠DAC=∠BAE,你的推理也是错误的.看我画的图8(2),显然△DAC与△EAB是不全等的.再说本题不是要证明∠B=∠C,而是要证明BE=CD.”
(1)根据小敏所读的题,判断“∠B=∠C”对吗?她的推理对吗?若不对,请做出正确的推理.
(2)根据小明说的,要证明BE=CD,必然是小敏丢了题中条件,请你把小敏丢的条件找回来,并根据找出的条件,你做出判断BE=CD的正确推理.
(3)要判断三角形全等,从这个问题中你得到了什么启发?
六、我反思,我提高
板书设计
教学反思
课题6:11.3角平分线的性质(第1课时)
教学内容
角平分线的性质(第1课时)
课时数
1
主备人
吴正平
个性化修改教师
学科
数学
年级
八年级
班级
教学目标
1.经历角的平分线性质的发现过程,初步掌握角的平分线的性质定理
2.通过测量操作,发现角的平分线的性质定理
.能用文字语言、符号语言阐述角的平分线的性质定理,提高不同数学语言间的转化能力.
4.能运用角的平分线性质定理解决简单的几何问题.
5.通过合作交流、自主评价,促进良好的学习态度的形成,养成永无止境的科学探索精神.
教学重点
掌握角的平分线的性质定理
教学难点
角平分线定理的应用
教学方法与资源
教学流程
备注
一、学有准备,
自主学习课本P48思考,这是一个平分角的仪器,你能说明它的道理吗?
二、自主学习,我能行
1、我们由上面得探究可以得出作出已知角的平分线的尺规作图的方法
已知:∠AOB
求作:∠AOB的平分线
作法1.以O为圆心,适当长为半径作弧,交OA于M,交OBN于.
2.分别以M,N为圆心.大于MN的长为半径作弧.两弧在∠AOB的内部交于C.
3.作射线OC
则射线OC即为所求
2.在∠AOB的平分线OC上任取一点P,然后,作点P到∠AOB两边的垂线段PD、PE,画一画,量一量,从中你有什么新发现?你能说明其中的道理吗?
角平分线上的点
三、积极参与,合作探究,我们很棒!
如图,OC是∠AOB的平分线,
∵
∴PD=PE
2、在ΔABC中,∠B=90°,AB=7,BC=24,AC=25.(1)ΔABC内是否有一点P到各边的距离都相等?如果有,请作出这一点,并说明理由;(2)求这个距离
在Rt△ABC中,BD平分∠ABC,DE⊥AB于E,则:
⑴图中相等的线段有哪些?相等的角呢?
⑵哪条线段与DE相等?为什么?
⑶若AB=10,BC=8,AC=6,求BE,AE的长和△AED的周长。
在△ABC中,AC⊥BC,AD为∠BAC的平分线,DE⊥AB,AB=7㎝,AC=3㎝,求BE的长
5、已知BE⊥AC于E,CF⊥AB于F,BE、CF相交于D,若BD=CD.求证:AD平分∠BAC
四、我小结,我积累
五、即时检测,及时过关
1.如图(1)所示,∠1=∠2,PD⊥OA,PE⊥OB,垂足分别为D,E,则下列结论中错误的是( ).
A.PD=PE B.OD=OE C.∠DPO=∠EPO D.PD=OD
(1) (2) (3)
2.如图(2)所示,在△ABC中,AB=AC,AD是△ABC的角平分线,DE⊥AB,DF⊥AC,垂足分别是E,F,则下列四个结论:①AD上任意一点到C,B的距离相等;②AD上任意一点到AB,AC的距离相等;③BD=CD,AD⊥BC;④∠BDE=∠CDF,其中正确的个数是( ).
A.1个 B.2个 C.3个 D.4个
3.如图(3)所示,在Rt△ABC中,∠C=90°,AC=BC=1,AB=,AD在∠BAC的平分线上,DE⊥AB于点E,则△DBE的周长为( ).
A.2 B.1+ C. D.无法计算
4.如图所示,AD是∠BAC的平分线,DE⊥AB于E,DF⊥AC于F,且BD=CD,那么BE与CF相等吗?为什么?
5.如图,平分,于,于,连接交于.
求证:
6.如图,,于,于.
⑴求证:在的平分线上;
⑵若将⑴的条件“”和结论“在的平分线上”互换,成立吗?说明理由.
六、我反思,我提高
板书设计
教学反思
课题7:11.3角平分线的性质(第2课时)
教学内容
角平分线的性质(第2课时)
课时数
1
主备人
吴正平
个性化修改教师
学科
数学
年级
八年级
班级
教学目标
进一步熟练掌握角平分线的性质
能用文字语言和符号语言阐述角平分线的逆定理
掌握角平分线逆定理
能运用角平分线的性质和逆定理解决简单的集合问题
教学重点
掌握角平分线的逆定理
教学难点
角平分线的性质和逆定理的应用
教学方法与资源
教学流程
备注
一、学有准备
1.会用尺规作角的平分线及其方法
2.角的平分线的性质:
用数学语言表述:
二、自主学习
思考:反过来,到一个角的两边的距离相等的点是否一定在这个角的平分线上呢?
已知:如图,QD⊥OA,QE⊥OB,
点D、E为垂足,QD=QE.
求证:点Q在∠AOB的平分线上
得到的结论是:
用数学语言表示为:
∵ QD⊥OA,QE⊥OB,QD=QE.
∴点Q在∠AOB的平分线上.
对比角平分线的性质:
角的平分线上的点到角的两边的距离相等.
∵ QD⊥OA,QE⊥OB,点Q在∠AOB的平分线上
∴ QD=QE
三、积极参与,合作探究
如图(1)所示,若在∠AOB内有一点P,PE⊥OA,PF⊥OB,垂足分别为E,F,且PE=PF,则点P在_______,根据是____________.
(2) (3)
2、如图(2):△ABC中,∠C=90°,AC=BC,AD平分∠CAB,交BC于D点,DE⊥AB于点E,且AB=60cm,则△BED的
周长为( )
A 100cm B 80cm C 60cm D 40cm
3.如图(3)所示,DE⊥AB于E,DF⊥AC于点F,若DE=DF,只需添加一个条件,这个条件是__________
4.如图所示,∠AOB=40°,OM平分∠AOB,MA⊥OA于A,MB⊥OB于B,则∠MAB的度数为________
四、我小结,我积累
五、即时检测,及时过关
1.在中,,是的角平分线,若,,则点到的距离为 .
2.的平分线上一点,到的距离为,则到的距离为 .
3.如图,,是的角平分线,,,则点到的距离为 .
4.如图,, 于,于,下列结论错误的是( )
A. B. C. D.
5.三角形中到三边距离相等的点是( )
A.三条边的垂直平分线的交点 B.三条高的交点
C.三条中线的交点 D.三条角平分线的交点
6.如图,中,,,平分交于,于,且,则的周长为( )
A.4 B.6 C.10 D.不能确定
7.如图,,为的角平分线,,连接,则下列结论中不正确的是( )
A. B. C. D.
8.如图, △ABC的角平分线BM,CN相交于点P,求证:点P到三边AB、BC、CA的距离相等
9.如图,已知△ABC的外角∠CBD和∠BCE的平分线相交于点F,
求证:点F在∠DAE的平分线上
10.已知BE⊥AC于E,CF⊥AB于F,BE、CF相交于D,若BD=CD.求证:AD平分∠BAC
11.如图所示,,是中点,平分,判断是否平分,说明理由.
12.已知,如图为的平分线,,点在上,于,于.
求证:
六、我反思,我提高
板书设计
教学反思
课题8:全等三角形复习
教学内容
全等三角形复习
课时数
1
主备人
吴正平
个性化修改教师
学科
数学
年级
八年级
班级
教学目标
教学重点
教学难点
教学方法与资源
教学流程
备注
一、学有准备,胸有成竹
1、全等三角形的性质:
全等三角形的 相等, 相等。
2、全等三角形的判定:
(1)一般三角形全等的判定:
(2)直角三角形全等的判定:
SAS、ASA、AAS、SSS、HL
3、角平分线:
(1)作图
(2)性质定理:
(3)判定定理:
二、自主学习,我能行
(一)、挖掘“隐含条件”判全等
1.如图(1),AB=CD,AC=BD,则与∠ACB相等的角是 ,为什么?
2.如图(2),点D在AB上,点E在AC上,CD与BE相交于点O,且AD=AE,AB=AC.若∠B=20°,CD=5cm,则∠C= ,BE=
3.如图(3),若OB=OD,∠A=∠C,若AB=3cm,则CD=
(二)、熟练转化“间接条件”判全等
1.如图(4)AE=CF,∠AFD=∠CEB,DF=BE,△AFD与△ CEB全等吗?为什么?
2.如图(5)∠CAE=∠BAD,∠B=∠D,AC=AE,△ABC与△ADE全等吗?为什么?
3.“三月三,放风筝”如图(6)是小东同学自己做的风筝,他根据AB=AD,BC=DC,不用度量,就知道∠ABC=∠ADC。请用所学的知识给予说明。
(三)、体验感受条件开放题
1.填空:如图请你选择适合的条件填入空格中,使两个三角形全等。
①因为DF=DF, , ,根据 , 可知△DEF≌△DGF。
②因为DF=DF, , ,根据 , 可知△DEF≌△DGF。
③因为DF=DF, , ,根 据 , 可知△DEF≌△DGF。
④因为DF=DF, , ,根据 , 可知△DEF≌△DGF
(四)、体验感受结论开放题
1.如图(8),△ABE≌△ACD,由此你能得到什么结论?(越多越好)
三、我小结,我积累
四、即时检测,及时过关
1、如图,在△ABC 中,AD⊥ BC,CE⊥ AB,垂足分别为D、E,AD、CE交于点H,请你添加一个适当的条件: ,使△AEH≌△CEB。
2、如图,CD、BE相交于点A,M是BC的中点,∠DMB=∠EMC,∠EBC=∠CMD,
求证:△BMD≌△CME
3、如图,在△ABC中,BE是角平分线,AD⊥BE,垂足为D,求证:∠BAD=∠DAE+∠C
如图,A,B,C三点在同一直线上,分别以AB,BC为边在AC同侧作等边△ABD和等边△BCE,AE交BD于点F,DC交BE于点G,(1) AE与DC相等吗? (2)BF与BG相等吗?
4、如图,在△ABC中,AB﹥AC,∠BAD=∠CAD,P为AD上任意一点。
求证:AB-AC﹥PB-PC。
5、如图,在△ABC中,AC=BC,在△DEC中,CD=CE,且∠DCE=∠ACB,AD与BE相交于点P,求证:PC平分∠BPD
6、如图,在四边形ABCD中,已知AB=CD,AD=CB,DE=BF,且点E、F分别在AD、CB的延长线上,求证:BE=DF
六、我反思,我提高
板书设计
教学反思
教学内容
全等三角形
课时数
1
主备人
吴正平
个性化修改教师
学科
数学
年级
八年级
班级
教学目标
1.理解全等三角形及其对应边、对应角的概念;能准确辨认全等三角形的对应元素.
2.掌握全等三角形的性质;利用全等三角形的性质进行简单的推理和计算,解决实际问题.
教学重点
教学难点
教学方法与资源
教学流程
备注
一、自主学习
P2____P4 内容
1.回忆:举出现实生活中能够完全重合的图形的例子? 同一张底片洗出的同大小照片是能够完全重合的(如图);
2.图形的翻动时
3.将图像平移,之前和之后的图像的特征
想一想,这三组图象中,两个图形的特征是什么?
归纳:这样的能完全重合的图形我们把他们叫做
一个图形经过平移,翻转,旋转后,位置变化了,但 和 都没有改变,那么经过这样的变换后的图形与原来的图形是全等的。
议一议:
你还能说出生活当中全等图形的例子吗?
如果两个图形全等,它们的形状,大小,一定完全相同吗?
二、自主学习,我能行
知识点1:全等三角形
将剪得的两个三角形纸版重合放在一起
(1)将△ABC沿着直线BC平移,得到△DEF
(2)将△ABC沿直线BC翻折,得到△DEF
(3)将△ABC沿点A旋转180度,得到△DEF
观察,△ABC在平移,翻折,旋转后是否发生了改变,各图中的两个三角形是否全等?
能够完全重合的两个三角形叫做 (如下图)。
“全等”用符号“≌”来表示,读作“全等于”,如上图记作△ABC≌△A1B1C1
叫对应顶点,A←→A1,B←→B1,C←→C1
叫对应边,AB←→A1B1,AC←→ , ←→B1C1
叫对应角,∠A←→∠A1,∠B←→∠ ,∠C←→∠
注意:书写全等式时要求把对应顶点字母放在 的位置上
知识点2:全等三角形的性质
全等三角形的性质:全等三角形的 相等, 相等。
用符号表示为
∵△ABC≌△A1B1C1
∴ AB=A1B1, BC=B1C1, AC=A1C1
(全等三角形的 )
∴ ∠ A= ∠ A1, ∠ B= ∠B1 , ∠ C= ∠C1(全等三角形的 )
规律总结
有公共边的,公共边是对应边;有公共角的,公共角是对应角;
有对顶角的,对顶角是对应角.
一对最长的边是对应边,一对最短的边是对应边;
一对最大的角是对应角,一对最小的角是对应角。
三、积极参与,合作探究,我们很棒!
1、如右图△ABC≌ △ADE,若∠D=∠B, ∠C= ∠AED,则
∠DAE= ; ∠DAB= 。
2、判断题
1)全等三角形的对应边相等,对应角相等。( )
2)全等三角形的周长相等,面积也相等。 ( )
3)面积相等的三角形是全等三角形。 ( )
4)周长相等的三角形是全等三角形。 ( )
3、全等用符号 表示,读作: 。
4、若△ BCE ≌ △ CBF,则∠CBE= , ∠BEC= ,BE= , CE= .
5、如图,△ABC≌△AED,AB是△ABC的最大边,AE是△AED的最大边, ∠BAC 与∠ EAD对应角,且∠BAC=25°, ∠B=35°,AB=3cm,BC=1cm,求出∠E,∠ ADE的度数和线段DE,AE 的长度。∠BAD与∠EAC相等吗?为什么?
四、我小结,我积累
五、即时检测,及时过关
1.如图,≌,与,与是对应边,则等于( )
A. B. C. D.
2.如图,≌,和,和分别为对应顶点,若,,,则的长为( )
A.6 B.5 C.4 D.不确定
3.如图,≌,则与相等的角是( )
A. B. C. D.
4.如图,是上的点,≌,则的度数为( )
A. B. C. D.
5.如图,≌,,.
求证:
6.如图,≌,、、在同一条直线上,且,,.
求的长和的度数.
7.如图,长方形沿折叠,使得点落在边上的点处,且.
求的度数.
8.如图,点、、、在同一条直线上,≌.
⑴判断与的位置关系,并说明理由;
⑵判断与的数量关系,并说明理由.
9. 如图,≌,,,试判断的形状,并说明理由.
六、我反思,我提高
板书设计
教学反思
课题2:11.2全等三角形的判定(一)
教学内容
全等三角形的判定(一)
课时数
1
主备人
吴正平
个性化修改教师
学科
数学
年级
八年级
班级
教学目标
理解三边对应相等的两个三角形全等的内容.
会运用“边边边”条件证明两个三角形全等
会作一个角等于已知
教学重点
边边边公理证明两个三角形全等
教学难点
用边边边公理解决简单的实际问题
教学方法与资源
教学流程
备注
一、知识回顾
(1)什么叫全等三角形?
(2)全等三角形有什么性质?
2.预习新知
(1)只给一个条件(一组对应边想等或一组对应角相等)画三角形
给一条边:是否可以作三角形?能作出的三角形是否是全等的?
给一个角的度数:能作出的三角形是否是全等的?
(2)给出两个条件
一边一内角
两内角
两边
根据以上的图形大家得出的结论是什么呢?
猜想:如果给出三条边的长度,作出的三角形是全等的吗?
二、自主学习,我能行
知识点1:你会用刻度尺和圆规画△ DEF吗?使其三边分别为3cm,4cm和5cm。
1.画线段EF=3cm
2.分别以E,F为圆心,5cm,4cm长为半径画弧,交于点D。
3.连接DE,DF
4.△ DEF就是我们要求的三角形
再把你画的三角形同其他同学的三角形剪下来进行比较,是否重合?
结论:有三边对应相等的两个三角形全等.
可以简写成 “边边边” 或“ SSS ”
(如图)用数学语言表述为
在△ABC和△ DEF中
三、积极参与,合作探究,我们很棒!
1. 在下列推理中填写需要补充的条件,使结论成立:
如图,在△AOB和△DOC中
∴ △AOB≌△DOC(SSS)
2.如图,AB=CD,AC=BD,△ABC和△DCB是否全等?试说明理由。
3.如图,D、F是线段BC上的两点,AB=EC,AF=ED,要使△ABF≌△ECD ,还需要条件是什么?
,
四、我小结,我积累
五、即时检测,及时过关
1.如图,,,,,则的度数是( )
A.120° B.125° C.127° D.104°
2.如图,线段与交于点,且,,则下面的结论中不正确的是( )
A.≌ B. C. D.
3.在和中,已知,,则补充条件____________,可得到≌.
4.如图,,,、是上两点,且.欲证,可先运用等式的性质证明=________,再用“”证明________≌_________得到结论.
5.如图,在四边形中,,.
求证:①;②.
6.如图,已知,,求证:.
7.如图,与交于点,,、是上两点,且,.
求证:⑴;⑵
8.如图,已知,.求证:.
八、我反思,我提高
板书设计
教学反思
课题3:11.2全等三角形的判定(二)
教学内容
全等三角形的判定(二)
课时数
1
主备人
吴正平
个性化修改教师
学科
数学
年级
八年级
班级
教学目标
1.掌握三角形全等的“SAS”条件,了解三角形的稳定性
2.能运用“SAS”证明简单的三角形全等问题
3.经历探索三角形全等条件的过程,体会利用操作、归纳获得数学结论的过程
教学重点
会运用“边角边”公理证明三角形全等的简单问题
教学难点
分清用两边一角证明三角形相似和全等的不同
教学方法与资源
教学流程
备注
一、知识回顾
三角形全等的判定1: ;
2.两组对应边一组对应角相等是否能证明两个三角形全等呢?
二、自主学习,我能行
问题1:三个角对应相等的两个三角形全等吗?
如图, △ABC和△ADE中,如果 DE∥AB,则∠A=∠A,∠B=∠ADE,∠C= ∠ AED,但△ABC和△ADE不重合,所以不全等。
结论:三个角对应相等的两个三角形_______全等
问题2:
做一做: 先任意出一个画△ABC,再画出一个使AB=3cm,AC=4cm。
这样画出来的三角形与同桌所画的三角形进行比较,它们互相重合吗?
若再加一个条件,使∠A=45°,画出△ABC
画法:
1. 画∠MAN= 45°
2. 在射线AM上截取AB= 3cm
3. 在射线AN上截取AC=4cm
4. 连接BC
把你们所画的三角形剪下来与同桌所画的三角形进行比较,它们能互相重合吗?
1)这两个三角形全等吗?2)你能得到两个三角形全等的判定二吗?
结论:三角形全等的判定2: 和它们的 对应相等的两个三角形全等,简写成 或
问题3:完成课本9例2
以3cm,5cm为三角形的两边,长度为5cm的边所对的角为40° ,情况又怎样?动手画一画,你发现了什么?
比较这两个图形,你能得出三角形全等的判定的条件是
。
注:这个角一定要是这两边所夹的角
练一练,找出各题中全等的三角形
三、积极参与,合作探究,我们很棒!
如图11-2,AB=AD,AC=AE,则可得△ABC≌____其理由是___ ___
11-3
2、如图11-3:已知AB=DC,∠ABC=∠DCB,求证:AC=BD
证明:AB=DC,∠ABC=∠DCB ( )
BC=________( )
∴△BCD≌_______( )
∴AC=________( )
3、如图,已知∠1=∠2,AO=BO,那么△AOP≌△BOP,为什么?
4、如图,AB=AD,AC=AE,∠BAE=∠DAC, △ABC与△ADE全等吗?并说明理由。
四、我小结,我积累
五、即时检测,及时过关
1.如图,AB=DB,BC=BE,欲证△ABC≌△DBC,则需补充的条件是( )
A.∠A=∠D B.∠E=∠C C.∠A=∠C D.∠1=∠2
2.如图:AB=AC,AD=AE,AB⊥AC,AD⊥AE。求证:(1)∠B=∠C,(2)BD=CE
3.如图:CG=CF,BC=DC,AB=ED,点A、B、C、D、E在同一直线上。
求证:(1)AF=EG,(2)BF∥DG。
4.如图,和都是等边三角形,连接、交于.
求证:⑴ ⑵
六、我反思,我提高
板书设计
教学反思
课题4:11.2全等三角形的判定(三)
教学内容
全等三角形的判定(三)
课时数
1
主备人
吴正平
个性化修改教师
学科
数学
年级
八年级
班级
教学目标
会运用“角边角”定理理及其推论证明三角形全等的简单问题
教学重点
灵活运用“角边角”定理理及其推论证明三角形全等
教学难点
运用角边角”定理理及其推论解决简单的问题
教学方法与资源
教学流程
备注
学有准备
在ΔABC和ΔDEF中,已有条件AB=DE,还需添加两个条件才能使≌ΔDEF,不能添加的一组条件是( )
A.∠B=∠E,BC=EF B.BC=EF,AC=DF C.∠A=∠D,BC=EF
问题:添加条件∠A=∠D,∠B=∠E是否也能证明≌ΔDEF呢?
二、自主学习,我能行
探究一
先任意画出一个△ABC,再画一个△A/B/C/,使A/B/=AB,∠A/ =∠A, ∠B/ =∠B 。把画好的△A/B/C/剪下,放到△ABC上,它们全等吗?
画法:1、画A/B/=AB;
2、在 A/B/的同旁画∠DA/ B/ =∠A , ∠EB/A/ =∠B, A/ D,B/E交于点C/。
△A/B/C/就是所要画的三角形。
通过这个实验可以证明什么?
有 和 的两个三角形全等(简写成“角边角”或“ASA”)
探究二
有两个角和其中一个角的对边对应相等的两个三角形是否全等?
如图: 在△ABC和△DEF中,∠A=∠D, ∠B=∠E ,BC=EF,△ABC与△DEF全等吗? 能利用角边角条件证明你的结论吗?
得到的结论是:有 和 的两个三角形全等。(简写成“角角边”或“AAS”)
用符号语言表达为:
证明:在△ABC和△DEF中
∴ △ABC≌△DEF (AAS)
三、积极参与,合作探究
1、下列说法中,正确的是( )
A所有的等腰三角形全等 B有两边对应相等的两个等腰三角形全等
C有一边对应相等的两个等腰三角形全等
D腰和顶角对应相等的两个等腰三角形全等
2、在△ABC与△A′B′C′中,已知∠A=44°,∠B=67°,∠C′=69°,∠A′=44°,且AC=A′C′,那么这两个三角形( )
A 一定不全等 B 一定全等 C 不一定全等
D 以上都不对
3、在△ABC和△DEF中,条件(1)AB=DE,(2)BC=EF,(3)AC=DF,(4) ∠A=∠D,(5) ∠B=∠E,(6) ∠C=∠F,则下列各组条件中,不能保证△ABC≌△DEF的是( )
A(1) (2) (3) B (1) (2) (5) C (1) (3) (5) D(2) (5) (6)
4、如图,AB=DE,AC∥DF,BC∥EF,△ABC与△DEF全等吗?试说明理由.
5、如图,∠1=∠2,∠B=∠D,△ABC和△ADC全等吗?试说明理由。
四、我小结,我积累
五、即时检测,及时过关
1.如图,AB//ED,BC//EF,AF=DC,现在有以下结论:①BC=EF,②连接AE,BD,四边形ABDE是平行四边形,③连BF,CE,四边形BCEF是平行四边形,其中正确的是 (填序号)
2.如图,AB=AC, ,下列结论不成立的是( )
A B
C D ∠BOC=120°
3.如图,在梯形ABCD中,AD//BC,AB=DC,对角线AC与BD交于点O,则图中全等三角形共有( )
1对 B. 2对 C. 3对 D. 4对
4.如图,P为菱形ABCD的对角线的一点,AC平分∠BAD, 于E, 于点F,PF=3cm,试证明P点到AB的距离也是3cm.
5.已知≌,和分别是和边上的高,和相等吗?为什么?
6.如图,已知,,那么,你知道这是为什么吗?
7.已知如图,于点,于点,、交于点,且平分.
⑴图中有多少对全等的三角形?请你一一列举出来(不要求说明理由)
⑵小明说:欲证,可先证明≌得到,再证明≌得到,然后利用等式的性质即可得到,请问他的说法正确吗?如果不正确,请说明理由;如果正确,请按他的思路写出推导过程.
⑶要得到,你还有其他的思路吗?若有,请仿照小明的说法具体说一说你的想法.
八、我反思,我提高
板书设计
教学反思
课题5:11.2全等三角形的判定(四)
教学内容
全等三角形的判定(四)
课时数
1
主备人
吴正平
个性化修改教师
学科
数学
年级
八年级
班级
教学目标
会运用“斜边、直角边(HL)”定理证明三角形全等
教学重点
斜边、直角边(HL)” 证明三角形全等的简单问题
教学难点
了解SSS、SAS、ASA、AAS也适用于直角三角形
教学方法与资源
教学流程
备注
一、学有准备,
我们已经研究了 个证明两个三角形全等的条件,它们分别是 、 、 、 ,注意“ 、 ”是不能证明两个三角形全等的。
二、自主学习,
如图,舞台背景的形状是两个直角三角形,工作人员想知道这两个直角三角形是否全等,但两个三角形都有一条直角边被花盆遮住无法测量.你能帮他想个办法吗?
方法1:用直尺量出斜边AB, A1B1的长度,再用量角器量出其中一个锐角(如∠A与∠A1 )的大小,若它们对应相等,据根( )可以证明两直角三角形是全等的。
方法2:用直尺量出不被遮住的直角边AC, A1C1的长度,再用量角器量出其中一个锐角(如∠A与∠A1 )的大小,若它们对应相等,据根( )可以证明两直角三角形是全等的。
问题:
如果他只带了一个卷尺,能完成这个任务?
那么他只能测直角边和斜边了,只满足斜边和一条直角边对应相等的两个直角三角形能全等吗?
画一画:
任意画一个Rt△ACB ,使∠C﹦90°,再画一个Rt△A′C′B′使∠C﹦∠C′,B′C′﹦BC,A′B′﹦AB
(1):你能试着画出来吗?与小组交流一下。
( 2):把画好的Rt△A′C′B′放到Rt△ACB上
画法:1、画∠MC′N=90°
2、在射线C′M上取B′C′=BC
3、以B′为圆心,AB为半径画弧,交射线C′N于点A′
4、连接A′B′,△A′C′B′就是所作三角形。
它们全等吗?你能发现什么规律?
总结规律
直角三角形全等的判定方法:
_______和一条 对应相等的两个直角三角形全等。简写成“斜边、直角边”或“HL”.
例1:如图,AC⊥BC, BD⊥AD, AC﹦BD,求证:BC﹦AD
证明: 在 Rt△ABC 和 Rt△BAD 中,
∵ AC⊥BC, BD⊥AD
∴∠C与∠D都是直角.
Rt△ABC≌Rt△BAD (HL).
∴ BC﹦AD
三、积极参与,合作探究,
1.两条直角边对应相等的两个直角三角形____,理由是________
2.有一条边和一个锐角对应相等的两个直角三角形_____,理由是____
3.下列叙述的图形中,是全等三角形的只有( )
A 两个含60°角的直角三角形 B 腰对应相等的两个等腰三角形
C 有一边相等的两个等边三角形 D 面积相等的两个直角三角形
4.判断两个三角形全等的方法: (填序号)
(1)三边分别相等的两个三角形全等。
(2)有两边级其夹角对应相等的两个三角形全等。
(3)有两角及其夹边对应相等的两个三角形全等。
(4)有两个角及其中一角的对边对应相等的两个三角形全等。
(5)有一条直角边和斜边对应相等的两个直角三角形全等。
5.如图:CE⊥AB,DF⊥AB,垂足分别为E、F,AC∥DB,且AC=BD,求证:CE=DF
6.如图,AB=CD,DE⊥AC,BF⊥AC,E、F是垂足,DE=BF,求证(1)AE=CF(2)AB∥CD
四、我小结,我积累
五、即时检测,及时过关
1.如图,BA//DC, AB=CE,BC=ED,则AC= ,
2.如图,要测量河两岸相对的两点,的距离,可以在的垂线上取两点,使,再定出的垂线,使在一条直线上,这时测得的的长就是的长,为什么?
3.小明、小敏两人一起做数学作业,小敏把题读到如图8(1)所示,CD⊥AB,BE⊥AC时,还没把题读完,就说:“这题一定是求证∠B=∠C,也太容易了.”她的证法是:由CD⊥AB,BE⊥AC,得∠ADC=∠AEB=90°,公共角∠DAC=∠BAE,所以△DAC≌△EAB.由全等三角形的对应角相等得∠B=∠C.
小明说:“小敏你错了,你未弄清本题的条件和结论,即使有CD⊥AB,BE⊥AC,公共角∠DAC=∠BAE,你的推理也是错误的.看我画的图8(2),显然△DAC与△EAB是不全等的.再说本题不是要证明∠B=∠C,而是要证明BE=CD.”
(1)根据小敏所读的题,判断“∠B=∠C”对吗?她的推理对吗?若不对,请做出正确的推理.
(2)根据小明说的,要证明BE=CD,必然是小敏丢了题中条件,请你把小敏丢的条件找回来,并根据找出的条件,你做出判断BE=CD的正确推理.
(3)要判断三角形全等,从这个问题中你得到了什么启发?
六、我反思,我提高
板书设计
教学反思
课题6:11.3角平分线的性质(第1课时)
教学内容
角平分线的性质(第1课时)
课时数
1
主备人
吴正平
个性化修改教师
学科
数学
年级
八年级
班级
教学目标
1.经历角的平分线性质的发现过程,初步掌握角的平分线的性质定理
2.通过测量操作,发现角的平分线的性质定理
.能用文字语言、符号语言阐述角的平分线的性质定理,提高不同数学语言间的转化能力.
4.能运用角的平分线性质定理解决简单的几何问题.
5.通过合作交流、自主评价,促进良好的学习态度的形成,养成永无止境的科学探索精神.
教学重点
掌握角的平分线的性质定理
教学难点
角平分线定理的应用
教学方法与资源
教学流程
备注
一、学有准备,
自主学习课本P48思考,这是一个平分角的仪器,你能说明它的道理吗?
二、自主学习,我能行
1、我们由上面得探究可以得出作出已知角的平分线的尺规作图的方法
已知:∠AOB
求作:∠AOB的平分线
作法1.以O为圆心,适当长为半径作弧,交OA于M,交OBN于.
2.分别以M,N为圆心.大于MN的长为半径作弧.两弧在∠AOB的内部交于C.
3.作射线OC
则射线OC即为所求
2.在∠AOB的平分线OC上任取一点P,然后,作点P到∠AOB两边的垂线段PD、PE,画一画,量一量,从中你有什么新发现?你能说明其中的道理吗?
角平分线上的点
三、积极参与,合作探究,我们很棒!
如图,OC是∠AOB的平分线,
∵
∴PD=PE
2、在ΔABC中,∠B=90°,AB=7,BC=24,AC=25.(1)ΔABC内是否有一点P到各边的距离都相等?如果有,请作出这一点,并说明理由;(2)求这个距离
在Rt△ABC中,BD平分∠ABC,DE⊥AB于E,则:
⑴图中相等的线段有哪些?相等的角呢?
⑵哪条线段与DE相等?为什么?
⑶若AB=10,BC=8,AC=6,求BE,AE的长和△AED的周长。
在△ABC中,AC⊥BC,AD为∠BAC的平分线,DE⊥AB,AB=7㎝,AC=3㎝,求BE的长
5、已知BE⊥AC于E,CF⊥AB于F,BE、CF相交于D,若BD=CD.求证:AD平分∠BAC
四、我小结,我积累
五、即时检测,及时过关
1.如图(1)所示,∠1=∠2,PD⊥OA,PE⊥OB,垂足分别为D,E,则下列结论中错误的是( ).
A.PD=PE B.OD=OE C.∠DPO=∠EPO D.PD=OD
(1) (2) (3)
2.如图(2)所示,在△ABC中,AB=AC,AD是△ABC的角平分线,DE⊥AB,DF⊥AC,垂足分别是E,F,则下列四个结论:①AD上任意一点到C,B的距离相等;②AD上任意一点到AB,AC的距离相等;③BD=CD,AD⊥BC;④∠BDE=∠CDF,其中正确的个数是( ).
A.1个 B.2个 C.3个 D.4个
3.如图(3)所示,在Rt△ABC中,∠C=90°,AC=BC=1,AB=,AD在∠BAC的平分线上,DE⊥AB于点E,则△DBE的周长为( ).
A.2 B.1+ C. D.无法计算
4.如图所示,AD是∠BAC的平分线,DE⊥AB于E,DF⊥AC于F,且BD=CD,那么BE与CF相等吗?为什么?
5.如图,平分,于,于,连接交于.
求证:
6.如图,,于,于.
⑴求证:在的平分线上;
⑵若将⑴的条件“”和结论“在的平分线上”互换,成立吗?说明理由.
六、我反思,我提高
板书设计
教学反思
课题7:11.3角平分线的性质(第2课时)
教学内容
角平分线的性质(第2课时)
课时数
1
主备人
吴正平
个性化修改教师
学科
数学
年级
八年级
班级
教学目标
进一步熟练掌握角平分线的性质
能用文字语言和符号语言阐述角平分线的逆定理
掌握角平分线逆定理
能运用角平分线的性质和逆定理解决简单的集合问题
教学重点
掌握角平分线的逆定理
教学难点
角平分线的性质和逆定理的应用
教学方法与资源
教学流程
备注
一、学有准备
1.会用尺规作角的平分线及其方法
2.角的平分线的性质:
用数学语言表述:
二、自主学习
思考:反过来,到一个角的两边的距离相等的点是否一定在这个角的平分线上呢?
已知:如图,QD⊥OA,QE⊥OB,
点D、E为垂足,QD=QE.
求证:点Q在∠AOB的平分线上
得到的结论是:
用数学语言表示为:
∵ QD⊥OA,QE⊥OB,QD=QE.
∴点Q在∠AOB的平分线上.
对比角平分线的性质:
角的平分线上的点到角的两边的距离相等.
∵ QD⊥OA,QE⊥OB,点Q在∠AOB的平分线上
∴ QD=QE
三、积极参与,合作探究
如图(1)所示,若在∠AOB内有一点P,PE⊥OA,PF⊥OB,垂足分别为E,F,且PE=PF,则点P在_______,根据是____________.
(2) (3)
2、如图(2):△ABC中,∠C=90°,AC=BC,AD平分∠CAB,交BC于D点,DE⊥AB于点E,且AB=60cm,则△BED的
周长为( )
A 100cm B 80cm C 60cm D 40cm
3.如图(3)所示,DE⊥AB于E,DF⊥AC于点F,若DE=DF,只需添加一个条件,这个条件是__________
4.如图所示,∠AOB=40°,OM平分∠AOB,MA⊥OA于A,MB⊥OB于B,则∠MAB的度数为________
四、我小结,我积累
五、即时检测,及时过关
1.在中,,是的角平分线,若,,则点到的距离为 .
2.的平分线上一点,到的距离为,则到的距离为 .
3.如图,,是的角平分线,,,则点到的距离为 .
4.如图,, 于,于,下列结论错误的是( )
A. B. C. D.
5.三角形中到三边距离相等的点是( )
A.三条边的垂直平分线的交点 B.三条高的交点
C.三条中线的交点 D.三条角平分线的交点
6.如图,中,,,平分交于,于,且,则的周长为( )
A.4 B.6 C.10 D.不能确定
7.如图,,为的角平分线,,连接,则下列结论中不正确的是( )
A. B. C. D.
8.如图, △ABC的角平分线BM,CN相交于点P,求证:点P到三边AB、BC、CA的距离相等
9.如图,已知△ABC的外角∠CBD和∠BCE的平分线相交于点F,
求证:点F在∠DAE的平分线上
10.已知BE⊥AC于E,CF⊥AB于F,BE、CF相交于D,若BD=CD.求证:AD平分∠BAC
11.如图所示,,是中点,平分,判断是否平分,说明理由.
12.已知,如图为的平分线,,点在上,于,于.
求证:
六、我反思,我提高
板书设计
教学反思
课题8:全等三角形复习
教学内容
全等三角形复习
课时数
1
主备人
吴正平
个性化修改教师
学科
数学
年级
八年级
班级
教学目标
教学重点
教学难点
教学方法与资源
教学流程
备注
一、学有准备,胸有成竹
1、全等三角形的性质:
全等三角形的 相等, 相等。
2、全等三角形的判定:
(1)一般三角形全等的判定:
(2)直角三角形全等的判定:
SAS、ASA、AAS、SSS、HL
3、角平分线:
(1)作图
(2)性质定理:
(3)判定定理:
二、自主学习,我能行
(一)、挖掘“隐含条件”判全等
1.如图(1),AB=CD,AC=BD,则与∠ACB相等的角是 ,为什么?
2.如图(2),点D在AB上,点E在AC上,CD与BE相交于点O,且AD=AE,AB=AC.若∠B=20°,CD=5cm,则∠C= ,BE=
3.如图(3),若OB=OD,∠A=∠C,若AB=3cm,则CD=
(二)、熟练转化“间接条件”判全等
1.如图(4)AE=CF,∠AFD=∠CEB,DF=BE,△AFD与△ CEB全等吗?为什么?
2.如图(5)∠CAE=∠BAD,∠B=∠D,AC=AE,△ABC与△ADE全等吗?为什么?
3.“三月三,放风筝”如图(6)是小东同学自己做的风筝,他根据AB=AD,BC=DC,不用度量,就知道∠ABC=∠ADC。请用所学的知识给予说明。
(三)、体验感受条件开放题
1.填空:如图请你选择适合的条件填入空格中,使两个三角形全等。
①因为DF=DF, , ,根据 , 可知△DEF≌△DGF。
②因为DF=DF, , ,根据 , 可知△DEF≌△DGF。
③因为DF=DF, , ,根 据 , 可知△DEF≌△DGF。
④因为DF=DF, , ,根据 , 可知△DEF≌△DGF
(四)、体验感受结论开放题
1.如图(8),△ABE≌△ACD,由此你能得到什么结论?(越多越好)
三、我小结,我积累
四、即时检测,及时过关
1、如图,在△ABC 中,AD⊥ BC,CE⊥ AB,垂足分别为D、E,AD、CE交于点H,请你添加一个适当的条件: ,使△AEH≌△CEB。
2、如图,CD、BE相交于点A,M是BC的中点,∠DMB=∠EMC,∠EBC=∠CMD,
求证:△BMD≌△CME
3、如图,在△ABC中,BE是角平分线,AD⊥BE,垂足为D,求证:∠BAD=∠DAE+∠C
如图,A,B,C三点在同一直线上,分别以AB,BC为边在AC同侧作等边△ABD和等边△BCE,AE交BD于点F,DC交BE于点G,(1) AE与DC相等吗? (2)BF与BG相等吗?
4、如图,在△ABC中,AB﹥AC,∠BAD=∠CAD,P为AD上任意一点。
求证:AB-AC﹥PB-PC。
5、如图,在△ABC中,AC=BC,在△DEC中,CD=CE,且∠DCE=∠ACB,AD与BE相交于点P,求证:PC平分∠BPD
6、如图,在四边形ABCD中,已知AB=CD,AD=CB,DE=BF,且点E、F分别在AD、CB的延长线上,求证:BE=DF
六、我反思,我提高
板书设计
教学反思
