4.5 角的比较与补(余)角 学案(无答案)
文档属性
| 名称 | 4.5 角的比较与补(余)角 学案(无答案) |  | |
| 格式 | doc | ||
| 文件大小 | 543.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-17 17:57:06 | ||
图片预览


文档简介
第4章 直线与角
4.5 角的比较与补(余)角
学案一
学习目标:
1. 会用叠合法和度量法比较两个角的大小。
2.了解角平分线的概念,并会平分一个角。
3.了解角的和差的意义,并进行角的简单计算。
教学重点:角的大小比较。
教学难点:角的和差计算。
一、学前准备
(1)、上节课我们一起研究了“角”的几何图形,什么是“角”,几何上是如何下定义的呢?
(2)、试一试,用不同的方法表示下列各角?
(3)、能比较上述角的大小吗?如果能,试阐述你的方法?
二、探究新知
活动1:
(1) 请同学们同桌分别画两个角,然后交换用量角器测量其度数,比较它们的大小.
(2)比一比,你和其他同学画的角的度数一样吗?可否把角从角度数的大小来划分,应该这样进行分类?
小结:角的分类
活动2:
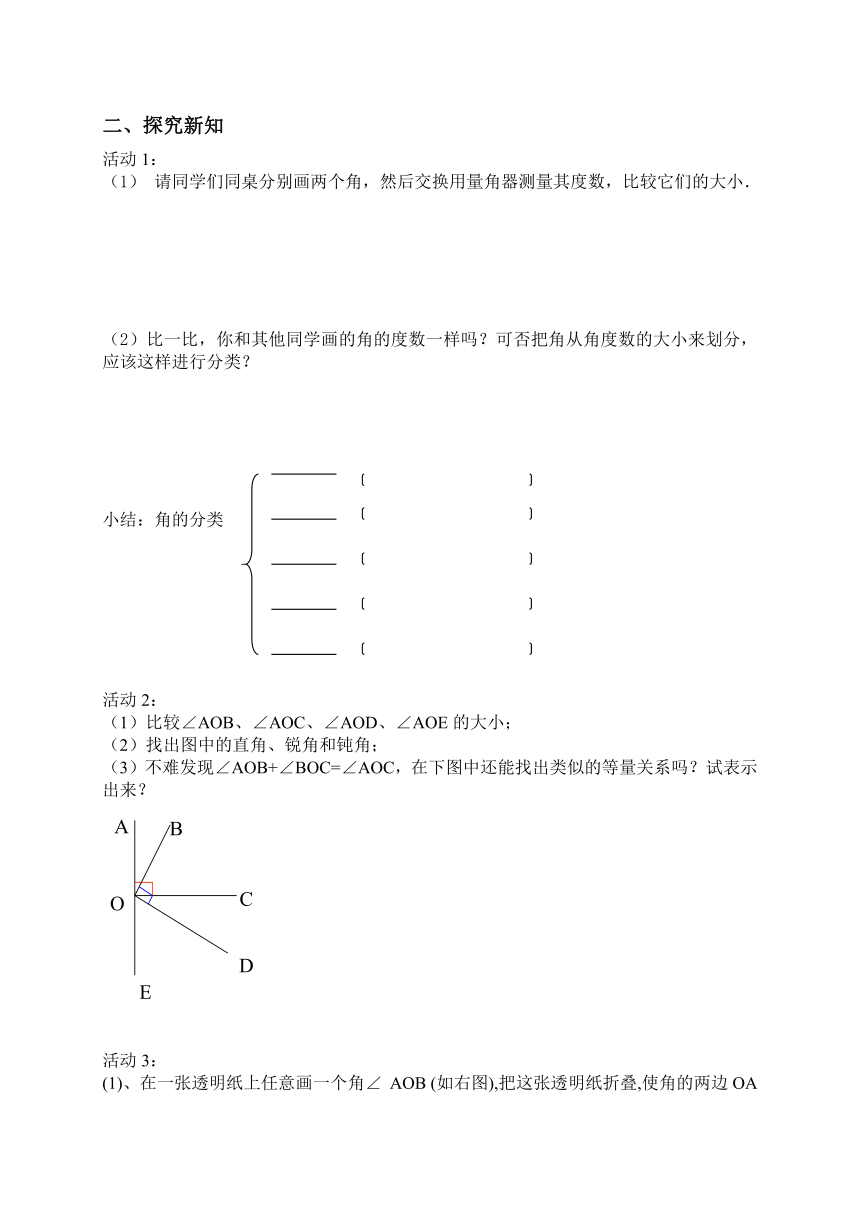
(1)比较∠AOB、∠AOC、∠AOD、∠AOE的大小;
(2)找出图中的直角、锐角和钝角;
(3)不难发现∠AOB+∠BOC=∠AOC,在下图中还能找出类似的等量关系吗?试表示出来?
活动3:
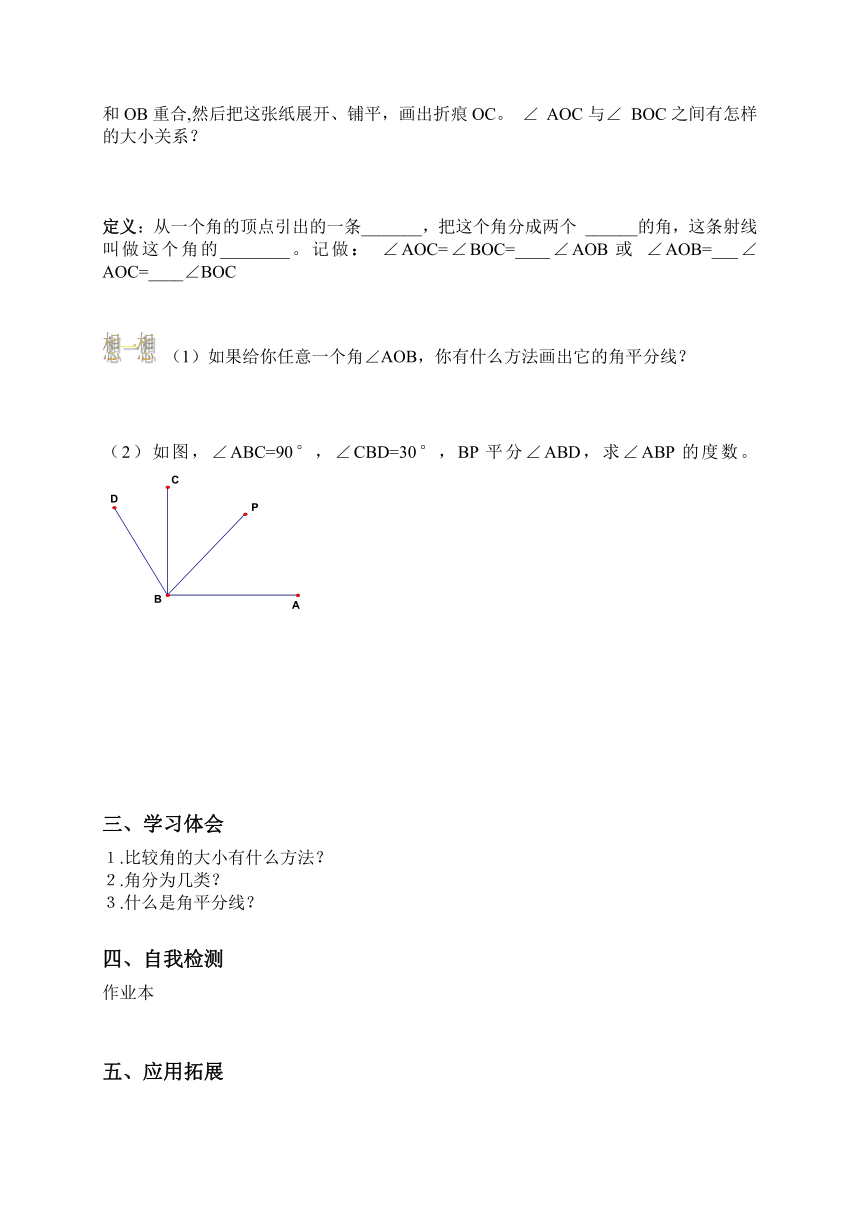
(1)、在一张透明纸上任意画一个角∠ AOB (如右图),把这张透明纸折叠,使角的两边OA和OB重合,然后把这张纸展开、铺平,画出折痕OC。 ∠ AOC与∠ BOC之间有怎样的大小关系?
定义:从一个角的顶点引出的一条_______,把这个角分成两个 ______的角,这条射线叫做这个角的________。记做: ∠AOC=∠BOC=____∠AOB或 ∠AOB=___∠AOC=____∠BOC
(1)如果给你任意一个角∠AOB,你有什么方法画出它的角平分线?
(2)如图,∠ABC=90°,∠CBD=30°,BP平分∠ABD,求∠ABP的度数。
三、学习体会
1.比较角的大小有什么方法?
2.角分为几类?
3.什么是角平分线?
四、自我检测
作业本
五、应用拓展
1、下列说法正确的是( )
A,角的边越长,则角越大。
B,角的大小与边的长短无关。
C,角的大小与顶点的位置有关。
D,角的大小决定于始边旋转的方向。
2、Ⅰ:如图若∠CBD=30 , ∠ABC=90 ,你能求出哪些角的度数?
Ⅱ:若在Ⅰ的条件下再添上BP平分∠ABD,你还能求出哪些角的度数?
3、利用一副三角板,我们能画出哪些度数的角?
学案二
学习目标:
1、了解余角和补角的概念,知道同角或等角的余角相等,同角或等角的补角相等。
2、找出互为余角和补角的角,体验余角和补角的性质的推导过程。
3、理解互为余角和互为补角主要反映了角的数量关系。
重点 余角和补角的概念和性质。
难点 有关余角和补角的性质的理解和运用。
1、 学前准备
1、 知识回顾:
上节课学习了角的分类,是根据什么来划分的?能讲出各类角的度数范围吗
2、 情境导入:
如图所示,海塘大坝的底部是石块堆积而成,量角器无法
伸入大坝底部测量,想一想,有什么办法可以测量大坝的倾斜角
3、预习疑问
二、探索、交流
1、合作学习
(1)先观察如图,∠1+∠2与Rt∠AOB相等吗?你是怎样判断的?
(2)再观察如图,∠α+∠β与∠AOB相等吗?你是怎样判断的?
(3)如果两个锐角的和是一个直角,我们就说这两个角________,简称____,也可以说其中一个角是另一个角的______。
互余的数量关系: ∠ α +∠ β =_________
如果两个角的和是一个平角,我们就说这两个角______,简称____,也可以说其中一个角是另一个角的______。
互补的数量关系: ∠ α +∠ β = _________
(4)思考:1、定义中的“互为”一词如何理解?
2、互补、互余的两角是否一定有公共顶点或公共边?
2、试一试
如图,O是直线AB上的一点,OC是 AOB的角平分线。
1.图中互余的角是______________________
2.图中互补的角是______________________
3.图中相等的角是______________________
变式:如右图,在上题的基础上添加一条射线OE,使得 DOE是一个直角,回答下列问题:
1.图中 DOC的余角有___________________
2.图中 AOD的余角有___________________
通过上述两小题你能得到什么结论?
3. AOD和 COE的补角分别是________________
通过此题,你又能得到什么结论?
3、实战演习
例1:如图、已知∠AOC= ∠BOD=Rt ∠。指出图中还有哪些角相等, 并说明理由。
例2.已知一个的补角是这个角的余角的4倍,求这个角的度数。
三、学习体会
互为余角 互为补角
对应图形
数量关系
性 质
四、自我检测
作业本
五、应用拓展
1、在一幅学校的地图上,有教学楼、食堂、图书馆三地,但被墨迹污染,图书馆的具体位置看不清,只知道图书馆在教学楼的东北方向,在食堂的南偏西60 方向,你能确定图书馆的位置吗?
A
C
E
O
B
D
B
A
C
P
D
30°
90°
1
2
A
O
B
α
β
A
O
B
A
B
O
C
D
A
B
O
C
D
E
B
A
D
C
O
4.5 角的比较与补(余)角
学案一
学习目标:
1. 会用叠合法和度量法比较两个角的大小。
2.了解角平分线的概念,并会平分一个角。
3.了解角的和差的意义,并进行角的简单计算。
教学重点:角的大小比较。
教学难点:角的和差计算。
一、学前准备
(1)、上节课我们一起研究了“角”的几何图形,什么是“角”,几何上是如何下定义的呢?
(2)、试一试,用不同的方法表示下列各角?
(3)、能比较上述角的大小吗?如果能,试阐述你的方法?
二、探究新知
活动1:
(1) 请同学们同桌分别画两个角,然后交换用量角器测量其度数,比较它们的大小.
(2)比一比,你和其他同学画的角的度数一样吗?可否把角从角度数的大小来划分,应该这样进行分类?
小结:角的分类
活动2:
(1)比较∠AOB、∠AOC、∠AOD、∠AOE的大小;
(2)找出图中的直角、锐角和钝角;
(3)不难发现∠AOB+∠BOC=∠AOC,在下图中还能找出类似的等量关系吗?试表示出来?
活动3:
(1)、在一张透明纸上任意画一个角∠ AOB (如右图),把这张透明纸折叠,使角的两边OA和OB重合,然后把这张纸展开、铺平,画出折痕OC。 ∠ AOC与∠ BOC之间有怎样的大小关系?
定义:从一个角的顶点引出的一条_______,把这个角分成两个 ______的角,这条射线叫做这个角的________。记做: ∠AOC=∠BOC=____∠AOB或 ∠AOB=___∠AOC=____∠BOC
(1)如果给你任意一个角∠AOB,你有什么方法画出它的角平分线?
(2)如图,∠ABC=90°,∠CBD=30°,BP平分∠ABD,求∠ABP的度数。
三、学习体会
1.比较角的大小有什么方法?
2.角分为几类?
3.什么是角平分线?
四、自我检测
作业本
五、应用拓展
1、下列说法正确的是( )
A,角的边越长,则角越大。
B,角的大小与边的长短无关。
C,角的大小与顶点的位置有关。
D,角的大小决定于始边旋转的方向。
2、Ⅰ:如图若∠CBD=30 , ∠ABC=90 ,你能求出哪些角的度数?
Ⅱ:若在Ⅰ的条件下再添上BP平分∠ABD,你还能求出哪些角的度数?
3、利用一副三角板,我们能画出哪些度数的角?
学案二
学习目标:
1、了解余角和补角的概念,知道同角或等角的余角相等,同角或等角的补角相等。
2、找出互为余角和补角的角,体验余角和补角的性质的推导过程。
3、理解互为余角和互为补角主要反映了角的数量关系。
重点 余角和补角的概念和性质。
难点 有关余角和补角的性质的理解和运用。
1、 学前准备
1、 知识回顾:
上节课学习了角的分类,是根据什么来划分的?能讲出各类角的度数范围吗
2、 情境导入:
如图所示,海塘大坝的底部是石块堆积而成,量角器无法
伸入大坝底部测量,想一想,有什么办法可以测量大坝的倾斜角
3、预习疑问
二、探索、交流
1、合作学习
(1)先观察如图,∠1+∠2与Rt∠AOB相等吗?你是怎样判断的?
(2)再观察如图,∠α+∠β与∠AOB相等吗?你是怎样判断的?
(3)如果两个锐角的和是一个直角,我们就说这两个角________,简称____,也可以说其中一个角是另一个角的______。
互余的数量关系: ∠ α +∠ β =_________
如果两个角的和是一个平角,我们就说这两个角______,简称____,也可以说其中一个角是另一个角的______。
互补的数量关系: ∠ α +∠ β = _________
(4)思考:1、定义中的“互为”一词如何理解?
2、互补、互余的两角是否一定有公共顶点或公共边?
2、试一试
如图,O是直线AB上的一点,OC是 AOB的角平分线。
1.图中互余的角是______________________
2.图中互补的角是______________________
3.图中相等的角是______________________
变式:如右图,在上题的基础上添加一条射线OE,使得 DOE是一个直角,回答下列问题:
1.图中 DOC的余角有___________________
2.图中 AOD的余角有___________________
通过上述两小题你能得到什么结论?
3. AOD和 COE的补角分别是________________
通过此题,你又能得到什么结论?
3、实战演习
例1:如图、已知∠AOC= ∠BOD=Rt ∠。指出图中还有哪些角相等, 并说明理由。
例2.已知一个的补角是这个角的余角的4倍,求这个角的度数。
三、学习体会
互为余角 互为补角
对应图形
数量关系
性 质
四、自我检测
作业本
五、应用拓展
1、在一幅学校的地图上,有教学楼、食堂、图书馆三地,但被墨迹污染,图书馆的具体位置看不清,只知道图书馆在教学楼的东北方向,在食堂的南偏西60 方向,你能确定图书馆的位置吗?
A
C
E
O
B
D
B
A
C
P
D
30°
90°
1
2
A
O
B
α
β
A
O
B
A
B
O
C
D
A
B
O
C
D
E
B
A
D
C
O
同课章节目录
- 第1章 有理数
- 1.1 正数和负数
- 1.2 数轴、相反数和绝对值
- 1.3 有理数的大小
- 1.4 有理数的加减
- 1.5 有理数的乘除
- 1.6 有理数的乘方
- 1.7 近似数
- 第2章 整式加减
- 2.1 代数式
- 2.2 整式加减
- 第3章 一次方程与方程组
- 3.1 一元一次方程及其解法
- 3.2 一元一次方程的应用
- 3.3二元一次方程组及其解法
- 3.4 二元一次方程组的应用
- 3.5 三元一次方程组及其解法
- 第4章 直线与角
- 4.1 几何图形
- 4.2 线段、射线、直线
- 4.3 线段的 长短比较
- 4.4 角
- 4.5 角的比较与补(余)角
- 4.6 用尺规作线段与角
- 第5章 数据的收集与整理
- 5.1 数据的 收集
- 5.2 数据的整理
- 5.3 用统计图描述数据
- 5.4 从图表中的数据获取信息
