2022-2023学年北师大版八年级数学上册1.1探索勾股定理 同步复习小测 (Word版含答案)
文档属性
| 名称 | 2022-2023学年北师大版八年级数学上册1.1探索勾股定理 同步复习小测 (Word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 184.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-19 16:25:56 | ||
图片预览

文档简介
1.1探索勾股定理---七年级同步复习小测(同步训练+课后作业)
【北师大版】
【同步训练】
一、单选题
1.如图,在 中, ,则 的中线 的长为( )
A.5 B.6 C.8 D.10
2.直角三角形纸片的两直角边长分别为6,8,现将△ABC按如图那样折叠,使点A与点B重合,折痕为DE,则DE的长为( )
A. B.5 C. D.
3.下图是一张直角三角形的纸片,两直角边AC=6cm,BC=8cm,现将△ABC折叠,使点B与点A重合,折痕为DE,则DE的长为( )
A.4cm B.5cm C. D.
4.如图,在5×5的正方形网格中,以AB为边画直角△ABC,使点C在格点上,满足这样条件的点C的个数( )
A.6 B.7 C.8 D.9
二、填空题
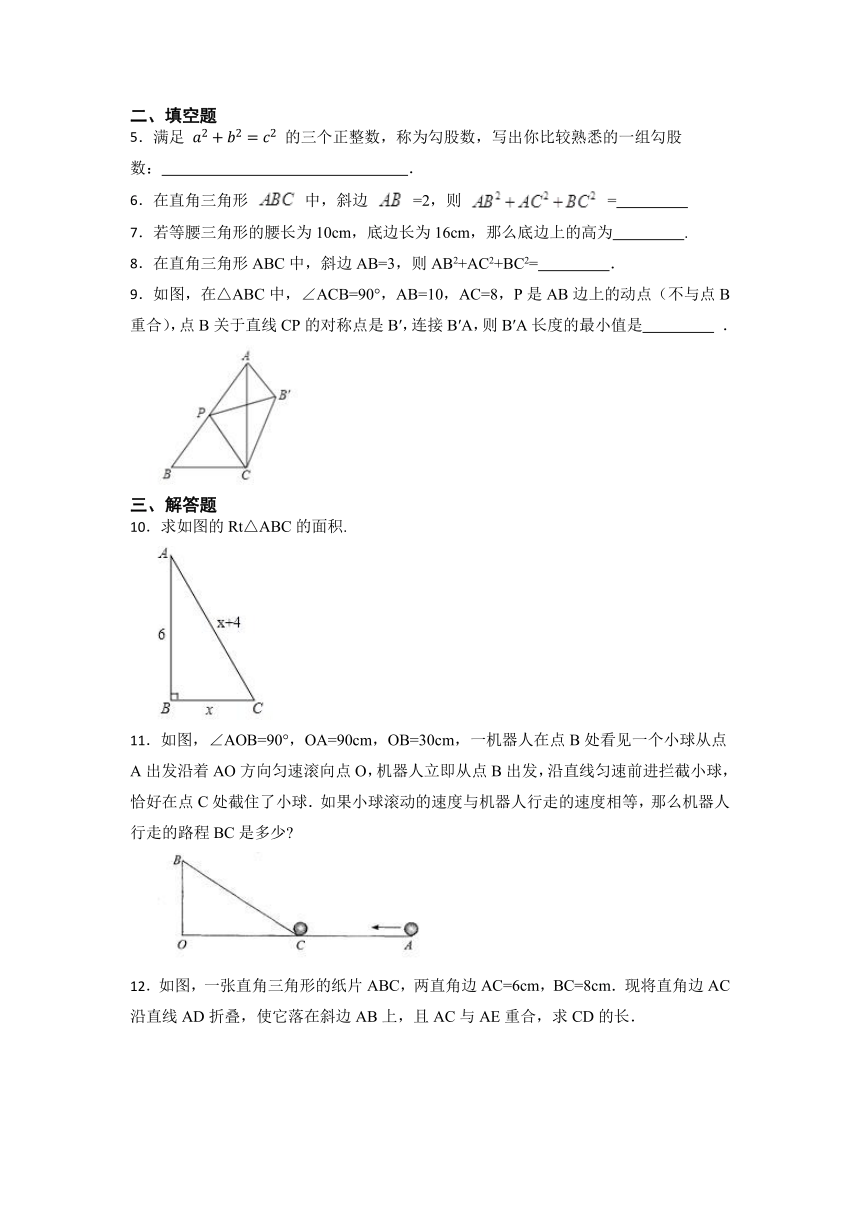
5.满足 的三个正整数,称为勾股数,写出你比较熟悉的一组勾股数: .
6.在直角三角形 中,斜边 =2,则 =
7.若等腰三角形的腰长为10cm,底边长为16cm,那么底边上的高为 .
8.在直角三角形ABC中,斜边AB=3,则AB2+AC2+BC2= .
9.如图,在△ABC中,∠ACB=90°,AB=10,AC=8,P是AB边上的动点(不与点B重合),点B关于直线CP的对称点是B′,连接B′A,则B′A长度的最小值是 .
三、解答题
10.求如图的Rt△ABC的面积.
11.如图,∠AOB=90°,OA=90cm,OB=30cm,一机器人在点B处看见一个小球从点A出发沿着AO方向匀速滚向点O,机器人立即从点B出发,沿直线匀速前进拦截小球,恰好在点C处截住了小球.如果小球滚动的速度与机器人行走的速度相等,那么机器人行走的路程BC是多少
12.如图,一张直角三角形的纸片ABC,两直角边AC=6cm,BC=8cm.现将直角边AC沿直线AD折叠,使它落在斜边AB上,且AC与AE重合,求CD的长.
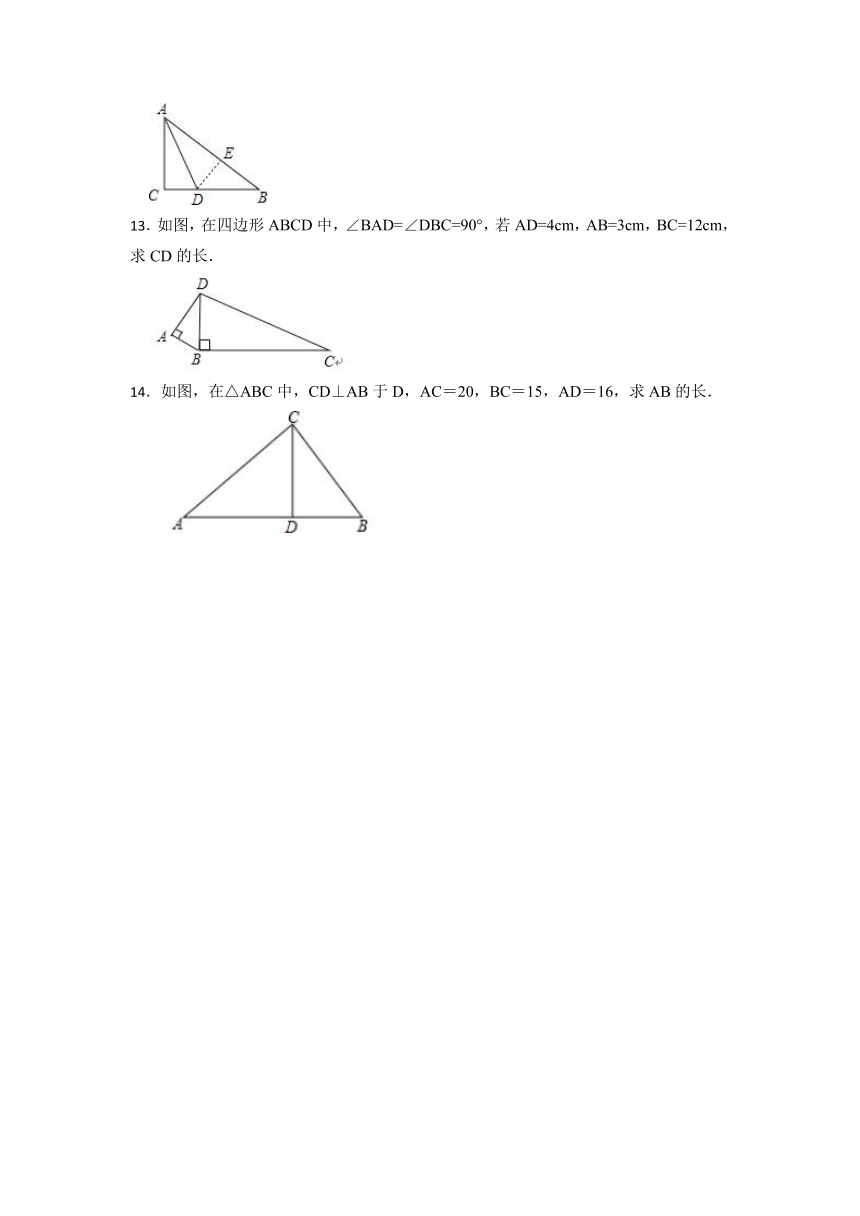
13.如图,在四边形ABCD中,∠BAD=∠DBC=90°,若AD=4cm,AB=3cm,BC=12cm,求CD的长.
14.如图,在△ABC中,CD⊥AB于D,AC=20,BC=15,AD=16,求AB的长.
【课后作业】
一、单选题
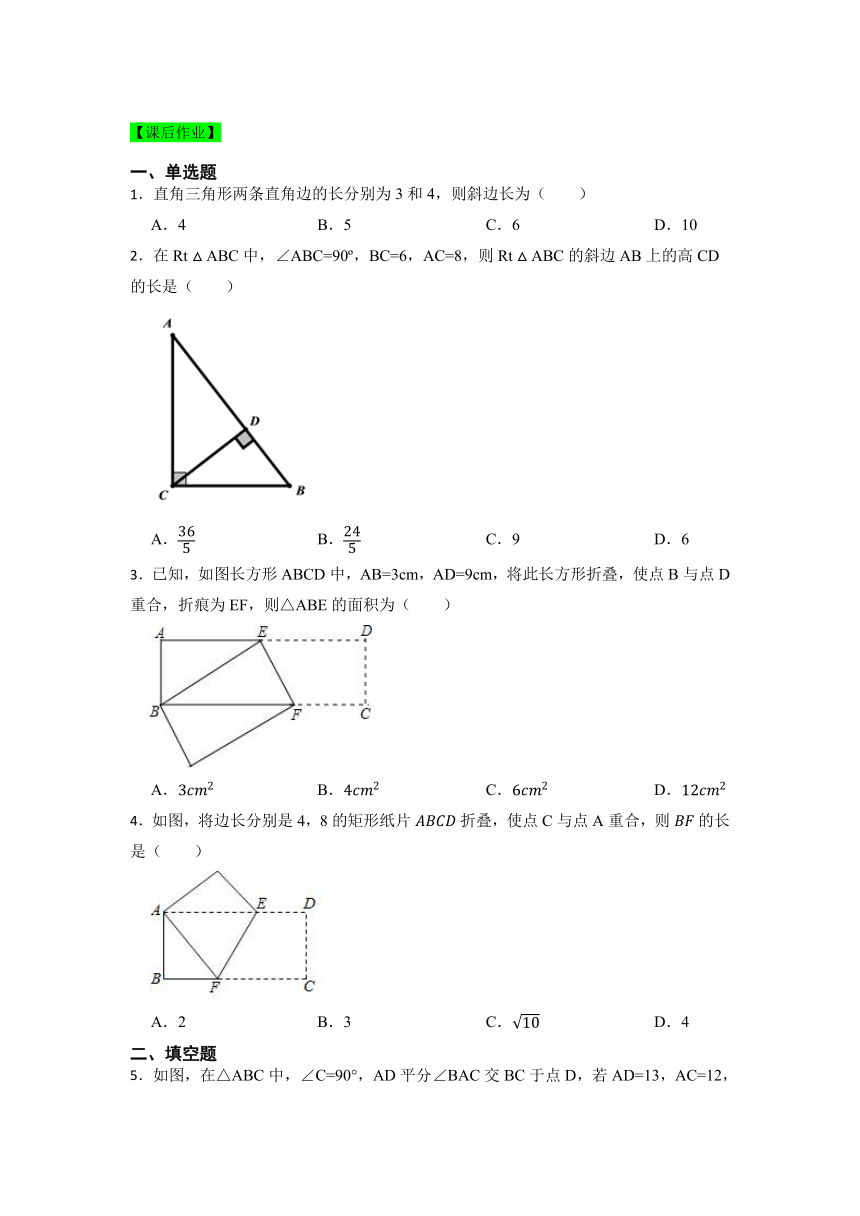
1.直角三角形两条直角边的长分别为3和4,则斜边长为( )
A.4 B.5 C.6 D.10
2.在Rt ABC中,∠ABC=90 ,BC=6,AC=8,则Rt ABC的斜边AB上的高CD的长是( )
A. B. C.9 D.6
3.已知,如图长方形ABCD中,AB=3cm,AD=9cm,将此长方形折叠,使点B与点D重合,折痕为EF,则△ABE的面积为( )
A. B. C. D.
4.如图,将边长分别是4,8的矩形纸片折叠,使点C与点A重合,则的长是( )
A.2 B.3 C. D.4
二、填空题
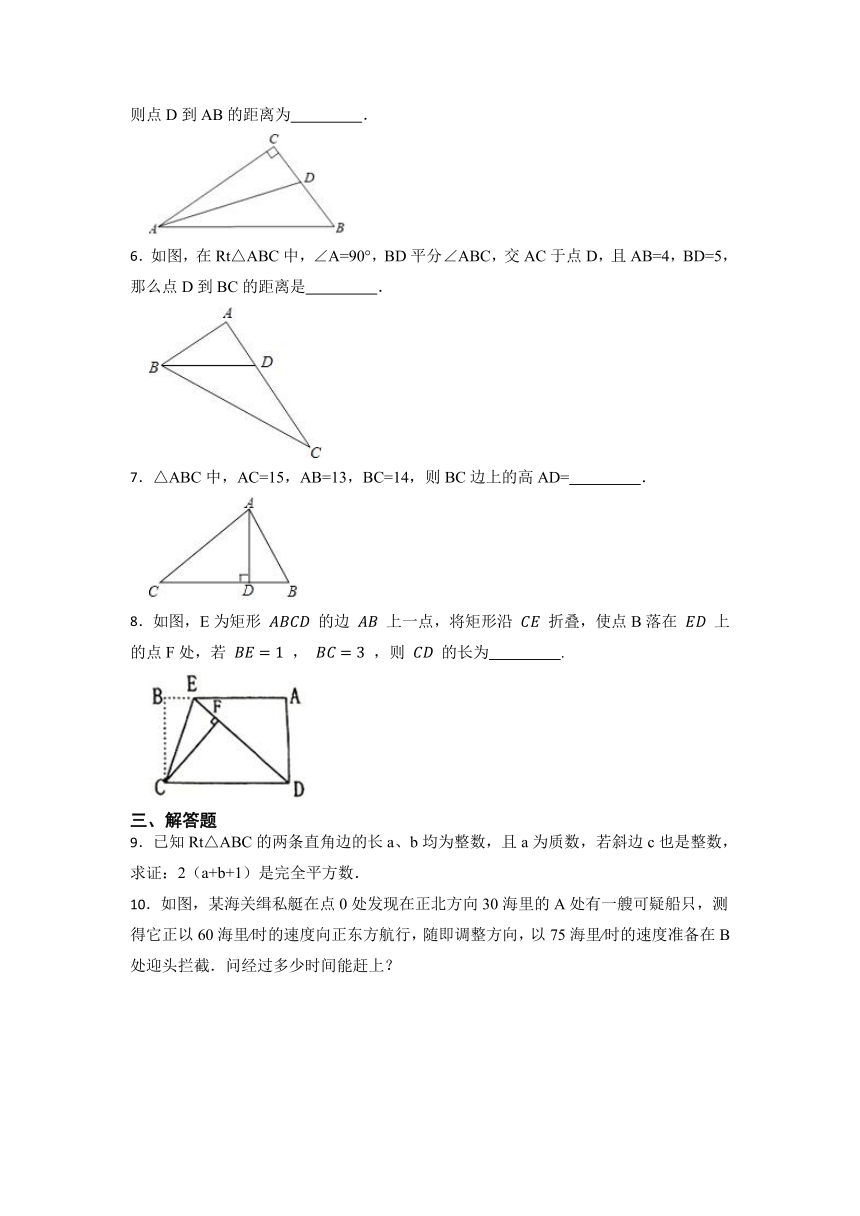
5.如图,在△ABC中,∠C=90°,AD平分∠BAC交BC于点D,若AD=13,AC=12,则点D到AB的距离为 .
6.如图,在Rt△ABC中,∠A=90°,BD平分∠ABC,交AC于点D,且AB=4,BD=5,那么点D到BC的距离是 .
7.△ABC中,AC=15,AB=13,BC=14,则BC边上的高AD= .
8.如图,E为矩形 的边 上一点,将矩形沿 折叠,使点B落在 上的点F处,若 , ,则 的长为 .
三、解答题
9.已知Rt△ABC的两条直角边的长a、b均为整数,且a为质数,若斜边c也是整数,求证:2(a+b+1)是完全平方数.
10.如图,某海关缉私艇在点0处发现在正北方向30海里的A处有一艘可疑船只,测得它正以60海里∕时的速度向正东方航行,随即调整方向,以75海里∕时的速度准备在B处迎头拦截.问经过多少时间能赶上?
11.把一张矩形ABCD纸片按如图方式折叠,使点A与点E重合,点C与点F重合(E、F两点均在BD上),折痕分别为BH、DG.
(1)求证:△BHE≌△DGF;
(2)若AB=6cm,BC=8cm,求线段FG的长.
12.已知在 中, , , 是 上一点,且 ,求 的长.
13.如图,在 中, , , ,将 折叠,使点 恰好落在斜边 上,与点 重合, 为折痕,求 和 的长.
答案解析部分
1.【答案】A
【解析】【解答】解:Rt△ABC中,∠ACB=90°,AC=6,BC=8,
∴AB= =10,
∵CD是Rt△ABC的中线,
∴CD= AB=5,
故答案为:A.
【分析】首先根据勾股定理算出AB的长,再根据直角三角形斜边上的中线等于斜边的一半即可由CD= AB得出答案.
2.【答案】A
【解析】【解答】∵∠C=90°,AC=8,BC=6,∴AB 10.
∵折叠,∴BE=AE,AD=BD=5,DE⊥AB.
在Rt△BEC中,BE2=BC2+CE2,∴BE2=36+(8﹣BE)2,∴BE .
在Rt△BDE中,DE .
故选A.
【分析】根据勾股定理可求AB=10,由折叠的性质可得BE=AE,AD=BD=5,DE⊥AB,根据勾股定理可求BE的长,DE的长.
3.【答案】C
【解析】【解答】解:在Rt△ABC中,AB=
由折叠可知:BD=AD,AE=AB=5
∴CD=8-AD
在Rt△ADC中,AC2+CD2=AD2,即62+(8-AD)2=AD2
解得 AD=
同理可得 DE=.
故答案为:C
【分析】设AD为x.先在Rt△ABC中,利用勾股定理求出AB,然后由轴对称的性质可得BD=AD,AE=AB=5,进而得CD=8-AD;进而在Rt△ADC中利用勾股定理列方程求出AD,最后在Rt△ADE中利用勾股定理即可求出DE。
4.【答案】C
【解析】【解答】解:根据题意可得以AB为边画直角△ABC,使点C在格点上,满足这样条件的点C共 8个.
故选C.
【分析】如图,在5×5的正方形网格中,以AB为边画直角△ABC,使点C在格点上,满足这样条件的点C的个数.
5.【答案】 , , (答案不唯一)
【解析】【解答】∵ 符合 .
∴我较熟悉的一组勾股数是: , , (答案不唯一).
【分析】根据勾股定理和正整数,可以得出许多组勾股数,如:(1)当a为奇数时,其平方可拆成两个连续自然数的和(此两个数便是b、c),若a=3时,32=9=4+5,即:3 2 + 4 2 = 5 2,若a=5时,52=25=12+13,即:52+122=132......以此类推;(2)当a为偶数时,其一半的平方加1和减1便是b、c,若a=6时,a的一半为3,32-1=8,32+1=10,即:62+82=102,若a=8时,a的一半为4,42-1=15,42+1=17,即:82+152=172,.......以此类推。
6.【答案】8
【解析】【解答】由题意AB =4,AC +BC =AB ,所以AB +AC +BC =8
【分析】直接用勾股定理可求解。
7.【答案】6cm
【解析】【解答】作AD⊥BC于D,
∵AB=AC=16cm,
∴BD=BC=8cm,
∴AD= ,
故答案为:6cm.
【分析】作AD⊥BC于D,利用等腰三角形三线合一的性质,可求出BD的长,再利用勾股定理求出AD。
8.【答案】18
【解析】【解答】解:∵直角三角形ABC中,斜边AB=3,
∴AC2+BC2=AB2=32=9,
∴AB2+AC2+BC2=2AB2=2×9=18;
故答案为:18.
【分析】由勾股定理求出AC2+BC2=AB2,即可得出结果.
9.【答案】2
【解析】【解答】解:在Rt△ABC中,由勾股定理可知:BC===6,
由轴对称的性质可知:BC=CB′=6,
∵CB′长度固定不变,
∴当AB′+CB′有最小值时,AB′的长度有最小值.
根据两点之间线段最短可知:A、B′、C三点在一条直线上时,AB′有最小值,
∴AB′=AC﹣B′C=8﹣6=2.
故答案为:2.
【分析】首先由勾股定理求得BC的长度,由轴对称的性质可知BC=CB′=6,当B′A有最小值时,即AB′+CB′有最小值,由两点之间线段最短可知当A、B′、C三点在一条直线上时,AB′有最小值.
10.【答案】解:由勾股定理得:(x+4)2=36+x2,
解得:x= ,
所以△ABC的面积= ×6× =7.5.
故答案为7.5.
【解析】【分析】首先利用勾股定理得到三边关系,进而建立关于x的方程,解方程求出x的值,再利用三角形的面积公式计算即可.
11.【答案】解:∵小球滚动的速度与机器人行走的速度相等 ∴BC=AC
设BC=AC=xcm ∴OC=(90-x)cm 在Rt△BOC中,
∴ 解得:x=50
答:机器人行走的路程BC为50cm
【解析】【分析】根据小球滚动的速度与机器人行走的速度相等 知BC=AC,设BC=AC=xcm ∴OC=(90-x)cm 在Rt△BOC中利用勾股定理列出方程求解即可。
12.【答案】解:∵△ABC是直角三角形,AC=6cm,BC=8cm,∴AB= = =10cm,∵△AED是△ACD翻折而成,∴AE=AC=6cm,设DE=CD=xcm,∠AED=90°,∴BE=AB﹣AE=10﹣6=4(cm),在Rt△BDE中,BD2=DE2+BE2,即(8﹣x)2=42+x2,解得x=3.故CD的长为3cm.
【解析】【分析】先由勾股定理求出AB的长,由题意知AE=AC=6cm,则BE=4,设DE=CD=xcm,在Rt△BDE中,由勾股定理求出x值即可答案.
13.【答案】解:∵∠BAD=∠DBC=90°,
∴△ADB、△BDC均是直角三角形,
由题意得,AD=4cm,AB=3cm,BC=12cm,
在Rt△ABD中,BD==5cm,
在Rt△BDC中,DC= =13cm.
【解析】【分析】先根据勾股定理求出BD的长,再根据勾股定理求得CD的长即可.
14.【答案】解:∵CD⊥AB于D,
∴∠ADC=∠BDC=90°.
∵在直角△ACD中,AC=20,AD=16,
∴CD= =12;
∵在直角△BCD中,BC=15,CD=12,
∴BD= =9,
∴AB=AD+BD=25.
【解析】【分析】在直角△ACD中利用勾股定理得出CD的长,再利用在直角△BCD中利用勾股定理求得BD,再根据线段的和差关系求得AB的长.
答案解析部分
1.【答案】B
【解析】【解答】由勾股定理得:斜边长为: =5.
故答案为:B.
【分析】根据已知条件直角三角形两条直角边的长分别为3和4,再利用勾股定理求斜边的长度即可作答。
2.【答案】B
【解析】【解答】解:由勾股定理有: ,
在Rt△ABC中,由等面积法可知: ,
代入数据: ,
解得: ,
故答案为:B.
【分析】先由勾股定理算出AB=10,然后再由Rt△ABC中等面积法得到 即可求解.
3.【答案】C
【解析】【解答】由折叠的性质可得DE=BE,
设AE=xcm ,则BE=DE=(9-x)cm,
在Rt 中,由勾股定理得:32+ x2=(9-x)2
解得:x=4,
∴AE=4cm,
∴S△ABE= ×4×3=6(cm2),
故答案为:C.
【分析】由折叠的性质可得DE=BE,设AE=xcm ,则BE=DE=(9-x)cm,利用勾股定理得出AE的值,再利用三角形面积公式计算即可。
4.【答案】B
【解析】【解答】解:由折叠的性质可知:AF=CF.
设BF=m,则AF=CF=8 m,
在Rt△ABF中,∠ABF=90°,AB=4,BF=m,AF=8 m,
∴ ,即 ,
∴m=3.
故答案为:B.
【分析】由折叠的性质可知AF=CF,设BF=m,则AF=CF=8 m,在Rt△ABF中,由勾股定理可建立关于m方程,并解之即可.
5.【答案】5
【解析】【解答】作DE⊥AB交AB于点E,
∵AD平分∠BAC,
∴CD=DE,
∵AD=13,AC=12,
∴CD= =5,
∴DE=5.
故答案为:5.
【分析】根据勾股定理可得CD长,由角平分线上的点到角两边的距离相等即可知点D到AB的距离与CD相等.
6.【答案】3
【解析】【解答】解:过点D作DE⊥BC于E,
∵在Rt△ABC中,∠A=90°,BD平分∠ABC,
即AD⊥BA,
∴DE=AD,
∵在Rt△ABD中,∠A=90°,AB=4,BD=5,
∴AD= =3,
∴DE=AD=3,
∴点D到BC的距离是3.
故答案为:3.
【分析】过点D作DE⊥BC于E, 根据角平分线的性质定理得出DE=AD,在Rt△ABD中由勾股定理得出AD的长即可。
7.【答案】12
【解析】【解答】解:设BD=x,则CD=14﹣x,
在Rt△ABD中,AD2+x2=132,
在Rt△ADC中,AD2=152﹣(14﹣x)2,
则有132﹣x2=152﹣(14﹣x)2,
132﹣x2=152﹣196+28x﹣x2,
解得x=5,
在Rt△ABD中,AD= =12.
故答案为:12.
【分析】AD为高,那么题中有两个直角三角形.AD在这两个直角三角形中,设BD为未知数,可利用勾股定理都表示出AD长.求得BD长,再根据勾股定理求得AD长.
8.【答案】5
【解析】【解答】解:由题意可知AD=BC=CF, ∠AED=∠CDF, ∠A=∠CFD=90°,
所以△AED≌△FDC,
所以ED=CD,
设AE=x,则x +3 =(x+1) ,
解得x=4,
所以CD=5.
故答案是:5.
【分析】利用矩形的性质及折叠的性质,可证得AD=BC=CF, ∠AED=∠CDF, ∠A=∠CFD=90°及△AED≌△FDC,利用全等三角形的对应边相等,可得到ED=CD,设AE=x,利用勾股定理,建立关于x的方程,解方程求出x的值,即可得到CD的长。
9.【答案】解:∵a,b是Rt△ABC的两条直角边,c是斜边,∴a2+b2=c2,即a2=c2﹣b2=(c+b)(c﹣b),∵a为质数,∴c+b=a2,c﹣b=1,∴a2=2b+1,∴2(a+b+1)=a2+2a+1=(a+1)2,∴2(a+b+1)是完全平方数.
【解析】【分析】由勾股定理变形得a2=c2﹣b2=(c+b)(c﹣b),根据a为质数可得c+b=a2,c﹣b=1,于是可得a2=2b+1,代入2(a+b+1)可得证。
10.【答案】解:设经过x小时能赶上,则OB=75x,则AB=60x.在直角△ABC中,∵OB2=OA2+AB2,∴(75x)2=302+(60x)2,解得:x= ,故经过时间为 小时. 答:经过 小时能赶上.
【解析】【分析】 设经过x小时能赶上,则OB=75x,则AB=60x.在直角△ABC中 ,利用勾股定理建立方程,求解即可得出答案。
11.【答案】(1)证明:∵四边形ABCD是矩形,
∴AB=CD,∠A=∠C=90°,∠ABD=∠BDC,
∵△BEH是△BAH翻折而成,
∴∠ABH=∠EBH,∠A=∠HEB=90°,AB=BE,
∵△DGF是△DGC翻折而成,
∴∠FDG=∠CDG,∠C=∠DFG=90°,CD=DF,
∴∠DBH=∠ABD,∠BDG=∠BDC,
∴∠DBH=∠BDG,
∴△BEH与△DFG中,
∠HEB=∠DFG,BE=DF,∠DBH=∠BDG,
∴△BEH≌△DFG,
(2)解:∵四边形ABCD是矩形,AB=6cm,BC=8cm,
∴AB=CD=6cm,AD=BC=8cm,
∴BD===10,
∵由(1)知,FD=CD,CG=FG,
∴BF=10-6=4cm,
设FG=x,则BG=8-x,
在Rt△BGF中,
BG2=BF2+FG2,即(8-x)2=42+x2,
解得x=3,即FG=3cm.
【解析】【分析】(1)先根据矩形的性质得出∠ABD=∠BDC,再由图形折叠的性质得出∠ABH=∠EBH,∠FDG=∠CDG,∠A=∠HEB=90°,∠C=∠DFG=90°,进而可得出△BEH≌△DFG;
(2)先根据勾股定理得出BD的长,进而得出BF的长,由图形翻折变换的性质得出CG=FG,设FG=x,则BG=8-x,再利用勾股定理即可求出x的值.
12.【答案】解:如图,过点A作AE⊥BC于点E,
∵AB=AC=20,BC=32,
∴BE=CE=16,
在Rt△ACE中,利用勾股定理可知:AE= ,
设BD=x,则DE=16﹣x,DC=32﹣x,
又DA⊥CA,
在Rt△ADE和Rt△ADC中分别利用勾股定理得: ,
代入为: ,
整理得:
解得: .
即BD=7.
【解析】【分析】过点A作AE⊥BC于点E,首先根据等腰三角形的三线合一得出 BE=CE=16, 在Rt△ACE中,用勾股定理可求得AE的值,设BD=x,则DE=16﹣x,DC=32﹣x,在Rt△ADE和Rt△ADC中分别利用勾股定理可将AD2用含x的代数式表示并列出关于x的方程,解方程即可求解.
13.【答案】解:设EB′=x,
∵∠B=90°,AB=6,BC=8,
∴AC= ,
由折叠的性质可知,BE=EB′=x,AB′=AB=6,
则CB′=AC-AB′=4,EC=BC-BE=8-x,
由勾股定理得,x2+42=(8-x)2,
解得x=3,
∴EB′=3.
【解析】【分析】先利用勾股定理求出AC=10,再求出 x2+42=(8-x)2, 最后计算求解即可。
【北师大版】
【同步训练】
一、单选题
1.如图,在 中, ,则 的中线 的长为( )
A.5 B.6 C.8 D.10
2.直角三角形纸片的两直角边长分别为6,8,现将△ABC按如图那样折叠,使点A与点B重合,折痕为DE,则DE的长为( )
A. B.5 C. D.
3.下图是一张直角三角形的纸片,两直角边AC=6cm,BC=8cm,现将△ABC折叠,使点B与点A重合,折痕为DE,则DE的长为( )
A.4cm B.5cm C. D.
4.如图,在5×5的正方形网格中,以AB为边画直角△ABC,使点C在格点上,满足这样条件的点C的个数( )
A.6 B.7 C.8 D.9
二、填空题
5.满足 的三个正整数,称为勾股数,写出你比较熟悉的一组勾股数: .
6.在直角三角形 中,斜边 =2,则 =
7.若等腰三角形的腰长为10cm,底边长为16cm,那么底边上的高为 .
8.在直角三角形ABC中,斜边AB=3,则AB2+AC2+BC2= .
9.如图,在△ABC中,∠ACB=90°,AB=10,AC=8,P是AB边上的动点(不与点B重合),点B关于直线CP的对称点是B′,连接B′A,则B′A长度的最小值是 .
三、解答题
10.求如图的Rt△ABC的面积.
11.如图,∠AOB=90°,OA=90cm,OB=30cm,一机器人在点B处看见一个小球从点A出发沿着AO方向匀速滚向点O,机器人立即从点B出发,沿直线匀速前进拦截小球,恰好在点C处截住了小球.如果小球滚动的速度与机器人行走的速度相等,那么机器人行走的路程BC是多少
12.如图,一张直角三角形的纸片ABC,两直角边AC=6cm,BC=8cm.现将直角边AC沿直线AD折叠,使它落在斜边AB上,且AC与AE重合,求CD的长.
13.如图,在四边形ABCD中,∠BAD=∠DBC=90°,若AD=4cm,AB=3cm,BC=12cm,求CD的长.
14.如图,在△ABC中,CD⊥AB于D,AC=20,BC=15,AD=16,求AB的长.
【课后作业】
一、单选题
1.直角三角形两条直角边的长分别为3和4,则斜边长为( )
A.4 B.5 C.6 D.10
2.在Rt ABC中,∠ABC=90 ,BC=6,AC=8,则Rt ABC的斜边AB上的高CD的长是( )
A. B. C.9 D.6
3.已知,如图长方形ABCD中,AB=3cm,AD=9cm,将此长方形折叠,使点B与点D重合,折痕为EF,则△ABE的面积为( )
A. B. C. D.
4.如图,将边长分别是4,8的矩形纸片折叠,使点C与点A重合,则的长是( )
A.2 B.3 C. D.4
二、填空题
5.如图,在△ABC中,∠C=90°,AD平分∠BAC交BC于点D,若AD=13,AC=12,则点D到AB的距离为 .
6.如图,在Rt△ABC中,∠A=90°,BD平分∠ABC,交AC于点D,且AB=4,BD=5,那么点D到BC的距离是 .
7.△ABC中,AC=15,AB=13,BC=14,则BC边上的高AD= .
8.如图,E为矩形 的边 上一点,将矩形沿 折叠,使点B落在 上的点F处,若 , ,则 的长为 .
三、解答题
9.已知Rt△ABC的两条直角边的长a、b均为整数,且a为质数,若斜边c也是整数,求证:2(a+b+1)是完全平方数.
10.如图,某海关缉私艇在点0处发现在正北方向30海里的A处有一艘可疑船只,测得它正以60海里∕时的速度向正东方航行,随即调整方向,以75海里∕时的速度准备在B处迎头拦截.问经过多少时间能赶上?
11.把一张矩形ABCD纸片按如图方式折叠,使点A与点E重合,点C与点F重合(E、F两点均在BD上),折痕分别为BH、DG.
(1)求证:△BHE≌△DGF;
(2)若AB=6cm,BC=8cm,求线段FG的长.
12.已知在 中, , , 是 上一点,且 ,求 的长.
13.如图,在 中, , , ,将 折叠,使点 恰好落在斜边 上,与点 重合, 为折痕,求 和 的长.
答案解析部分
1.【答案】A
【解析】【解答】解:Rt△ABC中,∠ACB=90°,AC=6,BC=8,
∴AB= =10,
∵CD是Rt△ABC的中线,
∴CD= AB=5,
故答案为:A.
【分析】首先根据勾股定理算出AB的长,再根据直角三角形斜边上的中线等于斜边的一半即可由CD= AB得出答案.
2.【答案】A
【解析】【解答】∵∠C=90°,AC=8,BC=6,∴AB 10.
∵折叠,∴BE=AE,AD=BD=5,DE⊥AB.
在Rt△BEC中,BE2=BC2+CE2,∴BE2=36+(8﹣BE)2,∴BE .
在Rt△BDE中,DE .
故选A.
【分析】根据勾股定理可求AB=10,由折叠的性质可得BE=AE,AD=BD=5,DE⊥AB,根据勾股定理可求BE的长,DE的长.
3.【答案】C
【解析】【解答】解:在Rt△ABC中,AB=
由折叠可知:BD=AD,AE=AB=5
∴CD=8-AD
在Rt△ADC中,AC2+CD2=AD2,即62+(8-AD)2=AD2
解得 AD=
同理可得 DE=.
故答案为:C
【分析】设AD为x.先在Rt△ABC中,利用勾股定理求出AB,然后由轴对称的性质可得BD=AD,AE=AB=5,进而得CD=8-AD;进而在Rt△ADC中利用勾股定理列方程求出AD,最后在Rt△ADE中利用勾股定理即可求出DE。
4.【答案】C
【解析】【解答】解:根据题意可得以AB为边画直角△ABC,使点C在格点上,满足这样条件的点C共 8个.
故选C.
【分析】如图,在5×5的正方形网格中,以AB为边画直角△ABC,使点C在格点上,满足这样条件的点C的个数.
5.【答案】 , , (答案不唯一)
【解析】【解答】∵ 符合 .
∴我较熟悉的一组勾股数是: , , (答案不唯一).
【分析】根据勾股定理和正整数,可以得出许多组勾股数,如:(1)当a为奇数时,其平方可拆成两个连续自然数的和(此两个数便是b、c),若a=3时,32=9=4+5,即:3 2 + 4 2 = 5 2,若a=5时,52=25=12+13,即:52+122=132......以此类推;(2)当a为偶数时,其一半的平方加1和减1便是b、c,若a=6时,a的一半为3,32-1=8,32+1=10,即:62+82=102,若a=8时,a的一半为4,42-1=15,42+1=17,即:82+152=172,.......以此类推。
6.【答案】8
【解析】【解答】由题意AB =4,AC +BC =AB ,所以AB +AC +BC =8
【分析】直接用勾股定理可求解。
7.【答案】6cm
【解析】【解答】作AD⊥BC于D,
∵AB=AC=16cm,
∴BD=BC=8cm,
∴AD= ,
故答案为:6cm.
【分析】作AD⊥BC于D,利用等腰三角形三线合一的性质,可求出BD的长,再利用勾股定理求出AD。
8.【答案】18
【解析】【解答】解:∵直角三角形ABC中,斜边AB=3,
∴AC2+BC2=AB2=32=9,
∴AB2+AC2+BC2=2AB2=2×9=18;
故答案为:18.
【分析】由勾股定理求出AC2+BC2=AB2,即可得出结果.
9.【答案】2
【解析】【解答】解:在Rt△ABC中,由勾股定理可知:BC===6,
由轴对称的性质可知:BC=CB′=6,
∵CB′长度固定不变,
∴当AB′+CB′有最小值时,AB′的长度有最小值.
根据两点之间线段最短可知:A、B′、C三点在一条直线上时,AB′有最小值,
∴AB′=AC﹣B′C=8﹣6=2.
故答案为:2.
【分析】首先由勾股定理求得BC的长度,由轴对称的性质可知BC=CB′=6,当B′A有最小值时,即AB′+CB′有最小值,由两点之间线段最短可知当A、B′、C三点在一条直线上时,AB′有最小值.
10.【答案】解:由勾股定理得:(x+4)2=36+x2,
解得:x= ,
所以△ABC的面积= ×6× =7.5.
故答案为7.5.
【解析】【分析】首先利用勾股定理得到三边关系,进而建立关于x的方程,解方程求出x的值,再利用三角形的面积公式计算即可.
11.【答案】解:∵小球滚动的速度与机器人行走的速度相等 ∴BC=AC
设BC=AC=xcm ∴OC=(90-x)cm 在Rt△BOC中,
∴ 解得:x=50
答:机器人行走的路程BC为50cm
【解析】【分析】根据小球滚动的速度与机器人行走的速度相等 知BC=AC,设BC=AC=xcm ∴OC=(90-x)cm 在Rt△BOC中利用勾股定理列出方程求解即可。
12.【答案】解:∵△ABC是直角三角形,AC=6cm,BC=8cm,∴AB= = =10cm,∵△AED是△ACD翻折而成,∴AE=AC=6cm,设DE=CD=xcm,∠AED=90°,∴BE=AB﹣AE=10﹣6=4(cm),在Rt△BDE中,BD2=DE2+BE2,即(8﹣x)2=42+x2,解得x=3.故CD的长为3cm.
【解析】【分析】先由勾股定理求出AB的长,由题意知AE=AC=6cm,则BE=4,设DE=CD=xcm,在Rt△BDE中,由勾股定理求出x值即可答案.
13.【答案】解:∵∠BAD=∠DBC=90°,
∴△ADB、△BDC均是直角三角形,
由题意得,AD=4cm,AB=3cm,BC=12cm,
在Rt△ABD中,BD==5cm,
在Rt△BDC中,DC= =13cm.
【解析】【分析】先根据勾股定理求出BD的长,再根据勾股定理求得CD的长即可.
14.【答案】解:∵CD⊥AB于D,
∴∠ADC=∠BDC=90°.
∵在直角△ACD中,AC=20,AD=16,
∴CD= =12;
∵在直角△BCD中,BC=15,CD=12,
∴BD= =9,
∴AB=AD+BD=25.
【解析】【分析】在直角△ACD中利用勾股定理得出CD的长,再利用在直角△BCD中利用勾股定理求得BD,再根据线段的和差关系求得AB的长.
答案解析部分
1.【答案】B
【解析】【解答】由勾股定理得:斜边长为: =5.
故答案为:B.
【分析】根据已知条件直角三角形两条直角边的长分别为3和4,再利用勾股定理求斜边的长度即可作答。
2.【答案】B
【解析】【解答】解:由勾股定理有: ,
在Rt△ABC中,由等面积法可知: ,
代入数据: ,
解得: ,
故答案为:B.
【分析】先由勾股定理算出AB=10,然后再由Rt△ABC中等面积法得到 即可求解.
3.【答案】C
【解析】【解答】由折叠的性质可得DE=BE,
设AE=xcm ,则BE=DE=(9-x)cm,
在Rt 中,由勾股定理得:32+ x2=(9-x)2
解得:x=4,
∴AE=4cm,
∴S△ABE= ×4×3=6(cm2),
故答案为:C.
【分析】由折叠的性质可得DE=BE,设AE=xcm ,则BE=DE=(9-x)cm,利用勾股定理得出AE的值,再利用三角形面积公式计算即可。
4.【答案】B
【解析】【解答】解:由折叠的性质可知:AF=CF.
设BF=m,则AF=CF=8 m,
在Rt△ABF中,∠ABF=90°,AB=4,BF=m,AF=8 m,
∴ ,即 ,
∴m=3.
故答案为:B.
【分析】由折叠的性质可知AF=CF,设BF=m,则AF=CF=8 m,在Rt△ABF中,由勾股定理可建立关于m方程,并解之即可.
5.【答案】5
【解析】【解答】作DE⊥AB交AB于点E,
∵AD平分∠BAC,
∴CD=DE,
∵AD=13,AC=12,
∴CD= =5,
∴DE=5.
故答案为:5.
【分析】根据勾股定理可得CD长,由角平分线上的点到角两边的距离相等即可知点D到AB的距离与CD相等.
6.【答案】3
【解析】【解答】解:过点D作DE⊥BC于E,
∵在Rt△ABC中,∠A=90°,BD平分∠ABC,
即AD⊥BA,
∴DE=AD,
∵在Rt△ABD中,∠A=90°,AB=4,BD=5,
∴AD= =3,
∴DE=AD=3,
∴点D到BC的距离是3.
故答案为:3.
【分析】过点D作DE⊥BC于E, 根据角平分线的性质定理得出DE=AD,在Rt△ABD中由勾股定理得出AD的长即可。
7.【答案】12
【解析】【解答】解:设BD=x,则CD=14﹣x,
在Rt△ABD中,AD2+x2=132,
在Rt△ADC中,AD2=152﹣(14﹣x)2,
则有132﹣x2=152﹣(14﹣x)2,
132﹣x2=152﹣196+28x﹣x2,
解得x=5,
在Rt△ABD中,AD= =12.
故答案为:12.
【分析】AD为高,那么题中有两个直角三角形.AD在这两个直角三角形中,设BD为未知数,可利用勾股定理都表示出AD长.求得BD长,再根据勾股定理求得AD长.
8.【答案】5
【解析】【解答】解:由题意可知AD=BC=CF, ∠AED=∠CDF, ∠A=∠CFD=90°,
所以△AED≌△FDC,
所以ED=CD,
设AE=x,则x +3 =(x+1) ,
解得x=4,
所以CD=5.
故答案是:5.
【分析】利用矩形的性质及折叠的性质,可证得AD=BC=CF, ∠AED=∠CDF, ∠A=∠CFD=90°及△AED≌△FDC,利用全等三角形的对应边相等,可得到ED=CD,设AE=x,利用勾股定理,建立关于x的方程,解方程求出x的值,即可得到CD的长。
9.【答案】解:∵a,b是Rt△ABC的两条直角边,c是斜边,∴a2+b2=c2,即a2=c2﹣b2=(c+b)(c﹣b),∵a为质数,∴c+b=a2,c﹣b=1,∴a2=2b+1,∴2(a+b+1)=a2+2a+1=(a+1)2,∴2(a+b+1)是完全平方数.
【解析】【分析】由勾股定理变形得a2=c2﹣b2=(c+b)(c﹣b),根据a为质数可得c+b=a2,c﹣b=1,于是可得a2=2b+1,代入2(a+b+1)可得证。
10.【答案】解:设经过x小时能赶上,则OB=75x,则AB=60x.在直角△ABC中,∵OB2=OA2+AB2,∴(75x)2=302+(60x)2,解得:x= ,故经过时间为 小时. 答:经过 小时能赶上.
【解析】【分析】 设经过x小时能赶上,则OB=75x,则AB=60x.在直角△ABC中 ,利用勾股定理建立方程,求解即可得出答案。
11.【答案】(1)证明:∵四边形ABCD是矩形,
∴AB=CD,∠A=∠C=90°,∠ABD=∠BDC,
∵△BEH是△BAH翻折而成,
∴∠ABH=∠EBH,∠A=∠HEB=90°,AB=BE,
∵△DGF是△DGC翻折而成,
∴∠FDG=∠CDG,∠C=∠DFG=90°,CD=DF,
∴∠DBH=∠ABD,∠BDG=∠BDC,
∴∠DBH=∠BDG,
∴△BEH与△DFG中,
∠HEB=∠DFG,BE=DF,∠DBH=∠BDG,
∴△BEH≌△DFG,
(2)解:∵四边形ABCD是矩形,AB=6cm,BC=8cm,
∴AB=CD=6cm,AD=BC=8cm,
∴BD===10,
∵由(1)知,FD=CD,CG=FG,
∴BF=10-6=4cm,
设FG=x,则BG=8-x,
在Rt△BGF中,
BG2=BF2+FG2,即(8-x)2=42+x2,
解得x=3,即FG=3cm.
【解析】【分析】(1)先根据矩形的性质得出∠ABD=∠BDC,再由图形折叠的性质得出∠ABH=∠EBH,∠FDG=∠CDG,∠A=∠HEB=90°,∠C=∠DFG=90°,进而可得出△BEH≌△DFG;
(2)先根据勾股定理得出BD的长,进而得出BF的长,由图形翻折变换的性质得出CG=FG,设FG=x,则BG=8-x,再利用勾股定理即可求出x的值.
12.【答案】解:如图,过点A作AE⊥BC于点E,
∵AB=AC=20,BC=32,
∴BE=CE=16,
在Rt△ACE中,利用勾股定理可知:AE= ,
设BD=x,则DE=16﹣x,DC=32﹣x,
又DA⊥CA,
在Rt△ADE和Rt△ADC中分别利用勾股定理得: ,
代入为: ,
整理得:
解得: .
即BD=7.
【解析】【分析】过点A作AE⊥BC于点E,首先根据等腰三角形的三线合一得出 BE=CE=16, 在Rt△ACE中,用勾股定理可求得AE的值,设BD=x,则DE=16﹣x,DC=32﹣x,在Rt△ADE和Rt△ADC中分别利用勾股定理可将AD2用含x的代数式表示并列出关于x的方程,解方程即可求解.
13.【答案】解:设EB′=x,
∵∠B=90°,AB=6,BC=8,
∴AC= ,
由折叠的性质可知,BE=EB′=x,AB′=AB=6,
则CB′=AC-AB′=4,EC=BC-BE=8-x,
由勾股定理得,x2+42=(8-x)2,
解得x=3,
∴EB′=3.
【解析】【分析】先利用勾股定理求出AC=10,再求出 x2+42=(8-x)2, 最后计算求解即可。
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
