12.2 三角形全等的判定(3)学案(有答案)
文档属性
| 名称 | 12.2 三角形全等的判定(3)学案(有答案) |  | |
| 格式 | zip | ||
| 文件大小 | 82.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-09-13 16:11:10 | ||
图片预览


文档简介
12.2 三角形全等的判定(3)
【学习目标】:
探索并掌握两个三角形全等的条件“ASA”、“AAS”,并能应用它们判别两个三角形是否全等.
【学习重点】:
理解掌握三角形全等的条件“ASA”、“AAS”.
【学习难点】:
探究出“ASA”、“AAS”以及它们的应用.
【课前自学、课中交流】
一.复习
(1)三角形中已知三个元素,包括哪几种情况_________、__________ 、_________、__________.
(2)到目前为止,可以作为判别两个三角形全等的方法有几种?_________.
各是什么_________、__________ .
在两个三角形中,已知三个元素相等的四种情况中,我们研究了三种,今天这节课接着探究已知两角一边对应相等是否可以判断两个三角形全等呢?
二. 新课
1.三角形中已知两角一边有哪几种可能性______________、_______________ .
2.三角形的两个内角分别是60°和45°,它们的夹边为3cm,你能画一个三角形,同时满足这些条件吗?将你画的三角形剪下,与同伴比较,观察它们是否全等,你能得出什么规律?
提炼规律:
____________________________对应相等的两个三角形全等(可以简写成“_______”或“_______”)
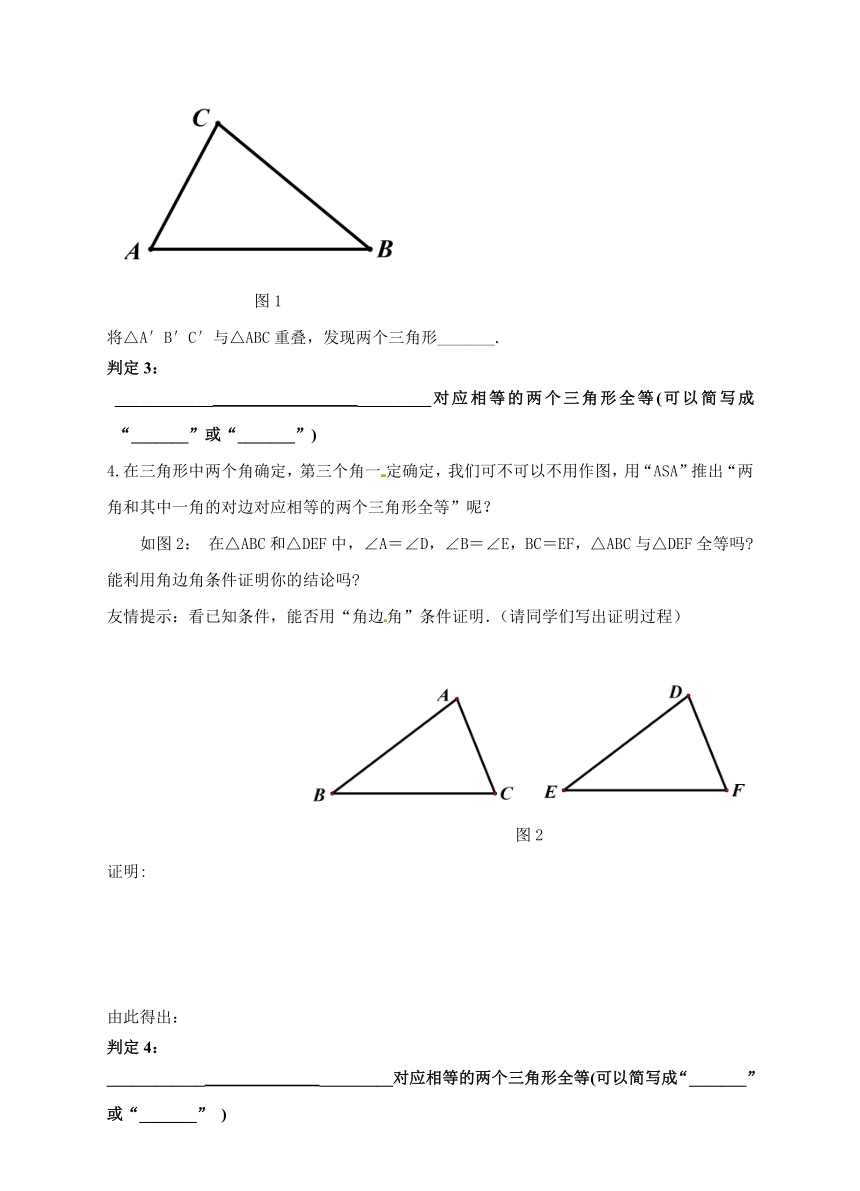
3.我们刚才画的三角形是特殊的三角形,随意画一个△ABC,如图1,能不能作一个△A′B′C′,使A′B′=AB,∠A′=∠A,∠B′=∠B呢?把画好的△A′B′C′剪下,放到△ABC上,它们全等吗 (画出图形)
图1
将△A′B′C′与△ABC重叠,发现两个三角形_______.
判定3:
____________ _________对应相等的两个三角形全等(可以简写成“_______”或“_______”)
4.在三角形中两个角确定,第三个角一定确定,我们可不可以不用作图,用“ASA”推出“两角和其中一角的对边对应相等的两个三角形全等”呢?
如图2: 在△ABC和△DEF中,∠A=∠D,∠B=∠E,BC=EF,△ABC与△DEF全等吗 能利用角边角条件证明你的结论吗
友情提示:看已知条件,能否用“角边角”条件证明.(请同学们写出证明过程)
图2
证明:
由此得出:
判定4:
____________ _________对应相等的两个三角形全等(可以简写成“_______”或“_______” )
5.例题讲解
已知:如图3,点D在AB上,点E在AC上,BE和CD相交于点O,AB=AC,∠B=∠C.
求证:AD=AE.
分析:如果能证明△ACD≌△ABE,就可以得出AD=AE.
证明:
图3
6. 三角对应相等的两个三角形全等吗 (提示:观察三角板)
结论:三角对应相等的两个三角形_______.
7.至此,已知三个条件探索三角形全等问题已全部结束,请同学们把三角形全等的判定方法做个小结.
五种判定三角形全等的条件:①全等三角形的定义、②_____ ____ 、③__ __ ____、④____ ______、⑤__________.
课堂练习:
1.如图4,小明把一块三角形的玻璃打碎成了三块,现在要到玻璃店去配一块完全一样的玻璃,那么最省事的办法( )
A、选①去 B、选②去 C、选③去 D、带①和②去
图4 图5 图6
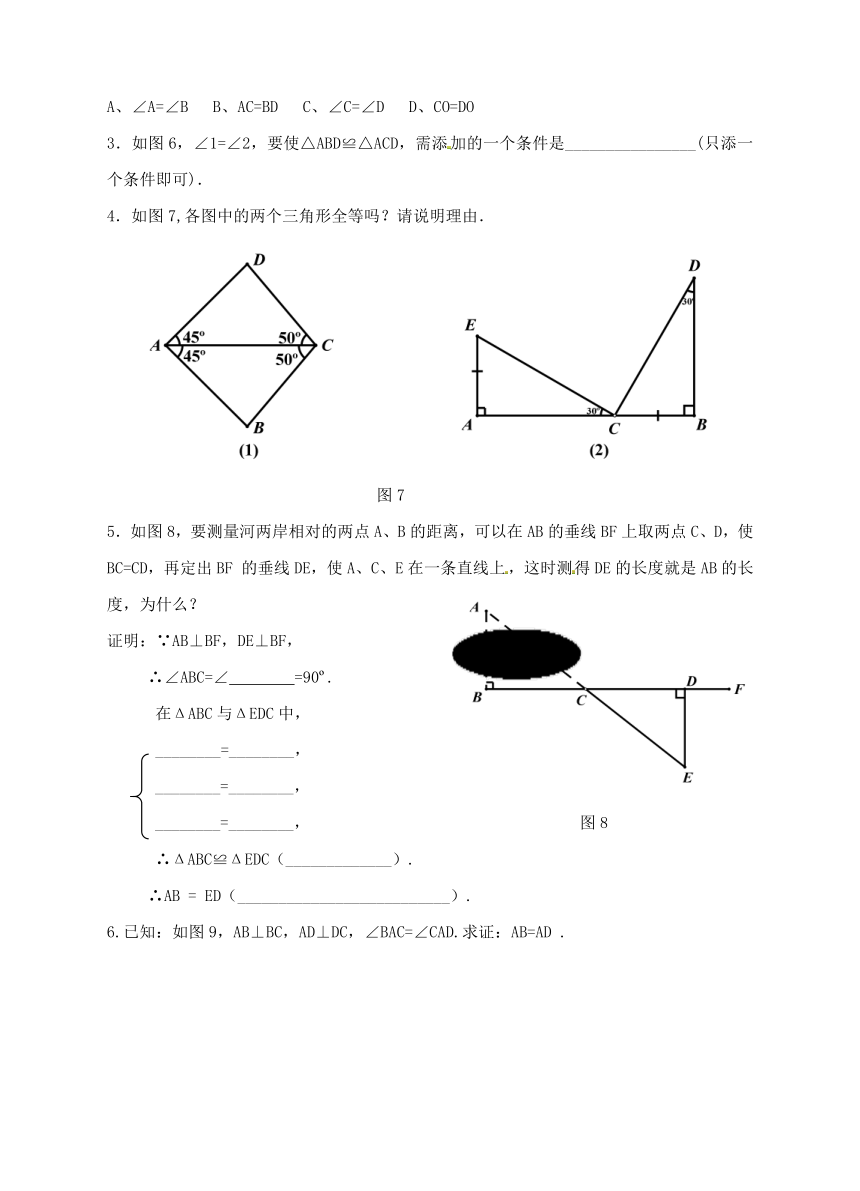
2.如图5,O是AB的中点, 要通过角边角(ASA)来判定△OAC≌△OBD,需要添加一个条件,下列条件正确的是( )
A、∠A=∠B B、AC=BD C、∠C=∠D D、CO=DO
3.如图6,∠1=∠2,要使△ABD≌△ACD,需添加的一个条件是________________(只添一个条件即可).
4.如图7,各图中的两个三角形全等吗?请说明理由.
图7
5.如图8,要测量河两岸相对的两点A、B的距离,可以在AB的垂线BF上取两点C、D,使BC=CD,再定出BF 的垂线DE,使A、C、E在一条直线上,这时测得DE的长度就是AB的长度,为什么?
证明:∵AB⊥BF,DE⊥BF,
∴∠ABC=∠ =90 .
在ΔABC与ΔEDC中,
________=________,
________=________,
________=________, 图8
∴ΔABC≌ΔEDC(_____________).
∴AB = ED(__________________________).
6.已知:如图9,AB⊥BC,AD⊥DC,∠BAC=∠CAD.求证:AB=AD .
图9
7.已知:如图10,∠1=∠2,∠3=∠4,AB与CD相等吗?请你说明理由.
图10
8.已知:如,∠1=∠2,∠3=∠4,求证:AB=AD.
图11
9. 已知:如图12,∠EBC=∠EDC,AE=AC, 求证:CB=ED.
图12
10. 已知:如图13,∠ABC=∠DCE=90°,AC⊥DE于点F ,AB=CE.求证:AC=DE.
图13
课堂练习答案:
1. C.
2. A.
3. ∠C=∠B或∠ADC=∠ADB.
4.全等,ASA;全等,AAS.
5.依次填:∠EDC,∠ABC=∠EDC,BC=CD, ∠ACB=∠ECD,ASA,全等三角形的对应边相等.
6. 证明:∵AB⊥BC,AD⊥DC,
∴∠ABC=∠ADC=90°.
在△ABC与△ADC中,
∴ △ABC≌△ADC (AAS).
∴AB=CD.
7.相等.
证明:∵∠1=∠2,∠3=∠4,
∴∠ABC=∠DCB.
在△ABC与△DCB中,
∴ △ABC≌△DCB (ASA).
∴AB=CD.
8. 证明:∵∠3=∠4,
∴∠ACB=∠ACD.
在△ABC与△ADC中,
∴ △ABC≌△ADC (AAS).
∴AB=AD.
9. 证明:∵∠EBC=∠EDC,
∴∠ABE=∠ADC.
在△ABE与△ADC中,
∴ △ABE≌△ADC (AAS).
∴AB=AD.
∵AE=AC,
∴CB=ED.
10.证明:∵AC⊥DE,
∴∠EFC=90°,
∴∠ECF+∠FEC=90°.
∵∠ABC=90°,
∴∠ECF+∠A=90°,
∴∠A=∠FEC.
在△ABC与△ECD中,
∴ △ABC≌△ECD (AAS).
∴AC=DE.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
【学习目标】:
探索并掌握两个三角形全等的条件“ASA”、“AAS”,并能应用它们判别两个三角形是否全等.
【学习重点】:
理解掌握三角形全等的条件“ASA”、“AAS”.
【学习难点】:
探究出“ASA”、“AAS”以及它们的应用.
【课前自学、课中交流】
一.复习
(1)三角形中已知三个元素,包括哪几种情况_________、__________ 、_________、__________.
(2)到目前为止,可以作为判别两个三角形全等的方法有几种?_________.
各是什么_________、__________ .
在两个三角形中,已知三个元素相等的四种情况中,我们研究了三种,今天这节课接着探究已知两角一边对应相等是否可以判断两个三角形全等呢?
二. 新课
1.三角形中已知两角一边有哪几种可能性______________、_______________ .
2.三角形的两个内角分别是60°和45°,它们的夹边为3cm,你能画一个三角形,同时满足这些条件吗?将你画的三角形剪下,与同伴比较,观察它们是否全等,你能得出什么规律?
提炼规律:
____________________________对应相等的两个三角形全等(可以简写成“_______”或“_______”)
3.我们刚才画的三角形是特殊的三角形,随意画一个△ABC,如图1,能不能作一个△A′B′C′,使A′B′=AB,∠A′=∠A,∠B′=∠B呢?把画好的△A′B′C′剪下,放到△ABC上,它们全等吗 (画出图形)
图1
将△A′B′C′与△ABC重叠,发现两个三角形_______.
判定3:
____________ _________对应相等的两个三角形全等(可以简写成“_______”或“_______”)
4.在三角形中两个角确定,第三个角一定确定,我们可不可以不用作图,用“ASA”推出“两角和其中一角的对边对应相等的两个三角形全等”呢?
如图2: 在△ABC和△DEF中,∠A=∠D,∠B=∠E,BC=EF,△ABC与△DEF全等吗 能利用角边角条件证明你的结论吗
友情提示:看已知条件,能否用“角边角”条件证明.(请同学们写出证明过程)
图2
证明:
由此得出:
判定4:
____________ _________对应相等的两个三角形全等(可以简写成“_______”或“_______” )
5.例题讲解
已知:如图3,点D在AB上,点E在AC上,BE和CD相交于点O,AB=AC,∠B=∠C.
求证:AD=AE.
分析:如果能证明△ACD≌△ABE,就可以得出AD=AE.
证明:
图3
6. 三角对应相等的两个三角形全等吗 (提示:观察三角板)
结论:三角对应相等的两个三角形_______.
7.至此,已知三个条件探索三角形全等问题已全部结束,请同学们把三角形全等的判定方法做个小结.
五种判定三角形全等的条件:①全等三角形的定义、②_____ ____ 、③__ __ ____、④____ ______、⑤__________.
课堂练习:
1.如图4,小明把一块三角形的玻璃打碎成了三块,现在要到玻璃店去配一块完全一样的玻璃,那么最省事的办法( )
A、选①去 B、选②去 C、选③去 D、带①和②去
图4 图5 图6
2.如图5,O是AB的中点, 要通过角边角(ASA)来判定△OAC≌△OBD,需要添加一个条件,下列条件正确的是( )
A、∠A=∠B B、AC=BD C、∠C=∠D D、CO=DO
3.如图6,∠1=∠2,要使△ABD≌△ACD,需添加的一个条件是________________(只添一个条件即可).
4.如图7,各图中的两个三角形全等吗?请说明理由.
图7
5.如图8,要测量河两岸相对的两点A、B的距离,可以在AB的垂线BF上取两点C、D,使BC=CD,再定出BF 的垂线DE,使A、C、E在一条直线上,这时测得DE的长度就是AB的长度,为什么?
证明:∵AB⊥BF,DE⊥BF,
∴∠ABC=∠ =90 .
在ΔABC与ΔEDC中,
________=________,
________=________,
________=________, 图8
∴ΔABC≌ΔEDC(_____________).
∴AB = ED(__________________________).
6.已知:如图9,AB⊥BC,AD⊥DC,∠BAC=∠CAD.求证:AB=AD .
图9
7.已知:如图10,∠1=∠2,∠3=∠4,AB与CD相等吗?请你说明理由.
图10
8.已知:如,∠1=∠2,∠3=∠4,求证:AB=AD.
图11
9. 已知:如图12,∠EBC=∠EDC,AE=AC, 求证:CB=ED.
图12
10. 已知:如图13,∠ABC=∠DCE=90°,AC⊥DE于点F ,AB=CE.求证:AC=DE.
图13
课堂练习答案:
1. C.
2. A.
3. ∠C=∠B或∠ADC=∠ADB.
4.全等,ASA;全等,AAS.
5.依次填:∠EDC,∠ABC=∠EDC,BC=CD, ∠ACB=∠ECD,ASA,全等三角形的对应边相等.
6. 证明:∵AB⊥BC,AD⊥DC,
∴∠ABC=∠ADC=90°.
在△ABC与△ADC中,
∴ △ABC≌△ADC (AAS).
∴AB=CD.
7.相等.
证明:∵∠1=∠2,∠3=∠4,
∴∠ABC=∠DCB.
在△ABC与△DCB中,
∴ △ABC≌△DCB (ASA).
∴AB=CD.
8. 证明:∵∠3=∠4,
∴∠ACB=∠ACD.
在△ABC与△ADC中,
∴ △ABC≌△ADC (AAS).
∴AB=AD.
9. 证明:∵∠EBC=∠EDC,
∴∠ABE=∠ADC.
在△ABE与△ADC中,
∴ △ABE≌△ADC (AAS).
∴AB=AD.
∵AE=AC,
∴CB=ED.
10.证明:∵AC⊥DE,
∴∠EFC=90°,
∴∠ECF+∠FEC=90°.
∵∠ABC=90°,
∴∠ECF+∠A=90°,
∴∠A=∠FEC.
在△ABC与△ECD中,
∴ △ABC≌△ECD (AAS).
∴AC=DE.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
