数学人教A版(2019)必修第一册5.4.2正弦函数、余弦函数的性质 课件(共42张ppt)
文档属性
| 名称 | 数学人教A版(2019)必修第一册5.4.2正弦函数、余弦函数的性质 课件(共42张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 2.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-18 09:10:46 | ||
图片预览










文档简介
(共42张PPT)
正弦函数、余弦函数的性质
新课程标准 核心素养
1.了解周期函数的概念、正弦函数与余弦函数的周期性,会求函数的周期. 数学抽象
数学运算
2.了解三角函数的奇偶性以及对称性,会判断给定函数的奇偶性. 直观想象
逻辑推理
3.了解正弦函数与余弦函数的单调性,并会利用函数单调性求函数的最值和值域. 数学抽象数学运算
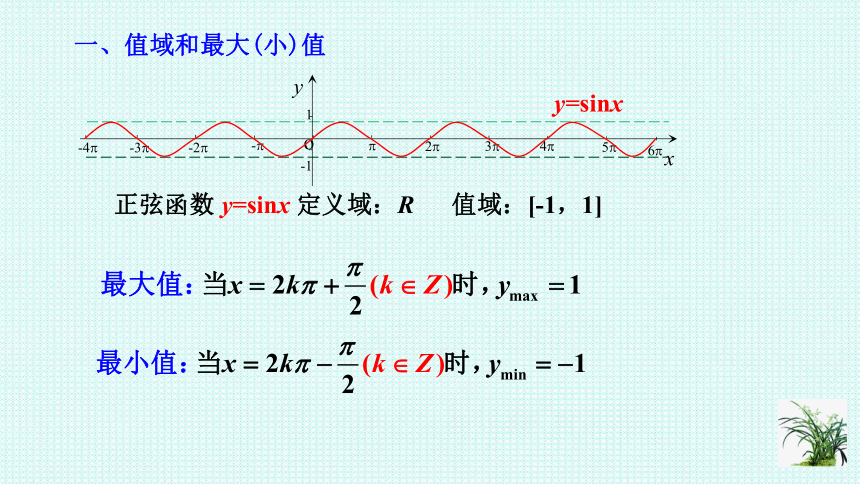
一、值域和最大(小)值
x
6
y
o
-
-1
2
3
4
5
-2
-3
-4
1
y=sinx
正弦函数 y=sinx 定义域:R 值域:[-1,1]
x
6
y
o
-
-1
2
3
4
5
-2
-3
-4
1
y=cosx
余弦函数 y=cosx 定义域:R 值域:[-1,1]
令3x+ =
π
3
2kπ+
π
2
x= + (k∈Z )时,ymax=2
2kπ
3
π
18
令3x+ =
π
3
2kπ -
π
2
x= - (k∈Z )时,ymin=-2
2kπ
3
5π
18
令2x+ =2kπ
π
6
x= kπ- (k∈Z )时,ymin=-2
π
12
x=kπ + (k∈Z )时,ymax=4
5π
12
二.周期函数的概念
由正、余弦函数的图象可知, 正、余弦曲线每相隔2π个单位重复出现, 这一规律的理论依据是什么?
sin(x+2kπ)=sinx cos(x+2kπ)=cosx
若f(x)=sinx,则 f(x+2kπ)=f(x)
当任意自变量x的值增加2kπ(k∈Z)时,函数值会重复出现.函数的这种特性叫做周期性。
正弦函数f(x)=sinx、余弦函数f(x)=cosx都是周期函数.
周期函数的定义:
对于函数f(x),如果存在一个_____ __ T,使得当x取定义域内的
___ ___ 值时,都有___ _______ 那么函数f(x)就叫做周期函数,
非零常数T就叫做这个函数的周期.
非零常数
每一个
f(x+T)=f(x)
最小正周期的定义: 如果在周期函数f(x)的所有周期中存在一个最小的正数,则这个最小正数叫做f(x)的最小正周期.
正、余弦函数是周期函数,2kπ(k∈Z, k≠0)都是它的周期,最小正周期是2π.
说明
1.周期T应该是非零常数.可以是正数,也可以是负数.
2.周期函数f(x+T)=f(x)对定义域中每个x值都恒成立.
3.对于f(x+T)=f(x),自变量本身加的常数才是周期.
4.周期函数的周期不止一个. (若T是f(x)的一个周期,则kT(k∈Z且k≠0)都是f(x)的周期)
问题1:等式sin(300+1200)=sin300成立,能否说明1200是正弦函数y=sinx, x∈R的一个周期?为什么?
不能!因为sin(x+1200)=sinx并不对任意x∈R都成立。
问题2:判断下列说法是否正确?
①如果f(x+2kπ)=f(x)(k∈Z),那么2kπ是函数f(x)的周期( )
②函数f(x)=sinx(x∈[0,4π])是周期函数 ( )
③所有周期函数都有最小正周期 ( )
╳
╳
╳
任意性
非零性
多值性
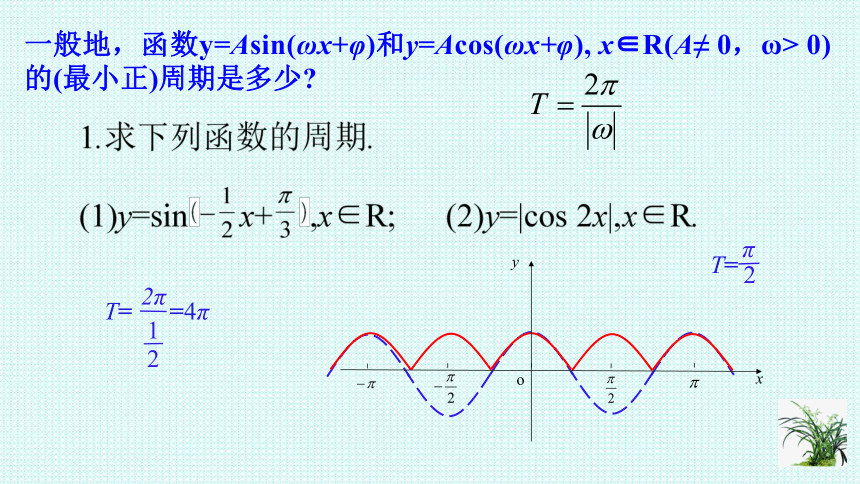
例1. 求下列函数的周期:
⑴y=3cosx,x∈R; ⑵y=sin2x,x∈R;
∵ 3cos(x+2π)= 3cosx , ∴周期为2π.
∵sin2(x+π)=sin(2x+2π)=sin2x, ∴函数的周期为π.
解 :(3)令 ,由x∈R得z∈R,且y=2sin z的周期为2π
于是 ,
所以 ,x∈R.
原函数的周期为4π
一般地,函数y=Asin(ωx+φ)和y=Acos(ωx+φ), x∈R(A≠ 0,ω> 0)的(最小正)周期是多少
T= =4π
2π
1
2
o
y
x
T=
π
2
解析:易知f(x)的最小正周期T=6,则有
f(0)+f(1)+f(2)+f(3)+f(4)+f(5)=0.
则f(0)+f(1)+…+f(13)=2[f(0)+f(1)+f(2)+f(3)+f(4)+f(5)]+f(12)+f(13)=f(12)+f(13)=f(0)+f(1)=2+1=3.
例2.设f(x)是定义在R上的奇函数,且对任意实数x,恒有f(x+2)=-f(x).当x∈[0,2]时,f(x)=2x-x2.
①求函数的最小正周期;
②计算f(0)+f(1)+f(2)+…+f(2 017).
[解] ①∵f(x+2)=-f(x),∴f(x+4)=-f(x+2)=f(x).
∴f(x)的最小正周期为4.
②f(0)=0,f(1)=1,f(2)=0,
f(3)=f(-1)=-f(1)=-1. 又f(x)是周期为4的周期函数,
∴f(0)+f(1)+f(2)+f(3)=f(4)+f(5)+f(6)+f(7)=…=f(2 012)+f(2 013)+f(2 014)+f(2 015)=0,
f(2016)=f(0)=0,f(2 017)=f(1)=1,∴f(0)+f(1)+f(2)+…+f(2 017)=1
f( )=f( +3)=-1
5
2
1
2
利用周期将所求的往已知区间转化
三.正弦函数、余弦函数的奇偶性
y=sinx,x∈R,定义域关于原点对称,f(-x)=-f(x)
正弦函数y=sinx是奇函数
1.观察正弦曲线和余弦曲线的对称性,你有什么发现?
x
6
y
o
-
-1
2
3
4
5
-2
-3
-4
1
正弦曲线关于原点O对称
x
6
y
o
-
-1
2
3
4
5
-2
-3
-4
1
y=cosx,x∈R,定义域关于原点对称,f(-x)= f(x)
余弦函数y=cosx是偶函数
余弦曲线关于y轴对称
判断下列函数的奇偶性
(1)已知x∈R ,所以定义域关于原点对称
f(-x)=-sin(-3x)=sin3x=-f(x),为奇函数
(2)已知x∈R ,所以定义域关于原点对称
f(-x)=sin(-x)+1=-sinx+1,非奇非偶
(3)已知x∈R ,所以定义域关于原点对称
f(-x)= =
cos(-x)
cosx
偶函数
o
y
x
o
y
x
o
y
x
o
y
x
正弦函数、余弦函数的性质(二)
一、正弦函数的单调性
结论:
正弦函数在每个闭区间
都是增函数,其值从-1增大到1;
而在每个闭区间
上都是
减函数,其值从1减小到-1。
二、余弦函数的单调性
结论:
在每个闭区间
都是增函数,
其值从-1增大到1 ;
在每个闭区间
上都是减函数,
其值从1减小到-1。
正弦函数基本单调增区间
[- , ]
π
2
π
2
正弦函数基本单调减区间
[ , ]
π
2
3π
2
余弦函数基本单调减区间
[0,π ]
余弦函数基本单调增区间
[-π,0 ]
基本单调区间+2kπ
例1 比较下列各组数的大小:
sin(- )>sin(- )
π
18
π
10
cos(- )=
23π
5
cos( )=
23π
5
cos
3π
5
cos(- )=
17π
4
cos( )=
17π
4
cos
π
4
∵ 0 < < < π
π
4
3π
5
cos
π
4
cos
3π
5
>
cos(- )
17π
4
cos(- )
23π
5
>
(1)∵sin(-320°)=sin(-360°+40°)=sin 40°,
sin 700°=sin(720°-20°)=sin(-20°),
又函数y=sin x在[-90°,90°]上是增函数,
∴sin 40°>sin(-20°),即sin(-320°)>sin 700°.
cos =
17π
8
cos
π
8
cos =
37π
9
cos
π
9
∴当原函数单调递减时,可得
函数y= (cos 2x)的单调递增区间.
log
1
2
由题意得cos 2x>0且y=cos 2x递减.
o
x
y
求函数y= (cos 2x)的单调递增区间.
log
1
2
(kπ, kπ+ ) (k∈Z )
π
4
求形如y=asinx+b的函数的最值或值域时,要注意a的正负
可利用正弦函数的有界性(-1≤sinx≤1)求解.
因为-1≤sinx≤1,所以
求形如y=asin2x+bsinx+c,a≠0,x∈R的函数的值域或最值时,可以通过换元,令t=sinx,将原函数转化为关于t的二次函数,利用配方法求值域或最值,求解过程中要注意正弦函数的有界性.
由x的范围,求出整体角的范围
三、正弦、余弦函数的对称性
正弦函数的对称性
x
y
o
-
-1
2
3
4
-2
-3
1
与x轴交点
过最高(低)点
余弦函数的对称性
y
x
o
-
-1
2
3
4
-2
-3
1
任意两相邻对称轴(或对称中心)的间距为半个周期;
对称轴与其相邻的对称中心的间距为四分之一个周期
例5:求函数 的对称轴和对称中心
解:(1)令 ,则 y = sin( )=sinz
z =2x+
π
3
2x+
π
3
y=sinz对称轴z= (k∈Z )
kπ+
π
2
2x+ =
π
3
kπ+
π
2
对称轴 x= + (k∈Z )
kπ
2
π
12
y=sinz对称(kπ,0)k∈Z,
2x+ =kπ,
π
3
x= - (k∈Z ),对称中心( - ,0)(k∈Z )
kπ
2
π
6
kπ
2
π
6
+φ=
2π
3
kπ+
π
2
φ=kπ- (k∈Z )
π
6
+φ=
π
4
kπ+
π
2
φ=kπ + (k∈Z )
π
4
ω=2,
2x+ =kπ
π
3
2× +φ = (k∈Z )
π
6
2kπ+
π
2
归纳:三角函数中心对称与轴对称问题:
正弦函数、余弦函数的性质
新课程标准 核心素养
1.了解周期函数的概念、正弦函数与余弦函数的周期性,会求函数的周期. 数学抽象
数学运算
2.了解三角函数的奇偶性以及对称性,会判断给定函数的奇偶性. 直观想象
逻辑推理
3.了解正弦函数与余弦函数的单调性,并会利用函数单调性求函数的最值和值域. 数学抽象数学运算
一、值域和最大(小)值
x
6
y
o
-
-1
2
3
4
5
-2
-3
-4
1
y=sinx
正弦函数 y=sinx 定义域:R 值域:[-1,1]
x
6
y
o
-
-1
2
3
4
5
-2
-3
-4
1
y=cosx
余弦函数 y=cosx 定义域:R 值域:[-1,1]
令3x+ =
π
3
2kπ+
π
2
x= + (k∈Z )时,ymax=2
2kπ
3
π
18
令3x+ =
π
3
2kπ -
π
2
x= - (k∈Z )时,ymin=-2
2kπ
3
5π
18
令2x+ =2kπ
π
6
x= kπ- (k∈Z )时,ymin=-2
π
12
x=kπ + (k∈Z )时,ymax=4
5π
12
二.周期函数的概念
由正、余弦函数的图象可知, 正、余弦曲线每相隔2π个单位重复出现, 这一规律的理论依据是什么?
sin(x+2kπ)=sinx cos(x+2kπ)=cosx
若f(x)=sinx,则 f(x+2kπ)=f(x)
当任意自变量x的值增加2kπ(k∈Z)时,函数值会重复出现.函数的这种特性叫做周期性。
正弦函数f(x)=sinx、余弦函数f(x)=cosx都是周期函数.
周期函数的定义:
对于函数f(x),如果存在一个_____ __ T,使得当x取定义域内的
___ ___ 值时,都有___ _______ 那么函数f(x)就叫做周期函数,
非零常数T就叫做这个函数的周期.
非零常数
每一个
f(x+T)=f(x)
最小正周期的定义: 如果在周期函数f(x)的所有周期中存在一个最小的正数,则这个最小正数叫做f(x)的最小正周期.
正、余弦函数是周期函数,2kπ(k∈Z, k≠0)都是它的周期,最小正周期是2π.
说明
1.周期T应该是非零常数.可以是正数,也可以是负数.
2.周期函数f(x+T)=f(x)对定义域中每个x值都恒成立.
3.对于f(x+T)=f(x),自变量本身加的常数才是周期.
4.周期函数的周期不止一个. (若T是f(x)的一个周期,则kT(k∈Z且k≠0)都是f(x)的周期)
问题1:等式sin(300+1200)=sin300成立,能否说明1200是正弦函数y=sinx, x∈R的一个周期?为什么?
不能!因为sin(x+1200)=sinx并不对任意x∈R都成立。
问题2:判断下列说法是否正确?
①如果f(x+2kπ)=f(x)(k∈Z),那么2kπ是函数f(x)的周期( )
②函数f(x)=sinx(x∈[0,4π])是周期函数 ( )
③所有周期函数都有最小正周期 ( )
╳
╳
╳
任意性
非零性
多值性
例1. 求下列函数的周期:
⑴y=3cosx,x∈R; ⑵y=sin2x,x∈R;
∵ 3cos(x+2π)= 3cosx , ∴周期为2π.
∵sin2(x+π)=sin(2x+2π)=sin2x, ∴函数的周期为π.
解 :(3)令 ,由x∈R得z∈R,且y=2sin z的周期为2π
于是 ,
所以 ,x∈R.
原函数的周期为4π
一般地,函数y=Asin(ωx+φ)和y=Acos(ωx+φ), x∈R(A≠ 0,ω> 0)的(最小正)周期是多少
T= =4π
2π
1
2
o
y
x
T=
π
2
解析:易知f(x)的最小正周期T=6,则有
f(0)+f(1)+f(2)+f(3)+f(4)+f(5)=0.
则f(0)+f(1)+…+f(13)=2[f(0)+f(1)+f(2)+f(3)+f(4)+f(5)]+f(12)+f(13)=f(12)+f(13)=f(0)+f(1)=2+1=3.
例2.设f(x)是定义在R上的奇函数,且对任意实数x,恒有f(x+2)=-f(x).当x∈[0,2]时,f(x)=2x-x2.
①求函数的最小正周期;
②计算f(0)+f(1)+f(2)+…+f(2 017).
[解] ①∵f(x+2)=-f(x),∴f(x+4)=-f(x+2)=f(x).
∴f(x)的最小正周期为4.
②f(0)=0,f(1)=1,f(2)=0,
f(3)=f(-1)=-f(1)=-1. 又f(x)是周期为4的周期函数,
∴f(0)+f(1)+f(2)+f(3)=f(4)+f(5)+f(6)+f(7)=…=f(2 012)+f(2 013)+f(2 014)+f(2 015)=0,
f(2016)=f(0)=0,f(2 017)=f(1)=1,∴f(0)+f(1)+f(2)+…+f(2 017)=1
f( )=f( +3)=-1
5
2
1
2
利用周期将所求的往已知区间转化
三.正弦函数、余弦函数的奇偶性
y=sinx,x∈R,定义域关于原点对称,f(-x)=-f(x)
正弦函数y=sinx是奇函数
1.观察正弦曲线和余弦曲线的对称性,你有什么发现?
x
6
y
o
-
-1
2
3
4
5
-2
-3
-4
1
正弦曲线关于原点O对称
x
6
y
o
-
-1
2
3
4
5
-2
-3
-4
1
y=cosx,x∈R,定义域关于原点对称,f(-x)= f(x)
余弦函数y=cosx是偶函数
余弦曲线关于y轴对称
判断下列函数的奇偶性
(1)已知x∈R ,所以定义域关于原点对称
f(-x)=-sin(-3x)=sin3x=-f(x),为奇函数
(2)已知x∈R ,所以定义域关于原点对称
f(-x)=sin(-x)+1=-sinx+1,非奇非偶
(3)已知x∈R ,所以定义域关于原点对称
f(-x)= =
cos(-x)
cosx
偶函数
o
y
x
o
y
x
o
y
x
o
y
x
正弦函数、余弦函数的性质(二)
一、正弦函数的单调性
结论:
正弦函数在每个闭区间
都是增函数,其值从-1增大到1;
而在每个闭区间
上都是
减函数,其值从1减小到-1。
二、余弦函数的单调性
结论:
在每个闭区间
都是增函数,
其值从-1增大到1 ;
在每个闭区间
上都是减函数,
其值从1减小到-1。
正弦函数基本单调增区间
[- , ]
π
2
π
2
正弦函数基本单调减区间
[ , ]
π
2
3π
2
余弦函数基本单调减区间
[0,π ]
余弦函数基本单调增区间
[-π,0 ]
基本单调区间+2kπ
例1 比较下列各组数的大小:
sin(- )>sin(- )
π
18
π
10
cos(- )=
23π
5
cos( )=
23π
5
cos
3π
5
cos(- )=
17π
4
cos( )=
17π
4
cos
π
4
∵ 0 < < < π
π
4
3π
5
cos
π
4
cos
3π
5
>
cos(- )
17π
4
cos(- )
23π
5
>
(1)∵sin(-320°)=sin(-360°+40°)=sin 40°,
sin 700°=sin(720°-20°)=sin(-20°),
又函数y=sin x在[-90°,90°]上是增函数,
∴sin 40°>sin(-20°),即sin(-320°)>sin 700°.
cos =
17π
8
cos
π
8
cos =
37π
9
cos
π
9
∴当原函数单调递减时,可得
函数y= (cos 2x)的单调递增区间.
log
1
2
由题意得cos 2x>0且y=cos 2x递减.
o
x
y
求函数y= (cos 2x)的单调递增区间.
log
1
2
(kπ, kπ+ ) (k∈Z )
π
4
求形如y=asinx+b的函数的最值或值域时,要注意a的正负
可利用正弦函数的有界性(-1≤sinx≤1)求解.
因为-1≤sinx≤1,所以
求形如y=asin2x+bsinx+c,a≠0,x∈R的函数的值域或最值时,可以通过换元,令t=sinx,将原函数转化为关于t的二次函数,利用配方法求值域或最值,求解过程中要注意正弦函数的有界性.
由x的范围,求出整体角的范围
三、正弦、余弦函数的对称性
正弦函数的对称性
x
y
o
-
-1
2
3
4
-2
-3
1
与x轴交点
过最高(低)点
余弦函数的对称性
y
x
o
-
-1
2
3
4
-2
-3
1
任意两相邻对称轴(或对称中心)的间距为半个周期;
对称轴与其相邻的对称中心的间距为四分之一个周期
例5:求函数 的对称轴和对称中心
解:(1)令 ,则 y = sin( )=sinz
z =2x+
π
3
2x+
π
3
y=sinz对称轴z= (k∈Z )
kπ+
π
2
2x+ =
π
3
kπ+
π
2
对称轴 x= + (k∈Z )
kπ
2
π
12
y=sinz对称(kπ,0)k∈Z,
2x+ =kπ,
π
3
x= - (k∈Z ),对称中心( - ,0)(k∈Z )
kπ
2
π
6
kπ
2
π
6
+φ=
2π
3
kπ+
π
2
φ=kπ- (k∈Z )
π
6
+φ=
π
4
kπ+
π
2
φ=kπ + (k∈Z )
π
4
ω=2,
2x+ =kπ
π
3
2× +φ = (k∈Z )
π
6
2kπ+
π
2
归纳:三角函数中心对称与轴对称问题:
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
