人教版九年级上册 24.2.1 点与圆的位置关系(第2课时)课件(共14张PPT)
文档属性
| 名称 | 人教版九年级上册 24.2.1 点与圆的位置关系(第2课时)课件(共14张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-19 00:00:00 | ||
图片预览





文档简介
(共15张PPT)
学习目标
1.巩固点和圆的位置关系;
2.掌握反证法;
3.体会分类讨论及数形结合的思想;
4.体验探索数学的乐趣.
1. ⊙O的直径8cm,点P为线段OA的中点,若线段OA=12cm,则点P在⊙O ;
若线段OA=8cm,则点P在⊙O ;
若线段OA=5cm,则点P在⊙O .
2.⊙O的半径6cm,当OP=6cm时,点P在 ;当OP 时点P在圆内;当OP 时,点P不在圆外.
圆内
圆上
圆外
圆上
<6cm
≤6cm
温故知新
3. ⊙O的半径r=10cm,圆心到直线l的距离OM=8cm,在直线l 上有一点P,PM=6cm,则点P( )
A. 在⊙O内 B. 在⊙O 外
C. 在⊙O上 D. 不能确定
4. ⊙O的半径为6,圆心O的坐标(0,0) ,点P的坐标为(4,5),则点P与⊙O的位置关系是 ( )
A. 在⊙O内 B. 在⊙O 外
C. 在⊙O上 D. 在⊙O 上或⊙O内
C
B
温故知新
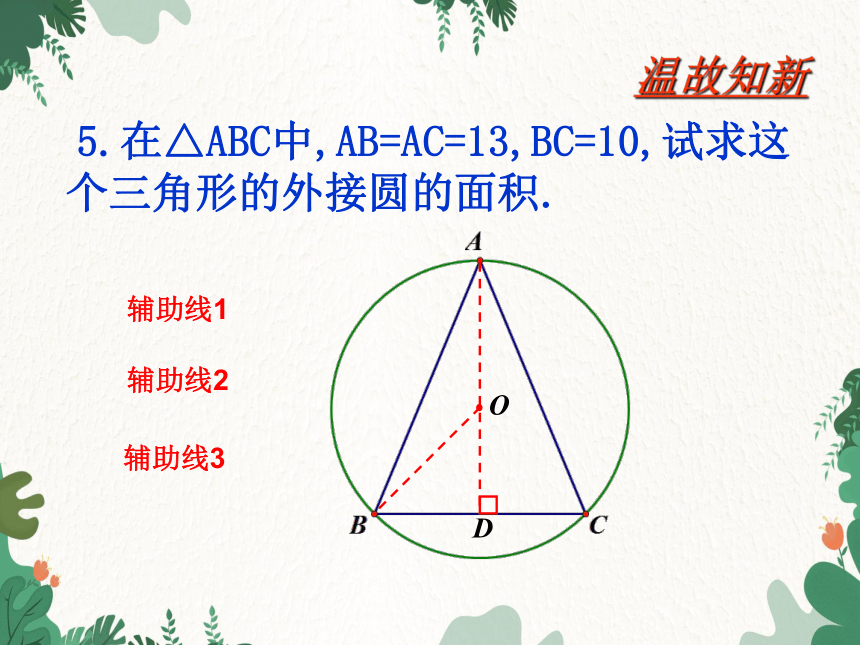
5.在△ABC中,AB=AC=13,BC=10,试求这个三角形的外接圆的面积.
温故知新
D
O
辅助线1
辅助线2
辅助线3
求证:过同一直线上的三点不能作圆.
A
B
C
已知:点A、B、C在直线l上
求证:过A、B、C三点不能作圆.
问题探究
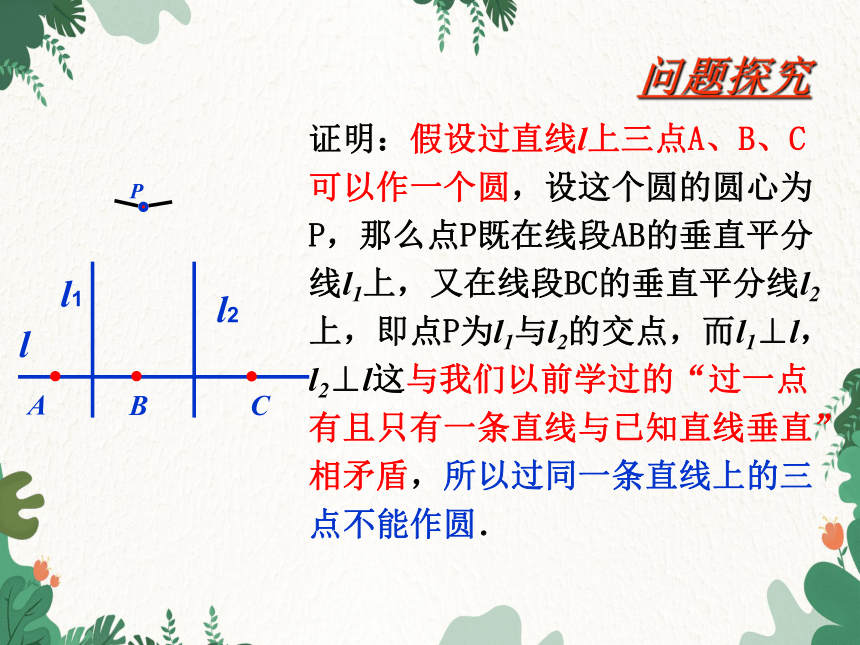
证明:假设过直线l上三点A、B、C可以作一个圆,设这个圆的圆心为P,那么点P既在线段AB的垂直平分线l1上,又在线段BC的垂直平分线l2上,即点P为l1与l2的交点,而l1⊥l,l2⊥l这与我们以前学过的“过一点有且只有一条直线与已知直线垂直”相矛盾,所以过同一条直线上的三点不能作圆.
l1
l2
A
B
C
P
l
问题探究
先假设命题的结论不成立,然后由此经过推理得出矛盾(常与公理、定理、定义或已知条件相矛盾),由矛盾判定假设不正确,从而得到原命题成立,这种方法叫做反证法.
什么叫反证法?
规律归纳
用反证法证明一个命题,一般有三个步骤:
1.提出假设---假设原命题不成立,即提出一个与原命题相反的命题;
2.推出矛盾---从假设出发,推出一个与已知条件或定义、定理、公理相矛盾的结果;
3.推翻假设,命题得证---从矛盾推翻最初提出的假设,从而原命题成立.
规律归纳
反证法常用于解决用直接证法不易证明或不能证明的命题,主要有:
(1)命题的结论是否定型的;
(2)命题的结论是无限型的;
(3)命题的结论是“至多”或“至少”型的.
规律归纳
应用举例
例.已知:m是整数,且m2是偶数 .
求证: m一定是偶数.
证明:
用反证法证明:
1.在一个三角形中,至多有一个角是直角.
巩固训练
2.已知:a∥c, b∥c,求证: a∥b.
课堂小结
2.用反证法证明一个命题有几个步骤?
1.什么叫反证法?
3.反证法的适用范围?
(1)提出假设
(2)推出矛盾
(3)推翻假设,命题得证
作业本:
用反证法证明“两直线平行,同位角相等”.
作业
学习目标
1.巩固点和圆的位置关系;
2.掌握反证法;
3.体会分类讨论及数形结合的思想;
4.体验探索数学的乐趣.
1. ⊙O的直径8cm,点P为线段OA的中点,若线段OA=12cm,则点P在⊙O ;
若线段OA=8cm,则点P在⊙O ;
若线段OA=5cm,则点P在⊙O .
2.⊙O的半径6cm,当OP=6cm时,点P在 ;当OP 时点P在圆内;当OP 时,点P不在圆外.
圆内
圆上
圆外
圆上
<6cm
≤6cm
温故知新
3. ⊙O的半径r=10cm,圆心到直线l的距离OM=8cm,在直线l 上有一点P,PM=6cm,则点P( )
A. 在⊙O内 B. 在⊙O 外
C. 在⊙O上 D. 不能确定
4. ⊙O的半径为6,圆心O的坐标(0,0) ,点P的坐标为(4,5),则点P与⊙O的位置关系是 ( )
A. 在⊙O内 B. 在⊙O 外
C. 在⊙O上 D. 在⊙O 上或⊙O内
C
B
温故知新
5.在△ABC中,AB=AC=13,BC=10,试求这个三角形的外接圆的面积.
温故知新
D
O
辅助线1
辅助线2
辅助线3
求证:过同一直线上的三点不能作圆.
A
B
C
已知:点A、B、C在直线l上
求证:过A、B、C三点不能作圆.
问题探究
证明:假设过直线l上三点A、B、C可以作一个圆,设这个圆的圆心为P,那么点P既在线段AB的垂直平分线l1上,又在线段BC的垂直平分线l2上,即点P为l1与l2的交点,而l1⊥l,l2⊥l这与我们以前学过的“过一点有且只有一条直线与已知直线垂直”相矛盾,所以过同一条直线上的三点不能作圆.
l1
l2
A
B
C
P
l
问题探究
先假设命题的结论不成立,然后由此经过推理得出矛盾(常与公理、定理、定义或已知条件相矛盾),由矛盾判定假设不正确,从而得到原命题成立,这种方法叫做反证法.
什么叫反证法?
规律归纳
用反证法证明一个命题,一般有三个步骤:
1.提出假设---假设原命题不成立,即提出一个与原命题相反的命题;
2.推出矛盾---从假设出发,推出一个与已知条件或定义、定理、公理相矛盾的结果;
3.推翻假设,命题得证---从矛盾推翻最初提出的假设,从而原命题成立.
规律归纳
反证法常用于解决用直接证法不易证明或不能证明的命题,主要有:
(1)命题的结论是否定型的;
(2)命题的结论是无限型的;
(3)命题的结论是“至多”或“至少”型的.
规律归纳
应用举例
例.已知:m是整数,且m2是偶数 .
求证: m一定是偶数.
证明:
用反证法证明:
1.在一个三角形中,至多有一个角是直角.
巩固训练
2.已知:a∥c, b∥c,求证: a∥b.
课堂小结
2.用反证法证明一个命题有几个步骤?
1.什么叫反证法?
3.反证法的适用范围?
(1)提出假设
(2)推出矛盾
(3)推翻假设,命题得证
作业本:
用反证法证明“两直线平行,同位角相等”.
作业
同课章节目录
