数学人教A版2019必修第一册2.1等式性质与不等式性质 课件(共26张ppt)
文档属性
| 名称 | 数学人教A版2019必修第一册2.1等式性质与不等式性质 课件(共26张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 772.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-18 00:00:00 | ||
图片预览








文档简介
(共26张PPT)
2.1等式性质与不等式性质
第 2 章一元二次函数、方程和不等式
人教A版2019必修第一册
学习目标
1. 了解不等式的意义,能用不等式(组)表示实际问题中的不等关系.
2. 会用作差法比较两个代数式的大小关系.(重点)
3. 掌握并会应用重要不等式.(重难点)
1. 不等关系与不等式
在现实世界和日常生活中,大量存在着相等关系和不等关系,例如多与少、
大与小、长与短、高与矮、远与近、快与慢、涨与跌、轻与重、不超过和不
少于等。类似于这样的问题反映在数量关系上就是相等和不相等,相等用等
式表示不等用不等式表示。
【等式】指的是用等号“=”连接起来的式子
【不等式】指的是用不等号“≠”“>”“<”“≥”“≤”
连接起来的式子
概念
【问题1】你能用不等式或不等式组表示下列问题中的不等关系吗?
(1)某路段限速;;
(2)某品牌酸奶的质量检查规定,酸奶中脂肪的含量应不少于2.5%,蛋
白质的含量应不少于2.3%;
(3)三角形两边之和大于第三边,两边之差小于第三边;
(4)连接直线外一点与直线上各点的所有线段中,垂线段最短.
设该路段行驶的汽车速度为,则
,
设三角形三边分别为,则
设P是直线AB外任意一点,PQ是P到AB的垂
线段,C是直线AB上任意一点,则PC≥PQ
A
B
C
P
Q
【问题2】某种杂志原以每本2.5元的价格销售,可以售出
8万本.根据市场调查,若单价每提高0.1元,销售量就可
能相应减少2 000本,若把提价后杂志的定价设为x元,怎
样用不等式表示销售的总收入仍不低于20万元?
1.某工厂在招标会上,购得甲材料x t,乙材料y t,若维持工厂正常生产,甲、乙两种材料总量至少需要120 t,则x、y应满足的不等关系是( )
A.x+y>120
B.x+y<120
C.x+y≥120
D.x+y≤120
C
[解析] 由题意可得x+y≥120,故选C.
练一练
2. 比较两个实数的大小
【问题3】
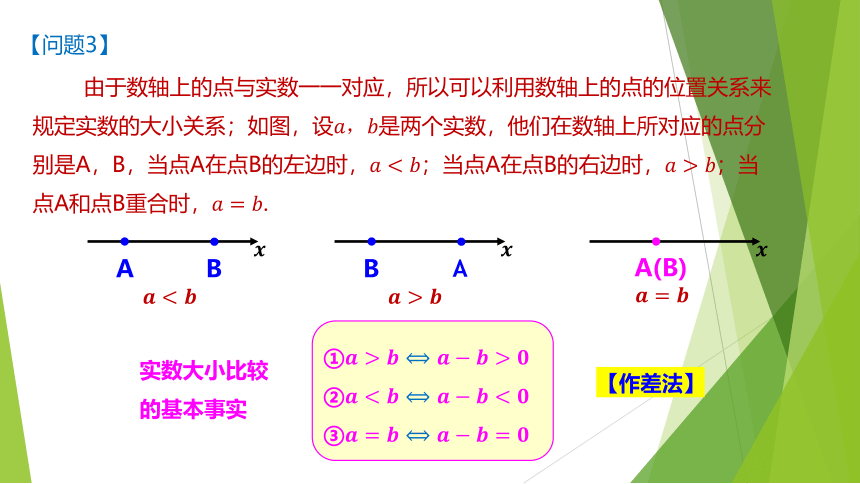
由于数轴上的点与实数一一对应,所以可以利用数轴上的点的位置关系来
规定实数的大小关系;如图,设是两个实数,他们在数轴上所对应的点分
别是A,B,当点A在点B的左边时,;当点A在点B的右边时,;当
点A和点B重合时,.
A
B
B
A
A(B)
实数大小比较
的基本事实
【作差法】
①
②
③
例1:比较和的大小.
【解】运用作差法:
2>0,
>
作差
变形
定号
定论
0是相等与不等的分界线,它也为比较实数的大小提供了标杆.
典例1
【解】运用作差法:
练一练
3.已知x<y<0,比较(x2+y2)(x-y)与
(x2-y2)(x+y)的大小.
[解析] ∵x<y<0,xy>0,x-y<0,
∴(x2+y2)(x-y)-(x2-y2)(x+y)=-2xy(x-y)>0,
∴(x2+y2)(x-y)>(x2-y2)(x+y).
练一练
3. 重要不等式
若设直角三角形的两直角边分别为a,b,则
S大于S',即
A
B
C
D
E(FGH)
当a=b时,S=S',即
A
B
C
D
E
F
G
H
a
b
当a=b时
综上,
(1)正方形ABCD的面积S=________;
四个直角三角形的面积和S' =_____;
(2) S与S’有什么样的不等关系,如何表示?
(3)S与S’会出现相等的情况吗,什么时候相等?
【问题4】
【问题5】 :如何证明重要不等式?
证明:
重要不等式
【证】:
典例1
4.设M=x2,N=-x-1,则M与N的大小关系是 ( )
A.M>N B.M=N
C.MA
练一练
[解析] 2. x2+y2+1-2(x+y-1)
=x2-2x+1+y2-2y+2
=(x-1)2+(y-1)2+1>0,
∴x2+y2+1>2(x+y-1).
5.比较x2+y2+1与2(x+y-1)的大小;
练一练
课堂练习
1.完成一项装修工程,请木工需付工资每人500元,请瓦工需付工资每人400元,现有工人工资预算20 000元,设木工x(x≥0)人,瓦工y(y≥0)人,则关于工资x,y满足的不等关系是( )
A.5x+4y<200 B.5x+4y≥200
C.5x+4y=200 D.5x+4y≤200
D
A
3.已知甲、乙两种食物的维生素A,B含量如下表:
设用x kg的甲种食物与y kg的乙种食物配成混合食物,并使混合食物内至少含有56 000单位的维生素A和63 000 单位的维生素B.试用不等式组表示x,y所满足的不等关系.
4.将一个三边长度分别为5,12,13的三角形的各边都缩短x,构成一个钝角三角形,试用不等式(组)表示x应满足的不等关系.
2.1等式性质与不等式性质
第 2 章一元二次函数、方程和不等式
人教A版2019必修第一册
学习目标
1. 了解不等式的意义,能用不等式(组)表示实际问题中的不等关系.
2. 会用作差法比较两个代数式的大小关系.(重点)
3. 掌握并会应用重要不等式.(重难点)
1. 不等关系与不等式
在现实世界和日常生活中,大量存在着相等关系和不等关系,例如多与少、
大与小、长与短、高与矮、远与近、快与慢、涨与跌、轻与重、不超过和不
少于等。类似于这样的问题反映在数量关系上就是相等和不相等,相等用等
式表示不等用不等式表示。
【等式】指的是用等号“=”连接起来的式子
【不等式】指的是用不等号“≠”“>”“<”“≥”“≤”
连接起来的式子
概念
【问题1】你能用不等式或不等式组表示下列问题中的不等关系吗?
(1)某路段限速;;
(2)某品牌酸奶的质量检查规定,酸奶中脂肪的含量应不少于2.5%,蛋
白质的含量应不少于2.3%;
(3)三角形两边之和大于第三边,两边之差小于第三边;
(4)连接直线外一点与直线上各点的所有线段中,垂线段最短.
设该路段行驶的汽车速度为,则
,
设三角形三边分别为,则
设P是直线AB外任意一点,PQ是P到AB的垂
线段,C是直线AB上任意一点,则PC≥PQ
A
B
C
P
Q
【问题2】某种杂志原以每本2.5元的价格销售,可以售出
8万本.根据市场调查,若单价每提高0.1元,销售量就可
能相应减少2 000本,若把提价后杂志的定价设为x元,怎
样用不等式表示销售的总收入仍不低于20万元?
1.某工厂在招标会上,购得甲材料x t,乙材料y t,若维持工厂正常生产,甲、乙两种材料总量至少需要120 t,则x、y应满足的不等关系是( )
A.x+y>120
B.x+y<120
C.x+y≥120
D.x+y≤120
C
[解析] 由题意可得x+y≥120,故选C.
练一练
2. 比较两个实数的大小
【问题3】
由于数轴上的点与实数一一对应,所以可以利用数轴上的点的位置关系来
规定实数的大小关系;如图,设是两个实数,他们在数轴上所对应的点分
别是A,B,当点A在点B的左边时,;当点A在点B的右边时,;当
点A和点B重合时,.
A
B
B
A
A(B)
实数大小比较
的基本事实
【作差法】
①
②
③
例1:比较和的大小.
【解】运用作差法:
2>0,
>
作差
变形
定号
定论
0是相等与不等的分界线,它也为比较实数的大小提供了标杆.
典例1
【解】运用作差法:
练一练
3.已知x<y<0,比较(x2+y2)(x-y)与
(x2-y2)(x+y)的大小.
[解析] ∵x<y<0,xy>0,x-y<0,
∴(x2+y2)(x-y)-(x2-y2)(x+y)=-2xy(x-y)>0,
∴(x2+y2)(x-y)>(x2-y2)(x+y).
练一练
3. 重要不等式
若设直角三角形的两直角边分别为a,b,则
S大于S',即
A
B
C
D
E(FGH)
当a=b时,S=S',即
A
B
C
D
E
F
G
H
a
b
当a=b时
综上,
(1)正方形ABCD的面积S=________;
四个直角三角形的面积和S' =_____;
(2) S与S’有什么样的不等关系,如何表示?
(3)S与S’会出现相等的情况吗,什么时候相等?
【问题4】
【问题5】 :如何证明重要不等式?
证明:
重要不等式
【证】:
典例1
4.设M=x2,N=-x-1,则M与N的大小关系是 ( )
A.M>N B.M=N
C.M
练一练
[解析] 2. x2+y2+1-2(x+y-1)
=x2-2x+1+y2-2y+2
=(x-1)2+(y-1)2+1>0,
∴x2+y2+1>2(x+y-1).
5.比较x2+y2+1与2(x+y-1)的大小;
练一练
课堂练习
1.完成一项装修工程,请木工需付工资每人500元,请瓦工需付工资每人400元,现有工人工资预算20 000元,设木工x(x≥0)人,瓦工y(y≥0)人,则关于工资x,y满足的不等关系是( )
A.5x+4y<200 B.5x+4y≥200
C.5x+4y=200 D.5x+4y≤200
D
A
3.已知甲、乙两种食物的维生素A,B含量如下表:
设用x kg的甲种食物与y kg的乙种食物配成混合食物,并使混合食物内至少含有56 000单位的维生素A和63 000 单位的维生素B.试用不等式组表示x,y所满足的不等关系.
4.将一个三边长度分别为5,12,13的三角形的各边都缩短x,构成一个钝角三角形,试用不等式(组)表示x应满足的不等关系.
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
