1.1.1空间向量及其线性运算 课件(共18张PPT)
文档属性
| 名称 | 1.1.1空间向量及其线性运算 课件(共18张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-19 11:42:57 | ||
图片预览





文档简介
(共18张PPT)
第一章 空间向量与立体几何
1.1.1空间向量及其线性运算
1、定义:
有大小又有方向的量。
几何表示法:用有向线段表示
字母表示法:用小写字母表示,或用
表示向量起点和终点字母表示。
3、相等向量:长度相等且方向相同的向量
A
B
C
D
2、表示法:
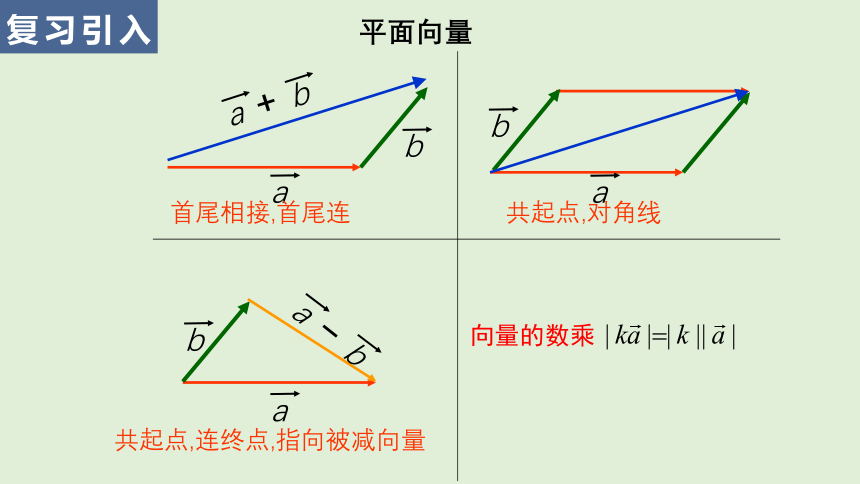
复习引入
平面向量
a
b
b
a
a
b
a -
b
a +
b
向量的数乘
首尾相接,首尾连
共起点,对角线
共起点,连终点,指向被减向量
复习引入
平面向量
加法交换律:
加法结合律:
数乘分配律:
平面向量
复习引入
通过预习你发现空间向量和平面向量有什么区别?
空间向量与平面向量没有本质区别
课堂探究
1、空间向量的概念
空间中既有大小又有方向的量
2、空间向量的表示方法。
O
A
3、什么样的向量是相等的?
记作: 或
OA
a
相等向量:长度相等且方向相同的向量
A
B
C
D
课堂探究
b
a
O
A
B
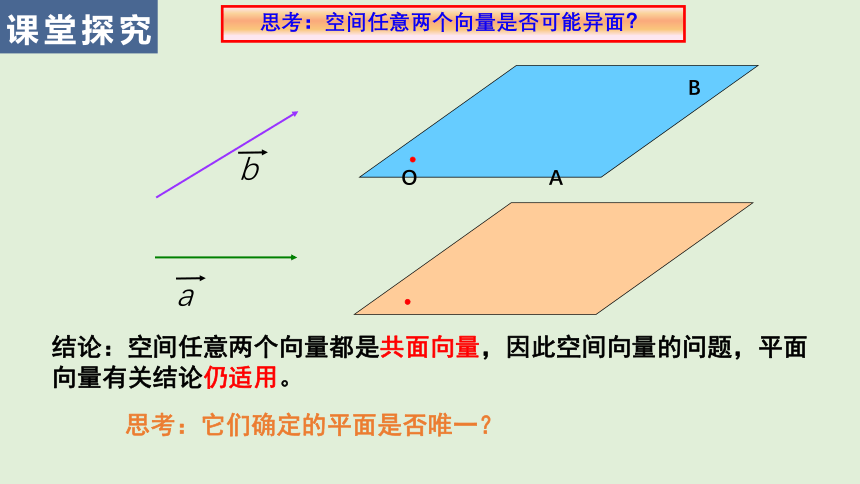
结论:空间任意两个向量都是共面向量,因此空间向量的问题,平面
向量有关结论仍适用。
思考:它们确定的平面是否唯一?
思考:空间任意两个向量是否可能异面?
课堂探究
1.共面向量:平行于同一平面的向量,叫做共面向量.
O
A
注意:空间任意两个向量是共面的,但空间任意三个向量就不一定共面的了。
课堂探究
平行或重合
课堂探究
方向向量
课堂探究
例1:已知平行六面体ABCD-A1B1C1D1,化简下列向量表达式,并标出化简结果的向量.(如图)
A
B
C
D
A1
B1
C1
D1
G
M
始点相同的三个不共面向量之和,等于以这三个向量
为棱的平行六面体的以公共始点为始点的对角线所示向量
例题解析
例2 已知 ABCD ,从平面AC外一点O引向量
求证:四点E、F、G、H共面;
证明:
∵四边形ABCD为
∴
所以 E、F、G、H共面。
例题解析
例题解析
例题解析
练习巩固
练习巩固
你学到了什么?
课堂小结
作业1:书本P5 P9
作业2:预习下一节
作业布置
第一章 空间向量与立体几何
1.1.1空间向量及其线性运算
1、定义:
有大小又有方向的量。
几何表示法:用有向线段表示
字母表示法:用小写字母表示,或用
表示向量起点和终点字母表示。
3、相等向量:长度相等且方向相同的向量
A
B
C
D
2、表示法:
复习引入
平面向量
a
b
b
a
a
b
a -
b
a +
b
向量的数乘
首尾相接,首尾连
共起点,对角线
共起点,连终点,指向被减向量
复习引入
平面向量
加法交换律:
加法结合律:
数乘分配律:
平面向量
复习引入
通过预习你发现空间向量和平面向量有什么区别?
空间向量与平面向量没有本质区别
课堂探究
1、空间向量的概念
空间中既有大小又有方向的量
2、空间向量的表示方法。
O
A
3、什么样的向量是相等的?
记作: 或
OA
a
相等向量:长度相等且方向相同的向量
A
B
C
D
课堂探究
b
a
O
A
B
结论:空间任意两个向量都是共面向量,因此空间向量的问题,平面
向量有关结论仍适用。
思考:它们确定的平面是否唯一?
思考:空间任意两个向量是否可能异面?
课堂探究
1.共面向量:平行于同一平面的向量,叫做共面向量.
O
A
注意:空间任意两个向量是共面的,但空间任意三个向量就不一定共面的了。
课堂探究
平行或重合
课堂探究
方向向量
课堂探究
例1:已知平行六面体ABCD-A1B1C1D1,化简下列向量表达式,并标出化简结果的向量.(如图)
A
B
C
D
A1
B1
C1
D1
G
M
始点相同的三个不共面向量之和,等于以这三个向量
为棱的平行六面体的以公共始点为始点的对角线所示向量
例题解析
例2 已知 ABCD ,从平面AC外一点O引向量
求证:四点E、F、G、H共面;
证明:
∵四边形ABCD为
∴
所以 E、F、G、H共面。
例题解析
例题解析
例题解析
练习巩固
练习巩固
你学到了什么?
课堂小结
作业1:书本P5 P9
作业2:预习下一节
作业布置
