冀教版数学七年级上册 2.3 线段的长短 课件(共13张PPT)
文档属性
| 名称 | 冀教版数学七年级上册 2.3 线段的长短 课件(共13张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 3.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-19 22:08:32 | ||
图片预览



文档简介
(共14张PPT)
2.3 线段的长短
第二章几何图形的初步认识
学习目标
1.掌握线段长短比较的正确方法及表示方法;(重点)
2.学会用尺规作一条线段等于已知线段;(重点)
3.了解“两点之间的所有连线中,线段最短”的基本事实.(重点)
导入新课
有一根长木棒,如何从它上面截下一段,使截下的木棒等于另一根短木棒的长?
还有其他方法吗?
情境引入
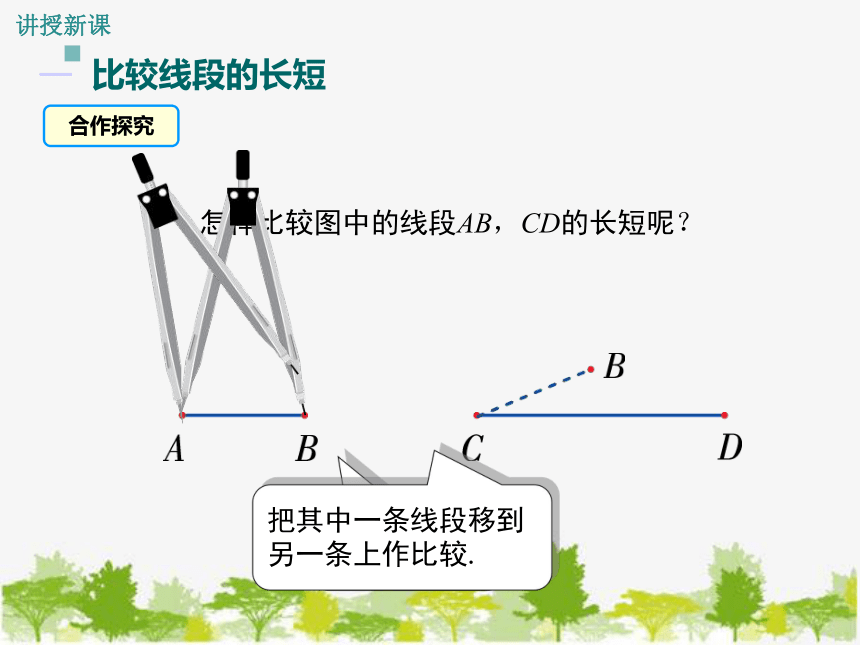
怎样比较图中的线段AB,CD的长短呢?
用刻度尺测量的办法.
把其中一条线段移到另一条上作比较.
讲授新课
比较线段的长短
一
合作探究
C
D
(A)
B
<
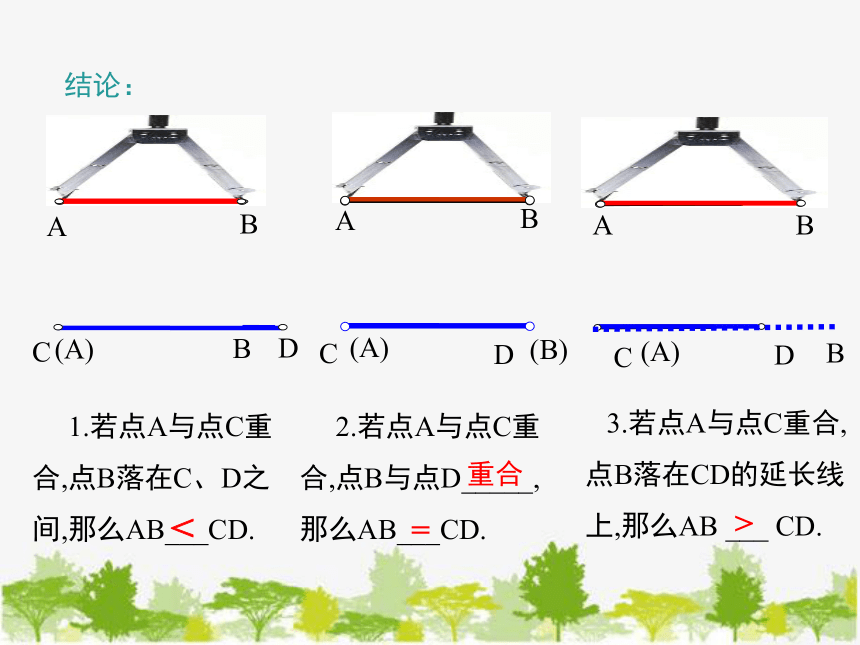
结论:
B
A
C
(B)
(A)
D
A
B
C
D
B
(A)
B
A
1.若点A与点C重合,点B落在C、D之间,那么AB___CD.
2.若点A与点C重合,点B与点D_____,那么AB___CD.
3.若点A与点C重合,点B落在CD的延长线上,那么AB ___ CD.
重合
>
=
作一条线段等于已知线段
已知:线段a, 作一条线段AB,使AB=a.
第一步:画射线AF;
第二步:以A为圆心,a为半径画弧,交射线AF于点B;
∴线段AB为所求.
a
A F
a
B
尺规作图:
基本作图(1):
作一线段等于已知线段.
合作探究
试比较线段AB、CD的长短.
(1) 度量法
(2) 叠合法
将一线段“移动”,使其一端点与另一线段的一端点重合,两线段的另一端点均在同一射线上.
A
D
B
a
b
F
A B
C D
a
b
练一练
C
CD>AB
基本事实及两点间的距离
二
杭州湾跨海大桥是跨越杭州湾的便捷通道. 大桥北起嘉兴市,跨越宽阔的杭州湾海域后止于宁波市,全长36km. 大桥建成后宁波至上海间的陆路距离缩短了约120km. 你知道这是根据什么原理吗?
议一议
两点之间的所有连线中,线段最短
简单说成:两点之间线段最短.
结论
两点之间线段的长度,叫做
两点之间的距离.
[解析] 在MN上任选一点P,它到A,B的距离即线段PA与PB的长,结合两点之间线段最短可求.
例 如图所示,直线MN表示一条铁路,铁路两旁各有一点A和B,表示两个工厂.要在铁路上建一货站,使它到两厂距离之和最短,这个货站应建在何处?
解:连接AB,交MN于点P,则这个货站应建在点P处
P
P
典例精析
(1)两点之间的距离的概念描述的是数量,而不是图形,指的是连接两点的线段的长度,而不是线段本身.
(2)在解决选择位置、求最短距离等问题时,通常转化为“两点之间线段最短”.
[归纳总结]
当堂练习
1.用圆规截取的方法比较图中下列两组线段的大小:
(1) AC 和AB; (2) BC 和AB.
(1) AC < AB
(2) BC < AB
2.如图,AB+BC AC,AC+BC AB,
AB+AC BC(填“>”“<”或“=”).
其中蕴含的数学道理是 .
C
B
>
>
>
两点之间线段最短
课堂小结
线段的长短
线段的长短比较
度量法
叠合法
尺规作图
两点之间线段最短
2.3 线段的长短
第二章几何图形的初步认识
学习目标
1.掌握线段长短比较的正确方法及表示方法;(重点)
2.学会用尺规作一条线段等于已知线段;(重点)
3.了解“两点之间的所有连线中,线段最短”的基本事实.(重点)
导入新课
有一根长木棒,如何从它上面截下一段,使截下的木棒等于另一根短木棒的长?
还有其他方法吗?
情境引入
怎样比较图中的线段AB,CD的长短呢?
用刻度尺测量的办法.
把其中一条线段移到另一条上作比较.
讲授新课
比较线段的长短
一
合作探究
C
D
(A)
B
<
结论:
B
A
C
(B)
(A)
D
A
B
C
D
B
(A)
B
A
1.若点A与点C重合,点B落在C、D之间,那么AB___CD.
2.若点A与点C重合,点B与点D_____,那么AB___CD.
3.若点A与点C重合,点B落在CD的延长线上,那么AB ___ CD.
重合
>
=
作一条线段等于已知线段
已知:线段a, 作一条线段AB,使AB=a.
第一步:画射线AF;
第二步:以A为圆心,a为半径画弧,交射线AF于点B;
∴线段AB为所求.
a
A F
a
B
尺规作图:
基本作图(1):
作一线段等于已知线段.
合作探究
试比较线段AB、CD的长短.
(1) 度量法
(2) 叠合法
将一线段“移动”,使其一端点与另一线段的一端点重合,两线段的另一端点均在同一射线上.
A
D
B
a
b
F
A B
C D
a
b
练一练
C
CD>AB
基本事实及两点间的距离
二
杭州湾跨海大桥是跨越杭州湾的便捷通道. 大桥北起嘉兴市,跨越宽阔的杭州湾海域后止于宁波市,全长36km. 大桥建成后宁波至上海间的陆路距离缩短了约120km. 你知道这是根据什么原理吗?
议一议
两点之间的所有连线中,线段最短
简单说成:两点之间线段最短.
结论
两点之间线段的长度,叫做
两点之间的距离.
[解析] 在MN上任选一点P,它到A,B的距离即线段PA与PB的长,结合两点之间线段最短可求.
例 如图所示,直线MN表示一条铁路,铁路两旁各有一点A和B,表示两个工厂.要在铁路上建一货站,使它到两厂距离之和最短,这个货站应建在何处?
解:连接AB,交MN于点P,则这个货站应建在点P处
P
P
典例精析
(1)两点之间的距离的概念描述的是数量,而不是图形,指的是连接两点的线段的长度,而不是线段本身.
(2)在解决选择位置、求最短距离等问题时,通常转化为“两点之间线段最短”.
[归纳总结]
当堂练习
1.用圆规截取的方法比较图中下列两组线段的大小:
(1) AC 和AB; (2) BC 和AB.
(1) AC < AB
(2) BC < AB
2.如图,AB+BC AC,AC+BC AB,
AB+AC BC(填“>”“<”或“=”).
其中蕴含的数学道理是 .
C
B
>
>
>
两点之间线段最短
课堂小结
线段的长短
线段的长短比较
度量法
叠合法
尺规作图
两点之间线段最短
同课章节目录
- 第一章 有理数
- 1.1 正数和负数
- 1.2 数轴
- 1.3 绝对值与相反数
- 1.4 有理数的大小
- 1.5 有理数的加法
- 1.6 有理数的减法
- 1.7 有理数的加减混合运算
- 1.8 有理数的乘法
- 1.9 有理数的除法
- 1.10 有理数的乘方
- 1.11 有理数的混合运算
- 1.12 计算器的使用
- 第二章 几何图形的初步认识
- 2.1 从生活中认识几何图形
- 2.2 点和线
- 2.3 线段长短的比较
- 2.4 线段的和与差
- 2.5 角以及角的度量
- 2.6 角的大小
- 2.7 角的和与差
- 2.8 平面图形的旋转
- 第三章 代数式
- 3.1 用字母表示数
- 3.2 代数式
- 3.3 代数式的值
- 第四章 整式的加减
- 4.1 整式
- 4.2 合并同类项
- 4.3 去括号
- 4.4 整式的加减
- 第五章 一元一次方程
- 5.1一元一次方程
- 5.2 等式的基本性质
- 5.3 解一元一次方程
- 5.4 一元一次方程的应用
