13.3.2含30°角的直角三角形的性质 课件(共28张PPT)
文档属性
| 名称 | 13.3.2含30°角的直角三角形的性质 课件(共28张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-22 16:12:55 | ||
图片预览







文档简介
(共28张PPT)
13.3.2 含30°角的直角三角形的性质
人教版八年级上册
知识回顾
1.等边三角形的性质有哪些?
2.等边三角形的判断有哪些?
①三边相等的三角形是等边三角形;
②三个角都相等的三角形是等边三角形;
③有一个角是60°的等腰三角形是等边三角形.
①等边三角形的三条边都相等;
②等边三角形的三个角都相等,且每个角都是60°;
③等边三角形每条边上的高、中线和每个角的平分线都重合,有3条对称轴
教学目标
1.探索含30°角的直角三角形的性质.
2.会运用含30°角的直角三角形的性质进行有关的证明和计算.
新知导入
含30°角的直角三角形的性质
知识点 1
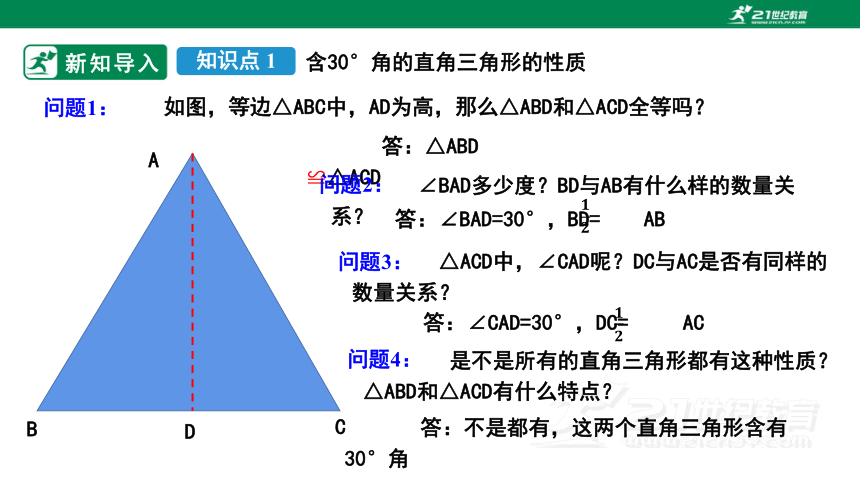
如图,等边△ABC中,AD为高,那么△ABD和△ACD全等吗?
A
问题1:
B
C
D
答:△ABD ≌△ACD
问题2:
∠BAD多少度?BD与AB有什么样的数量关系?
问题3:
△ACD中,∠CAD呢?DC与AC是否有同样的数量关系?
是不是所有的直角三角形都有这种性质? △ABD和△ACD有什么特点?
问题4:
答:不是都有,这两个直角三角形含有30°角
答:∠CAD=30°,DC= AC
答:∠BAD=30°,BD= AB
新知探究
A
B
D
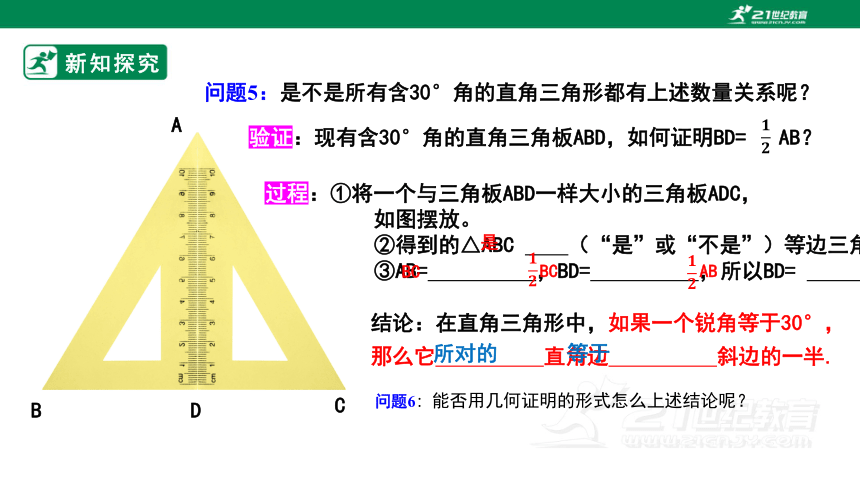
问题5:是不是所有含30°角的直角三角形都有上述数量关系呢?
过程:①将一个与三角板ABD一样大小的三角板ADC,
如图摆放。
②得到的△ABC (“是”或“不是”)等边三角形
③AB= ,BD= ,所以BD=
是
C
BC
问题6:能否用几何证明的形式怎么上述结论呢?
结论:在直角三角形中,如果一个锐角等于30°,
那么它 直角边 斜边的一半.
所对的
等于
BC
AB
验证:现有含30°角的直角三角板ABD,如何证明BD= AB?
新知探究
证明:延长BC 到D,使BD =AB,连接AD.
在△ABC 中,
∵ ∠C =90°,∠A =30°,
∴ ∠B =60°.
∴△ABD 是等边三角形.
又∵AC⊥BD,
已知:如图,在Rt△ABC 中,∠C =90°,∠A =30°.
求证:BC = AB.
A
B
C
D
∴BC = AB.
∴BC = BD.
分析:参考刚才三角板的方法,可以先延长 ,使 ,连接 ,这样情况就和三角板时候一模一样了。
BC 到D
BD =AB
AD
新知探究
如图,在Rt△ABC中,∠ACB=90°,∠A=30°.
求证:BC= AB.
证明:在斜边AB上截取BD=BC,连接CD.
A
C
B
D
证法2
∵在Rt△ABC中,∠A=30°, ∴∠B=60°.
∵BD=BC,∠B=60° ,
∴△BCD为等边三角形,
∴∠DCB=60°,CD=BC=BD.∴∠ACD=∠A=30°,
∴AD=CD. ∴BC=CD=BD=AD.
∴BC= AB.
新知小结
含30°角的直角三角形的性质:在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半.
几何语言:如图,在Rt△ABC中,∠C=90°,
∵∠A=30°,
∴BC= AB.
A
C
B
含30°角的直角三角形的性质
新知典例
例1 如图,在△ABC中,已知∠ACB=90°,CD垂直于AB,垂足为点D,∠A=30°,BD=3,则AB= .
解:∵∠ACB=90°,∠A=30°,
∴∠B=90°﹣∠A=60°,
∵CD⊥AB,
∴∠CDB=90°,
∴∠DCB=90°﹣∠B=30°,
∴BC=2BD=6,
∴AB=2BC=12,
12
课堂练习
1.如图所示,在△ABC中,∠C=90°,∠A=30°,DE为AB的中垂线,AD=12,则CD的长是( )
A.3 B.4 C.6 D.8
解:∵∠A=30°,AD=12,DE垂直平分AB,
∴DE=6,DA=DB,
∴∠DBE=∠A=30°,
∵Rt△ABC中,∠C=90°,
∴∠CBA=60°,
∴∠DBE=∠DBC=30°,
∴BD平分∠CBE,
∵∠C=90°,DE⊥AB,
∴CD=DE=6,
C
课堂小结
方法总结:含30°角的直角三角形的性质是表示线段倍分关系的一个重要的依据,如果问题中出现探究线段倍分关系的结论时,要联想此性质.
新知探究
问题7: 这个性质的逆命题还成立吗?请试着证明你的猜想.
含30°角的直角三角形的性质:
.
在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半
逆命题:
.
在直角三角形中,如果一条直角边等于斜边的一半,那么这条直角边所对的角等于30°
已知:如图
A
C
B
求证:
∠A=30°.
Rt△ABC中,∠C=90°,BC= AB.
含30°角的直角三角形的判定
知识点 2
新知探究
已知:如图
A
C
B
求证:
∠A=30°.
Rt△ABC中,∠C=90°,BC= AB.
D
证明:延长BC 到D,使CD =BC,连接AD.
∵ ∠C =90°,
∴ AC⊥BD,
∴AC垂直平分BD,
∴AD=AB,
∴BD=AB=AD,
∴∠B =60°,
∴∠CAB =30°.
∵BC=CD= AB,
逆命题成立
课堂小结
直角三角形中的一条直角边等于斜边的一半,那么这条直角边所对的角等于30°.
含30°角的直角三角形的判定
几何语言:
如图,在Rt△ABC中,∠C=90°
A
C
B
∵BC= AB,
∴∠A=30°.
新知典例
例2 已知:在等腰△ABC中,AD⊥BC,垂足为点D,AD= ,则∠C的度数有几种可能( )
A.6种 B.5种 C.4种 D.3种
BC
解:(1)当∠C为底角时,
①如图1,当AB=AC时,
∵AD⊥BC,
∴BD=CD,
∵AD=
∴AD=BD=CD,
∴∠C=45°;
BC,
②如图2,当AB=BC时,
∵AD=
∴AD=
∴∠ABD=30°,
∴∠C=75°;
BC,
AB,
B
新知典例
例2.已知:在等腰△ABC中,AD⊥BC,垂足为点D,AD= ,则∠C的度数有几种可能( )
A.6种 B.5种 C.4种 D.3种
BC
③如图3,当AB=BC时,
∵AD= ,AB=BC,
∴AD= ,
∴∠DBA=30°,
∴∠C=15°;
BC
AB,
(2)当∠C为顶角时,
①如图4,AC=BC,
∵AD⊥BC,
∴∠ADC=90°,
∵AD= ,
∴AD= ,
∴∠C=30°;
BC
AC
B
②如图5,AC=BC,
∵AD⊥BC,
∴∠ADC=90°,
∵AD= ,
∴AD= ,
∴∠ACD=30°,
∴∠ACB=150°.
BC
AC
综上所述,∠ACB的度数为45°或75°或15°或30°或150°.
课堂练习
2.若等腰三角形腰上的高是腰长的一半,则这个等腰三角形的底角是( )
A.75°或30° B.75° C.15° D.75°和15°
解:当等腰三角形是锐角三角形时,如图1所示,
∵AD⊥AC,AD=
∴∠B=30°,
∴∠C=∠BAC=75°;
AB
当等腰三角形是钝角三角形时,如图2所示,
∵CD⊥AB,即在直角三角形ACD中,CD=
∴∠CAD=30°,
∴∠CAB=150°,
∴∠B=∠ACB=15°.
AC
D
课堂小结
方法总结:利用含30°角的直角三角形的判定解决问题时,注意确定边所对的角,不要看错位置;在处理一些问题时候要考虑多种不同的情况,按照边、角的位置进行分类。
新知探究
利用直角三角形的性质解决实际问题
知识点 3
例3 如图是屋架设计图的一部分,点D 是斜梁AB 的中点,立柱BC、DE 垂直于横梁AC,AB =7.4 cm,∠A =30°,立柱BC、DE 要多长.
A
B
C
D
E
解:∵ DE⊥AC,BC⊥AC,∠A =30°,
∴ BC = AB,DE = AD.
又 AD = AB,
∴ DE = AD =1.85(m) .
∴ BC =3.7(m).
课堂练习
3.如图所示,为了躲避海盗,一轮船由西向东航行,早上8点,在A处测得小岛P在北偏东75°的方向上,以每小时20海里的速度继续向东航行,10点到达B处,并测得小岛P在北偏东60°的方向上,已知小岛周围22海里内有暗礁,若轮船仍向前航行,有无触礁的危险?
解:作PC⊥AB于点C.
∵∠PAB=90°﹣75°=15°,∠PBC=90°﹣60°=30°,
又∵∠PBC=∠PAB+∠APB,
∴∠PAB=∠APB=15°,
∴BP=AB=20×2=40(海里),
在直角△PBC中,PC=
PB=40× =20<22.
则若轮船仍向前航行有触礁的危险.
课堂小结
方法总结:在求三角形边长的一些问题中,可以构造含30°角的直角三角形来解决.本题的关键是作高,而后利用等腰三角形及外角的性质,得出30°角,利用含30°角的直角三角形的性质解决问题.
课堂小测
1.如图,在Rt△ABC中,∠C=90°,∠B=30°,AC=4,则AB的长是( )
A.8 B.1 C.2 D.4
2.如图,在△ABC中,AB=AC,∠C=30°,点D在BC上,AB⊥AD,AD=3cm,则BC的长为 cm.
9
A
课堂小测
3.如图,是柳州市鱼马公园一段索道的示意图,已知A、B两点间的距离为30米,∠A=30°,则缆车从A点到达B点过程中,上升的高度(BC的长)为
米.
15
课堂小测
4.如图,一条船上午8时从海岛A出发,以15海里/时的速度向正北方向航行,上午10时到达海岛B处,分别从A,B处望灯塔C,测得∠NAC=30°,∠NBC=60°.
(1)求海岛B到灯塔C的距离;
(2)若这条船继续向正北航行,问什么时间小船与灯塔C的距离最短?
解:(1)由题意得:
AB=15×2=30(海里).
∵∠NBC=60°,∠NAC=30°,
∴∠ACB=∠NBC﹣∠NAC=30°.
∴∠ACB=∠NAC.
∴AB=BC=30 (海里).
∴从海岛B到灯塔C的距离为30海里.
(2)如图,过点C作CP⊥AB于点P.
∴根据垂线段最短,线段CP的长为小船与灯塔C的最短距离,∠BPC=90°.
又∵∠NBC=60°,
∴∠PCB=180°﹣∠BPC﹣∠CBP=30°.
在Rt△CBP中,∠BCP=30°,
∴ (海里),
∴AP=AB+BP=30+15=45(海里).
∴航行的时间为45÷15=3(时).
∴若这条船继续向正北航行,上午11时小船与灯塔C的距离最短.
课堂小测
5.如图,在△ABC中,∠ACB=90°,∠A=30°,AB的垂直平分线分别交AB和AC于点D、E,CE=6,求AC的长.
解:连接BE,
∵DE为AB边的垂直平分线,
∴BE=AE,
∵∠A=30°,∠ACB=90°,
∴∠ABC=60°
∴∠EBA=∠A=30°,
在Rt△BCE中,∠EBC=∠ABC﹣∠EBA=30°,
∴BE=2EC=12,
∴AC=AE+EC=BE+EC=12+6=18.
课堂总结
含30°角的直角三角形
性质
判定(拓展)
在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半.
直角三角形中,如果一条直角边等于斜边的一半,那么它所对的角等于30°.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
13.3.2 含30°角的直角三角形的性质
人教版八年级上册
知识回顾
1.等边三角形的性质有哪些?
2.等边三角形的判断有哪些?
①三边相等的三角形是等边三角形;
②三个角都相等的三角形是等边三角形;
③有一个角是60°的等腰三角形是等边三角形.
①等边三角形的三条边都相等;
②等边三角形的三个角都相等,且每个角都是60°;
③等边三角形每条边上的高、中线和每个角的平分线都重合,有3条对称轴
教学目标
1.探索含30°角的直角三角形的性质.
2.会运用含30°角的直角三角形的性质进行有关的证明和计算.
新知导入
含30°角的直角三角形的性质
知识点 1
如图,等边△ABC中,AD为高,那么△ABD和△ACD全等吗?
A
问题1:
B
C
D
答:△ABD ≌△ACD
问题2:
∠BAD多少度?BD与AB有什么样的数量关系?
问题3:
△ACD中,∠CAD呢?DC与AC是否有同样的数量关系?
是不是所有的直角三角形都有这种性质? △ABD和△ACD有什么特点?
问题4:
答:不是都有,这两个直角三角形含有30°角
答:∠CAD=30°,DC= AC
答:∠BAD=30°,BD= AB
新知探究
A
B
D
问题5:是不是所有含30°角的直角三角形都有上述数量关系呢?
过程:①将一个与三角板ABD一样大小的三角板ADC,
如图摆放。
②得到的△ABC (“是”或“不是”)等边三角形
③AB= ,BD= ,所以BD=
是
C
BC
问题6:能否用几何证明的形式怎么上述结论呢?
结论:在直角三角形中,如果一个锐角等于30°,
那么它 直角边 斜边的一半.
所对的
等于
BC
AB
验证:现有含30°角的直角三角板ABD,如何证明BD= AB?
新知探究
证明:延长BC 到D,使BD =AB,连接AD.
在△ABC 中,
∵ ∠C =90°,∠A =30°,
∴ ∠B =60°.
∴△ABD 是等边三角形.
又∵AC⊥BD,
已知:如图,在Rt△ABC 中,∠C =90°,∠A =30°.
求证:BC = AB.
A
B
C
D
∴BC = AB.
∴BC = BD.
分析:参考刚才三角板的方法,可以先延长 ,使 ,连接 ,这样情况就和三角板时候一模一样了。
BC 到D
BD =AB
AD
新知探究
如图,在Rt△ABC中,∠ACB=90°,∠A=30°.
求证:BC= AB.
证明:在斜边AB上截取BD=BC,连接CD.
A
C
B
D
证法2
∵在Rt△ABC中,∠A=30°, ∴∠B=60°.
∵BD=BC,∠B=60° ,
∴△BCD为等边三角形,
∴∠DCB=60°,CD=BC=BD.∴∠ACD=∠A=30°,
∴AD=CD. ∴BC=CD=BD=AD.
∴BC= AB.
新知小结
含30°角的直角三角形的性质:在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半.
几何语言:如图,在Rt△ABC中,∠C=90°,
∵∠A=30°,
∴BC= AB.
A
C
B
含30°角的直角三角形的性质
新知典例
例1 如图,在△ABC中,已知∠ACB=90°,CD垂直于AB,垂足为点D,∠A=30°,BD=3,则AB= .
解:∵∠ACB=90°,∠A=30°,
∴∠B=90°﹣∠A=60°,
∵CD⊥AB,
∴∠CDB=90°,
∴∠DCB=90°﹣∠B=30°,
∴BC=2BD=6,
∴AB=2BC=12,
12
课堂练习
1.如图所示,在△ABC中,∠C=90°,∠A=30°,DE为AB的中垂线,AD=12,则CD的长是( )
A.3 B.4 C.6 D.8
解:∵∠A=30°,AD=12,DE垂直平分AB,
∴DE=6,DA=DB,
∴∠DBE=∠A=30°,
∵Rt△ABC中,∠C=90°,
∴∠CBA=60°,
∴∠DBE=∠DBC=30°,
∴BD平分∠CBE,
∵∠C=90°,DE⊥AB,
∴CD=DE=6,
C
课堂小结
方法总结:含30°角的直角三角形的性质是表示线段倍分关系的一个重要的依据,如果问题中出现探究线段倍分关系的结论时,要联想此性质.
新知探究
问题7: 这个性质的逆命题还成立吗?请试着证明你的猜想.
含30°角的直角三角形的性质:
.
在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半
逆命题:
.
在直角三角形中,如果一条直角边等于斜边的一半,那么这条直角边所对的角等于30°
已知:如图
A
C
B
求证:
∠A=30°.
Rt△ABC中,∠C=90°,BC= AB.
含30°角的直角三角形的判定
知识点 2
新知探究
已知:如图
A
C
B
求证:
∠A=30°.
Rt△ABC中,∠C=90°,BC= AB.
D
证明:延长BC 到D,使CD =BC,连接AD.
∵ ∠C =90°,
∴ AC⊥BD,
∴AC垂直平分BD,
∴AD=AB,
∴BD=AB=AD,
∴∠B =60°,
∴∠CAB =30°.
∵BC=CD= AB,
逆命题成立
课堂小结
直角三角形中的一条直角边等于斜边的一半,那么这条直角边所对的角等于30°.
含30°角的直角三角形的判定
几何语言:
如图,在Rt△ABC中,∠C=90°
A
C
B
∵BC= AB,
∴∠A=30°.
新知典例
例2 已知:在等腰△ABC中,AD⊥BC,垂足为点D,AD= ,则∠C的度数有几种可能( )
A.6种 B.5种 C.4种 D.3种
BC
解:(1)当∠C为底角时,
①如图1,当AB=AC时,
∵AD⊥BC,
∴BD=CD,
∵AD=
∴AD=BD=CD,
∴∠C=45°;
BC,
②如图2,当AB=BC时,
∵AD=
∴AD=
∴∠ABD=30°,
∴∠C=75°;
BC,
AB,
B
新知典例
例2.已知:在等腰△ABC中,AD⊥BC,垂足为点D,AD= ,则∠C的度数有几种可能( )
A.6种 B.5种 C.4种 D.3种
BC
③如图3,当AB=BC时,
∵AD= ,AB=BC,
∴AD= ,
∴∠DBA=30°,
∴∠C=15°;
BC
AB,
(2)当∠C为顶角时,
①如图4,AC=BC,
∵AD⊥BC,
∴∠ADC=90°,
∵AD= ,
∴AD= ,
∴∠C=30°;
BC
AC
B
②如图5,AC=BC,
∵AD⊥BC,
∴∠ADC=90°,
∵AD= ,
∴AD= ,
∴∠ACD=30°,
∴∠ACB=150°.
BC
AC
综上所述,∠ACB的度数为45°或75°或15°或30°或150°.
课堂练习
2.若等腰三角形腰上的高是腰长的一半,则这个等腰三角形的底角是( )
A.75°或30° B.75° C.15° D.75°和15°
解:当等腰三角形是锐角三角形时,如图1所示,
∵AD⊥AC,AD=
∴∠B=30°,
∴∠C=∠BAC=75°;
AB
当等腰三角形是钝角三角形时,如图2所示,
∵CD⊥AB,即在直角三角形ACD中,CD=
∴∠CAD=30°,
∴∠CAB=150°,
∴∠B=∠ACB=15°.
AC
D
课堂小结
方法总结:利用含30°角的直角三角形的判定解决问题时,注意确定边所对的角,不要看错位置;在处理一些问题时候要考虑多种不同的情况,按照边、角的位置进行分类。
新知探究
利用直角三角形的性质解决实际问题
知识点 3
例3 如图是屋架设计图的一部分,点D 是斜梁AB 的中点,立柱BC、DE 垂直于横梁AC,AB =7.4 cm,∠A =30°,立柱BC、DE 要多长.
A
B
C
D
E
解:∵ DE⊥AC,BC⊥AC,∠A =30°,
∴ BC = AB,DE = AD.
又 AD = AB,
∴ DE = AD =1.85(m) .
∴ BC =3.7(m).
课堂练习
3.如图所示,为了躲避海盗,一轮船由西向东航行,早上8点,在A处测得小岛P在北偏东75°的方向上,以每小时20海里的速度继续向东航行,10点到达B处,并测得小岛P在北偏东60°的方向上,已知小岛周围22海里内有暗礁,若轮船仍向前航行,有无触礁的危险?
解:作PC⊥AB于点C.
∵∠PAB=90°﹣75°=15°,∠PBC=90°﹣60°=30°,
又∵∠PBC=∠PAB+∠APB,
∴∠PAB=∠APB=15°,
∴BP=AB=20×2=40(海里),
在直角△PBC中,PC=
PB=40× =20<22.
则若轮船仍向前航行有触礁的危险.
课堂小结
方法总结:在求三角形边长的一些问题中,可以构造含30°角的直角三角形来解决.本题的关键是作高,而后利用等腰三角形及外角的性质,得出30°角,利用含30°角的直角三角形的性质解决问题.
课堂小测
1.如图,在Rt△ABC中,∠C=90°,∠B=30°,AC=4,则AB的长是( )
A.8 B.1 C.2 D.4
2.如图,在△ABC中,AB=AC,∠C=30°,点D在BC上,AB⊥AD,AD=3cm,则BC的长为 cm.
9
A
课堂小测
3.如图,是柳州市鱼马公园一段索道的示意图,已知A、B两点间的距离为30米,∠A=30°,则缆车从A点到达B点过程中,上升的高度(BC的长)为
米.
15
课堂小测
4.如图,一条船上午8时从海岛A出发,以15海里/时的速度向正北方向航行,上午10时到达海岛B处,分别从A,B处望灯塔C,测得∠NAC=30°,∠NBC=60°.
(1)求海岛B到灯塔C的距离;
(2)若这条船继续向正北航行,问什么时间小船与灯塔C的距离最短?
解:(1)由题意得:
AB=15×2=30(海里).
∵∠NBC=60°,∠NAC=30°,
∴∠ACB=∠NBC﹣∠NAC=30°.
∴∠ACB=∠NAC.
∴AB=BC=30 (海里).
∴从海岛B到灯塔C的距离为30海里.
(2)如图,过点C作CP⊥AB于点P.
∴根据垂线段最短,线段CP的长为小船与灯塔C的最短距离,∠BPC=90°.
又∵∠NBC=60°,
∴∠PCB=180°﹣∠BPC﹣∠CBP=30°.
在Rt△CBP中,∠BCP=30°,
∴ (海里),
∴AP=AB+BP=30+15=45(海里).
∴航行的时间为45÷15=3(时).
∴若这条船继续向正北航行,上午11时小船与灯塔C的距离最短.
课堂小测
5.如图,在△ABC中,∠ACB=90°,∠A=30°,AB的垂直平分线分别交AB和AC于点D、E,CE=6,求AC的长.
解:连接BE,
∵DE为AB边的垂直平分线,
∴BE=AE,
∵∠A=30°,∠ACB=90°,
∴∠ABC=60°
∴∠EBA=∠A=30°,
在Rt△BCE中,∠EBC=∠ABC﹣∠EBA=30°,
∴BE=2EC=12,
∴AC=AE+EC=BE+EC=12+6=18.
课堂总结
含30°角的直角三角形
性质
判定(拓展)
在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半.
直角三角形中,如果一条直角边等于斜边的一半,那么它所对的角等于30°.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
