【精品解析】沪教版(上海)九下 第二十七章圆与正多边形专项测试练习题(含详解)
文档属性
| 名称 | 【精品解析】沪教版(上海)九下 第二十七章圆与正多边形专项测试练习题(含详解) |

|
|
| 格式 | doc | ||
| 文件大小 | 2.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-19 08:42:08 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
九年级数学第二学期第二十七章圆与正多边形专项测试
考试时间:90分钟;命题人:数学教研组
考生注意:
1、本卷分第I卷(选择题)和第Ⅱ卷(非选择题)两部分,满分100分,考试时间90分钟
2、答卷前,考生务必用0.5毫米黑色签字笔将自己的姓名、班级填写在试卷规定位置上
3、答案必须写在试卷各个题目指定区域内相 ( http: / / www.21cnjy.com )应的位置,如需改动,先划掉原来的答案,然后再写上新的答案;不准使用涂改液、胶带纸、修正带,不按以上要求作答的答案无效。21*cnjy*com
第I卷(选择题 30分)
一、单选题(10小题,每小题3分,共计30分)
1、如图,中,,,,点为的中点,以为圆心,长为半径作半圆,交于点,则图中阴影部分的面积是( )
( http: / / www.21cnjy.com / )
A. B. C. D.
2、如图,AB是⊙O的直径,BD与⊙ ( http: / / www.21cnjy.com )O相切于点B,点C是⊙O上一点,连接AC并延长,交BD于点D,连接OC,BC,若∠BOC=50°,则∠D的度数为( )
( http: / / www.21cnjy.com / )
A.50° B.55° C.65° D.75°
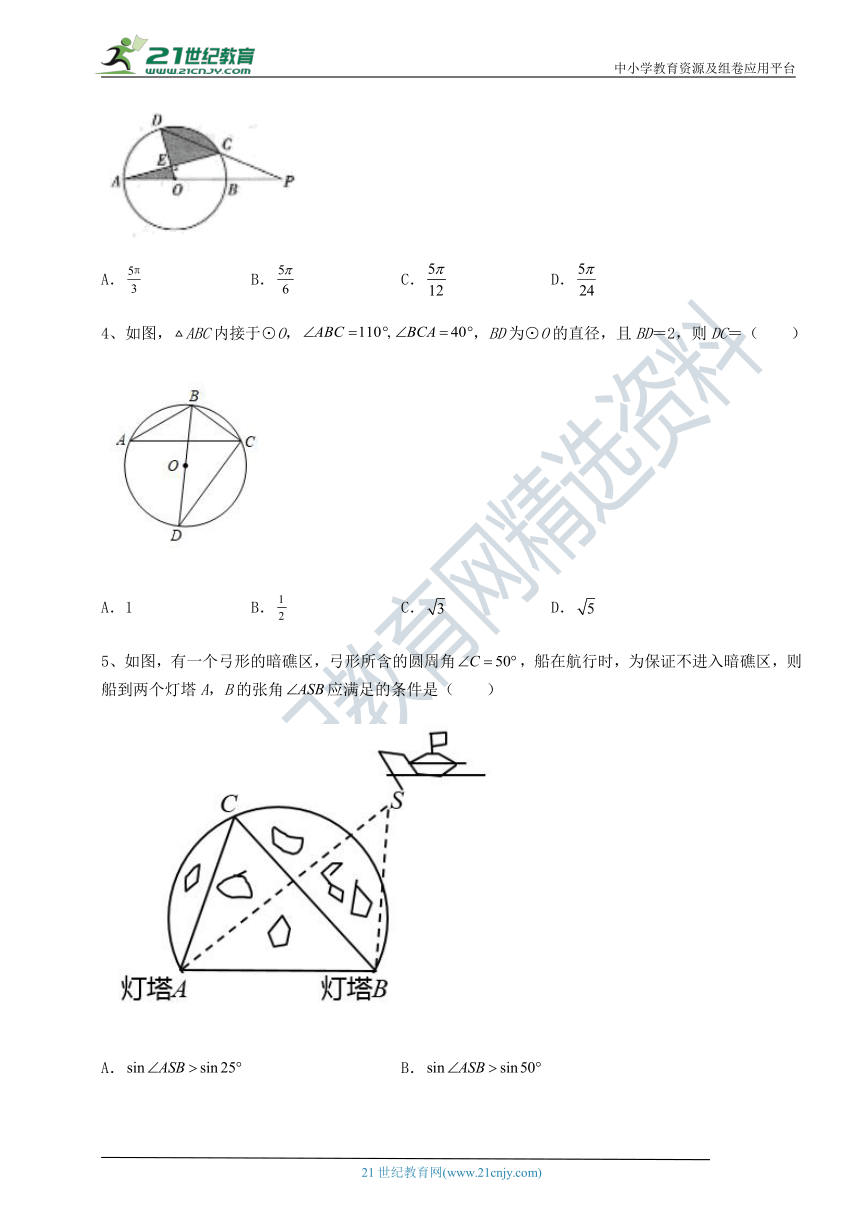
3、如图,AB是的直径,的弦DC的延长线与AB的延长线相交于点P,于点E,,,则阴影部分的面积为( )
( http: / / www.21cnjy.com / )
A. B. C. D.
4、如图,ABC内接于⊙O,,BD为⊙O的直径,且BD=2,则DC=( )
( http: / / www.21cnjy.com / )
A.1 B. C. D.
5、如图,有一个弓形的暗礁区,弓形所含的圆周角,船在航行时,为保证不进入暗礁区,则船到两个灯塔A,B的张角应满足的条件是( )
( http: / / www.21cnjy.com / )
A. B.
C. D.
6、如图,菱形ABCD的顶点B,C,D均在⊙A上,点E在弧BD上,则∠BED的度数为( )
( http: / / www.21cnjy.com / )
A.90° B.120° C.135° D.150°
7、如图,中,,则等于( )
( http: / / www.21cnjy.com / )
A. B. C. D.
8、如图,AB是⊙O的直径,点C是⊙O上一点,若∠BAC=30°,BC=2,则AB的长为( )
( http: / / www.21cnjy.com / )
A.4 B.6 C.8 D.10
9、如图,在中,,,.将绕点按逆时针方向旋转后得到,则图中阴影部分面积为( )
( http: / / www.21cnjy.com / )
A. B. C. D.
10、如图,在中,,,若以点为圆心,的长为半径的圆恰好经过的中点,则的长等于( )
( http: / / www.21cnjy.com / )
A. B. C. D.
第Ⅱ卷(非选择题 70分)
二、填空题(5小题,每小题4分,共计20分)
1、如图,为的直径,弦于点,,,则的长为________.
( http: / / www.21cnjy.com / )
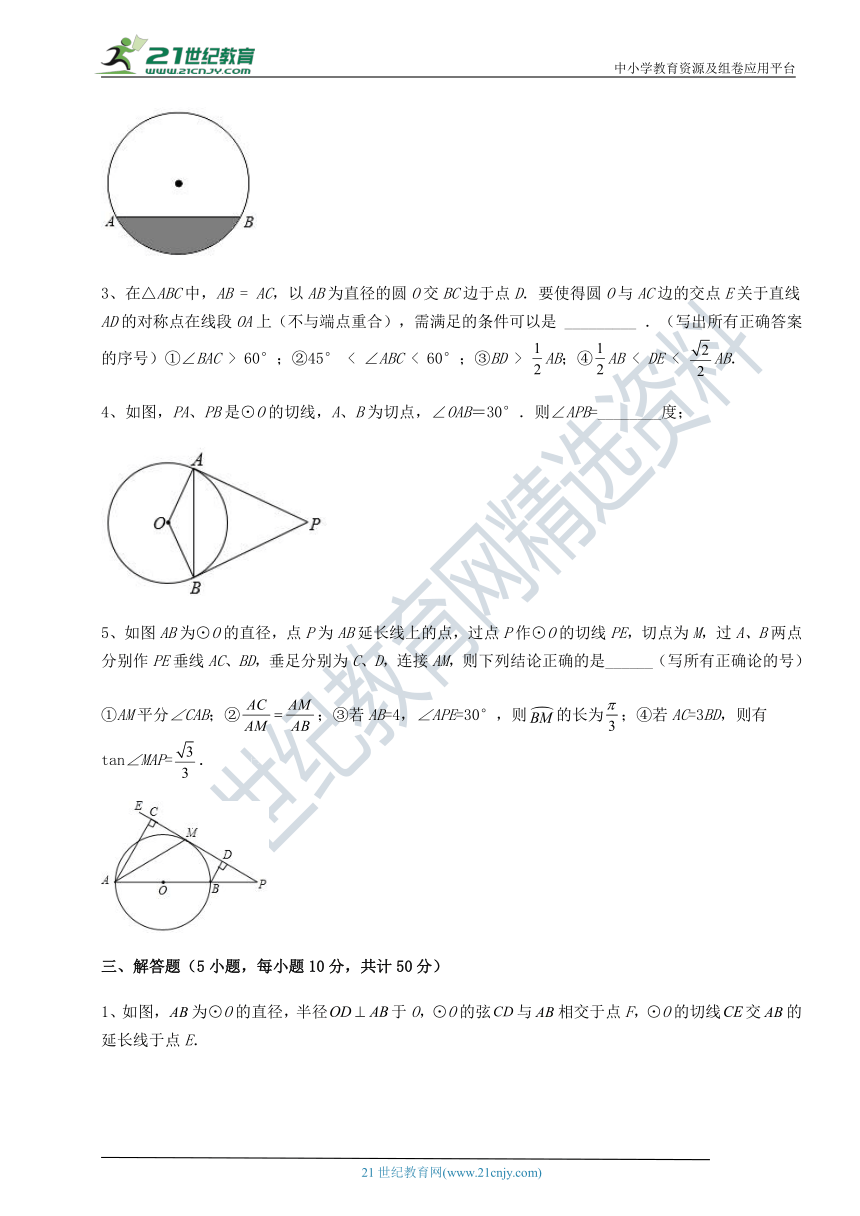
2、往直径为26cm的圆柱形容器内装入一些水以后,截面如图所示,若水的最大深度为8cm,则水面AB的宽度为___cm.
( http: / / www.21cnjy.com / )
3、在△ABC中,AB = AC,以AB为直径的圆O交BC边于点D.要使得圆O与AC边的交点E关于直线AD的对称点在线段OA上(不与端点重合),需满足的条件可以是 _________ .(写出所有正确答案的序号)①∠BAC > 60°;②45° < ∠ABC < 60°;③BD > AB;④AB < DE < AB.
4、如图,PA、PB是⊙O的切线,A、B为切点,∠OAB=30°.则∠APB=________度;
( http: / / www.21cnjy.com / )
5、如图AB为⊙O的直径, ( http: / / www.21cnjy.com )点P为AB延长线上的点,过点P作⊙O的切线PE,切点为M,过A、B两点分别作PE垂线AC、BD,垂足分别为C、D,连接AM,则下列结论正确的是______(写所有正确论的号)
①AM平分∠CAB;②;③若AB=4,∠APE=30°,则的长为;④若AC=3BD,则有tan∠MAP=.2-1-c-n-j-y
( http: / / www.21cnjy.com / )
三、解答题(5小题,每小题10分,共计50分)
1、如图,为⊙O的直径,半径于O,⊙O的弦与相交于点F,⊙O的切线交的延长线于点E.
( http: / / www.21cnjy.com / )
(1)求证:;
(2)若⊙O的半径长为3,且,求的长.
2、在平面直角坐标系xOy中,图 ( http: / / www.21cnjy.com )形W上任意两点间的距离有最大值,将这个最大值记为d.对点P及图形W给出如下定义:点Q为图形W上任意一点,若P,Q两点间的距离有最大值,且最大值恰好为2d,则称点P为图形W的“倍点”.
(1)如图1,图形W是半径为1的⊙O.
①图形W上任意两点间的距离的最大值d为_________;
②在点(0,2) ,(3,3),(,0)中,⊙O的“倍点”是________;
(2)如图2,图形W是中心在原点的正方形ABCD,已知点A(,1),若点E(,3) 是正方形ABCD的“倍点”,求的值;
(3)图形W是长为2的线段MN,T为MN的中点,若在半径为6的⊙O上存在MN的“倍点”,直接写出满足条件的点T所构成的图形的面积.
( http: / / www.21cnjy.com / )
3、如图,点O,B的坐标分别是(0,0),(3,0).将△OAB绕点O逆时针旋转90°,得到△OA1B1.
(1)画出平面直角坐标系和三角形△OA1B1;
(2)求旋转过程中点B走过的路径的长.
( http: / / www.21cnjy.com / )
4、下面是小石设计的“过三角形一个顶点作其对边的平行线”的尺规作图过程.
已知:如图,.
( http: / / www.21cnjy.com / )
求作:直线BD,使得.
作法:如图,
( http: / / www.21cnjy.com / )
①分别作线段AC,BC的垂直平分线,,两直线交于点O;
②以点O为圆心,OA长为半径作圆;
③以点A为圆心,BC长为半径作孤,交于点D;
④作直线BD.所以直线BD就是所求作的直线.
根据小石设计的尺规作图过程,
(1)使用直尺和圆规,补全图形;(保留作图痕迹)
(2)完成下面的证明.
证明:连接AD,
∵点A,B,C,D在上,,
∴______.
∴(______)(填推理的依据).
∴.
5、已知:A,B是直线l上的两点.
求作:ABC,使得点C在直线l上方,且AC=BC,.
作法:①分别以A,B为圆心,AB长为半径画弧,在直线l上方交于点O,在直线l下方交于点E;
②以点O为圆心,OA长为半径画圆;
③作直线OE与直线l上方的⊙O交于点C;
④连接AC,BC.ABC就是所求作的三角形.
(1)使用直尺和圆规,依作法补全图形(保留作图痕迹);
(2)完成下面的证明.
证明:连接OA,OB.
∵OA=OB=AB,
∴OAB是等边三角形.
∴.
∵A,B,C在⊙O上,
∴∠ACB=∠AOB( )(填推理的依据).
∴.
由作图可知直线OE是线段AB的垂直平分线,
∴AC=BC( )(填推理的依据).
∴ABC就是所求作的三角形.
-参考答案-
一、单选题
1、A
【分析】
连接OD,BD,作OH⊥CD交CD于点H,首先根据勾股定理求出BC的长度,然后利用等面积法求出BD的长度,进而得到是等边三角形,,然后根据30°角直角三角形的性质求出OH的长度,最后根据进行计算即可.21cnjy.com
【详解】
解:如图所示,连接OD,BD,作OH⊥CD交CD于点H
( http: / / www.21cnjy.com / )
∵,,
∴在中,
∵点为的中点,以为圆心,长为半径作半圆
∴是圆的直径,
∴
∴,即
解得:
又∵
∴
∴是等边三角形
∴
∴
∵OH⊥CD
∴,
∴.
故选:A.
【点睛】
本题考查了30°角直角三角形的性质,等 ( http: / / www.21cnjy.com )边三角形的性质和判定,扇形面积,勾股定理等知识,正确添加辅助线,熟练掌握和灵活运用相关知识是解题的关键.21·cn·jy·com
2、C
【分析】
首先证明∠ABD=90°,由∠BOC=50°,根据圆周角定理求出∠A的度数即可解决问题.
【详解】
解:∵BD是切线,
∴BD⊥AB,
∴∠ABD=90°,
∵∠BOC=50°,
∴∠A=∠BOC=25°,
∴∠D=90°﹣∠A=65°,
故选:C.
【点睛】
本题考查的是切线的性质、圆周角定理,解题的关键是灵活应用所学知识解决问题,属于中考常考题型.
3、B
【分析】
由垂径定理可知,AE=CE,则阴影部分的面积等于扇形AOD的面积,求出,然后利用扇形面积公式,即可求出答案.21·世纪*教育网
【详解】
解:根据题意,如图:
( http: / / www.21cnjy.com / )
∵AB是的直径,OD是半径,,
∴AE=CE,
∴阴影CED的面积等于AED的面积,
∴,
∵,,
∴,
∴;
故选:B
【点睛】
本题考查了求扇形的面积,垂径定理,解题的关键是掌握所学的知识,正确利用扇形的面积公式进行计算.
4、C
【分析】
根据三角形内角和定理求得,根据同弧所对的圆周角相等可得,根据直径所对的圆周角是直角,含30度角的直角三角形的性质,勾股定理即可求得的长2·1·c·n·j·y
【详解】
解:
为⊙O的直径,
在,, BD=2,
故选C
【点睛】
本题考查了三角形内角和定理,同弧所对的圆周角相等,直径所对的圆周角是直角,勾股定理,含30度角的直角三角形的性质,求得是解题的关键.www-2-1-cnjy-com
5、D
【分析】
本题利用了三角形外角与内角的关系和圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.21*cnjy*com
【详解】
如图,AS交圆于点E,连接EB,
( http: / / www.21cnjy.com / )
由圆周角定理知,∠AEB=∠C=50°,而∠AEB是△SEB的一个外角,由∠AEB>∠S,即当∠S<50°时船不进入暗礁区.【来源:21cnj*y.co*m】
所以,两个灯塔的张角∠ASB应满足的条件是∠ASB<50°.
∴cos∠ASB>cos50°,
故选:D.
【点睛】
本题考查三角形的外角的性质,圆周角定理等知识,解题的关键是理解题意,灵活运用所学知识解决问题.
6、B
【分析】
连接AC,根据菱形的性质得到△ABC、△ACD是等边三角形,求出∠BCD=120°,再根据圆周角定理即可求解.
【详解】
如图,连接AC
∴AC=AB=AD
∵四边形ABCD是菱形
∴AB=BC=AD=CD=AC
∴△ABC、△ACD是等边三角形
∴∠ACB=∠ACD=60°
∴∠BCD=120°
∵优弧
∴∠BED=∠BCD=120°
故选B.
( http: / / www.21cnjy.com / )
【点睛】
此题主要考查圆内角度求解,解题的关键是熟知菱形的性质及圆周角定理.
7、C
【分析】
由题意直接根据圆周角定理进行分析即可得出答案.
【详解】
解:∵∠ABC和∠AOC是弧AC所对的圆周角和圆心角,,
∴∠ABC=∠AOC=.
故选:C.
【点睛】
本题考查圆周角定理,注意掌握同弧(等弧)所对的圆周角是圆心角的一半.
8、A
【分析】
根据直径所对的圆角为直角,可得 ,再由直角三角形中,30°角所对的直角边等于斜边的一半,即可求解.21教育网
【详解】
解:∵AB是⊙O的直径,
∴ ,
∵∠BAC=30°,BC=2,
∴.
故选:A
【点睛】
本题主要考查了直径所对的圆角, ( http: / / www.21cnjy.com )直角三角形的性质,熟练掌握直径所对的圆角为直角;直角三角形中,30°角所对的直角边等于斜边的一半是解题的关键.
9、B
【分析】
阴影部分的面积=扇形扇形,根据旋转性质以及直角三角形的性质,分别求出对应扇形的面积以及的面积,最后即可求出阴影部分的面积.
【详解】
解:由图可知:阴影部分的面积=扇形扇形,
由旋转性质可知:,,
,,
在中,,,,
,,
有勾股定理可知:,
阴影部分的面积=扇形扇形
.
故选:B.
【点睛】
本题主要是考查了旋转性质以及扇形面积公式,熟练利用旋转性质,得到对应扇形的半径和圆心角度数,利用扇形公式求解面积,这是解决本题的关键.
10、D
【分析】
连接CD,由直角三角形斜边中线定理可得CD=BD,然后可得△CDB是等边三角形,则有BD=BC=5cm,进而根据勾股定理可求解.
【详解】
解:连接CD,如图所示:
( http: / / www.21cnjy.com / )
∵点D是AB的中点,,,
∴,
∵,
∴,
在Rt△ACB中,由勾股定理可得;
故选D.
【点睛】
本题主要考查圆的基本性质、直角三角形斜边中线定理及勾股定理,熟练掌握圆的基本性质、直角三角形斜边中线定理及勾股定理是解题的关键.
二、填空题
1、8
【分析】
如图所示,连接OC,由垂径定理可得,再由勾股定理求出,即可得到答案.
【详解】
解:如图所示,连接OC,
∵AB为⊙O的直径,弦CD⊥AB于点H,CD=8,
∴,∠OHC=90°,
∵OC=OA=5,
∴,
∴AH=OA+OH=8,
故答案为:8.
( http: / / www.21cnjy.com / )
【点睛】
本题主要考查了勾股定理和垂径定理,解题的关键在于能够熟练掌握垂径定理.
2、24
【分析】
连接OA,过点O作OD⊥AB交AB于点C交⊙O于D,再根据勾股定理求出AC的长,进而可得出AB的长.
【详解】
解:连接OA,过点O作OD⊥AB交AB于点C交⊙O于D.
( http: / / www.21cnjy.com / )
∵OC⊥AB,
∴AC=CB,
∵OA=OD=13cm,CD=8cm,
∴OC=OD﹣CD=5(cm),
∴,
∴AB=2AC=24(cm),
故答案为:24.
【点睛】
本题主要考查垂径定理,掌握垂径定理和勾股定理是解题的关键.
3、②④
【分析】
将所给四个条件逐一判断即可得出结论.
【详解】
解:在中,
①当∠BAC > 60°时,若时,点E与点A重合,不符合题意,故①不满足;
②当∠ABC时,点E与点A重合,不符合题意,当∠ABC时,点E与点O不关于AD对称,当时,点E关于直线AD的对称点在线段OA上,
所以,当45° < ∠ABC < 60°时,点E关于直线AD的对称点在线段OA上,故②满足条件;
③当时,点E关于直线AD的对称点在线段OA上,故③不满足条件;
④当AB < DE < AB时,点E关于直线AD的对称点在线段OA上,故④满足条件;
所以,要使得与AC边的交点E关于直线AD的对称点在线段OA上(不与端点重合),需满足的条件可以是45° < ∠ABC < 60°或AB < DE < AB21世纪教育网版权所有
故答案为②④
【点睛】
本题考查了圆周角定理,正确判断出每种情况是解答本题的关键.
4、60
【分析】
先根据圆的切线的性质可得,从而可得,再根据切线长定理可得,然后根据等边三角形的判定与性质即可得.
【详解】
解:是的切线,
,
,
,
,
是等边三角形,
,
故答案为:60.
【点睛】
本题考查了圆的切线的性质、切线长定理等知识点,熟练掌握圆的切线的性质是解题关键.
5、①②④
【分析】
连接OM,由切线的性质可得,继而得,再根据平行线的性质以及等边对等角即可求得,由此可判断①;通过证明,根据相似三角形的对应边成比例可判断②;求出,利用弧长公式求得的长可判断③;由,,,可得,继而可得,,进而有,在中,利用勾股定理求出PD的长,可得,由此可判断④.
【详解】
解:连接OM,
( http: / / www.21cnjy.com / )
∵PE为的切线,
∴,
∵,
∴,
∴,
∵,,
∴,
即AM平分,故①正确;
∵AB为的直径,
∴,
∵,,
∴,
∴,
∴,故②正确;
∵,
∴,
∵,
∴,
∴的长为,故③错误;
∵,,,
∴,
∴,
∴,
∴,
又∵,,,
∴,
又∵,
∴,
设,则,
∴,
在中,,
∴,
∴,
由①可得,
,
故④正确,
故答案为:①②④.
【点睛】
本题考查了切线的性质,平行线分线段成比例定理,相似三角形的判定与性质,勾股定理等,正确添加辅助线,熟练掌握和灵活运用相关知识是解题的关键.www.21-cn-jy.com
三、解答题
1、(1)见解析;(2)
【分析】
(1)连接OC.根据半径相等,利用切线的性质和等角的余角相等证得∠ECF=∠EFC,即可得到结论;
(2)设BF=BE=x,在Rt△OCE中,利用勾股定理可求得x=2,再在Rt△ODF中,利用勾股定理即可求解.21教育名师原创作品
【详解】
(1)证明:如图,连接OC.
( http: / / www.21cnjy.com / )
∵CE切⊙O于点C,
∴OC⊥CE,
∴∠OCF+∠ECF=90°,
∵OD⊥AB,
∴∠D+∠DFO=90°,
∵OC=OD,
∴∠D=∠OCD,
∴∠ECF=∠OFD
又∵∠OFD=∠EFC
∴∠ECF=∠EFC,
∴EC=EF;
(2)解: ∵BF=BE,
设BF=BE=x,则EC=EF=2x,OE=3+x,
在Rt△OCE中,OC2+CE2=OE2,
∴32+(2x)2=(3+x)2,
解得x1=0(舍),x2=2,
∴OF=OB-FB=1,
在Rt△ODF中,.
【点睛】
本题考查了切线的性质,勾股定理,解一元二次方程等知识,解题的关键是灵活运用所学知识解决问题.
2、(1)① 2;② ;(2)t的值为3或;(3)π
【分析】
(1)①根据定义解答即可;②分别找出的最大值,再根据定义判断即可;
(2) 如图所示,正方形ABCD上的任意两点间距离的最大值为.若点E(t,3)是正方形ABCD的“倍点”,则点E到ABCD上的点的最大距离恰好为. 分, 和【来源:21·世纪·教育·网】
分别讨论即可求解;
(3)分线段MN在内部和在外部两种情况讨论即可.
【详解】
(1)①圆上两点之间的最大距离是直径2,根据定义可知d= 2,
故答案为:2;
②由图可知,故不是图形W的“倍点”; ,故不是图形W的“倍点”;,当Q(1,0)时,=2d,故P为图形W的“倍点”;【出处:21教育名师】
故答案为:;
(2)如图所示,正方形ABCD上的任意两点间距离的最大值为.
( http: / / www.21cnjy.com / )
依题意,若点E(t,3)是正方形ABCD的“倍点”,则点E到ABCD上的点的最大距离恰好为.
当时,点E到ABCD上的点的最大距离为EC的长. 取点H(1,3),则CH⊥EH且CH=4,此时可求得EH=4,从而点E的坐标为,即;
当时,点E到ABCD上的点的最大距离为ED的长.由对称性可得点E的坐标为,即.
当时,显然不符合题意.
综上,t的值为3或.
(3)MN上d=2,2d=4,
当线段MN在内部时,T组成的图形为半径为4的圆,,
当线段MN在外部时,T组成的图形为半径为8的圆,,
故点T所构成的图形的面积为或.
【点睛】
此题考查考查了一次函数的性质,图形上两点间的“极大距离”等知识,解题的关键是理解题意,学会寻找特殊位置解决数学问题,属于中考压轴题.
3、(1)见解析;(2)
【分析】
(1)根据点O的坐标确定直角坐标系,根据旋转的性质确定点A1、B1,顺次连线即可得到△OA1B1;
(2)利用弧长公式计算即可.
【详解】
解:(1)如图,△OA1B1即为所求三角形;
( http: / / www.21cnjy.com / )
(2)旋转过程中点B走过的路径的长=.
【点睛】
此题考查了旋转作图,弧长的计算公式,正确掌握旋转的性质及弧长的计算公式是解题的关键.
4、(1)作图见解析;(2) 在同圆中,等弧所对的圆周角相等
【分析】
(1)根据题干的作图步骤依次作图即可;
(2)由作图可得,证明,利用圆周角定理可得,从而可得答案.
【详解】
解:(1)如图,直线BD就是所求作的直线
( http: / / www.21cnjy.com / )
(2)证明:连接AD,
∵点A,B,C,D在上,,
∴.
∴(在同圆中,等弧所对的圆周角相等).
∴.
故答案为: 在同圆中,等弧所对的圆周角相等
【点睛】
本题考查的是作线段的垂直平分线,三角形的外接圆,平行线的作图,圆周角定理的应用,掌握“圆周角定理”是理解作图的关键.【版权所有:21教育】
5、(1)见解析;(2)同弧所对的圆周角等于圆心角的一半;线段垂直平分线上的点到这条线段两个端点的距离相等
【分析】
(1)根据题意补全图形;
(2)根据同一个圆中,同弧所对的圆周角等于圆心角的一半,及垂直平分线上的点到两端点的距离相等即可.
【详解】
(1)作图正确;
( http: / / www.21cnjy.com / )
(2)证明:连接OA,OB.
∵OA=OB=AB,
∴OAB是等边三角形.
∴.
∵A,B,C在⊙O上,
∴∠ACB=∠AOB(同弧所对的圆周角等于圆心角的一半)(填推理的依据).
∴.
由作图可知直线OE是线段AB的垂直平分线,
∴AC=BC(线段垂直平分线上的点到这条线段两个端点的距离相等)(填推理的依据).
∴ABC就是所求作的三角形,
故答案是:同弧所对的圆周角等于圆心角的一半;线段垂直平分线上的点到这条线段两个端点的距离相等.
【点睛】
本题是圆的综合题、作图、考查了圆周角定理、垂直平分线、等腰三角形,解题的关键是熟练掌握圆周角定理及作图的基本能力.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
九年级数学第二学期第二十七章圆与正多边形专项测试
考试时间:90分钟;命题人:数学教研组
考生注意:
1、本卷分第I卷(选择题)和第Ⅱ卷(非选择题)两部分,满分100分,考试时间90分钟
2、答卷前,考生务必用0.5毫米黑色签字笔将自己的姓名、班级填写在试卷规定位置上
3、答案必须写在试卷各个题目指定区域内相 ( http: / / www.21cnjy.com )应的位置,如需改动,先划掉原来的答案,然后再写上新的答案;不准使用涂改液、胶带纸、修正带,不按以上要求作答的答案无效。21*cnjy*com
第I卷(选择题 30分)
一、单选题(10小题,每小题3分,共计30分)
1、如图,中,,,,点为的中点,以为圆心,长为半径作半圆,交于点,则图中阴影部分的面积是( )
( http: / / www.21cnjy.com / )
A. B. C. D.
2、如图,AB是⊙O的直径,BD与⊙ ( http: / / www.21cnjy.com )O相切于点B,点C是⊙O上一点,连接AC并延长,交BD于点D,连接OC,BC,若∠BOC=50°,则∠D的度数为( )
( http: / / www.21cnjy.com / )
A.50° B.55° C.65° D.75°
3、如图,AB是的直径,的弦DC的延长线与AB的延长线相交于点P,于点E,,,则阴影部分的面积为( )
( http: / / www.21cnjy.com / )
A. B. C. D.
4、如图,ABC内接于⊙O,,BD为⊙O的直径,且BD=2,则DC=( )
( http: / / www.21cnjy.com / )
A.1 B. C. D.
5、如图,有一个弓形的暗礁区,弓形所含的圆周角,船在航行时,为保证不进入暗礁区,则船到两个灯塔A,B的张角应满足的条件是( )
( http: / / www.21cnjy.com / )
A. B.
C. D.
6、如图,菱形ABCD的顶点B,C,D均在⊙A上,点E在弧BD上,则∠BED的度数为( )
( http: / / www.21cnjy.com / )
A.90° B.120° C.135° D.150°
7、如图,中,,则等于( )
( http: / / www.21cnjy.com / )
A. B. C. D.
8、如图,AB是⊙O的直径,点C是⊙O上一点,若∠BAC=30°,BC=2,则AB的长为( )
( http: / / www.21cnjy.com / )
A.4 B.6 C.8 D.10
9、如图,在中,,,.将绕点按逆时针方向旋转后得到,则图中阴影部分面积为( )
( http: / / www.21cnjy.com / )
A. B. C. D.
10、如图,在中,,,若以点为圆心,的长为半径的圆恰好经过的中点,则的长等于( )
( http: / / www.21cnjy.com / )
A. B. C. D.
第Ⅱ卷(非选择题 70分)
二、填空题(5小题,每小题4分,共计20分)
1、如图,为的直径,弦于点,,,则的长为________.
( http: / / www.21cnjy.com / )
2、往直径为26cm的圆柱形容器内装入一些水以后,截面如图所示,若水的最大深度为8cm,则水面AB的宽度为___cm.
( http: / / www.21cnjy.com / )
3、在△ABC中,AB = AC,以AB为直径的圆O交BC边于点D.要使得圆O与AC边的交点E关于直线AD的对称点在线段OA上(不与端点重合),需满足的条件可以是 _________ .(写出所有正确答案的序号)①∠BAC > 60°;②45° < ∠ABC < 60°;③BD > AB;④AB < DE < AB.
4、如图,PA、PB是⊙O的切线,A、B为切点,∠OAB=30°.则∠APB=________度;
( http: / / www.21cnjy.com / )
5、如图AB为⊙O的直径, ( http: / / www.21cnjy.com )点P为AB延长线上的点,过点P作⊙O的切线PE,切点为M,过A、B两点分别作PE垂线AC、BD,垂足分别为C、D,连接AM,则下列结论正确的是______(写所有正确论的号)
①AM平分∠CAB;②;③若AB=4,∠APE=30°,则的长为;④若AC=3BD,则有tan∠MAP=.2-1-c-n-j-y
( http: / / www.21cnjy.com / )
三、解答题(5小题,每小题10分,共计50分)
1、如图,为⊙O的直径,半径于O,⊙O的弦与相交于点F,⊙O的切线交的延长线于点E.
( http: / / www.21cnjy.com / )
(1)求证:;
(2)若⊙O的半径长为3,且,求的长.
2、在平面直角坐标系xOy中,图 ( http: / / www.21cnjy.com )形W上任意两点间的距离有最大值,将这个最大值记为d.对点P及图形W给出如下定义:点Q为图形W上任意一点,若P,Q两点间的距离有最大值,且最大值恰好为2d,则称点P为图形W的“倍点”.
(1)如图1,图形W是半径为1的⊙O.
①图形W上任意两点间的距离的最大值d为_________;
②在点(0,2) ,(3,3),(,0)中,⊙O的“倍点”是________;
(2)如图2,图形W是中心在原点的正方形ABCD,已知点A(,1),若点E(,3) 是正方形ABCD的“倍点”,求的值;
(3)图形W是长为2的线段MN,T为MN的中点,若在半径为6的⊙O上存在MN的“倍点”,直接写出满足条件的点T所构成的图形的面积.
( http: / / www.21cnjy.com / )
3、如图,点O,B的坐标分别是(0,0),(3,0).将△OAB绕点O逆时针旋转90°,得到△OA1B1.
(1)画出平面直角坐标系和三角形△OA1B1;
(2)求旋转过程中点B走过的路径的长.
( http: / / www.21cnjy.com / )
4、下面是小石设计的“过三角形一个顶点作其对边的平行线”的尺规作图过程.
已知:如图,.
( http: / / www.21cnjy.com / )
求作:直线BD,使得.
作法:如图,
( http: / / www.21cnjy.com / )
①分别作线段AC,BC的垂直平分线,,两直线交于点O;
②以点O为圆心,OA长为半径作圆;
③以点A为圆心,BC长为半径作孤,交于点D;
④作直线BD.所以直线BD就是所求作的直线.
根据小石设计的尺规作图过程,
(1)使用直尺和圆规,补全图形;(保留作图痕迹)
(2)完成下面的证明.
证明:连接AD,
∵点A,B,C,D在上,,
∴______.
∴(______)(填推理的依据).
∴.
5、已知:A,B是直线l上的两点.
求作:ABC,使得点C在直线l上方,且AC=BC,.
作法:①分别以A,B为圆心,AB长为半径画弧,在直线l上方交于点O,在直线l下方交于点E;
②以点O为圆心,OA长为半径画圆;
③作直线OE与直线l上方的⊙O交于点C;
④连接AC,BC.ABC就是所求作的三角形.
(1)使用直尺和圆规,依作法补全图形(保留作图痕迹);
(2)完成下面的证明.
证明:连接OA,OB.
∵OA=OB=AB,
∴OAB是等边三角形.
∴.
∵A,B,C在⊙O上,
∴∠ACB=∠AOB( )(填推理的依据).
∴.
由作图可知直线OE是线段AB的垂直平分线,
∴AC=BC( )(填推理的依据).
∴ABC就是所求作的三角形.
-参考答案-
一、单选题
1、A
【分析】
连接OD,BD,作OH⊥CD交CD于点H,首先根据勾股定理求出BC的长度,然后利用等面积法求出BD的长度,进而得到是等边三角形,,然后根据30°角直角三角形的性质求出OH的长度,最后根据进行计算即可.21cnjy.com
【详解】
解:如图所示,连接OD,BD,作OH⊥CD交CD于点H
( http: / / www.21cnjy.com / )
∵,,
∴在中,
∵点为的中点,以为圆心,长为半径作半圆
∴是圆的直径,
∴
∴,即
解得:
又∵
∴
∴是等边三角形
∴
∴
∵OH⊥CD
∴,
∴.
故选:A.
【点睛】
本题考查了30°角直角三角形的性质,等 ( http: / / www.21cnjy.com )边三角形的性质和判定,扇形面积,勾股定理等知识,正确添加辅助线,熟练掌握和灵活运用相关知识是解题的关键.21·cn·jy·com
2、C
【分析】
首先证明∠ABD=90°,由∠BOC=50°,根据圆周角定理求出∠A的度数即可解决问题.
【详解】
解:∵BD是切线,
∴BD⊥AB,
∴∠ABD=90°,
∵∠BOC=50°,
∴∠A=∠BOC=25°,
∴∠D=90°﹣∠A=65°,
故选:C.
【点睛】
本题考查的是切线的性质、圆周角定理,解题的关键是灵活应用所学知识解决问题,属于中考常考题型.
3、B
【分析】
由垂径定理可知,AE=CE,则阴影部分的面积等于扇形AOD的面积,求出,然后利用扇形面积公式,即可求出答案.21·世纪*教育网
【详解】
解:根据题意,如图:
( http: / / www.21cnjy.com / )
∵AB是的直径,OD是半径,,
∴AE=CE,
∴阴影CED的面积等于AED的面积,
∴,
∵,,
∴,
∴;
故选:B
【点睛】
本题考查了求扇形的面积,垂径定理,解题的关键是掌握所学的知识,正确利用扇形的面积公式进行计算.
4、C
【分析】
根据三角形内角和定理求得,根据同弧所对的圆周角相等可得,根据直径所对的圆周角是直角,含30度角的直角三角形的性质,勾股定理即可求得的长2·1·c·n·j·y
【详解】
解:
为⊙O的直径,
在,, BD=2,
故选C
【点睛】
本题考查了三角形内角和定理,同弧所对的圆周角相等,直径所对的圆周角是直角,勾股定理,含30度角的直角三角形的性质,求得是解题的关键.www-2-1-cnjy-com
5、D
【分析】
本题利用了三角形外角与内角的关系和圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.21*cnjy*com
【详解】
如图,AS交圆于点E,连接EB,
( http: / / www.21cnjy.com / )
由圆周角定理知,∠AEB=∠C=50°,而∠AEB是△SEB的一个外角,由∠AEB>∠S,即当∠S<50°时船不进入暗礁区.【来源:21cnj*y.co*m】
所以,两个灯塔的张角∠ASB应满足的条件是∠ASB<50°.
∴cos∠ASB>cos50°,
故选:D.
【点睛】
本题考查三角形的外角的性质,圆周角定理等知识,解题的关键是理解题意,灵活运用所学知识解决问题.
6、B
【分析】
连接AC,根据菱形的性质得到△ABC、△ACD是等边三角形,求出∠BCD=120°,再根据圆周角定理即可求解.
【详解】
如图,连接AC
∴AC=AB=AD
∵四边形ABCD是菱形
∴AB=BC=AD=CD=AC
∴△ABC、△ACD是等边三角形
∴∠ACB=∠ACD=60°
∴∠BCD=120°
∵优弧
∴∠BED=∠BCD=120°
故选B.
( http: / / www.21cnjy.com / )
【点睛】
此题主要考查圆内角度求解,解题的关键是熟知菱形的性质及圆周角定理.
7、C
【分析】
由题意直接根据圆周角定理进行分析即可得出答案.
【详解】
解:∵∠ABC和∠AOC是弧AC所对的圆周角和圆心角,,
∴∠ABC=∠AOC=.
故选:C.
【点睛】
本题考查圆周角定理,注意掌握同弧(等弧)所对的圆周角是圆心角的一半.
8、A
【分析】
根据直径所对的圆角为直角,可得 ,再由直角三角形中,30°角所对的直角边等于斜边的一半,即可求解.21教育网
【详解】
解:∵AB是⊙O的直径,
∴ ,
∵∠BAC=30°,BC=2,
∴.
故选:A
【点睛】
本题主要考查了直径所对的圆角, ( http: / / www.21cnjy.com )直角三角形的性质,熟练掌握直径所对的圆角为直角;直角三角形中,30°角所对的直角边等于斜边的一半是解题的关键.
9、B
【分析】
阴影部分的面积=扇形扇形,根据旋转性质以及直角三角形的性质,分别求出对应扇形的面积以及的面积,最后即可求出阴影部分的面积.
【详解】
解:由图可知:阴影部分的面积=扇形扇形,
由旋转性质可知:,,
,,
在中,,,,
,,
有勾股定理可知:,
阴影部分的面积=扇形扇形
.
故选:B.
【点睛】
本题主要是考查了旋转性质以及扇形面积公式,熟练利用旋转性质,得到对应扇形的半径和圆心角度数,利用扇形公式求解面积,这是解决本题的关键.
10、D
【分析】
连接CD,由直角三角形斜边中线定理可得CD=BD,然后可得△CDB是等边三角形,则有BD=BC=5cm,进而根据勾股定理可求解.
【详解】
解:连接CD,如图所示:
( http: / / www.21cnjy.com / )
∵点D是AB的中点,,,
∴,
∵,
∴,
在Rt△ACB中,由勾股定理可得;
故选D.
【点睛】
本题主要考查圆的基本性质、直角三角形斜边中线定理及勾股定理,熟练掌握圆的基本性质、直角三角形斜边中线定理及勾股定理是解题的关键.
二、填空题
1、8
【分析】
如图所示,连接OC,由垂径定理可得,再由勾股定理求出,即可得到答案.
【详解】
解:如图所示,连接OC,
∵AB为⊙O的直径,弦CD⊥AB于点H,CD=8,
∴,∠OHC=90°,
∵OC=OA=5,
∴,
∴AH=OA+OH=8,
故答案为:8.
( http: / / www.21cnjy.com / )
【点睛】
本题主要考查了勾股定理和垂径定理,解题的关键在于能够熟练掌握垂径定理.
2、24
【分析】
连接OA,过点O作OD⊥AB交AB于点C交⊙O于D,再根据勾股定理求出AC的长,进而可得出AB的长.
【详解】
解:连接OA,过点O作OD⊥AB交AB于点C交⊙O于D.
( http: / / www.21cnjy.com / )
∵OC⊥AB,
∴AC=CB,
∵OA=OD=13cm,CD=8cm,
∴OC=OD﹣CD=5(cm),
∴,
∴AB=2AC=24(cm),
故答案为:24.
【点睛】
本题主要考查垂径定理,掌握垂径定理和勾股定理是解题的关键.
3、②④
【分析】
将所给四个条件逐一判断即可得出结论.
【详解】
解:在中,
①当∠BAC > 60°时,若时,点E与点A重合,不符合题意,故①不满足;
②当∠ABC时,点E与点A重合,不符合题意,当∠ABC时,点E与点O不关于AD对称,当时,点E关于直线AD的对称点在线段OA上,
所以,当45° < ∠ABC < 60°时,点E关于直线AD的对称点在线段OA上,故②满足条件;
③当时,点E关于直线AD的对称点在线段OA上,故③不满足条件;
④当AB < DE < AB时,点E关于直线AD的对称点在线段OA上,故④满足条件;
所以,要使得与AC边的交点E关于直线AD的对称点在线段OA上(不与端点重合),需满足的条件可以是45° < ∠ABC < 60°或AB < DE < AB21世纪教育网版权所有
故答案为②④
【点睛】
本题考查了圆周角定理,正确判断出每种情况是解答本题的关键.
4、60
【分析】
先根据圆的切线的性质可得,从而可得,再根据切线长定理可得,然后根据等边三角形的判定与性质即可得.
【详解】
解:是的切线,
,
,
,
,
是等边三角形,
,
故答案为:60.
【点睛】
本题考查了圆的切线的性质、切线长定理等知识点,熟练掌握圆的切线的性质是解题关键.
5、①②④
【分析】
连接OM,由切线的性质可得,继而得,再根据平行线的性质以及等边对等角即可求得,由此可判断①;通过证明,根据相似三角形的对应边成比例可判断②;求出,利用弧长公式求得的长可判断③;由,,,可得,继而可得,,进而有,在中,利用勾股定理求出PD的长,可得,由此可判断④.
【详解】
解:连接OM,
( http: / / www.21cnjy.com / )
∵PE为的切线,
∴,
∵,
∴,
∴,
∵,,
∴,
即AM平分,故①正确;
∵AB为的直径,
∴,
∵,,
∴,
∴,
∴,故②正确;
∵,
∴,
∵,
∴,
∴的长为,故③错误;
∵,,,
∴,
∴,
∴,
∴,
又∵,,,
∴,
又∵,
∴,
设,则,
∴,
在中,,
∴,
∴,
由①可得,
,
故④正确,
故答案为:①②④.
【点睛】
本题考查了切线的性质,平行线分线段成比例定理,相似三角形的判定与性质,勾股定理等,正确添加辅助线,熟练掌握和灵活运用相关知识是解题的关键.www.21-cn-jy.com
三、解答题
1、(1)见解析;(2)
【分析】
(1)连接OC.根据半径相等,利用切线的性质和等角的余角相等证得∠ECF=∠EFC,即可得到结论;
(2)设BF=BE=x,在Rt△OCE中,利用勾股定理可求得x=2,再在Rt△ODF中,利用勾股定理即可求解.21教育名师原创作品
【详解】
(1)证明:如图,连接OC.
( http: / / www.21cnjy.com / )
∵CE切⊙O于点C,
∴OC⊥CE,
∴∠OCF+∠ECF=90°,
∵OD⊥AB,
∴∠D+∠DFO=90°,
∵OC=OD,
∴∠D=∠OCD,
∴∠ECF=∠OFD
又∵∠OFD=∠EFC
∴∠ECF=∠EFC,
∴EC=EF;
(2)解: ∵BF=BE,
设BF=BE=x,则EC=EF=2x,OE=3+x,
在Rt△OCE中,OC2+CE2=OE2,
∴32+(2x)2=(3+x)2,
解得x1=0(舍),x2=2,
∴OF=OB-FB=1,
在Rt△ODF中,.
【点睛】
本题考查了切线的性质,勾股定理,解一元二次方程等知识,解题的关键是灵活运用所学知识解决问题.
2、(1)① 2;② ;(2)t的值为3或;(3)π
【分析】
(1)①根据定义解答即可;②分别找出的最大值,再根据定义判断即可;
(2) 如图所示,正方形ABCD上的任意两点间距离的最大值为.若点E(t,3)是正方形ABCD的“倍点”,则点E到ABCD上的点的最大距离恰好为. 分, 和【来源:21·世纪·教育·网】
分别讨论即可求解;
(3)分线段MN在内部和在外部两种情况讨论即可.
【详解】
(1)①圆上两点之间的最大距离是直径2,根据定义可知d= 2,
故答案为:2;
②由图可知,故不是图形W的“倍点”; ,故不是图形W的“倍点”;,当Q(1,0)时,=2d,故P为图形W的“倍点”;【出处:21教育名师】
故答案为:;
(2)如图所示,正方形ABCD上的任意两点间距离的最大值为.
( http: / / www.21cnjy.com / )
依题意,若点E(t,3)是正方形ABCD的“倍点”,则点E到ABCD上的点的最大距离恰好为.
当时,点E到ABCD上的点的最大距离为EC的长. 取点H(1,3),则CH⊥EH且CH=4,此时可求得EH=4,从而点E的坐标为,即;
当时,点E到ABCD上的点的最大距离为ED的长.由对称性可得点E的坐标为,即.
当时,显然不符合题意.
综上,t的值为3或.
(3)MN上d=2,2d=4,
当线段MN在内部时,T组成的图形为半径为4的圆,,
当线段MN在外部时,T组成的图形为半径为8的圆,,
故点T所构成的图形的面积为或.
【点睛】
此题考查考查了一次函数的性质,图形上两点间的“极大距离”等知识,解题的关键是理解题意,学会寻找特殊位置解决数学问题,属于中考压轴题.
3、(1)见解析;(2)
【分析】
(1)根据点O的坐标确定直角坐标系,根据旋转的性质确定点A1、B1,顺次连线即可得到△OA1B1;
(2)利用弧长公式计算即可.
【详解】
解:(1)如图,△OA1B1即为所求三角形;
( http: / / www.21cnjy.com / )
(2)旋转过程中点B走过的路径的长=.
【点睛】
此题考查了旋转作图,弧长的计算公式,正确掌握旋转的性质及弧长的计算公式是解题的关键.
4、(1)作图见解析;(2) 在同圆中,等弧所对的圆周角相等
【分析】
(1)根据题干的作图步骤依次作图即可;
(2)由作图可得,证明,利用圆周角定理可得,从而可得答案.
【详解】
解:(1)如图,直线BD就是所求作的直线
( http: / / www.21cnjy.com / )
(2)证明:连接AD,
∵点A,B,C,D在上,,
∴.
∴(在同圆中,等弧所对的圆周角相等).
∴.
故答案为: 在同圆中,等弧所对的圆周角相等
【点睛】
本题考查的是作线段的垂直平分线,三角形的外接圆,平行线的作图,圆周角定理的应用,掌握“圆周角定理”是理解作图的关键.【版权所有:21教育】
5、(1)见解析;(2)同弧所对的圆周角等于圆心角的一半;线段垂直平分线上的点到这条线段两个端点的距离相等
【分析】
(1)根据题意补全图形;
(2)根据同一个圆中,同弧所对的圆周角等于圆心角的一半,及垂直平分线上的点到两端点的距离相等即可.
【详解】
(1)作图正确;
( http: / / www.21cnjy.com / )
(2)证明:连接OA,OB.
∵OA=OB=AB,
∴OAB是等边三角形.
∴.
∵A,B,C在⊙O上,
∴∠ACB=∠AOB(同弧所对的圆周角等于圆心角的一半)(填推理的依据).
∴.
由作图可知直线OE是线段AB的垂直平分线,
∴AC=BC(线段垂直平分线上的点到这条线段两个端点的距离相等)(填推理的依据).
∴ABC就是所求作的三角形,
故答案是:同弧所对的圆周角等于圆心角的一半;线段垂直平分线上的点到这条线段两个端点的距离相等.
【点睛】
本题是圆的综合题、作图、考查了圆周角定理、垂直平分线、等腰三角形,解题的关键是熟练掌握圆周角定理及作图的基本能力.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
