【强化训练】沪教版(上海)九下 第二十七章 圆与正多边形章节练习试题(含解析)
文档属性
| 名称 | 【强化训练】沪教版(上海)九下 第二十七章 圆与正多边形章节练习试题(含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 2.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-22 08:38:22 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
九年级数学第二学期第二十七章圆与正多边形章节练习
考试时间:90分钟;命题人:数学教研组
考生注意:
1、本卷分第I卷(选择题)和第Ⅱ卷(非选择题)两部分,满分100分,考试时间90分钟
2、答卷前,考生务必用0.5毫米黑色签字笔将自己的姓名、班级填写在试卷规定位置上
3、答案必须写在试卷各个题 ( http: / / www.21cnjy.com )目指定区域内相应的位置,如需改动,先划掉原来的答案,然后再写上新的答案;不准使用涂改液、胶带纸、修正带,不按以上要求作答的答案无效。www-2-1-cnjy-com
第I卷(选择题 30分)
一、单选题(10小题,每小题3分,共计30分)
1、如图,已知AB是⊙O的直径,CD是弦,若∠BCD=36°,则∠ABD等于( )
( http: / / www.21cnjy.com / )
A.54° B.56° C.64° D.66°
2、如图,有一个亭子,它的地基是边长为4m的正六边形,则地基的面积为( )
( http: / / www.21cnjy.com / )
A.4m2 B.12m2 C.24m2 D.24m2
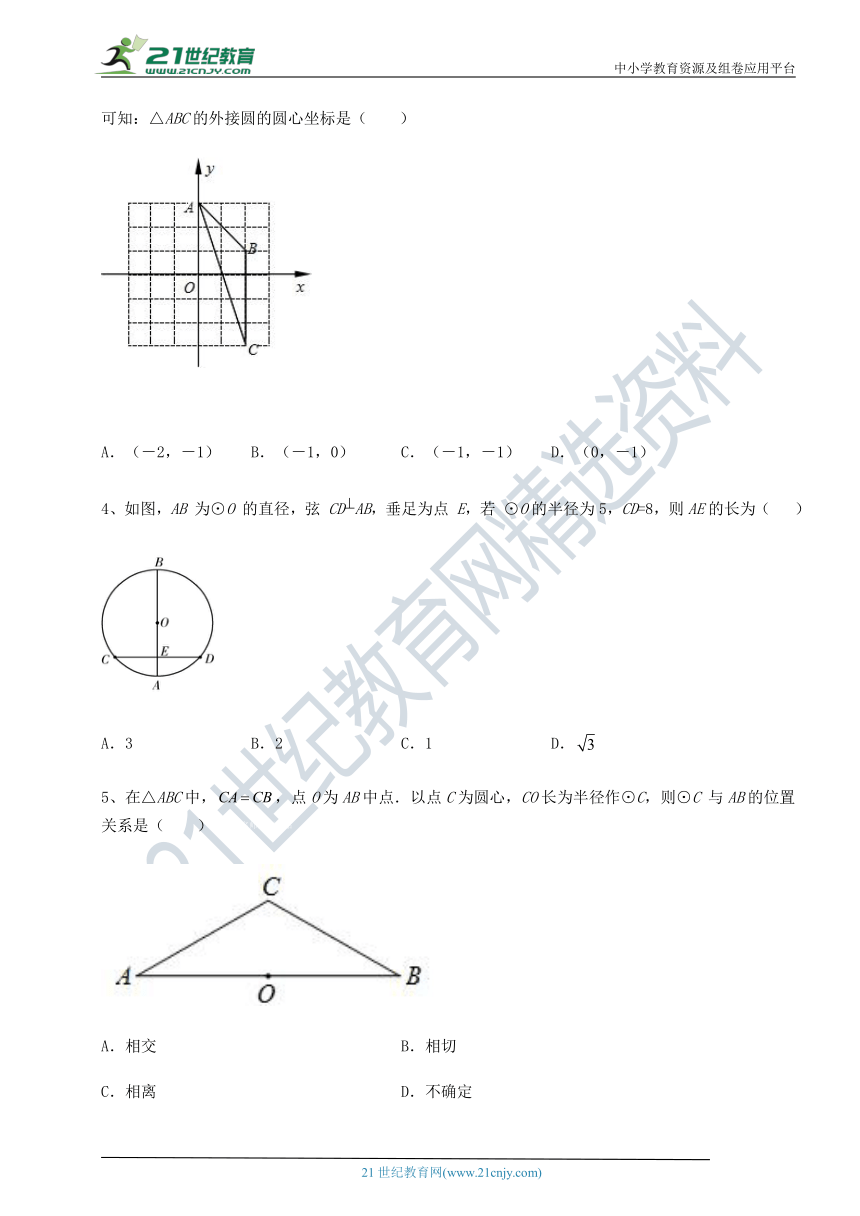
3、如图,在平面直角坐标系xOy中,点A ( http: / / www.21cnjy.com )(0,3),点B(2,1),点C(2,-3).则经画图操作可知:△ABC的外接圆的圆心坐标是( )2-1-c-n-j-y
( http: / / www.21cnjy.com / )
A.(-2,-1) B.(-1,0) C.(-1,-1) D.(0,-1)
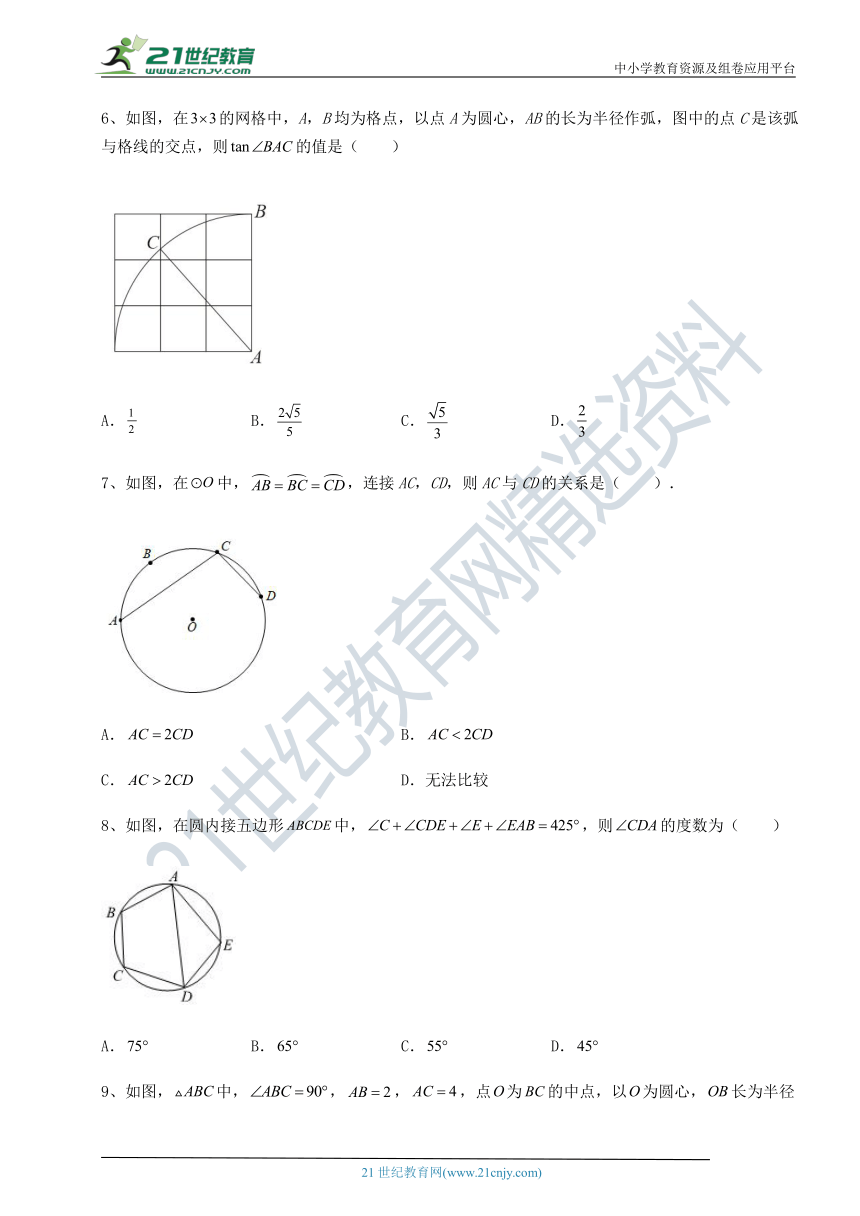
4、如图,AB 为⊙O 的直径,弦 CDAB,垂足为点 E,若 ⊙O的半径为5,CD=8,则AE的长为( )
( http: / / www.21cnjy.com / )
A.3 B.2 C.1 D.
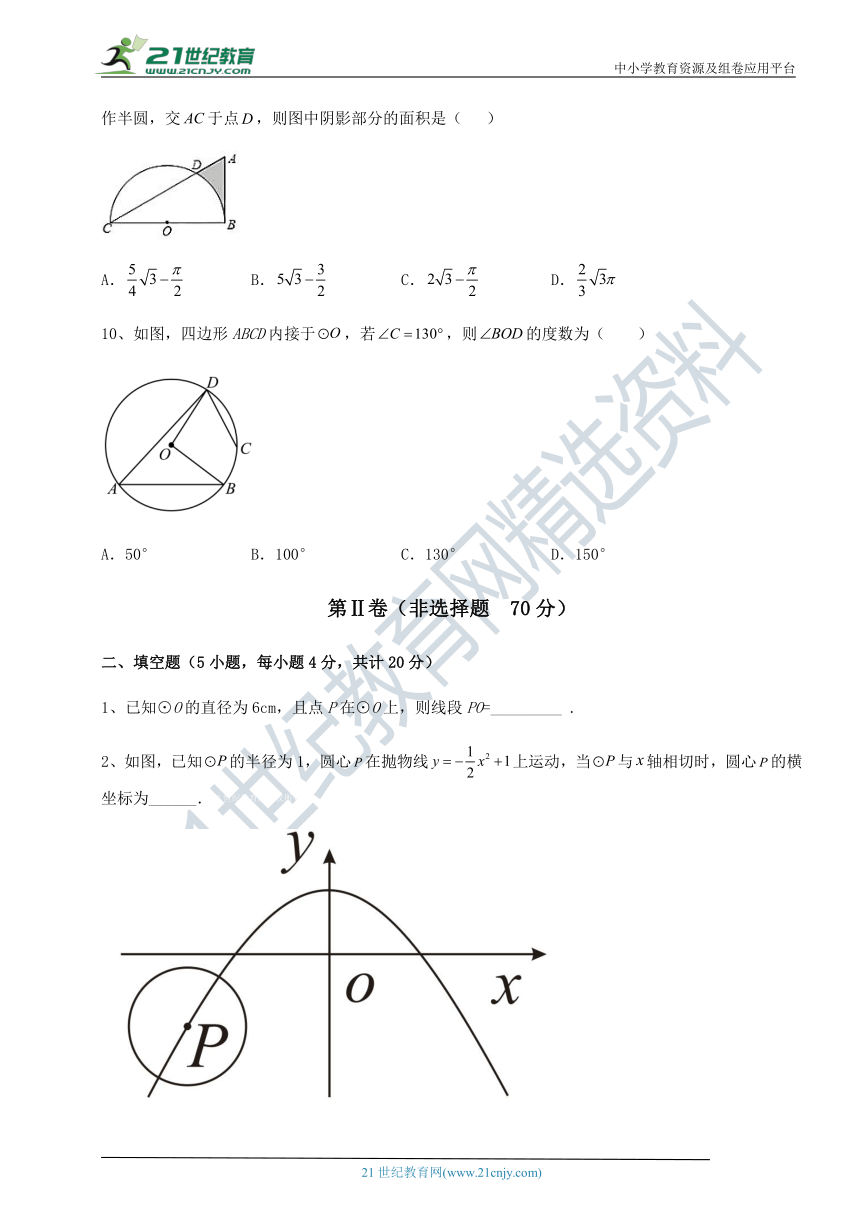
5、在△ABC中,,点O为AB中点.以点C为圆心,CO长为半径作⊙C,则⊙C 与AB的位置关系是( )21教育名师原创作品
( http: / / www.21cnjy.com / )
A.相交 B.相切
C.相离 D.不确定
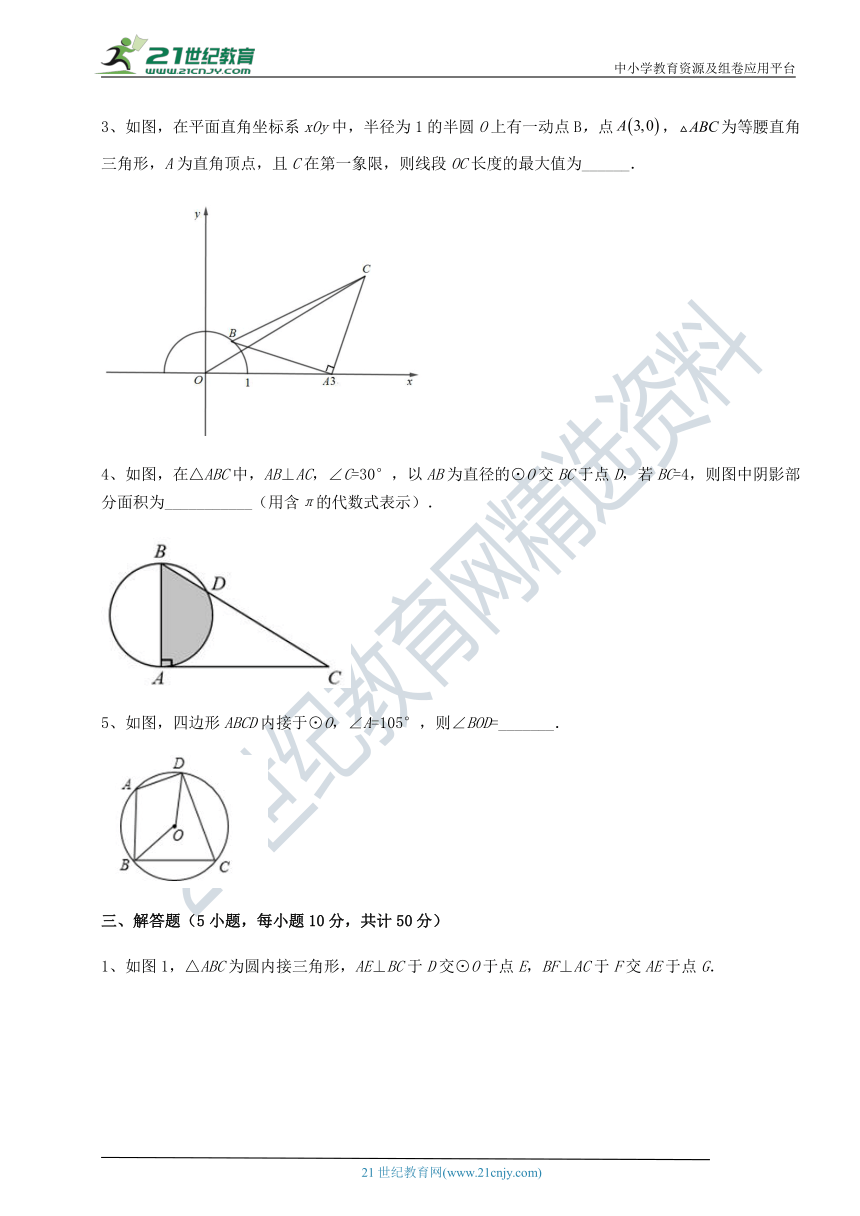
6、如图,在的网格中,A,B均为格点,以点A为圆心,AB的长为半径作弧,图中的点C是该弧与格线的交点,则的值是( )
( http: / / www.21cnjy.com / )
A. B. C. D.
7、如图,在中,,连接AC,CD,则AC与CD的关系是( ).
( http: / / www.21cnjy.com / )
A. B.
C. D.无法比较
8、如图,在圆内接五边形中,,则的度数为( )
( http: / / www.21cnjy.com / )
A. B. C. D.
9、如图,中,,,,点为的中点,以为圆心,长为半径作半圆,交于点,则图中阴影部分的面积是( )【版权所有:21教育】
( http: / / www.21cnjy.com / )
A. B. C. D.
10、如图,四边形ABCD内接于,若,则的度数为( )
( http: / / www.21cnjy.com / )
A.50° B.100° C.130° D.150°
第Ⅱ卷(非选择题 70分)
二、填空题(5小题,每小题4分,共计20分)
1、已知⊙O的直径为6cm,且点P在⊙O上,则线段PO=_________ .
2、如图,已知的半径为1,圆心在抛物线上运动,当与轴相切时,圆心的横坐标为______.21世纪教育网版权所有
( http: / / www.21cnjy.com / )
3、如图,在平面直角坐标系xOy中,半径为1的半圆O上有一动点B,点,为等腰直角三角形,A为直角顶点,且C在第一象限,则线段OC长度的最大值为______.
( http: / / www.21cnjy.com / )
4、如图,在△ABC中,AB⊥AC,∠C= ( http: / / www.21cnjy.com )30°,以AB为直径的⊙O交BC于点D,若BC=4,则图中阴影部分面积为___________(用含π的代数式表示).
( http: / / www.21cnjy.com / )
5、如图,四边形ABCD内接于⊙O,∠A=105°,则∠BOD=_______.
( http: / / www.21cnjy.com / )
三、解答题(5小题,每小题10分,共计50分)
1、如图1,△ABC为圆内接三角形,AE⊥BC于D交⊙O于点E,BF⊥AC于F交AE于点G.
( http: / / www.21cnjy.com / )
(1)求证:DG=DE;
(2)如图2,连接BE,作OM⊥BE于M,求证:AC=2OM;
(3)在(2)的条件下,连接OG、CE,若OG=CE,BG=2FC+2FG,AG=2,求OM长.
2、如图,A,P,B,C是⊙O上的四点,∠APC=∠CPB=60°.
(1)判断△ABC的形状,并证明你的结论;
(2)求证:PA+PB=PC.
( http: / / www.21cnjy.com / )
3、如图,以四边形的对角线为直径作圆,圆心为,点、在上,过点作的延长线于点,已知平分.21*cnjy*com
( http: / / www.21cnjy.com / )
(1)求证:是切线;
(2)若,,求的半径和的长.
4、如图,AB是⊙O的直径,弦CD⊥AB于点E,AM是△ACD的外角∠DAF的平分线.
( http: / / www.21cnjy.com / )
(1)求证:AM是⊙O的切线;
(2)连接CO并延长交AM于点N,若⊙O的半径为2,∠ANC = 30°,求CD的长.
5、如图,是的直径,弦,是的中点,连接并延长到点,使,连接交于点,连接,.
( http: / / www.21cnjy.com / )
(1)求证:直线是的切线;
(2)若长为,求的半径及的长.
-参考答案-
一、单选题
1、A
【分析】
根据圆周角定理得到∠ADB=90°,∠A=∠BCD=36°,然后利用互余计算∠ABD的度数.
【详解】
∵AB是⊙O的直径,
∴∠ADB=90°,
∵∠DAB=∠BCD=36°,
∴∠ABD=∠ADB﹣∠DAB,
即∠ABD=90°﹣∠DAB=90°﹣36°=54°.
故选:A.
【点睛】
本题考查了圆周角定理:在同圆或 ( http: / / www.21cnjy.com )等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.半圆(或直径)所对的圆周角是直角,90°的圆周角所对的弦是直径.
2、D
【分析】
先根据等边三角形的性质求出△OBC的面积,然后由地基的面积是△OBC的6倍即可得到答案
【详解】
解:如图所示,正六边形ABCDEF,连接OB,OC,过点O作OP⊥BC于P,
由题意得:BC=4cm,
∵六边形ABCD是正六边形,
∴∠BOC=360°÷6=60°,
又∵OB=OC,
∴△OBC是等边三角形,
∴,,
∴,
∴,
∴,
故选D.
( http: / / www.21cnjy.com / )
【点睛】
本题主要考查了正多边形和圆,等边三角形的性质与判定,勾股定理,熟知正多边形和圆的关系是解题的关键.
3、A
【分析】
首先由△ABC的外心即是三角形三边垂直平分线的交点,所以在平面直角坐标系中作AB与BC的垂线,两垂线的交点即为△ABC的外心.21·cn·jy·com
【详解】
解:∵△ABC的外心即是三角形三边垂直平分线的交点,
如图所示:EF与MN的交点O′即为所求的△ABC的外心,
∴△ABC的外心坐标是(﹣2,﹣1).
故选:A
( http: / / www.21cnjy.com / )
【点睛】
此题考查了三角形外心的知识.注意三角形的外心即是三角形三边垂直平分线的交点.解此题的关键是数形结合思想的应用.【来源:21·世纪·教育·网】
4、B
【分析】
连接OC,由垂径定理,得到CE=4,再由勾股定理求出OE的长度,即可求出AE的长度.
【详解】
解:连接OC,如图
( http: / / www.21cnjy.com / )
∵AB 为⊙O 的直径,CDAB,垂足为点 E,CD=8,
∴,
∵,
∴,
∴;
故选:B.
【点睛】
本题考查了垂径定理,勾股定理,解题的关键是掌握所学的知识,正确的求出.
5、B
【分析】
根据等腰三角形的性质,三线合一即可得,根据三角形切线的判定即可判断是的切线,进而可得⊙C 与AB的位置关系
【详解】
解:连接,
( http: / / www.21cnjy.com / )
,点O为AB中点.
CO为⊙C的半径,
是的切线,
⊙C 与AB的位置关系是相切
故选B
【点睛】
本题考查了三线合一,切线的判定,直线与圆的位置关系,掌握切线判定定理是解题的关键.
6、B
【分析】
利用,得到∠BAC=∠DCA,根据同圆的半径相等,AC=AB=3,再利用勾股定理求解 可得tan∠ACD=,从而可得答案.
【详解】
解:如图, ∵,
∴∠BAC=∠DCA.
( http: / / www.21cnjy.com / )
∵同圆的半径相等, ∴AC=AB=3,而
在Rt△ACD中,tan∠ACD=.
∴tan∠BAC=tan∠ACD=.
故选B.
【点睛】
本题主要考查了解直角三角形的应用,利用图形的性质进行角的等量代换是解本题的关键.
7、B
【分析】
连接AB,BC,根据得,再根据三角形三边关系可得结论.
【详解】
解:连接AB,BC,如图,
( http: / / www.21cnjy.com / )
∵
∴
又
∴
故选:B
【点睛】
本题考查了三角形三边关系,弧、弦的关系等知识,熟练掌握上述知识是解答本题的关键.
8、B
【分析】
先利用多边的内角和得到,可计算出,然后根据圆内接四边形的性质求出的度数即可.
【详解】
解:∵五边形的内角和为,
∴,
∵,
∴,
∵四边形为的内接四边形,
∴,
∴.
故选:B.
【点睛】
本题主要考查了多边形的内角和与圆内接四边形的性质,掌握圆内接四边形的性质是解答本题的关键.
9、A
【分析】
连接OD,BD,作OH⊥CD交CD于点H,首先根据勾股定理求出BC的长度,然后利用等面积法求出BD的长度,进而得到是等边三角形,,然后根据30°角直角三角形的性质求出OH的长度,最后根据进行计算即可.
【详解】
解:如图所示,连接OD,BD,作OH⊥CD交CD于点H
( http: / / www.21cnjy.com / )
∵,,
∴在中,
∵点为的中点,以为圆心,长为半径作半圆
∴是圆的直径,
∴
∴,即
解得:
又∵
∴
∴是等边三角形
∴
∴
∵OH⊥CD
∴,
∴.
故选:A.
【点睛】
本题考查了30°角直角三角形的性质, ( http: / / www.21cnjy.com )等边三角形的性质和判定,扇形面积,勾股定理等知识,正确添加辅助线,熟练掌握和灵活运用相关知识是解题的关键.
10、B
【分析】
根据圆内接四边形的性质求出∠A的度数,根据圆周角定理计算即可.
【详解】
解:∵四边形ABCD内接于⊙O,
∴∠A+∠DCB=180°,
∵∠DCB=130°,
∴∠A=50°,
由圆周角定理得,=2∠A=100°,
故选:B.
【点睛】
本题考查的是圆内接四边形的性质和圆周角定理,掌握圆内接四边形的对角互补是解题的关键.
二、填空题
1、3cm
【分析】
根据点与圆的位置关系得出:点P在⊙O上,则即可得出答案.
【详解】
∵⊙O的直径为6cm,
∴⊙O的半径为3cm,
∵点P在⊙O上,
∴.
故答案为:3cm.
【点睛】
本题考查点与圆的位置关系:点P在⊙O外,则,点P在⊙O上,则,点P在⊙O内,则.
2、2或或0
【分析】
当⊙P与x轴相切时,圆心P的纵坐标为1或-1,根据圆心P在抛物线上,所以当y为±1时,可以求出点P的横坐标.
【详解】
解:当y=1时,有1=-x2+1,x=0.
当y=-1时,有-1=-x2+1,x=.
故答案是:2或或0.
【点睛】
本题考查的是二次函数的综合题,利用圆与x轴相切得到点P的纵坐标,然后代入抛物线求出点P的横坐标.
3、1+
【分析】
过点C作CD⊥x轴于D,过B作BE⊥x轴于E,连结OB,设OD=x,根据点A(3,0)可求AD=x-3,根据为等腰直角三角形,得出AB=AC,∠BAC=90°,再证△BAE≌△ACD(AAS),得出BE=AD=x-3,EA=DC,在Rt△EBO中,根据勾股定理,
得出CD=AE=,根据勾股定理CO=,当OD=CD时OC最大,OC=此时解方程即可.
【详解】
解:过点C作CD⊥x轴于D,过B作BE⊥x轴于E,连结OB,设OD=x,
∵点A(3,0)
∴AD=x-3,
∵为等腰直角三角形,
∴AB=AC,∠BAC=90°,
∴∠BAE+∠CAD=180°-∠BAC=180°-90°=90°,
∵CD⊥x轴, BE⊥x轴,
∴∠BEA=∠ADC=90°,
∴∠ACD+∠CAD=90°,
∴∠ACD=∠BAE,
在△BAE和△ACD中,
,
∴△BAE≌△ACD(AAS),
∴BE=AD=x-3,EA=DC,
在Rt△EBO中,OB=1,BE= x-3,
根据勾股定理,
∴EA=OE+OA=,
∴CD=AE=,
∴CO=,
当OD=CD时OC最大,OC=,此时,
∴,
∴,
∴,
∴,(舍去),
∴线段OC长度的最大值为.
( http: / / www.21cnjy.com / )
故答案为:1+.
【点睛】
本题考查等腰直角三角形性质,三角形全等判定与性质,勾股定理,掌握等腰直角三角形性质,三角形全等判定与性质,勾股定理是解题关键.21教育网
4、
【分析】
连接,根据阴影部分面积为,根据等边三角形的面积,扇形面积公式进行计算即可
【详解】
解:如图,连接
( http: / / www.21cnjy.com / )
,,
,
AB为直径
是等边三角形
阴影部分面积为
故答案为:
【点睛】
本题考查了求扇形面积,添加辅助线将阴影部分面积转化为是解题的关键.
5、150°
【分析】
先根据圆内接四边形的性质求出∠C的度数,再由圆周角定理即可得出结论.
【详解】
∵四边形内接于,,
∴,
∴.
故答案为:.
【点睛】
本题考查的是圆内接四边形的性质,熟知圆内接四边形的对角互补是解答此题的关键.
三、解答题
1、(1)见解析;(2)见解析;(3).
【分析】
(1)连接BE,首先根据题意得到,然后根据同弧所对的圆周角相等得到,然后根据等角的余角相等得到,进而得到,最后根据等腰三角形三线合一性质即可证明出DG=DE;【来源:21cnj*y.co*m】
(2)连接AO,OB,OE,OC,作OH⊥AC于点H,首先根据圆周角定理以及角度之间的转化得到,然后证明,最后利用垂径定理即可证明AC=2OM;
(3)过点O作OH⊥AC于H,ON⊥BG于N,连接CG,OB,首先得到四边形ONFH是矩形,然后根据BG=2FC+2FG得出NG=CF,然后证明出△CDG≌△CDE(SAS)和△ONG≌△GFC(HL),设GF=ON=x,CF=GN=y,,根据勾股定理得到关于x和y的方程①,然后根据和得到关于x和y的方程②,联立方程①②即可求出OM的长度.
【详解】
解:(1)如图所示,连接BE,
( http: / / www.21cnjy.com / )
∵BF⊥AC,AE⊥BC
∴,
∴
∵
∴
∴
又∵
∴
∴
又∵AE⊥BC
∴DG=DE(三线合一);
(2)如图所示,连接AO,OB,OE,OC,作OH⊥AC于点H,
( http: / / www.21cnjy.com / )
∵OH⊥AC
∴,
∵,即
∴
∵
∴
∵
∴
∵
∴
又∵,
∴
∴
∴AC=2OM;
(3)如图所示,过点O作OH⊥AC于H,ON⊥BG于N,连接CG,OB,
( http: / / www.21cnjy.com / )
又∵
∴四边形ONFH是矩形,
∴NF=OH,
由(2)可知,
又∵BG=2FC+2FG,
∴,
∴ME=NF=FG+GN,
∴NG=CF,
∵在和中,
∴△CDG≌△CDE(SAS)
∴CE=CG=OG,
∵在和中,
∴△ONG≌△GFC(HL),
∴∠OGN=∠GCF,
∵
∴
∴∠OGC=90°,
∴是等腰直角三角形,
∴,
设GF=ON=x,CF=GN=y,则,,
在直角△ONG中,,则,
在直角△ONB中,,则,
∴,
∴①
∵,
∴
∵,
∴
∴,
在△AGF中,
∴,,
∵
∴,即,
∴,
∴
将①代入得:,
∴,
∴,即②,
联立①②解得,
∴,
∴
∴
【点睛】
此题考查了圆的综合题,勾股定理,全等 ( http: / / www.21cnjy.com )三角形的性质和判定,圆周角定理,三角函数等知识,解题的关键是熟练掌握以上知识点以及正确作出辅助线,根据题意列出方程求解.www.21-cn-jy.com
2、(1)△ABC是等边三角形,证明见解析;(2)见解析
【分析】
(1)利用圆周角定理可得 ( http: / / www.21cnjy.com )∠BAC=∠CPB,∠ABC=∠APC,而∠APC=∠CPB=60°,所以∠BAC=∠ABC=60°,从而可判断△ABC的形状;【出处:21教育名师】
(2)如图所示,在PC取一点E使得AE=A ( http: / / www.21cnjy.com )P,先证明△APE是等边三角形,得到AP=PE,∠AEP=60°,可以推出∠AEC=∠APB,然后证明△APB≌△AEC得到BP=CE,即可证明PC=PE+CE=AP+BP.
【详解】
解:(1)△ABC是等边三角形.证明如下:
由圆周角定理:∠BAC=∠CPB,∠ABC=∠APC
∵∠APC=∠CPB=60°,
∴∠BAC=∠ABC=60°,
∴∠ACB=180°-∠BAC-∠ABC=180°-60°-60°=60°.
∴△ABC是等边三角形.
(2)如图所示,在PC取一点E使得AE=AP,
∵∠APE=60°,AP=AE,
∴△APE是等边三角形,
∴AP=PE,∠AEP=60°,
∴∠AEC=120°,
又∵∠APC=∠CPB=60°,
∴∠APB=120°,
∴∠AEC=∠APB,
∵△ABC是等边三角形,
∴AB=AC,
又∵∠ABP=∠ACE,
∴△APB≌△AEC(AAS),
∴BP=CE,
∴PC=PE+CE=AP+BP.
( http: / / www.21cnjy.com / )
【点睛】
本题考查了圆周角定理、等边三角形的性质与判定,全等三角形的性质与判定,解题的关键是掌握圆周角定理,正确求出∠ABC=∠BAC=60°.
3、
(1)证明见解析
(2)
【分析】
(1)连接OA,根据已知条件证明OA⊥AE即可解决问题;
(2)取CD中点F,连接OF,根据垂径定理可得OF⊥CD,所以四边形AEFO是矩形,利用勾股定理即可求出结果.
(1)
证明:如图,连接OA,
∵AE⊥CD,
∴∠DAE+∠ADE=90°.
∵DA平分∠BDE,
∴∠ADE=∠ADO,
又∵OA=OD,
∴∠OAD=∠ADO,
∴∠DAE+∠OAD=90°,
∴OA⊥AE,
∴AE是⊙O切线;
( http: / / www.21cnjy.com / )(2)
解:如图,取CD中点F,连接OF,
∴OF⊥CD于点F.
∴四边形AEFO是矩形,
∵CD=6,
∴DF=FC=3.
在Rt△OFD中,OF=AE=4,
∴,
在Rt△AED中,AE=4,ED=EF-DF=OA-DF=OD-DF=5-3=2,
∴,
∴AD的长是.
【点睛】
本题考查了切线的判定与性质,垂径定理,圆周角定理,勾股定理,解决本题的关键是掌握切线的判定与性质.
4、
(1)见解析
(2)CD=2
【分析】
(1)由题意易得BC=BD,∠DAM=∠DAF,则有∠CAB=∠DAB,进而可得∠BAM=90°,然后问题可求证;
(2)由题意易得CD//AM,∠ANC=∠OCE=30°,然后可得OE=1,CE=,进而问题可求解.
(1)
证明:∵AB是⊙O的直径,弦CD⊥AB于点E
∴BC=BD
∴∠CAB=∠DAB
∵AM是∠DAF的平分线
∴∠DAM=∠DAF
∵∠CAD+∠DAF=180°
∴∠DAB+∠DAM=90°
即∠BAM=90°,AB⊥AM
∴AM是⊙O的切线
(2)
解:∵AB⊥CD,AB⊥AM
∴CD//AM
∴∠ANC=∠OCE=30°
在Rt△OCE中,OC=2
∴OE=1,CE=
∵AB是⊙O的直径,弦CD⊥AB于点E
∴CD=2CE=2.
【点睛】
本题主要考查切线的判定定理、垂径定理及含30度直角三角形的性质,熟练掌握切线的判定定理、垂径定理及含30度直角三角形的性质是解题的关键.21cnjy.com
5、(1)见解析;(2)的半径为,.
【分析】
(1)如图:连OC,根据、得CO⊥AB,进而证明即可得到∠FBE=∠COE=90°,即可证明直线是⊙的切线;21·世纪*教育网
(2)由设的半径为,则,,在Rt ABF运用勾股定理即可得半径r,然后再求得AB,最后运用等面积法求解即可.21*cnjy*com
【详解】
(1)如图:连接
∵、
∴
∵,,,
∴
∴
∴
又∵经过半径的外端点
∴是的切线;
(2)设的半径为,则,
在中有:
∴只取,即的半径为.
∵是的直径、即,
∴
∴,
∵AB为直径,
∴∠ADB=90°,
∴,
∴,解得.
( http: / / www.21cnjy.com / )
【点睛】
本题主要考查了切线的判定和性质、全等三角形的判定和性质、勾股定理、圆周角定理等知识点,正确的作出辅助线是解答本题的关键.2·1·c·n·j·y
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
九年级数学第二学期第二十七章圆与正多边形章节练习
考试时间:90分钟;命题人:数学教研组
考生注意:
1、本卷分第I卷(选择题)和第Ⅱ卷(非选择题)两部分,满分100分,考试时间90分钟
2、答卷前,考生务必用0.5毫米黑色签字笔将自己的姓名、班级填写在试卷规定位置上
3、答案必须写在试卷各个题 ( http: / / www.21cnjy.com )目指定区域内相应的位置,如需改动,先划掉原来的答案,然后再写上新的答案;不准使用涂改液、胶带纸、修正带,不按以上要求作答的答案无效。www-2-1-cnjy-com
第I卷(选择题 30分)
一、单选题(10小题,每小题3分,共计30分)
1、如图,已知AB是⊙O的直径,CD是弦,若∠BCD=36°,则∠ABD等于( )
( http: / / www.21cnjy.com / )
A.54° B.56° C.64° D.66°
2、如图,有一个亭子,它的地基是边长为4m的正六边形,则地基的面积为( )
( http: / / www.21cnjy.com / )
A.4m2 B.12m2 C.24m2 D.24m2
3、如图,在平面直角坐标系xOy中,点A ( http: / / www.21cnjy.com )(0,3),点B(2,1),点C(2,-3).则经画图操作可知:△ABC的外接圆的圆心坐标是( )2-1-c-n-j-y
( http: / / www.21cnjy.com / )
A.(-2,-1) B.(-1,0) C.(-1,-1) D.(0,-1)
4、如图,AB 为⊙O 的直径,弦 CDAB,垂足为点 E,若 ⊙O的半径为5,CD=8,则AE的长为( )
( http: / / www.21cnjy.com / )
A.3 B.2 C.1 D.
5、在△ABC中,,点O为AB中点.以点C为圆心,CO长为半径作⊙C,则⊙C 与AB的位置关系是( )21教育名师原创作品
( http: / / www.21cnjy.com / )
A.相交 B.相切
C.相离 D.不确定
6、如图,在的网格中,A,B均为格点,以点A为圆心,AB的长为半径作弧,图中的点C是该弧与格线的交点,则的值是( )
( http: / / www.21cnjy.com / )
A. B. C. D.
7、如图,在中,,连接AC,CD,则AC与CD的关系是( ).
( http: / / www.21cnjy.com / )
A. B.
C. D.无法比较
8、如图,在圆内接五边形中,,则的度数为( )
( http: / / www.21cnjy.com / )
A. B. C. D.
9、如图,中,,,,点为的中点,以为圆心,长为半径作半圆,交于点,则图中阴影部分的面积是( )【版权所有:21教育】
( http: / / www.21cnjy.com / )
A. B. C. D.
10、如图,四边形ABCD内接于,若,则的度数为( )
( http: / / www.21cnjy.com / )
A.50° B.100° C.130° D.150°
第Ⅱ卷(非选择题 70分)
二、填空题(5小题,每小题4分,共计20分)
1、已知⊙O的直径为6cm,且点P在⊙O上,则线段PO=_________ .
2、如图,已知的半径为1,圆心在抛物线上运动,当与轴相切时,圆心的横坐标为______.21世纪教育网版权所有
( http: / / www.21cnjy.com / )
3、如图,在平面直角坐标系xOy中,半径为1的半圆O上有一动点B,点,为等腰直角三角形,A为直角顶点,且C在第一象限,则线段OC长度的最大值为______.
( http: / / www.21cnjy.com / )
4、如图,在△ABC中,AB⊥AC,∠C= ( http: / / www.21cnjy.com )30°,以AB为直径的⊙O交BC于点D,若BC=4,则图中阴影部分面积为___________(用含π的代数式表示).
( http: / / www.21cnjy.com / )
5、如图,四边形ABCD内接于⊙O,∠A=105°,则∠BOD=_______.
( http: / / www.21cnjy.com / )
三、解答题(5小题,每小题10分,共计50分)
1、如图1,△ABC为圆内接三角形,AE⊥BC于D交⊙O于点E,BF⊥AC于F交AE于点G.
( http: / / www.21cnjy.com / )
(1)求证:DG=DE;
(2)如图2,连接BE,作OM⊥BE于M,求证:AC=2OM;
(3)在(2)的条件下,连接OG、CE,若OG=CE,BG=2FC+2FG,AG=2,求OM长.
2、如图,A,P,B,C是⊙O上的四点,∠APC=∠CPB=60°.
(1)判断△ABC的形状,并证明你的结论;
(2)求证:PA+PB=PC.
( http: / / www.21cnjy.com / )
3、如图,以四边形的对角线为直径作圆,圆心为,点、在上,过点作的延长线于点,已知平分.21*cnjy*com
( http: / / www.21cnjy.com / )
(1)求证:是切线;
(2)若,,求的半径和的长.
4、如图,AB是⊙O的直径,弦CD⊥AB于点E,AM是△ACD的外角∠DAF的平分线.
( http: / / www.21cnjy.com / )
(1)求证:AM是⊙O的切线;
(2)连接CO并延长交AM于点N,若⊙O的半径为2,∠ANC = 30°,求CD的长.
5、如图,是的直径,弦,是的中点,连接并延长到点,使,连接交于点,连接,.
( http: / / www.21cnjy.com / )
(1)求证:直线是的切线;
(2)若长为,求的半径及的长.
-参考答案-
一、单选题
1、A
【分析】
根据圆周角定理得到∠ADB=90°,∠A=∠BCD=36°,然后利用互余计算∠ABD的度数.
【详解】
∵AB是⊙O的直径,
∴∠ADB=90°,
∵∠DAB=∠BCD=36°,
∴∠ABD=∠ADB﹣∠DAB,
即∠ABD=90°﹣∠DAB=90°﹣36°=54°.
故选:A.
【点睛】
本题考查了圆周角定理:在同圆或 ( http: / / www.21cnjy.com )等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.半圆(或直径)所对的圆周角是直角,90°的圆周角所对的弦是直径.
2、D
【分析】
先根据等边三角形的性质求出△OBC的面积,然后由地基的面积是△OBC的6倍即可得到答案
【详解】
解:如图所示,正六边形ABCDEF,连接OB,OC,过点O作OP⊥BC于P,
由题意得:BC=4cm,
∵六边形ABCD是正六边形,
∴∠BOC=360°÷6=60°,
又∵OB=OC,
∴△OBC是等边三角形,
∴,,
∴,
∴,
∴,
故选D.
( http: / / www.21cnjy.com / )
【点睛】
本题主要考查了正多边形和圆,等边三角形的性质与判定,勾股定理,熟知正多边形和圆的关系是解题的关键.
3、A
【分析】
首先由△ABC的外心即是三角形三边垂直平分线的交点,所以在平面直角坐标系中作AB与BC的垂线,两垂线的交点即为△ABC的外心.21·cn·jy·com
【详解】
解:∵△ABC的外心即是三角形三边垂直平分线的交点,
如图所示:EF与MN的交点O′即为所求的△ABC的外心,
∴△ABC的外心坐标是(﹣2,﹣1).
故选:A
( http: / / www.21cnjy.com / )
【点睛】
此题考查了三角形外心的知识.注意三角形的外心即是三角形三边垂直平分线的交点.解此题的关键是数形结合思想的应用.【来源:21·世纪·教育·网】
4、B
【分析】
连接OC,由垂径定理,得到CE=4,再由勾股定理求出OE的长度,即可求出AE的长度.
【详解】
解:连接OC,如图
( http: / / www.21cnjy.com / )
∵AB 为⊙O 的直径,CDAB,垂足为点 E,CD=8,
∴,
∵,
∴,
∴;
故选:B.
【点睛】
本题考查了垂径定理,勾股定理,解题的关键是掌握所学的知识,正确的求出.
5、B
【分析】
根据等腰三角形的性质,三线合一即可得,根据三角形切线的判定即可判断是的切线,进而可得⊙C 与AB的位置关系
【详解】
解:连接,
( http: / / www.21cnjy.com / )
,点O为AB中点.
CO为⊙C的半径,
是的切线,
⊙C 与AB的位置关系是相切
故选B
【点睛】
本题考查了三线合一,切线的判定,直线与圆的位置关系,掌握切线判定定理是解题的关键.
6、B
【分析】
利用,得到∠BAC=∠DCA,根据同圆的半径相等,AC=AB=3,再利用勾股定理求解 可得tan∠ACD=,从而可得答案.
【详解】
解:如图, ∵,
∴∠BAC=∠DCA.
( http: / / www.21cnjy.com / )
∵同圆的半径相等, ∴AC=AB=3,而
在Rt△ACD中,tan∠ACD=.
∴tan∠BAC=tan∠ACD=.
故选B.
【点睛】
本题主要考查了解直角三角形的应用,利用图形的性质进行角的等量代换是解本题的关键.
7、B
【分析】
连接AB,BC,根据得,再根据三角形三边关系可得结论.
【详解】
解:连接AB,BC,如图,
( http: / / www.21cnjy.com / )
∵
∴
又
∴
故选:B
【点睛】
本题考查了三角形三边关系,弧、弦的关系等知识,熟练掌握上述知识是解答本题的关键.
8、B
【分析】
先利用多边的内角和得到,可计算出,然后根据圆内接四边形的性质求出的度数即可.
【详解】
解:∵五边形的内角和为,
∴,
∵,
∴,
∵四边形为的内接四边形,
∴,
∴.
故选:B.
【点睛】
本题主要考查了多边形的内角和与圆内接四边形的性质,掌握圆内接四边形的性质是解答本题的关键.
9、A
【分析】
连接OD,BD,作OH⊥CD交CD于点H,首先根据勾股定理求出BC的长度,然后利用等面积法求出BD的长度,进而得到是等边三角形,,然后根据30°角直角三角形的性质求出OH的长度,最后根据进行计算即可.
【详解】
解:如图所示,连接OD,BD,作OH⊥CD交CD于点H
( http: / / www.21cnjy.com / )
∵,,
∴在中,
∵点为的中点,以为圆心,长为半径作半圆
∴是圆的直径,
∴
∴,即
解得:
又∵
∴
∴是等边三角形
∴
∴
∵OH⊥CD
∴,
∴.
故选:A.
【点睛】
本题考查了30°角直角三角形的性质, ( http: / / www.21cnjy.com )等边三角形的性质和判定,扇形面积,勾股定理等知识,正确添加辅助线,熟练掌握和灵活运用相关知识是解题的关键.
10、B
【分析】
根据圆内接四边形的性质求出∠A的度数,根据圆周角定理计算即可.
【详解】
解:∵四边形ABCD内接于⊙O,
∴∠A+∠DCB=180°,
∵∠DCB=130°,
∴∠A=50°,
由圆周角定理得,=2∠A=100°,
故选:B.
【点睛】
本题考查的是圆内接四边形的性质和圆周角定理,掌握圆内接四边形的对角互补是解题的关键.
二、填空题
1、3cm
【分析】
根据点与圆的位置关系得出:点P在⊙O上,则即可得出答案.
【详解】
∵⊙O的直径为6cm,
∴⊙O的半径为3cm,
∵点P在⊙O上,
∴.
故答案为:3cm.
【点睛】
本题考查点与圆的位置关系:点P在⊙O外,则,点P在⊙O上,则,点P在⊙O内,则.
2、2或或0
【分析】
当⊙P与x轴相切时,圆心P的纵坐标为1或-1,根据圆心P在抛物线上,所以当y为±1时,可以求出点P的横坐标.
【详解】
解:当y=1时,有1=-x2+1,x=0.
当y=-1时,有-1=-x2+1,x=.
故答案是:2或或0.
【点睛】
本题考查的是二次函数的综合题,利用圆与x轴相切得到点P的纵坐标,然后代入抛物线求出点P的横坐标.
3、1+
【分析】
过点C作CD⊥x轴于D,过B作BE⊥x轴于E,连结OB,设OD=x,根据点A(3,0)可求AD=x-3,根据为等腰直角三角形,得出AB=AC,∠BAC=90°,再证△BAE≌△ACD(AAS),得出BE=AD=x-3,EA=DC,在Rt△EBO中,根据勾股定理,
得出CD=AE=,根据勾股定理CO=,当OD=CD时OC最大,OC=此时解方程即可.
【详解】
解:过点C作CD⊥x轴于D,过B作BE⊥x轴于E,连结OB,设OD=x,
∵点A(3,0)
∴AD=x-3,
∵为等腰直角三角形,
∴AB=AC,∠BAC=90°,
∴∠BAE+∠CAD=180°-∠BAC=180°-90°=90°,
∵CD⊥x轴, BE⊥x轴,
∴∠BEA=∠ADC=90°,
∴∠ACD+∠CAD=90°,
∴∠ACD=∠BAE,
在△BAE和△ACD中,
,
∴△BAE≌△ACD(AAS),
∴BE=AD=x-3,EA=DC,
在Rt△EBO中,OB=1,BE= x-3,
根据勾股定理,
∴EA=OE+OA=,
∴CD=AE=,
∴CO=,
当OD=CD时OC最大,OC=,此时,
∴,
∴,
∴,
∴,(舍去),
∴线段OC长度的最大值为.
( http: / / www.21cnjy.com / )
故答案为:1+.
【点睛】
本题考查等腰直角三角形性质,三角形全等判定与性质,勾股定理,掌握等腰直角三角形性质,三角形全等判定与性质,勾股定理是解题关键.21教育网
4、
【分析】
连接,根据阴影部分面积为,根据等边三角形的面积,扇形面积公式进行计算即可
【详解】
解:如图,连接
( http: / / www.21cnjy.com / )
,,
,
AB为直径
是等边三角形
阴影部分面积为
故答案为:
【点睛】
本题考查了求扇形面积,添加辅助线将阴影部分面积转化为是解题的关键.
5、150°
【分析】
先根据圆内接四边形的性质求出∠C的度数,再由圆周角定理即可得出结论.
【详解】
∵四边形内接于,,
∴,
∴.
故答案为:.
【点睛】
本题考查的是圆内接四边形的性质,熟知圆内接四边形的对角互补是解答此题的关键.
三、解答题
1、(1)见解析;(2)见解析;(3).
【分析】
(1)连接BE,首先根据题意得到,然后根据同弧所对的圆周角相等得到,然后根据等角的余角相等得到,进而得到,最后根据等腰三角形三线合一性质即可证明出DG=DE;【来源:21cnj*y.co*m】
(2)连接AO,OB,OE,OC,作OH⊥AC于点H,首先根据圆周角定理以及角度之间的转化得到,然后证明,最后利用垂径定理即可证明AC=2OM;
(3)过点O作OH⊥AC于H,ON⊥BG于N,连接CG,OB,首先得到四边形ONFH是矩形,然后根据BG=2FC+2FG得出NG=CF,然后证明出△CDG≌△CDE(SAS)和△ONG≌△GFC(HL),设GF=ON=x,CF=GN=y,,根据勾股定理得到关于x和y的方程①,然后根据和得到关于x和y的方程②,联立方程①②即可求出OM的长度.
【详解】
解:(1)如图所示,连接BE,
( http: / / www.21cnjy.com / )
∵BF⊥AC,AE⊥BC
∴,
∴
∵
∴
∴
又∵
∴
∴
又∵AE⊥BC
∴DG=DE(三线合一);
(2)如图所示,连接AO,OB,OE,OC,作OH⊥AC于点H,
( http: / / www.21cnjy.com / )
∵OH⊥AC
∴,
∵,即
∴
∵
∴
∵
∴
∵
∴
又∵,
∴
∴
∴AC=2OM;
(3)如图所示,过点O作OH⊥AC于H,ON⊥BG于N,连接CG,OB,
( http: / / www.21cnjy.com / )
又∵
∴四边形ONFH是矩形,
∴NF=OH,
由(2)可知,
又∵BG=2FC+2FG,
∴,
∴ME=NF=FG+GN,
∴NG=CF,
∵在和中,
∴△CDG≌△CDE(SAS)
∴CE=CG=OG,
∵在和中,
∴△ONG≌△GFC(HL),
∴∠OGN=∠GCF,
∵
∴
∴∠OGC=90°,
∴是等腰直角三角形,
∴,
设GF=ON=x,CF=GN=y,则,,
在直角△ONG中,,则,
在直角△ONB中,,则,
∴,
∴①
∵,
∴
∵,
∴
∴,
在△AGF中,
∴,,
∵
∴,即,
∴,
∴
将①代入得:,
∴,
∴,即②,
联立①②解得,
∴,
∴
∴
【点睛】
此题考查了圆的综合题,勾股定理,全等 ( http: / / www.21cnjy.com )三角形的性质和判定,圆周角定理,三角函数等知识,解题的关键是熟练掌握以上知识点以及正确作出辅助线,根据题意列出方程求解.www.21-cn-jy.com
2、(1)△ABC是等边三角形,证明见解析;(2)见解析
【分析】
(1)利用圆周角定理可得 ( http: / / www.21cnjy.com )∠BAC=∠CPB,∠ABC=∠APC,而∠APC=∠CPB=60°,所以∠BAC=∠ABC=60°,从而可判断△ABC的形状;【出处:21教育名师】
(2)如图所示,在PC取一点E使得AE=A ( http: / / www.21cnjy.com )P,先证明△APE是等边三角形,得到AP=PE,∠AEP=60°,可以推出∠AEC=∠APB,然后证明△APB≌△AEC得到BP=CE,即可证明PC=PE+CE=AP+BP.
【详解】
解:(1)△ABC是等边三角形.证明如下:
由圆周角定理:∠BAC=∠CPB,∠ABC=∠APC
∵∠APC=∠CPB=60°,
∴∠BAC=∠ABC=60°,
∴∠ACB=180°-∠BAC-∠ABC=180°-60°-60°=60°.
∴△ABC是等边三角形.
(2)如图所示,在PC取一点E使得AE=AP,
∵∠APE=60°,AP=AE,
∴△APE是等边三角形,
∴AP=PE,∠AEP=60°,
∴∠AEC=120°,
又∵∠APC=∠CPB=60°,
∴∠APB=120°,
∴∠AEC=∠APB,
∵△ABC是等边三角形,
∴AB=AC,
又∵∠ABP=∠ACE,
∴△APB≌△AEC(AAS),
∴BP=CE,
∴PC=PE+CE=AP+BP.
( http: / / www.21cnjy.com / )
【点睛】
本题考查了圆周角定理、等边三角形的性质与判定,全等三角形的性质与判定,解题的关键是掌握圆周角定理,正确求出∠ABC=∠BAC=60°.
3、
(1)证明见解析
(2)
【分析】
(1)连接OA,根据已知条件证明OA⊥AE即可解决问题;
(2)取CD中点F,连接OF,根据垂径定理可得OF⊥CD,所以四边形AEFO是矩形,利用勾股定理即可求出结果.
(1)
证明:如图,连接OA,
∵AE⊥CD,
∴∠DAE+∠ADE=90°.
∵DA平分∠BDE,
∴∠ADE=∠ADO,
又∵OA=OD,
∴∠OAD=∠ADO,
∴∠DAE+∠OAD=90°,
∴OA⊥AE,
∴AE是⊙O切线;
( http: / / www.21cnjy.com / )(2)
解:如图,取CD中点F,连接OF,
∴OF⊥CD于点F.
∴四边形AEFO是矩形,
∵CD=6,
∴DF=FC=3.
在Rt△OFD中,OF=AE=4,
∴,
在Rt△AED中,AE=4,ED=EF-DF=OA-DF=OD-DF=5-3=2,
∴,
∴AD的长是.
【点睛】
本题考查了切线的判定与性质,垂径定理,圆周角定理,勾股定理,解决本题的关键是掌握切线的判定与性质.
4、
(1)见解析
(2)CD=2
【分析】
(1)由题意易得BC=BD,∠DAM=∠DAF,则有∠CAB=∠DAB,进而可得∠BAM=90°,然后问题可求证;
(2)由题意易得CD//AM,∠ANC=∠OCE=30°,然后可得OE=1,CE=,进而问题可求解.
(1)
证明:∵AB是⊙O的直径,弦CD⊥AB于点E
∴BC=BD
∴∠CAB=∠DAB
∵AM是∠DAF的平分线
∴∠DAM=∠DAF
∵∠CAD+∠DAF=180°
∴∠DAB+∠DAM=90°
即∠BAM=90°,AB⊥AM
∴AM是⊙O的切线
(2)
解:∵AB⊥CD,AB⊥AM
∴CD//AM
∴∠ANC=∠OCE=30°
在Rt△OCE中,OC=2
∴OE=1,CE=
∵AB是⊙O的直径,弦CD⊥AB于点E
∴CD=2CE=2.
【点睛】
本题主要考查切线的判定定理、垂径定理及含30度直角三角形的性质,熟练掌握切线的判定定理、垂径定理及含30度直角三角形的性质是解题的关键.21cnjy.com
5、(1)见解析;(2)的半径为,.
【分析】
(1)如图:连OC,根据、得CO⊥AB,进而证明即可得到∠FBE=∠COE=90°,即可证明直线是⊙的切线;21·世纪*教育网
(2)由设的半径为,则,,在Rt ABF运用勾股定理即可得半径r,然后再求得AB,最后运用等面积法求解即可.21*cnjy*com
【详解】
(1)如图:连接
∵、
∴
∵,,,
∴
∴
∴
又∵经过半径的外端点
∴是的切线;
(2)设的半径为,则,
在中有:
∴只取,即的半径为.
∵是的直径、即,
∴
∴,
∵AB为直径,
∴∠ADB=90°,
∴,
∴,解得.
( http: / / www.21cnjy.com / )
【点睛】
本题主要考查了切线的判定和性质、全等三角形的判定和性质、勾股定理、圆周角定理等知识点,正确的作出辅助线是解答本题的关键.2·1·c·n·j·y
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
