【强化训练】沪教版(上海)九下 第二十七章圆与正多边形综合测评试题(含解析)
文档属性
| 名称 | 【强化训练】沪教版(上海)九下 第二十七章圆与正多边形综合测评试题(含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 2.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-22 08:53:56 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
九年级数学第二学期第二十七章圆与正多边形综合测评
考试时间:90分钟;命题人:数学教研组
考生注意:
1、本卷分第I卷(选择题)和第Ⅱ卷(非选择题)两部分,满分100分,考试时间90分钟
2、答卷前,考生务必用0.5毫米黑色签字笔将自己的姓名、班级填写在试卷规定位置上
3、答案必须写在试卷各个题目指定区域内 ( http: / / www.21cnjy.com )相应的位置,如需改动,先划掉原来的答案,然后再写上新的答案;不准使用涂改液、胶带纸、修正带,不按以上要求作答的答案无效。www.21-cn-jy.com
第I卷(选择题 30分)
一、单选题(10小题,每小题3分,共计30分)
1、如图,Rt△ABC中,∠A=90°,∠B ( http: / / www.21cnjy.com )=30°,AC=1,将Rt△ABC延直线l由图1的位置按顺时针方向向右作无滑动滚动,当A第一次滚动到图2位置时,顶点A所经过的路径的长为( )
( http: / / www.21cnjy.com / )
A. B. C. D.(2+)π
2、如图,已知AB是⊙O的直径,CD是弦,若∠BCD=36°,则∠ABD等于( )
( http: / / www.21cnjy.com / )
A.54° B.56° C.64° D.66°
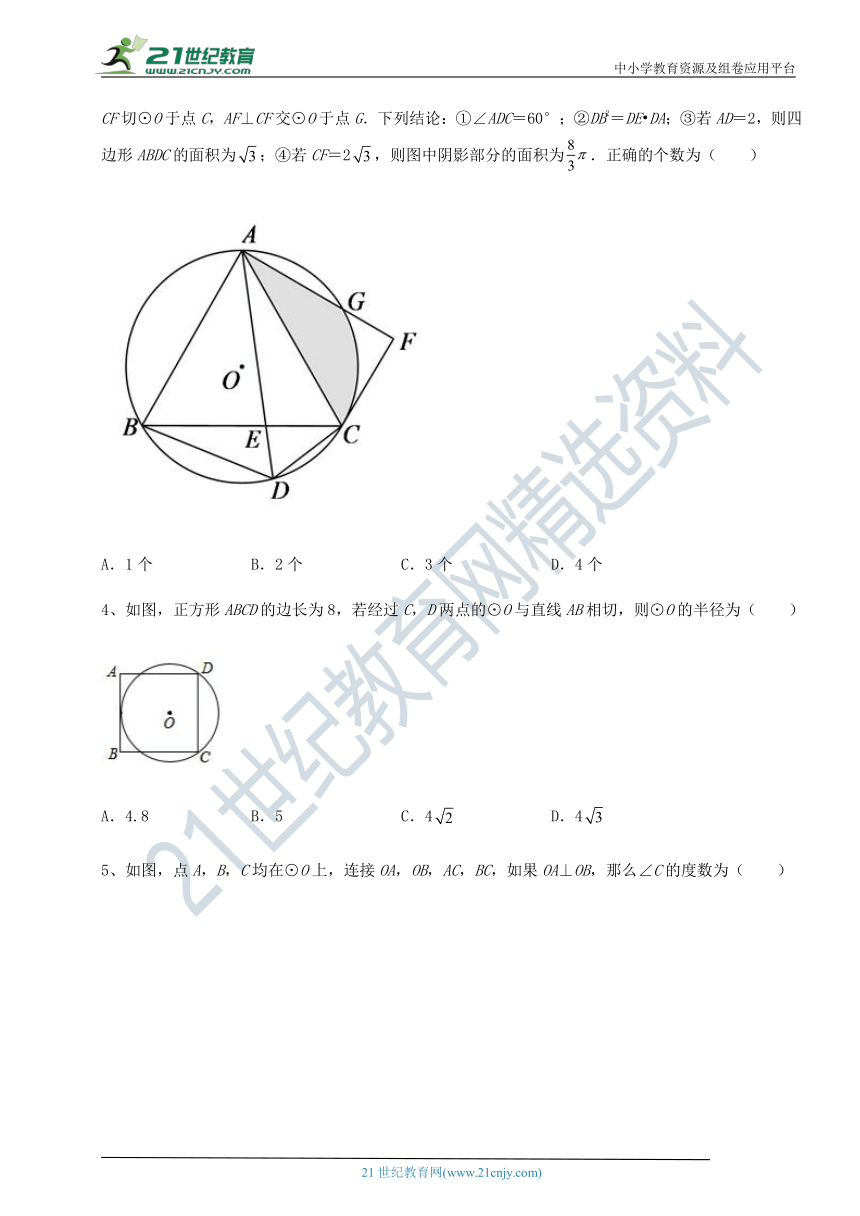
3、如图,等边△ABC内接于⊙O,D是上任一点(不与B、C重合),连接BD、CD,AD交BC于E,CF切⊙O于点C,AF⊥CF交⊙O于点G.下列结论:①∠ADC=60°;②DB2=DE DA;③若AD=2,则四边形ABDC的面积为;④若CF=2,则图中阴影部分的面积为.正确的个数为( )
( http: / / www.21cnjy.com / )
A.1个 B.2个 C.3个 D.4个
4、如图,正方形ABCD的边长为8,若经过C,D两点的⊙O与直线AB相切,则⊙O的半径为( )
( http: / / www.21cnjy.com / )
A.4.8 B.5 C.4 D.4
5、如图,点A,B,C均在⊙O上,连接OA,OB,AC,BC,如果OA⊥OB,那么∠C的度数为( )
( http: / / www.21cnjy.com / )
A.22.5° B.45° C.90° D.67.5°
6、如图,AB是⊙O的直径,BD与⊙O相切于 ( http: / / www.21cnjy.com )点B,点C是⊙O上一点,连接AC并延长,交BD于点D,连接OC,BC,若∠BOC=50°,则∠D的度数为( )【来源:21cnj*y.co*m】
( http: / / www.21cnjy.com / )
A.50° B.55° C.65° D.75°
7、如图,在圆内接五边形中,,则的度数为( )
( http: / / www.21cnjy.com / )
A. B. C. D.
8、在平面直角坐标系xOy中,已知点A(﹣4,﹣3),以点A为圆心,4为半径画⊙A,则坐标原点O与⊙A的位置关系是( )
A.点O在⊙A内 B.点O在⊙A外
C.点O在⊙A上 D.以上都有可能
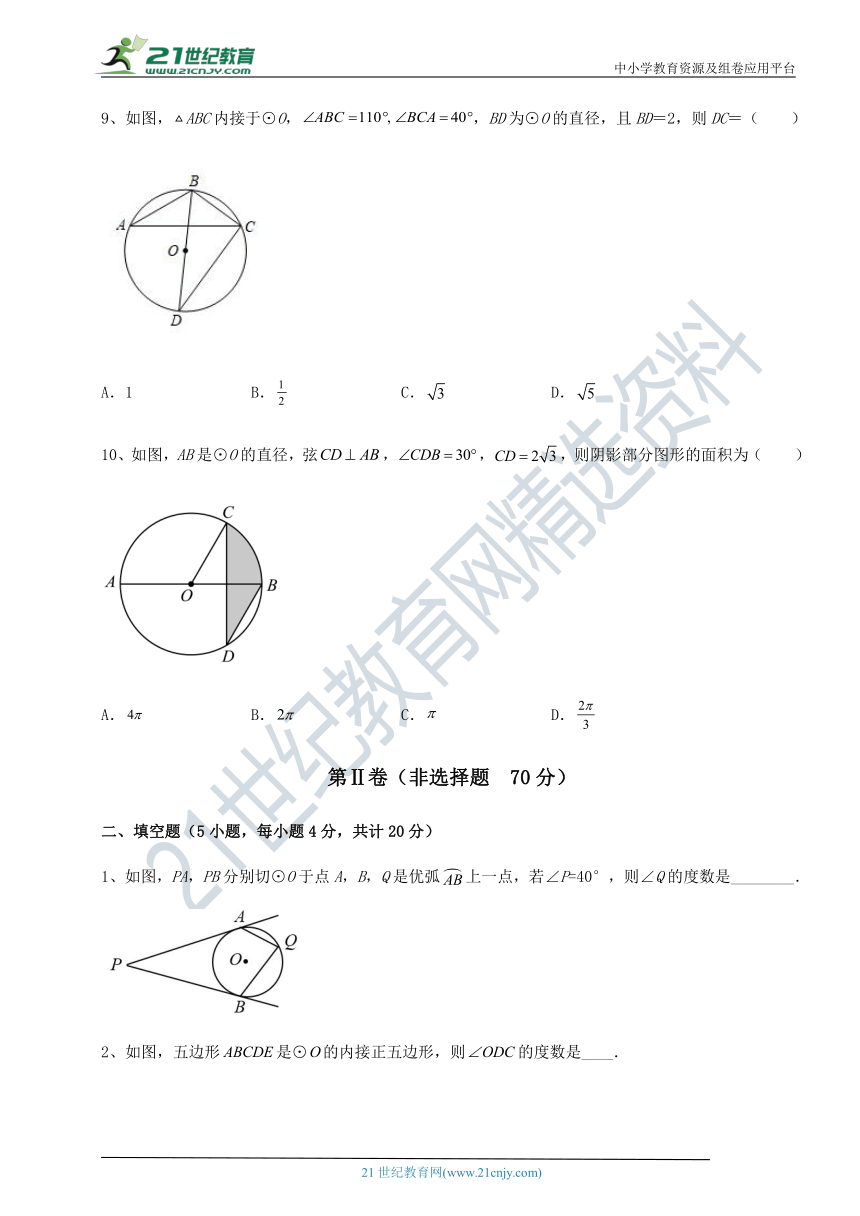
9、如图,ABC内接于⊙O,,BD为⊙O的直径,且BD=2,则DC=( )
( http: / / www.21cnjy.com / )
A.1 B. C. D.
10、如图,AB是⊙O的直径,弦,,,则阴影部分图形的面积为( )
( http: / / www.21cnjy.com / )
A. B. C. D.
第Ⅱ卷(非选择题 70分)
二、填空题(5小题,每小题4分,共计20分)
1、如图,PA,PB分别切⊙O于点A,B,Q是优弧上一点,若∠P=40°,则∠Q的度数是________.
( http: / / www.21cnjy.com / )
2、如图,五边形是⊙的内接正五边形,则的度数是____.
( http: / / www.21cnjy.com / )
3、如图AB为⊙O的直径 ( http: / / www.21cnjy.com ),点P为AB延长线上的点,过点P作⊙O的切线PE,切点为M,过A、B两点分别作PE垂线AC、BD,垂足分别为C、D,连接AM,则下列结论正确的是______(写所有正确论的号)
①AM平分∠CAB;②;③若AB=4,∠APE=30°,则的长为;④若AC=3BD,则有tan∠MAP=.
( http: / / www.21cnjy.com / )
4、已知O、I分别是△ABC的外心和内心,∠BIC=125°,则∠BOC的大小是 ___度.
5、圆形角是270°的扇形的半径为4cm,则这个扇形的面积是______.
三、解答题(5小题,每小题10分,共计50分)
1、如图,PA,PB与⊙O ( http: / / www.21cnjy.com )相切,切点为A,B,CD与⊙O相切于点E,分别交PA,PB于点D,C.若PA,PB的长是关于x的一元二次方程x2﹣mx+m﹣1=0的两个根.
(1)求m的值;
(2)求△PCD的周长.
( http: / / www.21cnjy.com / )
2、已知:如图,射线.
求作:,使得点在射线上,,.
作法:①在射线上任取一点;
②以点为圆心,的长为半径画圆,交射线于另一点;
③以点为圆心,的长为半径画弧,在射线上方交于点;
④连接、.
(1)使用直尺和圆规,依作法补全图形(保留作图痕迹);
(2)完成下面的证明.
证明:为的直径,点在上,
(___________________________)(填推理依据).
连接.
,
为等边三角形(___________________________)(填推理依据).
所以为所求作的三角形.
3、如图,将一个直径AB等于12厘米的半圆绕着点A逆时针旋转60°后,点B落到了点C的位置,半圆扫过部分的图形如阴影部分所示.
( http: / / www.21cnjy.com / )
(1)阴影部分的周长;
(2)阴影部分的面积.(结果保留π)
4、问题背景如图(1),△ABC为等腰直角三 ( http: / / www.21cnjy.com )角形,∠BAC=90°,直线l绕着点A顺时针旋转,过B,C两点分别向直线l作垂线BD,CE,垂足为D,E,此时△ABD可以由△CAE通过旋转变换得到,请写出旋转中心、旋转方向及旋转角的大小(取最小旋转角度).
尝试应用如图(2),△ABC ( http: / / www.21cnjy.com )为等边三角形,直线l绕着点A顺时针旋转,D、E为直线l上两点,∠BDA=∠AEC=60°.△ABD可以由△CAE通过旋转变换得到吗?若可以,请指出旋转中心O的位置并说明理由;
拓展创新如图(3)在问题背景的条件下,若AB=2,连接DC,直接写出CD的长的取值范围.
( http: / / www.21cnjy.com / )
5、下面是小石设计的“过三角形一个顶点作其对边的平行线”的尺规作图过程.
已知:如图,.
( http: / / www.21cnjy.com / )
求作:直线BD,使得.
作法:如图,
( http: / / www.21cnjy.com / )
①分别作线段AC,BC的垂直平分线,,两直线交于点O;
②以点O为圆心,OA长为半径作圆;
③以点A为圆心,BC长为半径作孤,交于点D;
④作直线BD.所以直线BD就是所求作的直线.
根据小石设计的尺规作图过程,
(1)使用直尺和圆规,补全图形;(保留作图痕迹)
(2)完成下面的证明.
证明:连接AD,
∵点A,B,C,D在上,,
∴______.
∴(______)(填推理的依据).
∴.
-参考答案-
一、单选题
1、C
【分析】
根据题意,画出示意图,确定出点的运动路径,再根据弧长公式即可求解.
【详解】
解:根据题意可得,Rt△ABC的运动示意图,如下:
( http: / / www.21cnjy.com / )
Rt△ABC中,∠A=90°,∠B=30°,AC=1,
∴,,,
由图形可得,点的运动路线为,先以为中心,顺时针旋转,到达点,经过的路径长为,再以为中心,顺时针旋转,到达点,经过的路径长为,
顶点A所经过的路径的长为,
故选:C
【点睛】
此题考查了旋转的性质,圆弧弧长的求解,解题的关键是根据题意确定点的运动路线.
2、A
【分析】
根据圆周角定理得到∠ADB=90°,∠A=∠BCD=36°,然后利用互余计算∠ABD的度数.
【详解】
∵AB是⊙O的直径,
∴∠ADB=90°,
∵∠DAB=∠BCD=36°,
∴∠ABD=∠ADB﹣∠DAB,
即∠ABD=90°﹣∠DAB=90°﹣36°=54°.
故选:A.
【点睛】
本题考查了圆周角定理:在 ( http: / / www.21cnjy.com )同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.半圆(或直径)所对的圆周角是直角,90°的圆周角所对的弦是直径.
3、C
【分析】
如图1,△ABC是等边三角形,则∠ABC=60°,根据同弧所对的圆周角相等∠ADC=∠ABC=60°,所以判断①正确;如图1,可证明△DBE∽△DAC,则,所以DB DC=DE DA,而DB与DC不一定相等,所以判断②错误;如图2,作AH⊥BD于点H,延长DB到点K,使BK=CD,连接AK,先证明△ABK≌△ACD,可证明S四边形ABDC=S△ADK,可以求得S△ADK=,所以判断③正确;如图3,连接OA、OG、OC、GC,由CF切⊙O于点C得CF⊥OC,而AF⊥CF,所以AF∥OC,由圆周角定理可得∠AOC=120°,则∠OAC=∠OCA=30°,于是∠CAG=∠OCA=30°,则∠COG=2∠CAG=60°,可证明△AOG和△COG都是等边三角形,则四边形OABC是菱形,因此OA∥CG,推导出S阴影=S扇形COG,在Rt△CFG中根据勾股定理求出CG的长为4,则⊙O的半径为4,可求得S阴影=S扇形COG==,所以判断④正确,所以①③④这3个结论正确.【版权所有:21教育】
【详解】
解:如图1,∵△ABC是等边三角形,
∴∠ABC=60°,
∵等边△ABC内接于⊙O,
∴∠ADC=∠ABC=60°,
故①正确;
∵∠BDE=∠ACB=60°,∠ADC=∠ABC=60°,
∴∠BDE=∠ADC,
又∠DBE=∠DAC,
∴△DBE∽△DAC,
∴,
∴DB DC=DE DA,
∵D是上任一点,
∴DB与DC不一定相等,
∴DB DC与DB2也不一定相等,
∴DB2与DE DA也不一定相等,
故②错误;
( http: / / www.21cnjy.com / )
如图2,作AH⊥BD于点H,延长DB到点K,使BK=CD,连接AK,
∵∠ABK+∠ABD=180°,∠ACD+∠ABD=180°,
∴∠ABK=∠ACD,
∴AB=AC,
∴△ABK≌△ACD(SAS),
∴AK=AD,S△ABK=S△ACD,
∴DH=KH=DK,
( http: / / www.21cnjy.com / )
∵∠AHD=90°,∠ADH=60°,
∴∠DAH=30°,
∵AD=2,
∴DH=AD=1,
∴DK=2DH=2,,
∴S△ADK=,
∴S四边形ABDC=S△ABD+S△ACD=S△ABD+S△ABK=S△ADK=,
故③正确;
如图3,连接OA、OG、OC、GC,则OA=OG=OC,
∵CF切⊙O于点C,
∴CF⊥OC,
∵AF⊥CF,
∴AF∥OC,
∵∠AOC=2∠ABC=120°,
∴∠OAC=∠OCA=×(180°﹣120°)=30°,
∴∠CAG=∠OCA=30°,
∴∠COG=2∠CAG=60°,
∴∠AOG=60°,
∴△AOG和△COG都是等边三角形,
∴OA=OC=AG=CG=OG,
∴四边形OABC是菱形,
∴OA∥CG,
∴S△CAG=S△COG,
∴S阴影=S扇形COG,
∵∠OCF=90°,∠OCG=60°,
∴∠FCG=30°,
∵∠F=90°,
∴FG=CG,
∵FG2+CF2=CG2,CF=,
∴(CG)2+()2=CG2,
∴CG=4,
∴OC=CG=4,
∴S阴影=S扇形COG==,
故④正确,
∴①③④这3个结论正确,
故选C.
( http: / / www.21cnjy.com / )
【点睛】
本题主要考查了等边三角形 ( http: / / www.21cnjy.com )的性质与判定,圆切线的性质,圆周角定理,全等三角形的性质与判定,菱形的性质与判定,勾股定理,含30度角的直角三角形的性质等等,解题的关键在于能够熟练掌握相关知识进行求解.21·cn·jy·com
4、B
【分析】
连接EO,延长EO交CD于F,连接DO,设半径为x.构建方程即可解决问题.
【详解】
解:设⊙O与AB相切于点E.连接EO,延长EO交CD于F,连接DO,
再设⊙O的半径为x.
( http: / / www.21cnjy.com / )
∵AB切⊙O于E,
∴EF⊥AB,
∵AB∥CD,
∴EF⊥CD,
∴∠OFD=90°,
在Rt△DOF中,∵∠OFD=90°,OF2+DF2=OD2,
∴(8-x)2+42= x2,
∴x=5,
∴⊙O的半径为5.
故选:B.
【点睛】
本题考查了切线的性质、正 ( http: / / www.21cnjy.com )方形的性质、垂径定理、勾股定理等知识,解题的关键是灵活运用这些知识解决问题,学会添加常用辅助线,构造直角三角形解决问题.
5、B
【分析】
根据同弧所对的圆周角是圆心角的一半即可得.
【详解】
解:∵,
∴,
∴,
故选:B.
【点睛】
题目主要考查圆周角定理,准确理解,熟练运用圆周角定理是解题关键.
6、C
【分析】
首先证明∠ABD=90°,由∠BOC=50°,根据圆周角定理求出∠A的度数即可解决问题.
【详解】
解:∵BD是切线,
∴BD⊥AB,
∴∠ABD=90°,
∵∠BOC=50°,
∴∠A=∠BOC=25°,
∴∠D=90°﹣∠A=65°,
故选:C.
【点睛】
本题考查的是切线的性质、圆周角定理,解题的关键是灵活应用所学知识解决问题,属于中考常考题型.
7、B
【分析】
先利用多边的内角和得到,可计算出,然后根据圆内接四边形的性质求出的度数即可.
【详解】
解:∵五边形的内角和为,
∴,
∵,
∴,
∵四边形为的内接四边形,
∴,
∴.
故选:B.
【点睛】
本题主要考查了多边形的内角和与圆内接四边形的性质,掌握圆内接四边形的性质是解答本题的关键.
8、B
【分析】
本题可先由勾股定理等性质算出点与圆心 ( http: / / www.21cnjy.com )的距离d,再根据点与圆心的距离与半径的大小关系,即当d>r时,点在圆外;当d=r时,点在圆上;点在圆外;当d<r时,点在圆内;来确定点与圆的位置关系.【出处:21教育名师】
【详解】
解:∵点A(﹣4,﹣3),
∴,
∵⊙A的半径为4,
∴,
∴点O在⊙A外;
故选:B
【点睛】
本题考查了点与圆的位置关系及坐标与图形性质,能够根据勾股定理求得点到圆心的距离,根据数量关系判断点和圆的位置关系.
9、C
【分析】
根据三角形内角和定理求得,根据同弧所对的圆周角相等可得,根据直径所对的圆周角是直角,含30度角的直角三角形的性质,勾股定理即可求得的长
【详解】
解:
为⊙O的直径,
在,, BD=2,
故选C
【点睛】
本题考查了三角形内角和定理,同弧所对的圆周角相等,直径所对的圆周角是直角,勾股定理,含30度角的直角三角形的性质,求得是解题的关键.
10、D
【分析】
根据垂径定理求得CE=ED=;然后由圆周角定理知∠COE=60°.然后通过解直角三角形求得线段OC,然后证明△OCE≌△BDE,得到求出扇形COB面积,即可得出答案.
【详解】
解:设AB与CD交于点E,
∵AB是⊙O的直径,弦CD⊥AB,CD=2,如图,
( http: / / www.21cnjy.com / )
∴CE=CD=,∠CEO=∠DEB=90°,
∵∠CDB=30°,
∴∠COB=2∠CDB=60°,
∴∠OCE=30°,
∴,
∴,
又∵,即
∴,
在△OCE和△BDE中,
,
∴△OCE≌△BDE(AAS),
∴
∴阴影部分的面积S=S扇形COB=,
故选D.
【点睛】
本题考查了垂径定理、含30 ( http: / / www.21cnjy.com )度角的直角三角形的性质,全等三角形的性质与判定,圆周角定理,扇形面积的计算等知识点,能知道阴影部分的面积=扇形COB的面积是解此题的关键.
二、填空题
1、70°度
【分析】
连接OA、OB,根据切线性质可得∠OAP=∠OBP=90°,再根据四边形的内角和为360°求得∠AOB,然后利用圆周角定理求解即可.2·1·c·n·j·y
【详解】
解:连接OA、OB,
∵PA,PB分别切⊙O于点A,B,
∴∠OAP=∠OBP=90°,又∠P=40°,
∴∠AOB=360°-90°-90°-40°=140°,
∴∠Q=∠AOB=70°,
故答案为:70°.
( http: / / www.21cnjy.com / )
【点睛】
本题考查切线性质、四边形内角和为360°、圆周角定理,熟练掌握切线性质和圆周角定理是解答的关键.
2、
【分析】
根据圆内接正五边形的定义求出∠COD,利用三角形内角和求出答案.
【详解】
解:∵五边形是⊙的内接正五边形,
∴∠COD=,
∵OC=OD,
∴=,
故答案为:.
【点睛】
此题考查了圆内接正五边形的性质,三角形内角和定理,同圆的半径相等的性质,熟记圆内接正五边形的性质是解题的关键.【来源:21·世纪·教育·网】
3、①②④
【分析】
连接OM,由切线的性质可得,继而得,再根据平行线的性质以及等边对等角即可求得,由此可判断①;通过证明,根据相似三角形的对应边成比例可判断②;求出,利用弧长公式求得的长可判断③;由,,,可得,继而可得,,进而有,在中,利用勾股定理求出PD的长,可得,由此可判断④.www-2-1-cnjy-com
【详解】
解:连接OM,
( http: / / www.21cnjy.com / )
∵PE为的切线,
∴,
∵,
∴,
∴,
∵,,
∴,
即AM平分,故①正确;
∵AB为的直径,
∴,
∵,,
∴,
∴,
∴,故②正确;
∵,
∴,
∵,
∴,
∴的长为,故③错误;
∵,,,
∴,
∴,
∴,
∴,
又∵,,,
∴,
又∵,
∴,
设,则,
∴,
在中,,
∴,
∴,
由①可得,
,
故④正确,
故答案为:①②④.
【点睛】
本题考查了切线的性质,平行线分线段成比例定理,相似三角形的判定与性质,勾股定理等,正确添加辅助线,熟练掌握和灵活运用相关知识是解题的关键.21世纪教育网版权所有
4、140
【分析】
作的外接圆,根据三角形内心的性质可得:,,再由三角形内角和定理得出:,最后根据三角形外心的性质及圆周角定理即可得.21*cnjy*com
【详解】
解:如图所示,作的外接圆,
( http: / / www.21cnjy.com / )
∵点I是的内心,
∴BI,CI分别平分和,
∴,,
∵,
∴,
∴,
∴,
∵点O是的外心,
∴,
故答案为:140.
【点睛】
题目主要考查三角形内心与外心的性质,三角形内角和定理等,理解题意,熟练掌握三角形内心与外心的性质是解题关键.21*cnjy*com
5、12π
【分析】
根据扇形的面积公式计算即可.
【详解】
∵
=12π,
故答案为:12π.
【点睛】
本题考查了扇形的面积,熟记扇形面积公式是解题的关键.
三、解答题
1、(1);(2)2
【分析】
(1)根据切线长定理可得,则一元二次方程的判别式为0,进而即可求得的值;
(2)根据(1)的结论求得的长,CD与⊙O相切于点E,则,根据△PCD的周长即可求解.
【详解】
解: PA,PB与⊙O相切,
PA,PB的长是关于x的一元二次方程x2﹣mx+m﹣1=0的两个根
解得
(2)
PA,PB与⊙O相切, CD与⊙O相切于点E,
△PCD的周长
【点睛】
本题考查了切线长定理,一元二次方程根的判别式,解一元二次方程,掌握切线长定理是解题的关键.
2、
(1)图形见解析
(2)直径所对的圆周角是直角;三边相等的三角形是等边三角形.
【分析】
(1)根据要求作出图形即可;
(2)根据圆周角定理等边三角形的判定和性质解决问题即可.
(1)
如图,△ABC即为所求作.
( http: / / www.21cnjy.com / )
(2)
∵AB为⊙O的直径,点C在⊙O上,
∴∠ACB=90°(直径所对的圆周角是直角),
连接OC.
∵OA=OC=AC,
∴△AOC为等边三角形(三边相等的三角形是等边三角形),
∴∠A=60°.
故答案为:直径所对的圆周角是直角,三边相等的三角形是等边三角形.
【点睛】
本题考查作图-复杂作图,等边三角形的判定和性质,圆周角定理等知识,解题的关键是理解题意,灵活运用所学知识解决问题.21cnjy.com
3、
(1)16π
(2)24π
【分析】
(1)由阴影部分的周长=两个半圆弧的长度+弧BC的长,利用弧长公式可求解;
(2)由面积的和差关系可求解.
(1)
解:阴影部分的周长=2××2π×6+=16π;
(2)
解:∵阴影部分的面积=S半圆+S扇形BAC﹣S半圆=S扇形BAC,
∴阴影部分的面积==24π.
答:阴影部分的周长为16π,阴影部分的面积为24π.
【点睛】
本题考查了扇形的弧长公式和面积公式,如果扇形的圆心角是n°,扇形的半径为r,则扇形的弧长l的计算公式为:,扇形的面积公式:.21·世纪*教育网
4、(1)旋转中心为BC边的中点O,旋转方向为逆时针,旋转角度为90°;(2)可以,旋转中心为为等边△ABC三边垂直平分线的交点O,理由见解析;(3)2-1-c-n-j-y
【分析】
问题背景(1)根据等腰直角三角形的性质,以及旋转的性质确定即可;
尝试应用(2)首先通过证明△ABD和△CAE全等说明点A和点B对应,点C和点A对应,从而作AB和AC的垂直平分线,其交点即为旋转中点;21教育网
拓展创新(3)首先确定出D点的运动轨迹,然后结合点与圆的位置关系,分别讨论出CD最长和最短时的情况,并结合勾股定理进行求解即可.21教育名师原创作品
【详解】
解:问题背景(1)如图所示,作AO⊥BC,交BC于点O,
由等腰直角三角形的性质可知:∠AOC=90°,OA=OC,
∴点A是由点C绕点O逆时针旋转90°得到,
同理可得,点B是由点A绕点O逆时针旋转90°得到,
点D是由点E绕点O逆时针旋转90°得到,
∴△ABD可以由△CAE通过旋转变换得到,旋转中心为BC边的中点O,旋转方向为逆时针,旋转角度为90°;
( http: / / www.21cnjy.com / )
尝试应用(2)∵△ABC为等边三角形,
∴AB=AC,∠BAC=60°,
∵∠DAC=∠DAB+∠BAC=∠AEC+∠EAC,∠BAC=∠AEC=60°,
∴∠DAB=∠ECA,
在△ABD和△CAE中,
∴△ABD≌△CAE(AAS),
∴△ABD的A、B、D三点的对应点分别为△CAE的C、A、E三点,
则AC、AB分别视作两组对应点的连线,
此时,如图所示,作AC和AB的垂直平分线交于点O,
∵△ABC为等边三角形,
∴由等边三角形的性质可知,OC=OA=OB,∠AOC=120°,
∴△ABD可以由△CAE通过旋转变换得到,旋转中心为为等边△ABC三边垂直平分线的交点O;
( http: / / www.21cnjy.com / )
拓展创新(3)由(1)知,在直线l旋转的过程中,总有∠ADB=90°,
∴点D的运动轨迹为以AB为直径的圆,
如图,取AB的中点P,连接CP,交⊙P于点Q,
则当点D在CP的延长线时,CD的长度最大,
当点D与Q点重合时,CD的长度最小,即CQ的长度,
∵AB=AC,AB=2,
∴AP=1,AC=2,
在Rt△APC中,,
由圆的性质,PD=AP=1,
∴PD=PQ=1,
∴,,
∴CD的长的取值范围为:.
( http: / / www.21cnjy.com / )
【点睛】
本题主要考查旋转三要素的确定,以及旋转的 ( http: / / www.21cnjy.com )性质,主要涉及等腰直角三角形和等边三角形的性质,全等三角形的判定与性质,以及动点最值问题,掌握旋转的性质,确定出动点的轨迹,熟练运用圆的相关知识点是解题关键.
5、(1)作图见解析;(2) 在同圆中,等弧所对的圆周角相等
【分析】
(1)根据题干的作图步骤依次作图即可;
(2)由作图可得,证明,利用圆周角定理可得,从而可得答案.
【详解】
解:(1)如图,直线BD就是所求作的直线
( http: / / www.21cnjy.com / )
(2)证明:连接AD,
∵点A,B,C,D在上,,
∴.
∴(在同圆中,等弧所对的圆周角相等).
∴.
故答案为: 在同圆中,等弧所对的圆周角相等
【点睛】
本题考查的是作线段的垂直平分线,三角形的外接圆,平行线的作图,圆周角定理的应用,掌握“圆周角定理”是理解作图的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
九年级数学第二学期第二十七章圆与正多边形综合测评
考试时间:90分钟;命题人:数学教研组
考生注意:
1、本卷分第I卷(选择题)和第Ⅱ卷(非选择题)两部分,满分100分,考试时间90分钟
2、答卷前,考生务必用0.5毫米黑色签字笔将自己的姓名、班级填写在试卷规定位置上
3、答案必须写在试卷各个题目指定区域内 ( http: / / www.21cnjy.com )相应的位置,如需改动,先划掉原来的答案,然后再写上新的答案;不准使用涂改液、胶带纸、修正带,不按以上要求作答的答案无效。www.21-cn-jy.com
第I卷(选择题 30分)
一、单选题(10小题,每小题3分,共计30分)
1、如图,Rt△ABC中,∠A=90°,∠B ( http: / / www.21cnjy.com )=30°,AC=1,将Rt△ABC延直线l由图1的位置按顺时针方向向右作无滑动滚动,当A第一次滚动到图2位置时,顶点A所经过的路径的长为( )
( http: / / www.21cnjy.com / )
A. B. C. D.(2+)π
2、如图,已知AB是⊙O的直径,CD是弦,若∠BCD=36°,则∠ABD等于( )
( http: / / www.21cnjy.com / )
A.54° B.56° C.64° D.66°
3、如图,等边△ABC内接于⊙O,D是上任一点(不与B、C重合),连接BD、CD,AD交BC于E,CF切⊙O于点C,AF⊥CF交⊙O于点G.下列结论:①∠ADC=60°;②DB2=DE DA;③若AD=2,则四边形ABDC的面积为;④若CF=2,则图中阴影部分的面积为.正确的个数为( )
( http: / / www.21cnjy.com / )
A.1个 B.2个 C.3个 D.4个
4、如图,正方形ABCD的边长为8,若经过C,D两点的⊙O与直线AB相切,则⊙O的半径为( )
( http: / / www.21cnjy.com / )
A.4.8 B.5 C.4 D.4
5、如图,点A,B,C均在⊙O上,连接OA,OB,AC,BC,如果OA⊥OB,那么∠C的度数为( )
( http: / / www.21cnjy.com / )
A.22.5° B.45° C.90° D.67.5°
6、如图,AB是⊙O的直径,BD与⊙O相切于 ( http: / / www.21cnjy.com )点B,点C是⊙O上一点,连接AC并延长,交BD于点D,连接OC,BC,若∠BOC=50°,则∠D的度数为( )【来源:21cnj*y.co*m】
( http: / / www.21cnjy.com / )
A.50° B.55° C.65° D.75°
7、如图,在圆内接五边形中,,则的度数为( )
( http: / / www.21cnjy.com / )
A. B. C. D.
8、在平面直角坐标系xOy中,已知点A(﹣4,﹣3),以点A为圆心,4为半径画⊙A,则坐标原点O与⊙A的位置关系是( )
A.点O在⊙A内 B.点O在⊙A外
C.点O在⊙A上 D.以上都有可能
9、如图,ABC内接于⊙O,,BD为⊙O的直径,且BD=2,则DC=( )
( http: / / www.21cnjy.com / )
A.1 B. C. D.
10、如图,AB是⊙O的直径,弦,,,则阴影部分图形的面积为( )
( http: / / www.21cnjy.com / )
A. B. C. D.
第Ⅱ卷(非选择题 70分)
二、填空题(5小题,每小题4分,共计20分)
1、如图,PA,PB分别切⊙O于点A,B,Q是优弧上一点,若∠P=40°,则∠Q的度数是________.
( http: / / www.21cnjy.com / )
2、如图,五边形是⊙的内接正五边形,则的度数是____.
( http: / / www.21cnjy.com / )
3、如图AB为⊙O的直径 ( http: / / www.21cnjy.com ),点P为AB延长线上的点,过点P作⊙O的切线PE,切点为M,过A、B两点分别作PE垂线AC、BD,垂足分别为C、D,连接AM,则下列结论正确的是______(写所有正确论的号)
①AM平分∠CAB;②;③若AB=4,∠APE=30°,则的长为;④若AC=3BD,则有tan∠MAP=.
( http: / / www.21cnjy.com / )
4、已知O、I分别是△ABC的外心和内心,∠BIC=125°,则∠BOC的大小是 ___度.
5、圆形角是270°的扇形的半径为4cm,则这个扇形的面积是______.
三、解答题(5小题,每小题10分,共计50分)
1、如图,PA,PB与⊙O ( http: / / www.21cnjy.com )相切,切点为A,B,CD与⊙O相切于点E,分别交PA,PB于点D,C.若PA,PB的长是关于x的一元二次方程x2﹣mx+m﹣1=0的两个根.
(1)求m的值;
(2)求△PCD的周长.
( http: / / www.21cnjy.com / )
2、已知:如图,射线.
求作:,使得点在射线上,,.
作法:①在射线上任取一点;
②以点为圆心,的长为半径画圆,交射线于另一点;
③以点为圆心,的长为半径画弧,在射线上方交于点;
④连接、.
(1)使用直尺和圆规,依作法补全图形(保留作图痕迹);
(2)完成下面的证明.
证明:为的直径,点在上,
(___________________________)(填推理依据).
连接.
,
为等边三角形(___________________________)(填推理依据).
所以为所求作的三角形.
3、如图,将一个直径AB等于12厘米的半圆绕着点A逆时针旋转60°后,点B落到了点C的位置,半圆扫过部分的图形如阴影部分所示.
( http: / / www.21cnjy.com / )
(1)阴影部分的周长;
(2)阴影部分的面积.(结果保留π)
4、问题背景如图(1),△ABC为等腰直角三 ( http: / / www.21cnjy.com )角形,∠BAC=90°,直线l绕着点A顺时针旋转,过B,C两点分别向直线l作垂线BD,CE,垂足为D,E,此时△ABD可以由△CAE通过旋转变换得到,请写出旋转中心、旋转方向及旋转角的大小(取最小旋转角度).
尝试应用如图(2),△ABC ( http: / / www.21cnjy.com )为等边三角形,直线l绕着点A顺时针旋转,D、E为直线l上两点,∠BDA=∠AEC=60°.△ABD可以由△CAE通过旋转变换得到吗?若可以,请指出旋转中心O的位置并说明理由;
拓展创新如图(3)在问题背景的条件下,若AB=2,连接DC,直接写出CD的长的取值范围.
( http: / / www.21cnjy.com / )
5、下面是小石设计的“过三角形一个顶点作其对边的平行线”的尺规作图过程.
已知:如图,.
( http: / / www.21cnjy.com / )
求作:直线BD,使得.
作法:如图,
( http: / / www.21cnjy.com / )
①分别作线段AC,BC的垂直平分线,,两直线交于点O;
②以点O为圆心,OA长为半径作圆;
③以点A为圆心,BC长为半径作孤,交于点D;
④作直线BD.所以直线BD就是所求作的直线.
根据小石设计的尺规作图过程,
(1)使用直尺和圆规,补全图形;(保留作图痕迹)
(2)完成下面的证明.
证明:连接AD,
∵点A,B,C,D在上,,
∴______.
∴(______)(填推理的依据).
∴.
-参考答案-
一、单选题
1、C
【分析】
根据题意,画出示意图,确定出点的运动路径,再根据弧长公式即可求解.
【详解】
解:根据题意可得,Rt△ABC的运动示意图,如下:
( http: / / www.21cnjy.com / )
Rt△ABC中,∠A=90°,∠B=30°,AC=1,
∴,,,
由图形可得,点的运动路线为,先以为中心,顺时针旋转,到达点,经过的路径长为,再以为中心,顺时针旋转,到达点,经过的路径长为,
顶点A所经过的路径的长为,
故选:C
【点睛】
此题考查了旋转的性质,圆弧弧长的求解,解题的关键是根据题意确定点的运动路线.
2、A
【分析】
根据圆周角定理得到∠ADB=90°,∠A=∠BCD=36°,然后利用互余计算∠ABD的度数.
【详解】
∵AB是⊙O的直径,
∴∠ADB=90°,
∵∠DAB=∠BCD=36°,
∴∠ABD=∠ADB﹣∠DAB,
即∠ABD=90°﹣∠DAB=90°﹣36°=54°.
故选:A.
【点睛】
本题考查了圆周角定理:在 ( http: / / www.21cnjy.com )同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.半圆(或直径)所对的圆周角是直角,90°的圆周角所对的弦是直径.
3、C
【分析】
如图1,△ABC是等边三角形,则∠ABC=60°,根据同弧所对的圆周角相等∠ADC=∠ABC=60°,所以判断①正确;如图1,可证明△DBE∽△DAC,则,所以DB DC=DE DA,而DB与DC不一定相等,所以判断②错误;如图2,作AH⊥BD于点H,延长DB到点K,使BK=CD,连接AK,先证明△ABK≌△ACD,可证明S四边形ABDC=S△ADK,可以求得S△ADK=,所以判断③正确;如图3,连接OA、OG、OC、GC,由CF切⊙O于点C得CF⊥OC,而AF⊥CF,所以AF∥OC,由圆周角定理可得∠AOC=120°,则∠OAC=∠OCA=30°,于是∠CAG=∠OCA=30°,则∠COG=2∠CAG=60°,可证明△AOG和△COG都是等边三角形,则四边形OABC是菱形,因此OA∥CG,推导出S阴影=S扇形COG,在Rt△CFG中根据勾股定理求出CG的长为4,则⊙O的半径为4,可求得S阴影=S扇形COG==,所以判断④正确,所以①③④这3个结论正确.【版权所有:21教育】
【详解】
解:如图1,∵△ABC是等边三角形,
∴∠ABC=60°,
∵等边△ABC内接于⊙O,
∴∠ADC=∠ABC=60°,
故①正确;
∵∠BDE=∠ACB=60°,∠ADC=∠ABC=60°,
∴∠BDE=∠ADC,
又∠DBE=∠DAC,
∴△DBE∽△DAC,
∴,
∴DB DC=DE DA,
∵D是上任一点,
∴DB与DC不一定相等,
∴DB DC与DB2也不一定相等,
∴DB2与DE DA也不一定相等,
故②错误;
( http: / / www.21cnjy.com / )
如图2,作AH⊥BD于点H,延长DB到点K,使BK=CD,连接AK,
∵∠ABK+∠ABD=180°,∠ACD+∠ABD=180°,
∴∠ABK=∠ACD,
∴AB=AC,
∴△ABK≌△ACD(SAS),
∴AK=AD,S△ABK=S△ACD,
∴DH=KH=DK,
( http: / / www.21cnjy.com / )
∵∠AHD=90°,∠ADH=60°,
∴∠DAH=30°,
∵AD=2,
∴DH=AD=1,
∴DK=2DH=2,,
∴S△ADK=,
∴S四边形ABDC=S△ABD+S△ACD=S△ABD+S△ABK=S△ADK=,
故③正确;
如图3,连接OA、OG、OC、GC,则OA=OG=OC,
∵CF切⊙O于点C,
∴CF⊥OC,
∵AF⊥CF,
∴AF∥OC,
∵∠AOC=2∠ABC=120°,
∴∠OAC=∠OCA=×(180°﹣120°)=30°,
∴∠CAG=∠OCA=30°,
∴∠COG=2∠CAG=60°,
∴∠AOG=60°,
∴△AOG和△COG都是等边三角形,
∴OA=OC=AG=CG=OG,
∴四边形OABC是菱形,
∴OA∥CG,
∴S△CAG=S△COG,
∴S阴影=S扇形COG,
∵∠OCF=90°,∠OCG=60°,
∴∠FCG=30°,
∵∠F=90°,
∴FG=CG,
∵FG2+CF2=CG2,CF=,
∴(CG)2+()2=CG2,
∴CG=4,
∴OC=CG=4,
∴S阴影=S扇形COG==,
故④正确,
∴①③④这3个结论正确,
故选C.
( http: / / www.21cnjy.com / )
【点睛】
本题主要考查了等边三角形 ( http: / / www.21cnjy.com )的性质与判定,圆切线的性质,圆周角定理,全等三角形的性质与判定,菱形的性质与判定,勾股定理,含30度角的直角三角形的性质等等,解题的关键在于能够熟练掌握相关知识进行求解.21·cn·jy·com
4、B
【分析】
连接EO,延长EO交CD于F,连接DO,设半径为x.构建方程即可解决问题.
【详解】
解:设⊙O与AB相切于点E.连接EO,延长EO交CD于F,连接DO,
再设⊙O的半径为x.
( http: / / www.21cnjy.com / )
∵AB切⊙O于E,
∴EF⊥AB,
∵AB∥CD,
∴EF⊥CD,
∴∠OFD=90°,
在Rt△DOF中,∵∠OFD=90°,OF2+DF2=OD2,
∴(8-x)2+42= x2,
∴x=5,
∴⊙O的半径为5.
故选:B.
【点睛】
本题考查了切线的性质、正 ( http: / / www.21cnjy.com )方形的性质、垂径定理、勾股定理等知识,解题的关键是灵活运用这些知识解决问题,学会添加常用辅助线,构造直角三角形解决问题.
5、B
【分析】
根据同弧所对的圆周角是圆心角的一半即可得.
【详解】
解:∵,
∴,
∴,
故选:B.
【点睛】
题目主要考查圆周角定理,准确理解,熟练运用圆周角定理是解题关键.
6、C
【分析】
首先证明∠ABD=90°,由∠BOC=50°,根据圆周角定理求出∠A的度数即可解决问题.
【详解】
解:∵BD是切线,
∴BD⊥AB,
∴∠ABD=90°,
∵∠BOC=50°,
∴∠A=∠BOC=25°,
∴∠D=90°﹣∠A=65°,
故选:C.
【点睛】
本题考查的是切线的性质、圆周角定理,解题的关键是灵活应用所学知识解决问题,属于中考常考题型.
7、B
【分析】
先利用多边的内角和得到,可计算出,然后根据圆内接四边形的性质求出的度数即可.
【详解】
解:∵五边形的内角和为,
∴,
∵,
∴,
∵四边形为的内接四边形,
∴,
∴.
故选:B.
【点睛】
本题主要考查了多边形的内角和与圆内接四边形的性质,掌握圆内接四边形的性质是解答本题的关键.
8、B
【分析】
本题可先由勾股定理等性质算出点与圆心 ( http: / / www.21cnjy.com )的距离d,再根据点与圆心的距离与半径的大小关系,即当d>r时,点在圆外;当d=r时,点在圆上;点在圆外;当d<r时,点在圆内;来确定点与圆的位置关系.【出处:21教育名师】
【详解】
解:∵点A(﹣4,﹣3),
∴,
∵⊙A的半径为4,
∴,
∴点O在⊙A外;
故选:B
【点睛】
本题考查了点与圆的位置关系及坐标与图形性质,能够根据勾股定理求得点到圆心的距离,根据数量关系判断点和圆的位置关系.
9、C
【分析】
根据三角形内角和定理求得,根据同弧所对的圆周角相等可得,根据直径所对的圆周角是直角,含30度角的直角三角形的性质,勾股定理即可求得的长
【详解】
解:
为⊙O的直径,
在,, BD=2,
故选C
【点睛】
本题考查了三角形内角和定理,同弧所对的圆周角相等,直径所对的圆周角是直角,勾股定理,含30度角的直角三角形的性质,求得是解题的关键.
10、D
【分析】
根据垂径定理求得CE=ED=;然后由圆周角定理知∠COE=60°.然后通过解直角三角形求得线段OC,然后证明△OCE≌△BDE,得到求出扇形COB面积,即可得出答案.
【详解】
解:设AB与CD交于点E,
∵AB是⊙O的直径,弦CD⊥AB,CD=2,如图,
( http: / / www.21cnjy.com / )
∴CE=CD=,∠CEO=∠DEB=90°,
∵∠CDB=30°,
∴∠COB=2∠CDB=60°,
∴∠OCE=30°,
∴,
∴,
又∵,即
∴,
在△OCE和△BDE中,
,
∴△OCE≌△BDE(AAS),
∴
∴阴影部分的面积S=S扇形COB=,
故选D.
【点睛】
本题考查了垂径定理、含30 ( http: / / www.21cnjy.com )度角的直角三角形的性质,全等三角形的性质与判定,圆周角定理,扇形面积的计算等知识点,能知道阴影部分的面积=扇形COB的面积是解此题的关键.
二、填空题
1、70°度
【分析】
连接OA、OB,根据切线性质可得∠OAP=∠OBP=90°,再根据四边形的内角和为360°求得∠AOB,然后利用圆周角定理求解即可.2·1·c·n·j·y
【详解】
解:连接OA、OB,
∵PA,PB分别切⊙O于点A,B,
∴∠OAP=∠OBP=90°,又∠P=40°,
∴∠AOB=360°-90°-90°-40°=140°,
∴∠Q=∠AOB=70°,
故答案为:70°.
( http: / / www.21cnjy.com / )
【点睛】
本题考查切线性质、四边形内角和为360°、圆周角定理,熟练掌握切线性质和圆周角定理是解答的关键.
2、
【分析】
根据圆内接正五边形的定义求出∠COD,利用三角形内角和求出答案.
【详解】
解:∵五边形是⊙的内接正五边形,
∴∠COD=,
∵OC=OD,
∴=,
故答案为:.
【点睛】
此题考查了圆内接正五边形的性质,三角形内角和定理,同圆的半径相等的性质,熟记圆内接正五边形的性质是解题的关键.【来源:21·世纪·教育·网】
3、①②④
【分析】
连接OM,由切线的性质可得,继而得,再根据平行线的性质以及等边对等角即可求得,由此可判断①;通过证明,根据相似三角形的对应边成比例可判断②;求出,利用弧长公式求得的长可判断③;由,,,可得,继而可得,,进而有,在中,利用勾股定理求出PD的长,可得,由此可判断④.www-2-1-cnjy-com
【详解】
解:连接OM,
( http: / / www.21cnjy.com / )
∵PE为的切线,
∴,
∵,
∴,
∴,
∵,,
∴,
即AM平分,故①正确;
∵AB为的直径,
∴,
∵,,
∴,
∴,
∴,故②正确;
∵,
∴,
∵,
∴,
∴的长为,故③错误;
∵,,,
∴,
∴,
∴,
∴,
又∵,,,
∴,
又∵,
∴,
设,则,
∴,
在中,,
∴,
∴,
由①可得,
,
故④正确,
故答案为:①②④.
【点睛】
本题考查了切线的性质,平行线分线段成比例定理,相似三角形的判定与性质,勾股定理等,正确添加辅助线,熟练掌握和灵活运用相关知识是解题的关键.21世纪教育网版权所有
4、140
【分析】
作的外接圆,根据三角形内心的性质可得:,,再由三角形内角和定理得出:,最后根据三角形外心的性质及圆周角定理即可得.21*cnjy*com
【详解】
解:如图所示,作的外接圆,
( http: / / www.21cnjy.com / )
∵点I是的内心,
∴BI,CI分别平分和,
∴,,
∵,
∴,
∴,
∴,
∵点O是的外心,
∴,
故答案为:140.
【点睛】
题目主要考查三角形内心与外心的性质,三角形内角和定理等,理解题意,熟练掌握三角形内心与外心的性质是解题关键.21*cnjy*com
5、12π
【分析】
根据扇形的面积公式计算即可.
【详解】
∵
=12π,
故答案为:12π.
【点睛】
本题考查了扇形的面积,熟记扇形面积公式是解题的关键.
三、解答题
1、(1);(2)2
【分析】
(1)根据切线长定理可得,则一元二次方程的判别式为0,进而即可求得的值;
(2)根据(1)的结论求得的长,CD与⊙O相切于点E,则,根据△PCD的周长即可求解.
【详解】
解: PA,PB与⊙O相切,
PA,PB的长是关于x的一元二次方程x2﹣mx+m﹣1=0的两个根
解得
(2)
PA,PB与⊙O相切, CD与⊙O相切于点E,
△PCD的周长
【点睛】
本题考查了切线长定理,一元二次方程根的判别式,解一元二次方程,掌握切线长定理是解题的关键.
2、
(1)图形见解析
(2)直径所对的圆周角是直角;三边相等的三角形是等边三角形.
【分析】
(1)根据要求作出图形即可;
(2)根据圆周角定理等边三角形的判定和性质解决问题即可.
(1)
如图,△ABC即为所求作.
( http: / / www.21cnjy.com / )
(2)
∵AB为⊙O的直径,点C在⊙O上,
∴∠ACB=90°(直径所对的圆周角是直角),
连接OC.
∵OA=OC=AC,
∴△AOC为等边三角形(三边相等的三角形是等边三角形),
∴∠A=60°.
故答案为:直径所对的圆周角是直角,三边相等的三角形是等边三角形.
【点睛】
本题考查作图-复杂作图,等边三角形的判定和性质,圆周角定理等知识,解题的关键是理解题意,灵活运用所学知识解决问题.21cnjy.com
3、
(1)16π
(2)24π
【分析】
(1)由阴影部分的周长=两个半圆弧的长度+弧BC的长,利用弧长公式可求解;
(2)由面积的和差关系可求解.
(1)
解:阴影部分的周长=2××2π×6+=16π;
(2)
解:∵阴影部分的面积=S半圆+S扇形BAC﹣S半圆=S扇形BAC,
∴阴影部分的面积==24π.
答:阴影部分的周长为16π,阴影部分的面积为24π.
【点睛】
本题考查了扇形的弧长公式和面积公式,如果扇形的圆心角是n°,扇形的半径为r,则扇形的弧长l的计算公式为:,扇形的面积公式:.21·世纪*教育网
4、(1)旋转中心为BC边的中点O,旋转方向为逆时针,旋转角度为90°;(2)可以,旋转中心为为等边△ABC三边垂直平分线的交点O,理由见解析;(3)2-1-c-n-j-y
【分析】
问题背景(1)根据等腰直角三角形的性质,以及旋转的性质确定即可;
尝试应用(2)首先通过证明△ABD和△CAE全等说明点A和点B对应,点C和点A对应,从而作AB和AC的垂直平分线,其交点即为旋转中点;21教育网
拓展创新(3)首先确定出D点的运动轨迹,然后结合点与圆的位置关系,分别讨论出CD最长和最短时的情况,并结合勾股定理进行求解即可.21教育名师原创作品
【详解】
解:问题背景(1)如图所示,作AO⊥BC,交BC于点O,
由等腰直角三角形的性质可知:∠AOC=90°,OA=OC,
∴点A是由点C绕点O逆时针旋转90°得到,
同理可得,点B是由点A绕点O逆时针旋转90°得到,
点D是由点E绕点O逆时针旋转90°得到,
∴△ABD可以由△CAE通过旋转变换得到,旋转中心为BC边的中点O,旋转方向为逆时针,旋转角度为90°;
( http: / / www.21cnjy.com / )
尝试应用(2)∵△ABC为等边三角形,
∴AB=AC,∠BAC=60°,
∵∠DAC=∠DAB+∠BAC=∠AEC+∠EAC,∠BAC=∠AEC=60°,
∴∠DAB=∠ECA,
在△ABD和△CAE中,
∴△ABD≌△CAE(AAS),
∴△ABD的A、B、D三点的对应点分别为△CAE的C、A、E三点,
则AC、AB分别视作两组对应点的连线,
此时,如图所示,作AC和AB的垂直平分线交于点O,
∵△ABC为等边三角形,
∴由等边三角形的性质可知,OC=OA=OB,∠AOC=120°,
∴△ABD可以由△CAE通过旋转变换得到,旋转中心为为等边△ABC三边垂直平分线的交点O;
( http: / / www.21cnjy.com / )
拓展创新(3)由(1)知,在直线l旋转的过程中,总有∠ADB=90°,
∴点D的运动轨迹为以AB为直径的圆,
如图,取AB的中点P,连接CP,交⊙P于点Q,
则当点D在CP的延长线时,CD的长度最大,
当点D与Q点重合时,CD的长度最小,即CQ的长度,
∵AB=AC,AB=2,
∴AP=1,AC=2,
在Rt△APC中,,
由圆的性质,PD=AP=1,
∴PD=PQ=1,
∴,,
∴CD的长的取值范围为:.
( http: / / www.21cnjy.com / )
【点睛】
本题主要考查旋转三要素的确定,以及旋转的 ( http: / / www.21cnjy.com )性质,主要涉及等腰直角三角形和等边三角形的性质,全等三角形的判定与性质,以及动点最值问题,掌握旋转的性质,确定出动点的轨迹,熟练运用圆的相关知识点是解题关键.
5、(1)作图见解析;(2) 在同圆中,等弧所对的圆周角相等
【分析】
(1)根据题干的作图步骤依次作图即可;
(2)由作图可得,证明,利用圆周角定理可得,从而可得答案.
【详解】
解:(1)如图,直线BD就是所求作的直线
( http: / / www.21cnjy.com / )
(2)证明:连接AD,
∵点A,B,C,D在上,,
∴.
∴(在同圆中,等弧所对的圆周角相等).
∴.
故答案为: 在同圆中,等弧所对的圆周角相等
【点睛】
本题考查的是作线段的垂直平分线,三角形的外接圆,平行线的作图,圆周角定理的应用,掌握“圆周角定理”是理解作图的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
