【精品解析】沪教版(上海)九下 第二十七章 圆与正多边形必考点解析试题(含解析)
文档属性
| 名称 | 【精品解析】沪教版(上海)九下 第二十七章 圆与正多边形必考点解析试题(含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 2.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-19 13:43:13 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
九年级数学第二学期第二十七章圆与正多边形必考点解析
考试时间:90分钟;命题人:数学教研组
考生注意:
1、本卷分第I卷(选择题)和第Ⅱ卷(非选择题)两部分,满分100分,考试时间90分钟
2、答卷前,考生务必用0.5毫米黑色签字笔将自己的姓名、班级填写在试卷规定位置上
3、答案必须写在试卷各个 ( http: / / www.21cnjy.com )题目指定区域内相应的位置,如需改动,先划掉原来的答案,然后再写上新的答案;不准使用涂改液、胶带纸、修正带,不按以上要求作答的答案无效。21·世纪*教育网
第I卷(选择题 30分)
一、单选题(10小题,每小题3分,共计30分)
1、如图,四边形ABCD内接于,若,则的度数为( )
( http: / / www.21cnjy.com / )
A.50° B.100° C.130° D.150°
2、如图,点A、B、C在⊙O上,∠BAC=56°,则∠BOC的度数为( )
( http: / / www.21cnjy.com / )
A.28° B.102° C.112° D.128°
3、如图,正的边长为,边长为的正的顶点R与点A重合,点P,Q分别在AC,AB上,将沿着边AB,BC,CA连续翻转(如图所示),直至点P第一次回到原来的位置,则点P运动路径的长为( )2-1-c-n-j-y
( http: / / www.21cnjy.com / )
A. B. C. D.
4、如图,在中,,,.将绕点按逆时针方向旋转后得到,则图中阴影部分面积为( )【出处:21教育名师】
( http: / / www.21cnjy.com / )
A. B. C. D.
5、下列说法正确的个数有( )
①方程的两个实数根的和等于1;
②半圆是弧;
③正八边形是中心对称图形;
④“抛掷3枚质地均匀的硬币全部正面朝上”是随机事件;
⑤如果反比例函数的图象经过点,则这个函数图象位于第二、四象限.
A.2个 B.3个 C.4个 D.5个
6、已知正三角形外接圆半径为,这个正三角形的边长是( )
A. B. C. D.
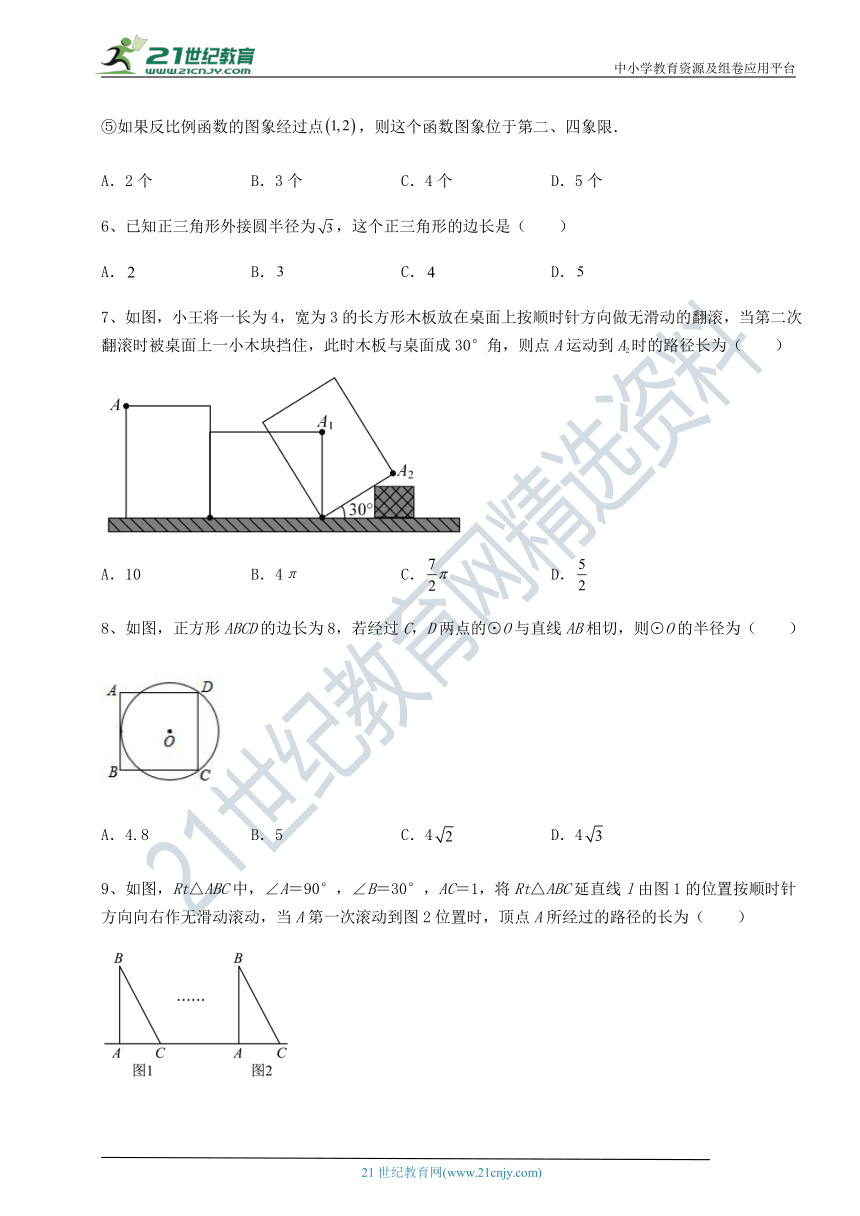
7、如图,小王将一长为4,宽为 ( http: / / www.21cnjy.com )3的长方形木板放在桌面上按顺时针方向做无滑动的翻滚,当第二次翻滚时被桌面上一小木块挡住,此时木板与桌面成30°角,则点A运动到A2时的路径长为( )
( http: / / www.21cnjy.com / )
A.10 B.4π C. D.
8、如图,正方形ABCD的边长为8,若经过C,D两点的⊙O与直线AB相切,则⊙O的半径为( )
( http: / / www.21cnjy.com / )
A.4.8 B.5 C.4 D.4
9、如图,Rt△ABC中,∠A=90 ( http: / / www.21cnjy.com )°,∠B=30°,AC=1,将Rt△ABC延直线l由图1的位置按顺时针方向向右作无滑动滚动,当A第一次滚动到图2位置时,顶点A所经过的路径的长为( )
( http: / / www.21cnjy.com / )
A. B. C. D.(2+)π
10、下列叙述正确的有( )个.
(1)随着的增大而增大;
(2)如果直角三角形斜边的长是斜边上的高的4倍,那么这个三角形两个锐角的度数分别是和;
(3)斜边为的直角三角形顶点的轨迹是以中点为圆心,长为直径的圆;
(4)三角形三边的垂直平分线的交点到三角形三个顶点的距离相等;
(5)以为三边长度的三角形,不是直角三角形.
A.0 B.1 C.2 D.3
第Ⅱ卷(非选择题 70分)
二、填空题(5小题,每小题4分,共计20分)
1、斛是中国古代的一种量 ( http: / / www.21cnjy.com )器.据《汉书 .律历志》记载:“斛底,方而圜(huán)其外,旁有庣(tiāo)焉”.意思是说:“斛的底面为:正方形外接一个圆,此圆外是一个同心圆” . 如图所示,
问题:现有一斛,其底面的 ( http: / / www.21cnjy.com )外圆直径为两尺五寸(即2.5尺),“庣旁”为两寸五分(即两同心圆的外圆与内圆的半径之差为0.25尺),则此斛底面的正方形的边长为________尺.
( http: / / www.21cnjy.com / )
2、如图,AB是⊙O的直径,AT是⊙O的切 ( http: / / www.21cnjy.com )线,∠ABT=50°,BT交⊙O于点C,点E是AB上一点,延长CE交⊙O于点D,则∠CDB=___.21教育网
( http: / / www.21cnjy.com / )
3、如图,点D是⊙O上一点,C是弧AB的中点,若∠ACB=116°,则∠BDC的度数是 _____°.
( http: / / www.21cnjy.com / )
4、如图,正方形ABCD的边长为 ( http: / / www.21cnjy.com )4,点E是CD边上一点,连接AE,过点B作BG⊥AE于点G,连接CG并延长交AD于点F,则AF的最大值是_______.2·1·c·n·j·y
( http: / / www.21cnjy.com / )
5、已知⊙A的半径为5,圆心A(4,3),坐标原点O与⊙A的位置关系是______.
三、解答题(5小题,每小题10分,共计50分)
1、已知直线m与⊙O,AB是⊙O的直径,AD⊥m于点D.
(1)如图①,当直线m与⊙O相交于点E、F时,求证:∠DAE=∠BAF.
(2)如图②,当直线m与⊙O相切于点C时,若∠DAC=35°,求∠BAC的大小;
(3)若PC=2,PB=2,求阴影部分的面积(结果保留π).
( http: / / www.21cnjy.com / )
2、在平面直角坐标系xOy中,图形W ( http: / / www.21cnjy.com )上任意两点间的距离有最大值,将这个最大值记为d.对点P及图形W给出如下定义:点Q为图形W上任意一点,若P,Q两点间的距离有最大值,且最大值恰好为2d,则称点P为图形W的“倍点”.【版权所有:21教育】
(1)如图1,图形W是半径为1的⊙O.
①图形W上任意两点间的距离的最大值d为_________;
②在点(0,2) ,(3,3),(,0)中,⊙O的“倍点”是________;
(2)如图2,图形W是中心在原点的正方形ABCD,已知点A(,1),若点E(,3) 是正方形ABCD的“倍点”,求的值;
(3)图形W是长为2的线段MN,T为MN的中点,若在半径为6的⊙O上存在MN的“倍点”,直接写出满足条件的点T所构成的图形的面积.
( http: / / www.21cnjy.com / )
3、请阅读下列材料,并完成相应的任务:
阿基米德是有史以来最伟大的数学家之一,他与牛顿、高斯并称为三大数21世纪教育网子.阿拉伯Al-Binmi (973-1050 年)的译文中保存了阿基米德折弦定理的内容,苏联在1964年根据Al-Binmi详本出版了俄文版《阿基米德全集》.第一题就是阿基米德折弦定理.阿基米德折弦定理:如图1,和是的两条弦(即折线是圆的一条折弦),, 是的中点,则从向所作垂线的垂足是折弦的中点,即.
下面是运用“截长法”证明的部分证明过程.
证明:如图2,在上截取,连接和.
是的中点,
…
( http: / / www.21cnjy.com / )
任务:
(1)请按照上面的证明思路,写出该证明部分;
(2)填空:如图3,已知等边内接于,,为上一点,,于点,则的周长是_________.
( http: / / www.21cnjy.com / )
4、已知AB是⊙O的直径,点C是圆O上一点,点P为⊙O外一点,且OP∥BC,∠P=∠BAC.
(1)求证:PA为⊙O的切线;
(2)如果OP=AB=6,求图中阴影部分面积.
( http: / / www.21cnjy.com / )
5、如图,为⊙O的直径,半径于O,⊙O的弦与相交于点F,⊙O的切线交的延长线于点E.
( http: / / www.21cnjy.com / )
(1)求证:;
(2)若⊙O的半径长为3,且,求的长.
-参考答案-
一、单选题
1、B
【分析】
根据圆内接四边形的性质求出∠A的度数,根据圆周角定理计算即可.
【详解】
解:∵四边形ABCD内接于⊙O,
∴∠A+∠DCB=180°,
∵∠DCB=130°,
∴∠A=50°,
由圆周角定理得,=2∠A=100°,
故选:B.
【点睛】
本题考查的是圆内接四边形的性质和圆周角定理,掌握圆内接四边形的对角互补是解题的关键.
2、C
【分析】
直接由圆周角定理求解即可.
【详解】
解:∵∠A=56°,∠A与∠BOC所对的弧相同,
∴∠BOC=2∠A=112°,
故选:C.
【点睛】
此题考查了圆周角定理,熟练掌握圆周角定理是解答本题的关键,同圆或等圆中,同弧或等弧所对的圆周角等于这条弧所对的圆心角的一半.21·cn·jy·com
3、B
【分析】
从图中可以看出在AB边,翻转 ( http: / / www.21cnjy.com )的第一次是一个120度的圆心角,半径是1,第二次是以点P为圆心,所以没有路程,同理在AC和BC上也是相同的情况,由此求解即可.21*cnjy*com
【详解】
解:从图中可以看出在AB边,翻转的第一次是一个120度的圆心角,半径是1,所以弧长=,第二次是以点P为圆心,所以没有路程,在BC边上,第一次,第二次同样没有路程,AC边上也是如此,点P运动路径的长为×3=2π.21*cnjy*com
故选:B.
【点睛】
本题主要考查了等边三角形的性质,求弧长,解题的关键在于能够根据题意得到P点的运动轨迹.
4、B
【分析】
阴影部分的面积=扇形扇形,根据旋转性质以及直角三角形的性质,分别求出对应扇形的面积以及的面积,最后即可求出阴影部分的面积.
【详解】
解:由图可知:阴影部分的面积=扇形扇形,
由旋转性质可知:,,
,,
在中,,,,
,,
有勾股定理可知:,
阴影部分的面积=扇形扇形
.
故选:B.
【点睛】
本题主要是考查了旋转性质以及扇形面积公式,熟练利用旋转性质,得到对应扇形的半径和圆心角度数,利用扇形公式求解面积,这是解决本题的关键.
5、B
【分析】
根据所学知识对五个命题进行判断即可.
【详解】
1、,故方程无实数根,故本命题错误;
2、圆上任意两点间的部分叫做圆弧,半圆也是,故本命题正确;
3、八边形绕中心旋转180°以后仍然与原图重合,故本命题正确;
4、抛硬币无论抛多少,出现正反面朝上都是随机事件,故抛三枚硬币全部正面朝上也是随机事件,故本命题正确;
5、反比例函数的图象经过点 (1,2) ,则,它的函数图像位于一三象限,故本命题错误
综上所述,正确个数为3
故选B
【点睛】
本题考查一元二次函数判别式、弧的定义、中心对称图形判断、随机事件理解、反比例函数图像,掌握这些是本题关键.
6、B
【分析】
如图, 为正三角形ABC的外接圆,过点O作OD⊥AB于点D,连接OA, 再由等边三角形的性质,可得∠OAB=30°,,然后根据锐角三角函数,即可求解.www-2-1-cnjy-com
【详解】
解:如图, 为正三角形ABC的外接圆,过点O作OD⊥AB于点D,连接OA,
( http: / / www.21cnjy.com / )
根据题意得:OA= ,∠OAB=30°,,
在中,
,
∴AB=3,即这个正三角形的边长是3.
故选:B
【点睛】
本题主要考查了锐角三角函数,三角形的外接圆,熟练掌握锐角三角函数,三角形的外接圆性质是解题的关键.
7、C
【分析】
根据题意可得:第一次转动的路径是以点B为圆心,AB长为半径的弧长,此时圆心角 ,第二次转动的路径是以点C为圆心,A1C长为半径的弧长,此时圆心角 ,再由弧长公式,即可求解.
【详解】
解:如图,
( http: / / www.21cnjy.com / )
根据题意得: , ,
第一次转动的路径是以点B为圆心,AB长为半径的弧长,此时圆心角 ,
∴ ,
第二次转动的路径是以点C为圆心,A1C长为半径的弧长,此时圆心角 ,
∴ ,
∴点A运动到A2时的路径长为 .
故选:C
【点睛】
本题主要考查了求弧长,熟练掌握扇形的弧长公式是解题的关键.
8、B
【分析】
连接EO,延长EO交CD于F,连接DO,设半径为x.构建方程即可解决问题.
【详解】
解:设⊙O与AB相切于点E.连接EO,延长EO交CD于F,连接DO,
再设⊙O的半径为x.
( http: / / www.21cnjy.com / )
∵AB切⊙O于E,
∴EF⊥AB,
∵AB∥CD,
∴EF⊥CD,
∴∠OFD=90°,
在Rt△DOF中,∵∠OFD=90°,OF2+DF2=OD2,
∴(8-x)2+42= x2,
∴x=5,
∴⊙O的半径为5.
故选:B.
【点睛】
本题考查了切线的性质、正方形的性质、垂径定 ( http: / / www.21cnjy.com )理、勾股定理等知识,解题的关键是灵活运用这些知识解决问题,学会添加常用辅助线,构造直角三角形解决问题.【来源:21·世纪·教育·网】
9、C
【分析】
根据题意,画出示意图,确定出点的运动路径,再根据弧长公式即可求解.
【详解】
解:根据题意可得,Rt△ABC的运动示意图,如下:
( http: / / www.21cnjy.com / )
Rt△ABC中,∠A=90°,∠B=30°,AC=1,
∴,,,
由图形可得,点的运动路线为,先以为中心,顺时针旋转,到达点,经过的路径长为,再以为中心,顺时针旋转,到达点,经过的路径长为,
顶点A所经过的路径的长为,
故选:C
【点睛】
此题考查了旋转的性质,圆弧弧长的求解,解题的关键是根据题意确定点的运动路线.
10、D
【分析】
根据反比例函数的性质,得当或者时,随着的增大而增大;根据直径所对圆周角为直角的性质,得斜边为的直角三角形顶点的轨迹是以中点为圆心,长为直径的圆;根据垂直平分线的性质,得三角形三边的垂直平分线的交点到三角形三个顶点的距离相等;根据勾股定理逆定理、完全平方公式的性质计算,可判断直角三角形,即可完成求解.
【详解】
当或者时,随着的增大而增大,故(1)不正确;
如果直角三角形斜边的长是斜边上的高的4倍,那么这个三角形两个锐角的度数分别是和;,故(2)正确;
∵圆的直径所对的圆周角为直角
∴斜边为的直角三角形顶点A的轨迹是以中点为圆心,长为直径的圆,故(3)正确;
三角形三边的垂直平分线的交点到三角形三个顶点的距离相等,故(4)正确;
∵
∴
∴以为三边长度的三角形,是直角三角形,故(5)错误;
故选:D.
【点睛】
本题考查了三角形、垂直平 ( http: / / www.21cnjy.com )分线、反比例函数、圆、勾股定理逆定理的知识;解题的关键是熟练掌握反比例函数、垂直平分线、圆周角、勾股定理逆定理的性质,从而完成求解.
二、填空题
1、
【分析】
如图,根据四边形CDEF为正方形,可得∠D=90°,CD=DE,从而得到CE是直径,∠ECD=45°,然后利用勾股定理,即可求解.
【详解】
解:如图,
( http: / / www.21cnjy.com / )
∵四边形CDEF为正方形,
∴∠D=90°,CD=DE,
∴CE是直径,∠ECD=45°,
根据题意得:AB=2.5, ,
∴ ,
∴ ,
即此斛底面的正方形的边长为 尺.
故答案为:
【点睛】
本题主要考查了圆内接四边形,勾股定理,熟练掌握圆内接四边形的性质,勾股定理是解题的关键.
2、40°
【分析】
由直径所对的圆周角是直角和同弧所对的圆周角相等得∠CDB的度数.
【详解】
解:连接AC,
( http: / / www.21cnjy.com / )
∵由AB是⊙O的直径,得∠ACB=90°,
∴∠CAB=90° ∠ABT=40°,
∴∠CDB=∠CAB=40°,
故答案为:40°
【点睛】
本题考查了圆周角定理,熟练掌握运用同弧所对的圆周角相等解答是关键.
3、32
【分析】
根据圆内接四边形的性质得出∠ADB+∠ACB=180°,求出∠ADB=64°,根据C是弧AB的中点求出,根据圆周角定理得出∠BDC=∠ADC=ADB,再求出答案即可.
【详解】
解:∵A、C、B、D四点共圆,
∴∠ADB+∠ACB=180°,
∵∠ACB=116°,
∴∠ADB=180°﹣116°=64°,
∵C是弧AB的中点,
∴,
∴∠BDC=∠ADC=ADB=32°,
故答案为:32.
【点睛】
本题考查四点共圆性质,圆周角与弧的关系,掌握四点共圆性质,圆周角与弧的关系是解题关键.
4、1
【分析】
以AB为直径作圆,当CF与圆相切时,AF最大.根据切线长定理转化线段AF+BC=CF,在Rt△DFC利用勾股定理求解.
【详解】
解:以AB为直径作圆,因为∠AGB=90°,所以G点在圆上.
( http: / / www.21cnjy.com / )
当CF与圆相切时,AF最大.
此时FA=FG,BC=CG.
设AF=x,则DF=4 x,FC=4+x,
在Rt△DFC中,利用勾股定理可得:
42+(4 x)2=(4+x)2,
解得x=1.
故答案为:1.
【点睛】
本题主要考查正方形的性质、圆中切线长定理以及勾股定理,熟练掌握相关性质定理是解本题的关键.
5、在⊙A上
【分析】
先根据两点间的距离公式计算出OA,然后根据点与圆的位置关系的判定方法判断点O与⊙A的位置关系.
【详解】
解:∵点A的坐标为(4,3),
∴OA==5,
∵半径为5,
∴OA=r,
∴点O在⊙A上.
故答案为:在⊙A上.
【点睛】
本题考查了点与圆的位置关系:点与圆的 ( http: / / www.21cnjy.com )位置关系有3种.设⊙O的半径为r,点P到圆心的距离OP=d,当点P在圆外 d>r;当点P在圆上 d=r;当点P在圆内 d<r.www.21-cn-jy.com
三、解答题
1、(1)见解析;(2);(3).
【分析】
(1)通过已知条件可知,,再通过同角的补交相等证得,即可得到答案;
(2)利用,得,再通过OA=OC,得;
(3)现在中,利用勾股定理求得半径r=2,再通过,得,即可求得,那么,即可求解.
【详解】
解:(1)如图,连接BF
( http: / / www.21cnjy.com / )
∵AD⊥m
∴
∵AB是⊙O的直径
∴
∴
∵,
∴
∴∠DAE=∠BAF
(2)连接OC
( http: / / www.21cnjy.com / )
∵直线m与⊙O相切于点C
∴
∵AD⊥m
∴
∴
∵OA=OC
∴
(3)连接OC
( http: / / www.21cnjy.com / )
∵直线m与⊙O相切于点C
∴
设半径OC=OB=r
在中,则:
∴
解得:r=2,即OC=r=2
∴
∴
∴
∴.
【点睛】
本题考查了圆切线、内接四边形的性质,以及解直角三角形的应用,扇形面积求法,解答此题的关键是掌握圆的性质.21教育名师原创作品
2、(1)① 2;② ;(2)t的值为3或;(3)π
【分析】
(1)①根据定义解答即可;②分别找出的最大值,再根据定义判断即可;
(2) 如图所示,正方形ABCD上的任意两点间距离的最大值为.若点E(t,3)是正方形ABCD的“倍点”,则点E到ABCD上的点的最大距离恰好为. 分, 和
分别讨论即可求解;
(3)分线段MN在内部和在外部两种情况讨论即可.
【详解】
(1)①圆上两点之间的最大距离是直径2,根据定义可知d= 2,
故答案为:2;
②由图可知,故不是图形W的“倍点”; ,故不是图形W的“倍点”;,当Q(1,0)时,=2d,故P为图形W的“倍点”;21世纪教育网版权所有
故答案为:;
(2)如图所示,正方形ABCD上的任意两点间距离的最大值为.
( http: / / www.21cnjy.com / )
依题意,若点E(t,3)是正方形ABCD的“倍点”,则点E到ABCD上的点的最大距离恰好为.
当时,点E到ABCD上的点的最大距离为EC的长. 取点H(1,3),则CH⊥EH且CH=4,此时可求得EH=4,从而点E的坐标为,即;
当时,点E到ABCD上的点的最大距离为ED的长.由对称性可得点E的坐标为,即.
当时,显然不符合题意.
综上,t的值为3或.
(3)MN上d=2,2d=4,
当线段MN在内部时,T组成的图形为半径为4的圆,,
当线段MN在外部时,T组成的图形为半径为8的圆,,
故点T所构成的图形的面积为或.
【点睛】
此题考查考查了一次函数的性质,图形上两点间的“极大距离”等知识,解题的关键是理解题意,学会寻找特殊位置解决数学问题,属于中考压轴题.
3、
(1)证明见解析;
(2).
【分析】
(1)首先证明,进而得出,再利用等腰三角形的性质得出,即可得出答案;
(2)首先证明,进而得出,以及,进而求出的长即可得出答案.
(1)
证明:如图2,在上截取,连接,,和.
( http: / / www.21cnjy.com / )
是的中点,
.
在和中
,
,
,
又,
,
;
(2)
解:如图3,截取,连接,,,
( http: / / www.21cnjy.com / )
由题意可得:,
∵
∴,
在和中
,
,
,
,
,则,
,
,
∵,
∴
则
故答案为:.
【点睛】
此题主要考查了圆与三角形综合,涉及了圆周 ( http: / / www.21cnjy.com )角定理、全等三角形的判定与性质以及等腰三角形以及等边三角形的性质,正确作出辅助线利用全等三角形的判定与性质解题是解题关键.
4、(1)见解析;(2)3π﹣.
【分析】
(1)先由圆周角定理得∠ACB=90° ( http: / / www.21cnjy.com ),则∠BAC+∠B=90°.再由平行线的性质得∠AOP=∠B,然后证∠P+∠AOP=90°,则∠PAO=90°,即可得证;【来源:21cnj*y.co*m】
(2)先证△OAP≌△BCA(AAS),得BC=OA=AB=3,再由扇形面积减去三角形面积即可解决问题.
【详解】
(1)证明:∵AB是⊙O的直径,
∴∠ACB=90°,
∴∠BAC+∠B=90°,
又∵OP∥BC,
∴∠AOP=∠B,
∴∠BAC+∠AOP=90°,
∵∠P=∠BAC,
∴∠P+∠AOP=90°,
∴∠PAO=90°,
∴PA⊥OA,
∵OA是的⊙O的半径,
∴PA为⊙O的切线;
(2)解:如图,连接OC,
( http: / / www.21cnjy.com / )
由(1)得:∠PAO=∠ACB=90°,
在△OAP和△BCA中,
,
∴△OAP≌△BCA(AAS),
∴OP=AB=6,BC=OA=OC=AB=3,
∴△OBC是等边三角形,
∴∠COB=60°,
∴∠AOC=120°,
∴S扇形AOC==3π,
∵OA=OC,
∴∠OAC=30°,
∴OH=OA=,
∴AH=,
∴AC=2AH=3,
∴S△AOC=AC OH=3×=,
∴图中阴影部分面积=S扇形AOC﹣S△AOC=3π﹣.
【点睛】
本题考查了切线的证明和扇形面积的计算,解题关键是熟练掌握切线证明方法和扇形面积公式.
5、(1)见解析;(2)
【分析】
(1)连接OC.根据半径相等,利用切线的性质和等角的余角相等证得∠ECF=∠EFC,即可得到结论;
(2)设BF=BE=x,在Rt△OCE中,利用勾股定理可求得x=2,再在Rt△ODF中,利用勾股定理即可求解.21cnjy.com
【详解】
(1)证明:如图,连接OC.
( http: / / www.21cnjy.com / )
∵CE切⊙O于点C,
∴OC⊥CE,
∴∠OCF+∠ECF=90°,
∵OD⊥AB,
∴∠D+∠DFO=90°,
∵OC=OD,
∴∠D=∠OCD,
∴∠ECF=∠OFD
又∵∠OFD=∠EFC
∴∠ECF=∠EFC,
∴EC=EF;
(2)解: ∵BF=BE,
设BF=BE=x,则EC=EF=2x,OE=3+x,
在Rt△OCE中,OC2+CE2=OE2,
∴32+(2x)2=(3+x)2,
解得x1=0(舍),x2=2,
∴OF=OB-FB=1,
在Rt△ODF中,.
【点睛】
本题考查了切线的性质,勾股定理,解一元二次方程等知识,解题的关键是灵活运用所学知识解决问题.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
九年级数学第二学期第二十七章圆与正多边形必考点解析
考试时间:90分钟;命题人:数学教研组
考生注意:
1、本卷分第I卷(选择题)和第Ⅱ卷(非选择题)两部分,满分100分,考试时间90分钟
2、答卷前,考生务必用0.5毫米黑色签字笔将自己的姓名、班级填写在试卷规定位置上
3、答案必须写在试卷各个 ( http: / / www.21cnjy.com )题目指定区域内相应的位置,如需改动,先划掉原来的答案,然后再写上新的答案;不准使用涂改液、胶带纸、修正带,不按以上要求作答的答案无效。21·世纪*教育网
第I卷(选择题 30分)
一、单选题(10小题,每小题3分,共计30分)
1、如图,四边形ABCD内接于,若,则的度数为( )
( http: / / www.21cnjy.com / )
A.50° B.100° C.130° D.150°
2、如图,点A、B、C在⊙O上,∠BAC=56°,则∠BOC的度数为( )
( http: / / www.21cnjy.com / )
A.28° B.102° C.112° D.128°
3、如图,正的边长为,边长为的正的顶点R与点A重合,点P,Q分别在AC,AB上,将沿着边AB,BC,CA连续翻转(如图所示),直至点P第一次回到原来的位置,则点P运动路径的长为( )2-1-c-n-j-y
( http: / / www.21cnjy.com / )
A. B. C. D.
4、如图,在中,,,.将绕点按逆时针方向旋转后得到,则图中阴影部分面积为( )【出处:21教育名师】
( http: / / www.21cnjy.com / )
A. B. C. D.
5、下列说法正确的个数有( )
①方程的两个实数根的和等于1;
②半圆是弧;
③正八边形是中心对称图形;
④“抛掷3枚质地均匀的硬币全部正面朝上”是随机事件;
⑤如果反比例函数的图象经过点,则这个函数图象位于第二、四象限.
A.2个 B.3个 C.4个 D.5个
6、已知正三角形外接圆半径为,这个正三角形的边长是( )
A. B. C. D.
7、如图,小王将一长为4,宽为 ( http: / / www.21cnjy.com )3的长方形木板放在桌面上按顺时针方向做无滑动的翻滚,当第二次翻滚时被桌面上一小木块挡住,此时木板与桌面成30°角,则点A运动到A2时的路径长为( )
( http: / / www.21cnjy.com / )
A.10 B.4π C. D.
8、如图,正方形ABCD的边长为8,若经过C,D两点的⊙O与直线AB相切,则⊙O的半径为( )
( http: / / www.21cnjy.com / )
A.4.8 B.5 C.4 D.4
9、如图,Rt△ABC中,∠A=90 ( http: / / www.21cnjy.com )°,∠B=30°,AC=1,将Rt△ABC延直线l由图1的位置按顺时针方向向右作无滑动滚动,当A第一次滚动到图2位置时,顶点A所经过的路径的长为( )
( http: / / www.21cnjy.com / )
A. B. C. D.(2+)π
10、下列叙述正确的有( )个.
(1)随着的增大而增大;
(2)如果直角三角形斜边的长是斜边上的高的4倍,那么这个三角形两个锐角的度数分别是和;
(3)斜边为的直角三角形顶点的轨迹是以中点为圆心,长为直径的圆;
(4)三角形三边的垂直平分线的交点到三角形三个顶点的距离相等;
(5)以为三边长度的三角形,不是直角三角形.
A.0 B.1 C.2 D.3
第Ⅱ卷(非选择题 70分)
二、填空题(5小题,每小题4分,共计20分)
1、斛是中国古代的一种量 ( http: / / www.21cnjy.com )器.据《汉书 .律历志》记载:“斛底,方而圜(huán)其外,旁有庣(tiāo)焉”.意思是说:“斛的底面为:正方形外接一个圆,此圆外是一个同心圆” . 如图所示,
问题:现有一斛,其底面的 ( http: / / www.21cnjy.com )外圆直径为两尺五寸(即2.5尺),“庣旁”为两寸五分(即两同心圆的外圆与内圆的半径之差为0.25尺),则此斛底面的正方形的边长为________尺.
( http: / / www.21cnjy.com / )
2、如图,AB是⊙O的直径,AT是⊙O的切 ( http: / / www.21cnjy.com )线,∠ABT=50°,BT交⊙O于点C,点E是AB上一点,延长CE交⊙O于点D,则∠CDB=___.21教育网
( http: / / www.21cnjy.com / )
3、如图,点D是⊙O上一点,C是弧AB的中点,若∠ACB=116°,则∠BDC的度数是 _____°.
( http: / / www.21cnjy.com / )
4、如图,正方形ABCD的边长为 ( http: / / www.21cnjy.com )4,点E是CD边上一点,连接AE,过点B作BG⊥AE于点G,连接CG并延长交AD于点F,则AF的最大值是_______.2·1·c·n·j·y
( http: / / www.21cnjy.com / )
5、已知⊙A的半径为5,圆心A(4,3),坐标原点O与⊙A的位置关系是______.
三、解答题(5小题,每小题10分,共计50分)
1、已知直线m与⊙O,AB是⊙O的直径,AD⊥m于点D.
(1)如图①,当直线m与⊙O相交于点E、F时,求证:∠DAE=∠BAF.
(2)如图②,当直线m与⊙O相切于点C时,若∠DAC=35°,求∠BAC的大小;
(3)若PC=2,PB=2,求阴影部分的面积(结果保留π).
( http: / / www.21cnjy.com / )
2、在平面直角坐标系xOy中,图形W ( http: / / www.21cnjy.com )上任意两点间的距离有最大值,将这个最大值记为d.对点P及图形W给出如下定义:点Q为图形W上任意一点,若P,Q两点间的距离有最大值,且最大值恰好为2d,则称点P为图形W的“倍点”.【版权所有:21教育】
(1)如图1,图形W是半径为1的⊙O.
①图形W上任意两点间的距离的最大值d为_________;
②在点(0,2) ,(3,3),(,0)中,⊙O的“倍点”是________;
(2)如图2,图形W是中心在原点的正方形ABCD,已知点A(,1),若点E(,3) 是正方形ABCD的“倍点”,求的值;
(3)图形W是长为2的线段MN,T为MN的中点,若在半径为6的⊙O上存在MN的“倍点”,直接写出满足条件的点T所构成的图形的面积.
( http: / / www.21cnjy.com / )
3、请阅读下列材料,并完成相应的任务:
阿基米德是有史以来最伟大的数学家之一,他与牛顿、高斯并称为三大数21世纪教育网子.阿拉伯Al-Binmi (973-1050 年)的译文中保存了阿基米德折弦定理的内容,苏联在1964年根据Al-Binmi详本出版了俄文版《阿基米德全集》.第一题就是阿基米德折弦定理.阿基米德折弦定理:如图1,和是的两条弦(即折线是圆的一条折弦),, 是的中点,则从向所作垂线的垂足是折弦的中点,即.
下面是运用“截长法”证明的部分证明过程.
证明:如图2,在上截取,连接和.
是的中点,
…
( http: / / www.21cnjy.com / )
任务:
(1)请按照上面的证明思路,写出该证明部分;
(2)填空:如图3,已知等边内接于,,为上一点,,于点,则的周长是_________.
( http: / / www.21cnjy.com / )
4、已知AB是⊙O的直径,点C是圆O上一点,点P为⊙O外一点,且OP∥BC,∠P=∠BAC.
(1)求证:PA为⊙O的切线;
(2)如果OP=AB=6,求图中阴影部分面积.
( http: / / www.21cnjy.com / )
5、如图,为⊙O的直径,半径于O,⊙O的弦与相交于点F,⊙O的切线交的延长线于点E.
( http: / / www.21cnjy.com / )
(1)求证:;
(2)若⊙O的半径长为3,且,求的长.
-参考答案-
一、单选题
1、B
【分析】
根据圆内接四边形的性质求出∠A的度数,根据圆周角定理计算即可.
【详解】
解:∵四边形ABCD内接于⊙O,
∴∠A+∠DCB=180°,
∵∠DCB=130°,
∴∠A=50°,
由圆周角定理得,=2∠A=100°,
故选:B.
【点睛】
本题考查的是圆内接四边形的性质和圆周角定理,掌握圆内接四边形的对角互补是解题的关键.
2、C
【分析】
直接由圆周角定理求解即可.
【详解】
解:∵∠A=56°,∠A与∠BOC所对的弧相同,
∴∠BOC=2∠A=112°,
故选:C.
【点睛】
此题考查了圆周角定理,熟练掌握圆周角定理是解答本题的关键,同圆或等圆中,同弧或等弧所对的圆周角等于这条弧所对的圆心角的一半.21·cn·jy·com
3、B
【分析】
从图中可以看出在AB边,翻转 ( http: / / www.21cnjy.com )的第一次是一个120度的圆心角,半径是1,第二次是以点P为圆心,所以没有路程,同理在AC和BC上也是相同的情况,由此求解即可.21*cnjy*com
【详解】
解:从图中可以看出在AB边,翻转的第一次是一个120度的圆心角,半径是1,所以弧长=,第二次是以点P为圆心,所以没有路程,在BC边上,第一次,第二次同样没有路程,AC边上也是如此,点P运动路径的长为×3=2π.21*cnjy*com
故选:B.
【点睛】
本题主要考查了等边三角形的性质,求弧长,解题的关键在于能够根据题意得到P点的运动轨迹.
4、B
【分析】
阴影部分的面积=扇形扇形,根据旋转性质以及直角三角形的性质,分别求出对应扇形的面积以及的面积,最后即可求出阴影部分的面积.
【详解】
解:由图可知:阴影部分的面积=扇形扇形,
由旋转性质可知:,,
,,
在中,,,,
,,
有勾股定理可知:,
阴影部分的面积=扇形扇形
.
故选:B.
【点睛】
本题主要是考查了旋转性质以及扇形面积公式,熟练利用旋转性质,得到对应扇形的半径和圆心角度数,利用扇形公式求解面积,这是解决本题的关键.
5、B
【分析】
根据所学知识对五个命题进行判断即可.
【详解】
1、,故方程无实数根,故本命题错误;
2、圆上任意两点间的部分叫做圆弧,半圆也是,故本命题正确;
3、八边形绕中心旋转180°以后仍然与原图重合,故本命题正确;
4、抛硬币无论抛多少,出现正反面朝上都是随机事件,故抛三枚硬币全部正面朝上也是随机事件,故本命题正确;
5、反比例函数的图象经过点 (1,2) ,则,它的函数图像位于一三象限,故本命题错误
综上所述,正确个数为3
故选B
【点睛】
本题考查一元二次函数判别式、弧的定义、中心对称图形判断、随机事件理解、反比例函数图像,掌握这些是本题关键.
6、B
【分析】
如图, 为正三角形ABC的外接圆,过点O作OD⊥AB于点D,连接OA, 再由等边三角形的性质,可得∠OAB=30°,,然后根据锐角三角函数,即可求解.www-2-1-cnjy-com
【详解】
解:如图, 为正三角形ABC的外接圆,过点O作OD⊥AB于点D,连接OA,
( http: / / www.21cnjy.com / )
根据题意得:OA= ,∠OAB=30°,,
在中,
,
∴AB=3,即这个正三角形的边长是3.
故选:B
【点睛】
本题主要考查了锐角三角函数,三角形的外接圆,熟练掌握锐角三角函数,三角形的外接圆性质是解题的关键.
7、C
【分析】
根据题意可得:第一次转动的路径是以点B为圆心,AB长为半径的弧长,此时圆心角 ,第二次转动的路径是以点C为圆心,A1C长为半径的弧长,此时圆心角 ,再由弧长公式,即可求解.
【详解】
解:如图,
( http: / / www.21cnjy.com / )
根据题意得: , ,
第一次转动的路径是以点B为圆心,AB长为半径的弧长,此时圆心角 ,
∴ ,
第二次转动的路径是以点C为圆心,A1C长为半径的弧长,此时圆心角 ,
∴ ,
∴点A运动到A2时的路径长为 .
故选:C
【点睛】
本题主要考查了求弧长,熟练掌握扇形的弧长公式是解题的关键.
8、B
【分析】
连接EO,延长EO交CD于F,连接DO,设半径为x.构建方程即可解决问题.
【详解】
解:设⊙O与AB相切于点E.连接EO,延长EO交CD于F,连接DO,
再设⊙O的半径为x.
( http: / / www.21cnjy.com / )
∵AB切⊙O于E,
∴EF⊥AB,
∵AB∥CD,
∴EF⊥CD,
∴∠OFD=90°,
在Rt△DOF中,∵∠OFD=90°,OF2+DF2=OD2,
∴(8-x)2+42= x2,
∴x=5,
∴⊙O的半径为5.
故选:B.
【点睛】
本题考查了切线的性质、正方形的性质、垂径定 ( http: / / www.21cnjy.com )理、勾股定理等知识,解题的关键是灵活运用这些知识解决问题,学会添加常用辅助线,构造直角三角形解决问题.【来源:21·世纪·教育·网】
9、C
【分析】
根据题意,画出示意图,确定出点的运动路径,再根据弧长公式即可求解.
【详解】
解:根据题意可得,Rt△ABC的运动示意图,如下:
( http: / / www.21cnjy.com / )
Rt△ABC中,∠A=90°,∠B=30°,AC=1,
∴,,,
由图形可得,点的运动路线为,先以为中心,顺时针旋转,到达点,经过的路径长为,再以为中心,顺时针旋转,到达点,经过的路径长为,
顶点A所经过的路径的长为,
故选:C
【点睛】
此题考查了旋转的性质,圆弧弧长的求解,解题的关键是根据题意确定点的运动路线.
10、D
【分析】
根据反比例函数的性质,得当或者时,随着的增大而增大;根据直径所对圆周角为直角的性质,得斜边为的直角三角形顶点的轨迹是以中点为圆心,长为直径的圆;根据垂直平分线的性质,得三角形三边的垂直平分线的交点到三角形三个顶点的距离相等;根据勾股定理逆定理、完全平方公式的性质计算,可判断直角三角形,即可完成求解.
【详解】
当或者时,随着的增大而增大,故(1)不正确;
如果直角三角形斜边的长是斜边上的高的4倍,那么这个三角形两个锐角的度数分别是和;,故(2)正确;
∵圆的直径所对的圆周角为直角
∴斜边为的直角三角形顶点A的轨迹是以中点为圆心,长为直径的圆,故(3)正确;
三角形三边的垂直平分线的交点到三角形三个顶点的距离相等,故(4)正确;
∵
∴
∴以为三边长度的三角形,是直角三角形,故(5)错误;
故选:D.
【点睛】
本题考查了三角形、垂直平 ( http: / / www.21cnjy.com )分线、反比例函数、圆、勾股定理逆定理的知识;解题的关键是熟练掌握反比例函数、垂直平分线、圆周角、勾股定理逆定理的性质,从而完成求解.
二、填空题
1、
【分析】
如图,根据四边形CDEF为正方形,可得∠D=90°,CD=DE,从而得到CE是直径,∠ECD=45°,然后利用勾股定理,即可求解.
【详解】
解:如图,
( http: / / www.21cnjy.com / )
∵四边形CDEF为正方形,
∴∠D=90°,CD=DE,
∴CE是直径,∠ECD=45°,
根据题意得:AB=2.5, ,
∴ ,
∴ ,
即此斛底面的正方形的边长为 尺.
故答案为:
【点睛】
本题主要考查了圆内接四边形,勾股定理,熟练掌握圆内接四边形的性质,勾股定理是解题的关键.
2、40°
【分析】
由直径所对的圆周角是直角和同弧所对的圆周角相等得∠CDB的度数.
【详解】
解:连接AC,
( http: / / www.21cnjy.com / )
∵由AB是⊙O的直径,得∠ACB=90°,
∴∠CAB=90° ∠ABT=40°,
∴∠CDB=∠CAB=40°,
故答案为:40°
【点睛】
本题考查了圆周角定理,熟练掌握运用同弧所对的圆周角相等解答是关键.
3、32
【分析】
根据圆内接四边形的性质得出∠ADB+∠ACB=180°,求出∠ADB=64°,根据C是弧AB的中点求出,根据圆周角定理得出∠BDC=∠ADC=ADB,再求出答案即可.
【详解】
解:∵A、C、B、D四点共圆,
∴∠ADB+∠ACB=180°,
∵∠ACB=116°,
∴∠ADB=180°﹣116°=64°,
∵C是弧AB的中点,
∴,
∴∠BDC=∠ADC=ADB=32°,
故答案为:32.
【点睛】
本题考查四点共圆性质,圆周角与弧的关系,掌握四点共圆性质,圆周角与弧的关系是解题关键.
4、1
【分析】
以AB为直径作圆,当CF与圆相切时,AF最大.根据切线长定理转化线段AF+BC=CF,在Rt△DFC利用勾股定理求解.
【详解】
解:以AB为直径作圆,因为∠AGB=90°,所以G点在圆上.
( http: / / www.21cnjy.com / )
当CF与圆相切时,AF最大.
此时FA=FG,BC=CG.
设AF=x,则DF=4 x,FC=4+x,
在Rt△DFC中,利用勾股定理可得:
42+(4 x)2=(4+x)2,
解得x=1.
故答案为:1.
【点睛】
本题主要考查正方形的性质、圆中切线长定理以及勾股定理,熟练掌握相关性质定理是解本题的关键.
5、在⊙A上
【分析】
先根据两点间的距离公式计算出OA,然后根据点与圆的位置关系的判定方法判断点O与⊙A的位置关系.
【详解】
解:∵点A的坐标为(4,3),
∴OA==5,
∵半径为5,
∴OA=r,
∴点O在⊙A上.
故答案为:在⊙A上.
【点睛】
本题考查了点与圆的位置关系:点与圆的 ( http: / / www.21cnjy.com )位置关系有3种.设⊙O的半径为r,点P到圆心的距离OP=d,当点P在圆外 d>r;当点P在圆上 d=r;当点P在圆内 d<r.www.21-cn-jy.com
三、解答题
1、(1)见解析;(2);(3).
【分析】
(1)通过已知条件可知,,再通过同角的补交相等证得,即可得到答案;
(2)利用,得,再通过OA=OC,得;
(3)现在中,利用勾股定理求得半径r=2,再通过,得,即可求得,那么,即可求解.
【详解】
解:(1)如图,连接BF
( http: / / www.21cnjy.com / )
∵AD⊥m
∴
∵AB是⊙O的直径
∴
∴
∵,
∴
∴∠DAE=∠BAF
(2)连接OC
( http: / / www.21cnjy.com / )
∵直线m与⊙O相切于点C
∴
∵AD⊥m
∴
∴
∵OA=OC
∴
(3)连接OC
( http: / / www.21cnjy.com / )
∵直线m与⊙O相切于点C
∴
设半径OC=OB=r
在中,则:
∴
解得:r=2,即OC=r=2
∴
∴
∴
∴.
【点睛】
本题考查了圆切线、内接四边形的性质,以及解直角三角形的应用,扇形面积求法,解答此题的关键是掌握圆的性质.21教育名师原创作品
2、(1)① 2;② ;(2)t的值为3或;(3)π
【分析】
(1)①根据定义解答即可;②分别找出的最大值,再根据定义判断即可;
(2) 如图所示,正方形ABCD上的任意两点间距离的最大值为.若点E(t,3)是正方形ABCD的“倍点”,则点E到ABCD上的点的最大距离恰好为. 分, 和
分别讨论即可求解;
(3)分线段MN在内部和在外部两种情况讨论即可.
【详解】
(1)①圆上两点之间的最大距离是直径2,根据定义可知d= 2,
故答案为:2;
②由图可知,故不是图形W的“倍点”; ,故不是图形W的“倍点”;,当Q(1,0)时,=2d,故P为图形W的“倍点”;21世纪教育网版权所有
故答案为:;
(2)如图所示,正方形ABCD上的任意两点间距离的最大值为.
( http: / / www.21cnjy.com / )
依题意,若点E(t,3)是正方形ABCD的“倍点”,则点E到ABCD上的点的最大距离恰好为.
当时,点E到ABCD上的点的最大距离为EC的长. 取点H(1,3),则CH⊥EH且CH=4,此时可求得EH=4,从而点E的坐标为,即;
当时,点E到ABCD上的点的最大距离为ED的长.由对称性可得点E的坐标为,即.
当时,显然不符合题意.
综上,t的值为3或.
(3)MN上d=2,2d=4,
当线段MN在内部时,T组成的图形为半径为4的圆,,
当线段MN在外部时,T组成的图形为半径为8的圆,,
故点T所构成的图形的面积为或.
【点睛】
此题考查考查了一次函数的性质,图形上两点间的“极大距离”等知识,解题的关键是理解题意,学会寻找特殊位置解决数学问题,属于中考压轴题.
3、
(1)证明见解析;
(2).
【分析】
(1)首先证明,进而得出,再利用等腰三角形的性质得出,即可得出答案;
(2)首先证明,进而得出,以及,进而求出的长即可得出答案.
(1)
证明:如图2,在上截取,连接,,和.
( http: / / www.21cnjy.com / )
是的中点,
.
在和中
,
,
,
又,
,
;
(2)
解:如图3,截取,连接,,,
( http: / / www.21cnjy.com / )
由题意可得:,
∵
∴,
在和中
,
,
,
,
,则,
,
,
∵,
∴
则
故答案为:.
【点睛】
此题主要考查了圆与三角形综合,涉及了圆周 ( http: / / www.21cnjy.com )角定理、全等三角形的判定与性质以及等腰三角形以及等边三角形的性质,正确作出辅助线利用全等三角形的判定与性质解题是解题关键.
4、(1)见解析;(2)3π﹣.
【分析】
(1)先由圆周角定理得∠ACB=90° ( http: / / www.21cnjy.com ),则∠BAC+∠B=90°.再由平行线的性质得∠AOP=∠B,然后证∠P+∠AOP=90°,则∠PAO=90°,即可得证;【来源:21cnj*y.co*m】
(2)先证△OAP≌△BCA(AAS),得BC=OA=AB=3,再由扇形面积减去三角形面积即可解决问题.
【详解】
(1)证明:∵AB是⊙O的直径,
∴∠ACB=90°,
∴∠BAC+∠B=90°,
又∵OP∥BC,
∴∠AOP=∠B,
∴∠BAC+∠AOP=90°,
∵∠P=∠BAC,
∴∠P+∠AOP=90°,
∴∠PAO=90°,
∴PA⊥OA,
∵OA是的⊙O的半径,
∴PA为⊙O的切线;
(2)解:如图,连接OC,
( http: / / www.21cnjy.com / )
由(1)得:∠PAO=∠ACB=90°,
在△OAP和△BCA中,
,
∴△OAP≌△BCA(AAS),
∴OP=AB=6,BC=OA=OC=AB=3,
∴△OBC是等边三角形,
∴∠COB=60°,
∴∠AOC=120°,
∴S扇形AOC==3π,
∵OA=OC,
∴∠OAC=30°,
∴OH=OA=,
∴AH=,
∴AC=2AH=3,
∴S△AOC=AC OH=3×=,
∴图中阴影部分面积=S扇形AOC﹣S△AOC=3π﹣.
【点睛】
本题考查了切线的证明和扇形面积的计算,解题关键是熟练掌握切线证明方法和扇形面积公式.
5、(1)见解析;(2)
【分析】
(1)连接OC.根据半径相等,利用切线的性质和等角的余角相等证得∠ECF=∠EFC,即可得到结论;
(2)设BF=BE=x,在Rt△OCE中,利用勾股定理可求得x=2,再在Rt△ODF中,利用勾股定理即可求解.21cnjy.com
【详解】
(1)证明:如图,连接OC.
( http: / / www.21cnjy.com / )
∵CE切⊙O于点C,
∴OC⊥CE,
∴∠OCF+∠ECF=90°,
∵OD⊥AB,
∴∠D+∠DFO=90°,
∵OC=OD,
∴∠D=∠OCD,
∴∠ECF=∠OFD
又∵∠OFD=∠EFC
∴∠ECF=∠EFC,
∴EC=EF;
(2)解: ∵BF=BE,
设BF=BE=x,则EC=EF=2x,OE=3+x,
在Rt△OCE中,OC2+CE2=OE2,
∴32+(2x)2=(3+x)2,
解得x1=0(舍),x2=2,
∴OF=OB-FB=1,
在Rt△ODF中,.
【点睛】
本题考查了切线的性质,勾股定理,解一元二次方程等知识,解题的关键是灵活运用所学知识解决问题.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
