2022-2023学年华东师大版八年级数学上册12.3乘法公式 解答题优生辅导训练(word、含答案)
文档属性
| 名称 | 2022-2023学年华东师大版八年级数学上册12.3乘法公式 解答题优生辅导训练(word、含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 178.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-20 15:34:14 | ||
图片预览

文档简介
2022-2023学年华东师大版八年级数学上册《12.3乘法公式》
解答题优生辅导训练(附答案)
1.计算:(2x﹣2)(x+1)﹣(x﹣1)2﹣(x+1)2
2.已知x+y=3,xy=2,求下列各式的值.
(1)x2+y2;
(2)(x﹣1)(y﹣1).
3.利用乘法公式解决下列问题:
(1)若x﹣y=8,xy=40.则x2+y2= ;
(2)已知,若x满足(25﹣x)(x﹣10)=﹣15,求(25﹣x)2+(x﹣10)2值.
4.已知多项式A=(x+2)2+(x+2)(1﹣x)﹣3.
(1)化简多项式A;
(2)若(x+1)2=5,求A的值.
5.阅读下列文字,寻找规律,解答下列各小题.
已知x≠1,计算:
(1﹣x)(1+x)=1﹣x2
(1﹣x)(1+x+x2)=1﹣x3
(1﹣x)(1+x+x2+x3)=1﹣x4
(1﹣x)(1+x+x2+x3+x4)=1﹣x5
(1)观察上式计算:(1﹣x)(1+x+x2+…+xm)= .
(2)计算:
①(1﹣2)(1+2+22+23+…+22022);
②2+22+23+24+…+2m.
6.阅读、理解、应用.
例:计算:20223﹣2021×2022×2023.
解:设2022=x,则原式=x3﹣(x﹣1) x (x+1)=x3﹣x(x2﹣1)=x=2022.
请你利用上述方法解答下列问题:
(1)计算:1232﹣124×122;
(2)若M=123456789×123456786,N=123456788×123456787,请比较M,N的大小;
(3)计算:
7.观察下列各式:
(a+1)(a2﹣a+1)=a3+1;
(a﹣2)(a2+2a+4)=a3﹣8;
(3a﹣2)(9a2+6a+4)=27a3﹣8.
(1)请你按照以上各式的运算规律,填空.
①(x﹣3)(x2+3x+9)= ;
②(2x+1)( )=8x3+1;
③( )(x2+xy+y2)=x3﹣y3.
(2)应用规律计算:(a2﹣b2)(a2+ab+b2)(a2﹣ab+b2).
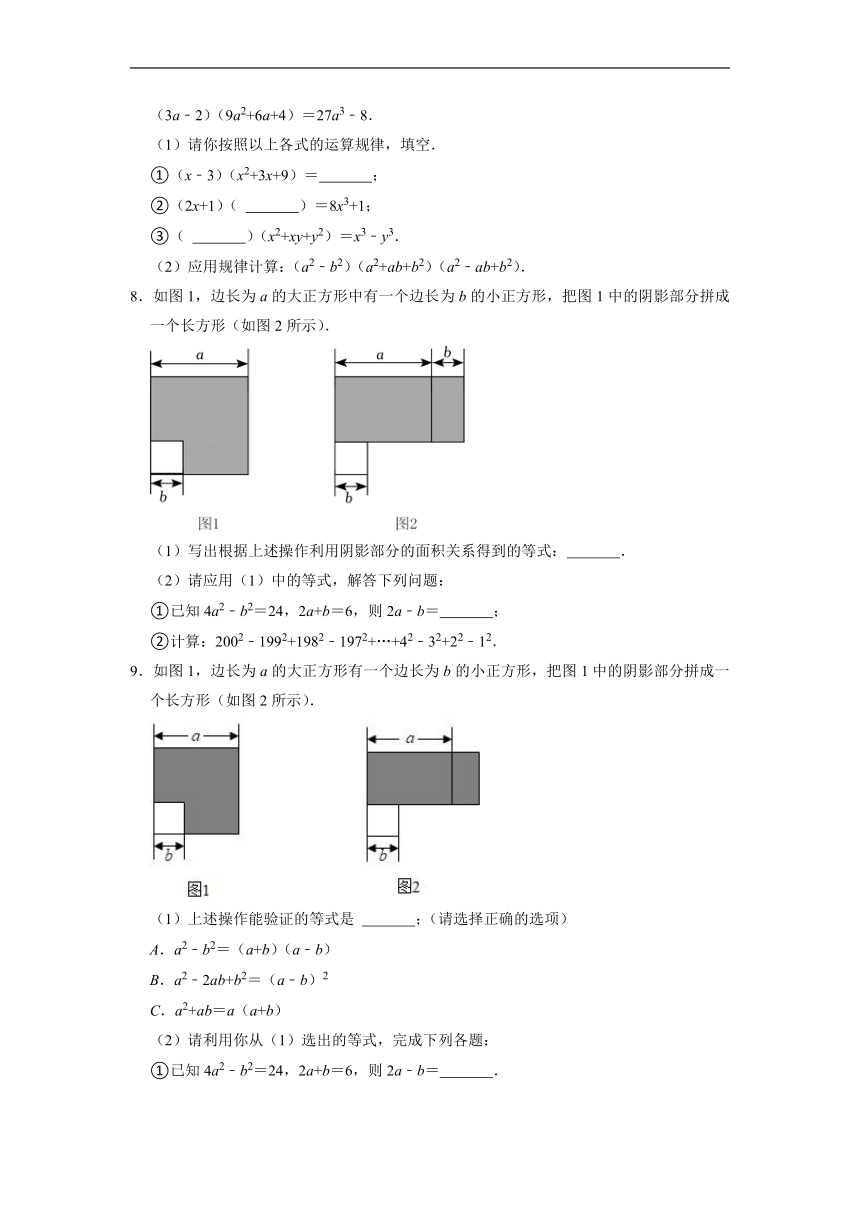
8.如图1,边长为a的大正方形中有一个边长为b的小正方形,把图1中的阴影部分拼成一个长方形(如图2所示).
(1)写出根据上述操作利用阴影部分的面积关系得到的等式: .
(2)请应用(1)中的等式,解答下列问题:
①已知4a2﹣b2=24,2a+b=6,则2a﹣b= ;
②计算:2002﹣1992+1982﹣1972+…+42﹣32+22﹣12.
9.如图1,边长为a的大正方形有一个边长为b的小正方形,把图1中的阴影部分拼成一个长方形(如图2所示).
(1)上述操作能验证的等式是 ;(请选择正确的选项)
A.a2﹣b2=(a+b)(a﹣b)
B.a2﹣2ab+b2=(a﹣b)2
C.a2+ab=a(a+b)
(2)请利用你从(1)选出的等式,完成下列各题:
①已知4a2﹣b2=24,2a+b=6,则2a﹣b= .
②计算:(1﹣)(1﹣)(1﹣)…(1﹣)(1﹣).
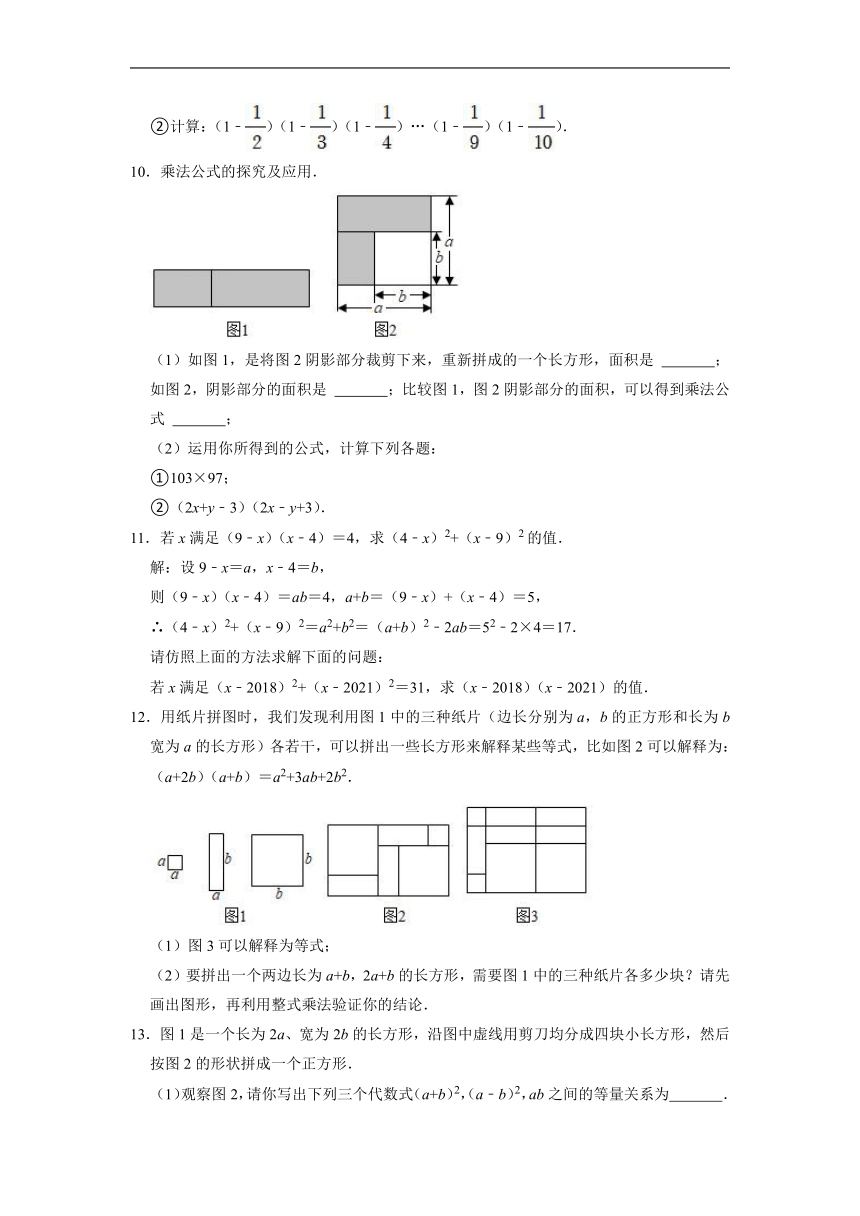
10.乘法公式的探究及应用.
(1)如图1,是将图2阴影部分裁剪下来,重新拼成的一个长方形,面积是 ;如图2,阴影部分的面积是 ;比较图1,图2阴影部分的面积,可以得到乘法公式 ;
(2)运用你所得到的公式,计算下列各题:
①103×97;
②(2x+y﹣3)(2x﹣y+3).
11.若x满足(9﹣x)(x﹣4)=4,求(4﹣x)2+(x﹣9)2的值.
解:设9﹣x=a,x﹣4=b,
则(9﹣x)(x﹣4)=ab=4,a+b=(9﹣x)+(x﹣4)=5,
∴(4﹣x)2+(x﹣9)2=a2+b2=(a+b)2﹣2ab=52﹣2×4=17.
请仿照上面的方法求解下面的问题:
若x满足(x﹣2018)2+(x﹣2021)2=31,求(x﹣2018)(x﹣2021)的值.
12.用纸片拼图时,我们发现利用图1中的三种纸片(边长分别为a,b的正方形和长为b宽为a的长方形)各若干,可以拼出一些长方形来解释某些等式,比如图2可以解释为:(a+2b)(a+b)=a2+3ab+2b2.
(1)图3可以解释为等式;
(2)要拼出一个两边长为a+b,2a+b的长方形,需要图1中的三种纸片各多少块?请先画出图形,再利用整式乘法验证你的结论.
13.图1是一个长为2a、宽为2b的长方形,沿图中虚线用剪刀均分成四块小长方形,然后按图2的形状拼成一个正方形.
(1)观察图2,请你写出下列三个代数式(a+b)2,(a﹣b)2,ab之间的等量关系为 .
(2)运用你所得到的公式,计算:若m、n为实数,且mn=﹣3,m﹣n=4,试求m+n的值.
(3)如图3,点C是线段AB上的一点,以AC、BC为边向两边作正方形,设AB=8,两正方形的面积和S1+S2=26,求图中阴影部分面积.
14.阅读理解:
若x满足(80﹣x)(x﹣60)=30,求(80﹣x)2+(x﹣60)2的值.
解:设80﹣x=a,x﹣60=b,则(80﹣x)(x﹣60)=ab=30,a+b=(80﹣x)+(x﹣60)=20,
∴(80﹣x)2+(x﹣60)2=a2+b2=(a+b)2﹣2ab=202﹣2×30=340.
解决问题
(1)若x满足(20﹣x)(x﹣10)=﹣10,求(20﹣x)2+(x﹣10)2的值;
(2)若x满足(2022﹣x)2+(2020﹣x)2=4048,求(2022﹣x)(2020﹣x)的值.
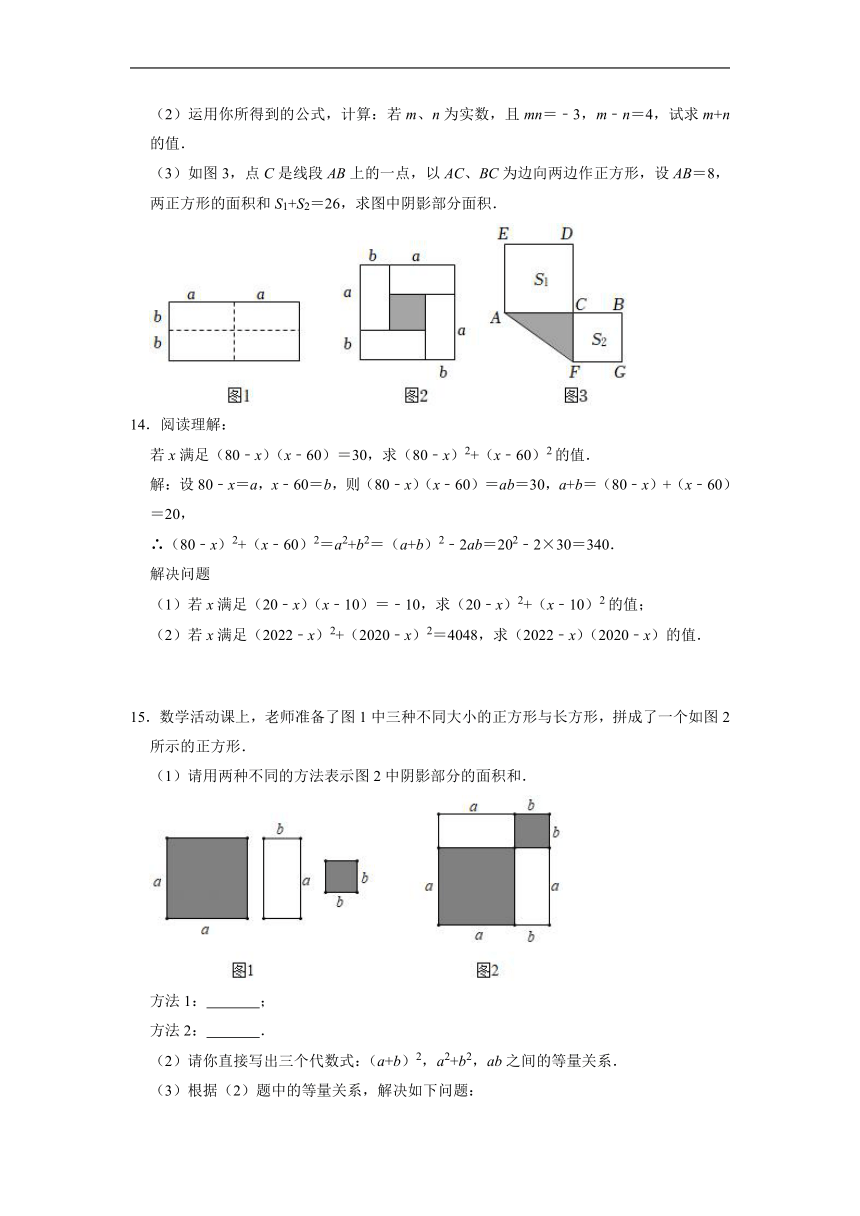
15.数学活动课上,老师准备了图1中三种不同大小的正方形与长方形,拼成了一个如图2所示的正方形.
(1)请用两种不同的方法表示图2中阴影部分的面积和.
方法1: ;
方法2: .
(2)请你直接写出三个代数式:(a+b)2,a2+b2,ab之间的等量关系.
(3)根据(2)题中的等量关系,解决如下问题:
①已知m+n=5,m2+n2=20,求mn和(m﹣n)2的值;
②已知(x﹣2021)2+(x﹣2023)2=34,求(x﹣2022)2的值.
16.数学活动课上,张老师准备了若干个如图①的三种纸片,A种纸片是边长为a的正方形,B种纸片是边长为b的正方形,C种纸片是长为b,宽为a的长方形,并用A种纸片一张,B种纸片一张,C种纸片两张拼成如图②的大正方形.
(1)观察图②,写出代数式(a+b)2,a2+b2,ab之间的等量关系是 ;
(2)根据(1)中的等量关系,解决下列问题;
①已知a+b=4,a2+b2=10,求ab的值;
②已知(x﹣2021)2+(x﹣2019)2=130,直接写出x﹣2020的值.
17.如图1是一个长为4a,宽为b的长方形,沿图中虚线用剪刀平均分成四块小长方形,然后用四块小长方形拼成如图2的正方形.
(1)由图2可以直接写出(a+b)2,(a﹣b)2,ab之间的一个等量关系是 .
(2)根据(1)中的结论,解决下列问题:3x+4y=10,xy=2,求3x﹣4y的值;
(3)两个正方形ABCD,AEFG如图3摆放,边长分别为x,y.若x2+y2=34,BE=2,求图中阴影部分面积和.
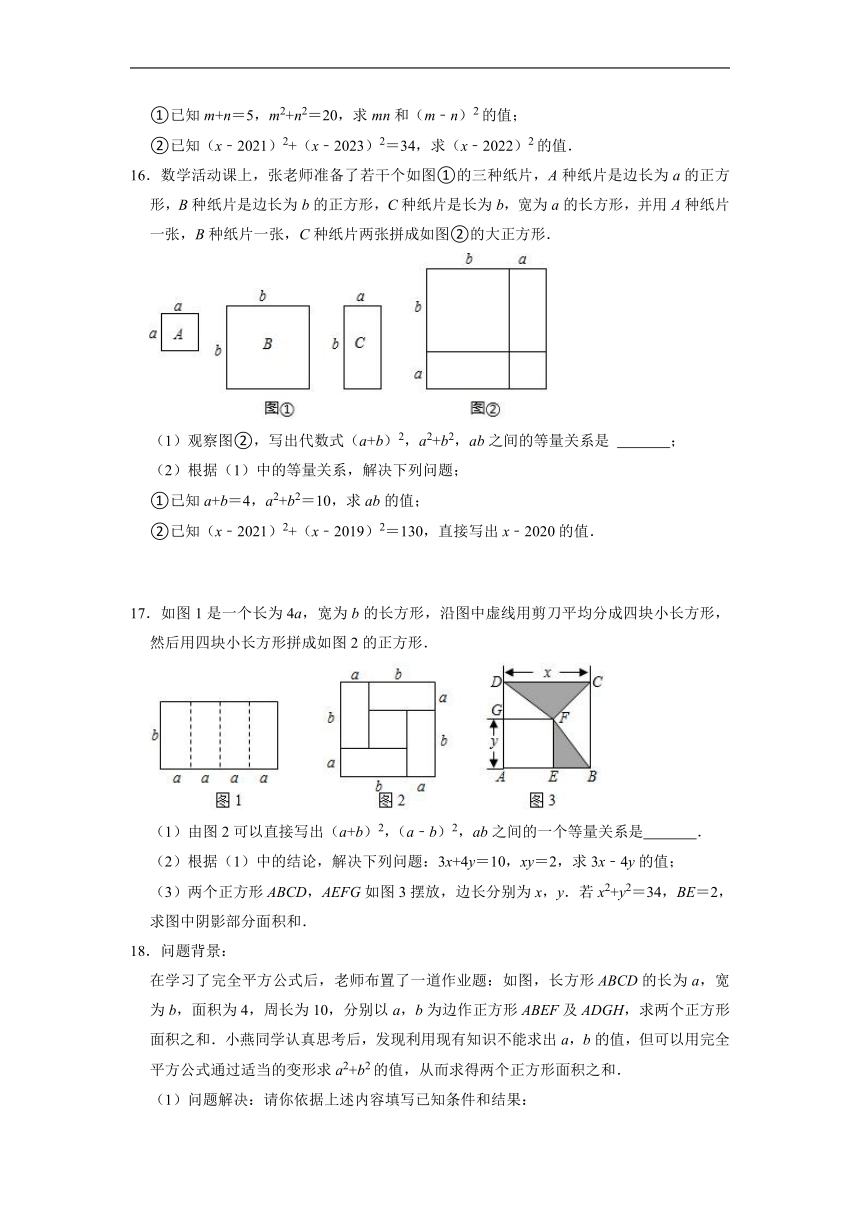
18.问题背景:
在学习了完全平方公式后,老师布置了一道作业题:如图,长方形ABCD的长为a,宽为b,面积为4,周长为10,分别以a,b为边作正方形ABEF及ADGH,求两个正方形面积之和.小燕同学认真思考后,发现利用现有知识不能求出a,b的值,但可以用完全平方公式通过适当的变形求a2+b2的值,从而求得两个正方形面积之和.
(1)问题解决:请你依据上述内容填写已知条件和结果:
a+b= ,ab= ,a2+b2= .
(2)已知x+y=7,xy=10,求(x﹣y)2的值.
19.阅读理解:
若x满足(30﹣x)(x﹣10)=160,求(30﹣x)2+(x﹣10)2的值.
解:设30﹣x=a,x﹣10=b,则(30﹣x)(x﹣10)=ab=160,a+b=(30﹣x)+(x﹣10)=20,(30﹣x)2+(x﹣10)2=a2+b2=(a+b)2﹣2ab=202﹣2×160=80
解决问题:
(1)若x满足(2020﹣x)(x﹣2016)=2.则(2020﹣x)2+(x﹣2016)2= ;
(2)若x满足(2021﹣x)2+(x﹣2018)2=2020,求(2021﹣x)(x﹣2018)的值;
(3)如图,在长方形ABCD中,AB=20,BC=12,点E.F是BC、CD上的点,且BE=DF=x,分别以FC、CE为边在长方形ABCD外侧作正方形CFGH和CEMN,若长方形CEPF的面积为160平方单位,则图中阴影部分的面积和为 平方单位.
20.若x满足(x﹣4)(x﹣9)=6,求(x﹣4)2+(x﹣9)2的值.阅读下面求解的方法:
解:设(x﹣4)=a,(x﹣9)=b,则ab=(x﹣4)(x﹣9)=6,a﹣b=(x﹣4)﹣(x﹣9)=5
∴(x﹣4)2+(x﹣9)2=a2+b2=(a﹣b)2+2ab=52+2×6=37.
请仿照上面的方法求解下面的问题:
(1)若x满足(x﹣2)(x﹣5)=10,求(x﹣2)2+(x﹣5)2的值;
(2)如图,正方形ABCD中,E、F分别是AD、DC上的点,且AE=1,CF=3,长方形EMFD的面积是15,分别以MF、DF为边作正方形,若AD=x,则
①DE= ,DF= (用含x的代数式表示);
②直接写出图中阴影部分的面积.
参考答案
1.解:原式=2x2+2x﹣2x﹣2﹣(x2﹣2x+1)﹣(x2+2x+1)
=2x2+2x﹣2x﹣2﹣x2+2x﹣1﹣x2﹣2x﹣1
=﹣4.
2.解:(1)将x+y=3两边平方得:
(x+y)2=x2+2xy+y2=9,
将xy=2代入得:
x2+y2=5;
(2)原式=xy﹣(x+y)+1
=2﹣3+1
=0.
3.解:(1)∵x2+y2=(x﹣y)2+2xy,
把x﹣y=8,xy=40,代入上式,得x2+y2=82+2×40=144.
故答案是:144;
(2)设25﹣x=a,x﹣10=b,
由(a+b)2=a2+2ab+b2进行变形得,
a2+b2=(a+b)2﹣2ab,
∴(25﹣x)2+(x﹣10)2
=[(25﹣x)+(x﹣10)]2﹣2(25﹣x)(x﹣10)
=152﹣2×(﹣15)
=225+30
=255.
4.解:(1)A=x2+4x+4+x+2﹣x2﹣2x﹣3=3x+3;
(2)∵(x+1)2=5,
∴x+1=±,
则A=3x+3=3(x+1)=±3 .
5.解:(1)观察上面的式子得到原式=1﹣xm+1,
故答案为:1﹣xm+1;
(2)①当x=2时,原式=1﹣22023;
②当x=2时,(1﹣2)(1+2+22+23+…+2m)=1﹣2m+1,
∴1+2+22+23+…+2m=2m+1﹣1,
∴原式=2m+1﹣2.
6.解:(1)设123=x,
∴1232﹣124×122
=x2﹣(x+1)(x﹣1)
=x2﹣x2+1
=1;
(2)设123456786=x,
∴M=123456789×123456786
=(x+3) x
=x2+3x,
N=123456788×123456787
=(x+2)(x+1)
=x2+3x+2,
∴M<N;
(3)设++...+=x,
=(x+)(1+x)﹣(1+x+) x
=x+x2++x﹣x﹣x2﹣x
=.
7.解:(1)①(x﹣3)(x2+3x+9)=x3﹣27;
②(2x+1)(4x2﹣2x+1)=8x3+1;
③(x﹣y)(x2+xy+y2)=x3﹣y3.
故答案为:①x3﹣27;②4x2﹣2x+1;③x﹣y;
(2)(a2﹣b2)(a2+ab+b2)(a2﹣ab+b2)
=[(a+b)(a2﹣ab+b2)][(a﹣b)(a2+ab+b2)]
=(a3+b3)(a3﹣b3)
=a6﹣b6.
8.解:(1)根据上述操作利用阴影部分的面积关系得到的等式:a2﹣b2=(a+b)(a﹣b),
故答案为:a2﹣b2=(a+b)(a﹣b);
(2)①∵4a2﹣b2=24,
∴(2a+b)(2a﹣b)=24,
∵2a+b=6,
∴2a﹣b=4,
故答案为:4,
②2002﹣1992+1982﹣1972+…+42﹣32+22﹣12
=(200+199)(200﹣199)+(198+197)(198﹣197)+...+(4+3)(4﹣3)+(2+1)(2﹣1)
=200+199+198+197+...+4+3+2+1
=×(200+1)×200
=20100.
9.解:(1)图1中阴影部分的面积=a2﹣b2,图②中阴影部分的面积=(a+b)(a﹣b).
∴a2﹣b2=(a+b)(a﹣b).
故选A.
(2)①∵(2a+b)(2a﹣b)=4a2﹣b2.
∴6(2a﹣b)=24,
∴2a﹣b=24÷6=4.
故答案为:4.
②=
=
=
=.
10.解:(1)由拼图可知,图形1的长为(a+b),宽为(a﹣b),因此面积为(a+b)(a﹣b),图形2的阴影部分的面积为两个正方形的面积差,即a2﹣b2,
由图形1,图形2的面积相等可得,(a+b)(a﹣b)=a2﹣b2,
故答案为:(a+b)(a﹣b),a2﹣b2,(a+b)(a﹣b)=a2﹣b2;
(2)①103×97=(100+3)(100﹣3)
=1002﹣32
=10000﹣9
=9991;
②原式=(2x+y﹣3)[2x﹣(y﹣3)]
=(2x)2﹣(y﹣3)2
=4x2﹣(y2﹣6y+9)
=4x2﹣y2+6y﹣9.
11.解:设x﹣2018=a,x﹣2021=b,
则a2+b2=31,a﹣b=x﹣2018﹣x+2021=3,
∴a2﹣2ab+b2=(a﹣b)2=9,
∴31﹣2ab=9,
解得ab=11,
即(x﹣2018)(x﹣2021)=11.
12.解:(1)∵图3面积为(a+2b)(2a+b)=2a2+5ab+2b2,
∴图3可以解释为等式(a+2b)(2a+b)=2a2+5ab+2b2.
(2)需要边长为a的正方形2块,长为b宽为a的长方形3块,边长为b的正方形1块.如下图所示:
整式乘法验证,(a+b)(2a+b)=2a2+ab+2ab+b2=2a2+3ab+b2,
∴需要a×a的正方形2块,需要a×b的长方形3块,需要b×b的正方形1块.
13.解:(1)图2,大正方形的边长为a+b,因此面积为(a+b)2,
小正方形的边长为a﹣b,因此面积为(a﹣b)2,
每个长方形的长为a,宽为b,因此面积为ab,
由面积之间的关系可得,(a+b)2=(a﹣b)2+4ab,
故答案为:(a+b)2=(a﹣b)2+4ab;
(2)由(1)得,(m+n)2=(m﹣n)2+4mn,
即(m+n)2=42+4×(﹣3),
∴m+n=2或m+n=﹣2;
(3)设正方形ACDE的边长为a,正方形BCFG的边长为b,则S1=a2,S2=b2,
由于AB=8,两正方形的面积和S1+S2=26,
因此a+b=8,a2+b2=26,
∵(a+b)2=a2+2ab+b2,即64=26+2ab,
∴ab=19,
∴阴影部分的面积为ab=.
14.解:(1)设(20﹣x)=a,(x﹣10)=b,
则(20﹣x)(x﹣10)=ab=﹣10,a+b=(20﹣x)+(x﹣10)=10,
所以(20﹣x)2+(x﹣10)2=a2+b2=(a+b)2﹣2ab=102+2×10=120;
(2)设(2022﹣x)=a,(2020﹣x)=b,
则a﹣b=(2022﹣x)﹣(2020﹣x)=2,
因为(2022﹣x)2+(2020﹣x)2=4048,
所以(2022﹣x)2+(2020﹣x)2=a2+b2=(a﹣b)2+2ab=4048,
即22+2×(2022﹣x)(2020﹣x)=4048,
(2019﹣x)(2017﹣x)=2022.
15.解:(1)阴影两部分求和为a2+b2,用总面积减去空白部分面积为(a+b)2﹣2ab,
故答案为:a2+b2,(a+b)2﹣2ab;
(2)由题意得,a2+b2=(a+b)2﹣2ab;
(3)①由(2)题结论a2+b2=(a+b)2﹣2ab可得ab=,
∴m+n=5,m2+n2=20时,
mn=
=
=,
(m﹣n)2
=m2﹣2mn+n2;
=20﹣2×
=20﹣5
=15;
②设a=x﹣2021,b=x﹣2023,
可得a+b=(x﹣2021)+(x﹣2023)
=x﹣2021+x﹣2023
=2x﹣4044
=2(x﹣2022),
由(2)题结论a2+b2=(a+b)2﹣2ab可得,
(a+b)2=a2+2ab+b2,
又∵(a﹣b)2=[(x﹣2021)﹣(x﹣2023)]2=22=4,
且由(a﹣b)2=a2﹣2ab+b2,可得2ab=(a2+b2)﹣(a﹣b)2=(x﹣2021)2+(x﹣2023)2﹣[(x﹣2021)﹣(x﹣2023)]2=34﹣4=30,
∴(x﹣2022)2=()2====16.
16.解:(1)∵图形②是边长为(a+b)的正方形,
∴S=(a+b)2.
∵大正方形的面积由一个边长为a的正方形和一个边长为b的正方形以及两个长为b,宽为a的长方形组合而成,
∴S=a2+2ab+b2.
∴(a+b)2=a2+2ab+b2.
故答案为:(a+b)2=a2+2ab+b2.
(2)①∵a+b=4,
∴(a+b)2=16.
∴a2+2ab+b2=16.
∵a2+b2=10,
∴ab=3.
②设x﹣2020=a,则x﹣2021=a﹣1,x﹣2019=a+1.
∵(x﹣2021)2+(x﹣2019)2=130,
∴(a﹣1)2+(a+1)2=130.
∴a2﹣2a+1+a2+2a+1=130.
∴2a2=128.
∴a2=64.
即(x﹣2020)2=64.
∴x﹣2020=±8.
17.解:(1)∵大正方形的面积等于4个小长方形和小正方形面积之和,
∴(a+b)2=4ab+(b﹣a)2.
∴(a+b)2=(a﹣b)2+4ab.
故答案为:(a+b)2=(a﹣b)2+4ab.
(2)由(1)得:
(3x+4y)2=(3x﹣4y)2+4×3x×4y.
∴(3x﹣4y)2=(3x+4y)2﹣48xy
∴(3x﹣4y)2=100﹣96=4.
∴3x﹣4y=±2.
(3)∵ABCD,AEFG为正方形,边长分别为x,y.BE=2,
∴DG=BE=2,x﹣y=2.
∴(x﹣y)2=4.
∴x2﹣2xy+y2=4.
∵x2+y2=34,
∴2xy=30.
∴x2+2xy+y2=34+30,
∴(x+y)2=64.
∵x>0,y>0,
∴x+y=8.
∴=y+x=8.
18.解:(1)∵长方形ABCD的周长为10,
∴a+b=5.
∵长方形ABCD的面积为4,
∴ab=4.
∵(a+b)2=a2+2ab+b2,
∴a2+b2=(a+b)2﹣2ab=25﹣8=17.
故答案为:5,4,17.
(2)∵(x+y)2=x2+2xy+y2,(x﹣y)2=x2﹣2xy+y2,
∴(x﹣y)2=(x+y)2﹣4xy.
∴(x﹣y)2=72﹣4×10=9.
19.解:(1)设2020﹣x=a,x﹣2016=b,则(2020﹣x)(x﹣2016)=ab=2,a+b=(2020﹣x)+(x﹣2016)=4,
所以(2020﹣x)2+(x﹣2016)2=a2+b2=(a+b)2﹣2ab=42﹣2×2=12;
故答案为:12;
(2)设2021﹣x=a,x﹣2018=b,则(2021﹣x)2+(x﹣2018)2=a2+b2=2020,a+b=(2021﹣x)+(x﹣2018)=3,
所以(2021﹣x)(x﹣2018)=ab=[(a+b)2﹣(a2+b2)]=×(32﹣2020)=﹣;
答:(2021﹣x)(x﹣2018)的值为﹣;
(3)由题意得,FC=(20﹣x),EC=(12﹣x),
∵长方形CEPF的面积为160,
∴(20﹣x)(12﹣x)=160,
∴(20﹣x)(x﹣12)=﹣160,
∴阴影部分的面积为(20﹣x)2+(12﹣x)2,
设20﹣x=a,x﹣12=b,则(20﹣x)(x﹣12)=ab=﹣160,a+b=(20﹣x)+(x﹣12)=8,
所以(20﹣x)2+(x﹣12)2=(20﹣x)2+(12﹣x)2=a2+b2=(a+b)2﹣2ab=82﹣2×(﹣160)=384;
故答案为:384.
20.解:(1)设(x﹣2)=a,(x﹣5)=b,则ab=(x﹣2)(x﹣5)=10,a﹣b=(x﹣2)﹣(x﹣5)=3,
∴(x﹣2)2+(x﹣5)2=a2+b2=(a﹣b)2+2ab=32+2×10=29;
(2)①∵AE=1,CF=3,正方形ABCD边长为x,
∴DE=x﹣1,DF=x﹣3.
故答案为:x﹣1,x﹣3;
②∵长方形EMFD的面积是15,
∴(x﹣1)(x﹣3)=15,
设x﹣1=a,x﹣3=b,则ab=15,a﹣b=2,
∴(x﹣1+x﹣3) =(a+b) =(a﹣b) +4ab=2 +4×15=64,
∵a≥0,b≥0,
∴x﹣1+x﹣3=a+b=8,
∴阴影部分面积为(x﹣1)2﹣(x﹣3)2=a ﹣b =(a+b)(a﹣b)=16.
解答题优生辅导训练(附答案)
1.计算:(2x﹣2)(x+1)﹣(x﹣1)2﹣(x+1)2
2.已知x+y=3,xy=2,求下列各式的值.
(1)x2+y2;
(2)(x﹣1)(y﹣1).
3.利用乘法公式解决下列问题:
(1)若x﹣y=8,xy=40.则x2+y2= ;
(2)已知,若x满足(25﹣x)(x﹣10)=﹣15,求(25﹣x)2+(x﹣10)2值.
4.已知多项式A=(x+2)2+(x+2)(1﹣x)﹣3.
(1)化简多项式A;
(2)若(x+1)2=5,求A的值.
5.阅读下列文字,寻找规律,解答下列各小题.
已知x≠1,计算:
(1﹣x)(1+x)=1﹣x2
(1﹣x)(1+x+x2)=1﹣x3
(1﹣x)(1+x+x2+x3)=1﹣x4
(1﹣x)(1+x+x2+x3+x4)=1﹣x5
(1)观察上式计算:(1﹣x)(1+x+x2+…+xm)= .
(2)计算:
①(1﹣2)(1+2+22+23+…+22022);
②2+22+23+24+…+2m.
6.阅读、理解、应用.
例:计算:20223﹣2021×2022×2023.
解:设2022=x,则原式=x3﹣(x﹣1) x (x+1)=x3﹣x(x2﹣1)=x=2022.
请你利用上述方法解答下列问题:
(1)计算:1232﹣124×122;
(2)若M=123456789×123456786,N=123456788×123456787,请比较M,N的大小;
(3)计算:
7.观察下列各式:
(a+1)(a2﹣a+1)=a3+1;
(a﹣2)(a2+2a+4)=a3﹣8;
(3a﹣2)(9a2+6a+4)=27a3﹣8.
(1)请你按照以上各式的运算规律,填空.
①(x﹣3)(x2+3x+9)= ;
②(2x+1)( )=8x3+1;
③( )(x2+xy+y2)=x3﹣y3.
(2)应用规律计算:(a2﹣b2)(a2+ab+b2)(a2﹣ab+b2).
8.如图1,边长为a的大正方形中有一个边长为b的小正方形,把图1中的阴影部分拼成一个长方形(如图2所示).
(1)写出根据上述操作利用阴影部分的面积关系得到的等式: .
(2)请应用(1)中的等式,解答下列问题:
①已知4a2﹣b2=24,2a+b=6,则2a﹣b= ;
②计算:2002﹣1992+1982﹣1972+…+42﹣32+22﹣12.
9.如图1,边长为a的大正方形有一个边长为b的小正方形,把图1中的阴影部分拼成一个长方形(如图2所示).
(1)上述操作能验证的等式是 ;(请选择正确的选项)
A.a2﹣b2=(a+b)(a﹣b)
B.a2﹣2ab+b2=(a﹣b)2
C.a2+ab=a(a+b)
(2)请利用你从(1)选出的等式,完成下列各题:
①已知4a2﹣b2=24,2a+b=6,则2a﹣b= .
②计算:(1﹣)(1﹣)(1﹣)…(1﹣)(1﹣).
10.乘法公式的探究及应用.
(1)如图1,是将图2阴影部分裁剪下来,重新拼成的一个长方形,面积是 ;如图2,阴影部分的面积是 ;比较图1,图2阴影部分的面积,可以得到乘法公式 ;
(2)运用你所得到的公式,计算下列各题:
①103×97;
②(2x+y﹣3)(2x﹣y+3).
11.若x满足(9﹣x)(x﹣4)=4,求(4﹣x)2+(x﹣9)2的值.
解:设9﹣x=a,x﹣4=b,
则(9﹣x)(x﹣4)=ab=4,a+b=(9﹣x)+(x﹣4)=5,
∴(4﹣x)2+(x﹣9)2=a2+b2=(a+b)2﹣2ab=52﹣2×4=17.
请仿照上面的方法求解下面的问题:
若x满足(x﹣2018)2+(x﹣2021)2=31,求(x﹣2018)(x﹣2021)的值.
12.用纸片拼图时,我们发现利用图1中的三种纸片(边长分别为a,b的正方形和长为b宽为a的长方形)各若干,可以拼出一些长方形来解释某些等式,比如图2可以解释为:(a+2b)(a+b)=a2+3ab+2b2.
(1)图3可以解释为等式;
(2)要拼出一个两边长为a+b,2a+b的长方形,需要图1中的三种纸片各多少块?请先画出图形,再利用整式乘法验证你的结论.
13.图1是一个长为2a、宽为2b的长方形,沿图中虚线用剪刀均分成四块小长方形,然后按图2的形状拼成一个正方形.
(1)观察图2,请你写出下列三个代数式(a+b)2,(a﹣b)2,ab之间的等量关系为 .
(2)运用你所得到的公式,计算:若m、n为实数,且mn=﹣3,m﹣n=4,试求m+n的值.
(3)如图3,点C是线段AB上的一点,以AC、BC为边向两边作正方形,设AB=8,两正方形的面积和S1+S2=26,求图中阴影部分面积.
14.阅读理解:
若x满足(80﹣x)(x﹣60)=30,求(80﹣x)2+(x﹣60)2的值.
解:设80﹣x=a,x﹣60=b,则(80﹣x)(x﹣60)=ab=30,a+b=(80﹣x)+(x﹣60)=20,
∴(80﹣x)2+(x﹣60)2=a2+b2=(a+b)2﹣2ab=202﹣2×30=340.
解决问题
(1)若x满足(20﹣x)(x﹣10)=﹣10,求(20﹣x)2+(x﹣10)2的值;
(2)若x满足(2022﹣x)2+(2020﹣x)2=4048,求(2022﹣x)(2020﹣x)的值.
15.数学活动课上,老师准备了图1中三种不同大小的正方形与长方形,拼成了一个如图2所示的正方形.
(1)请用两种不同的方法表示图2中阴影部分的面积和.
方法1: ;
方法2: .
(2)请你直接写出三个代数式:(a+b)2,a2+b2,ab之间的等量关系.
(3)根据(2)题中的等量关系,解决如下问题:
①已知m+n=5,m2+n2=20,求mn和(m﹣n)2的值;
②已知(x﹣2021)2+(x﹣2023)2=34,求(x﹣2022)2的值.
16.数学活动课上,张老师准备了若干个如图①的三种纸片,A种纸片是边长为a的正方形,B种纸片是边长为b的正方形,C种纸片是长为b,宽为a的长方形,并用A种纸片一张,B种纸片一张,C种纸片两张拼成如图②的大正方形.
(1)观察图②,写出代数式(a+b)2,a2+b2,ab之间的等量关系是 ;
(2)根据(1)中的等量关系,解决下列问题;
①已知a+b=4,a2+b2=10,求ab的值;
②已知(x﹣2021)2+(x﹣2019)2=130,直接写出x﹣2020的值.
17.如图1是一个长为4a,宽为b的长方形,沿图中虚线用剪刀平均分成四块小长方形,然后用四块小长方形拼成如图2的正方形.
(1)由图2可以直接写出(a+b)2,(a﹣b)2,ab之间的一个等量关系是 .
(2)根据(1)中的结论,解决下列问题:3x+4y=10,xy=2,求3x﹣4y的值;
(3)两个正方形ABCD,AEFG如图3摆放,边长分别为x,y.若x2+y2=34,BE=2,求图中阴影部分面积和.
18.问题背景:
在学习了完全平方公式后,老师布置了一道作业题:如图,长方形ABCD的长为a,宽为b,面积为4,周长为10,分别以a,b为边作正方形ABEF及ADGH,求两个正方形面积之和.小燕同学认真思考后,发现利用现有知识不能求出a,b的值,但可以用完全平方公式通过适当的变形求a2+b2的值,从而求得两个正方形面积之和.
(1)问题解决:请你依据上述内容填写已知条件和结果:
a+b= ,ab= ,a2+b2= .
(2)已知x+y=7,xy=10,求(x﹣y)2的值.
19.阅读理解:
若x满足(30﹣x)(x﹣10)=160,求(30﹣x)2+(x﹣10)2的值.
解:设30﹣x=a,x﹣10=b,则(30﹣x)(x﹣10)=ab=160,a+b=(30﹣x)+(x﹣10)=20,(30﹣x)2+(x﹣10)2=a2+b2=(a+b)2﹣2ab=202﹣2×160=80
解决问题:
(1)若x满足(2020﹣x)(x﹣2016)=2.则(2020﹣x)2+(x﹣2016)2= ;
(2)若x满足(2021﹣x)2+(x﹣2018)2=2020,求(2021﹣x)(x﹣2018)的值;
(3)如图,在长方形ABCD中,AB=20,BC=12,点E.F是BC、CD上的点,且BE=DF=x,分别以FC、CE为边在长方形ABCD外侧作正方形CFGH和CEMN,若长方形CEPF的面积为160平方单位,则图中阴影部分的面积和为 平方单位.
20.若x满足(x﹣4)(x﹣9)=6,求(x﹣4)2+(x﹣9)2的值.阅读下面求解的方法:
解:设(x﹣4)=a,(x﹣9)=b,则ab=(x﹣4)(x﹣9)=6,a﹣b=(x﹣4)﹣(x﹣9)=5
∴(x﹣4)2+(x﹣9)2=a2+b2=(a﹣b)2+2ab=52+2×6=37.
请仿照上面的方法求解下面的问题:
(1)若x满足(x﹣2)(x﹣5)=10,求(x﹣2)2+(x﹣5)2的值;
(2)如图,正方形ABCD中,E、F分别是AD、DC上的点,且AE=1,CF=3,长方形EMFD的面积是15,分别以MF、DF为边作正方形,若AD=x,则
①DE= ,DF= (用含x的代数式表示);
②直接写出图中阴影部分的面积.
参考答案
1.解:原式=2x2+2x﹣2x﹣2﹣(x2﹣2x+1)﹣(x2+2x+1)
=2x2+2x﹣2x﹣2﹣x2+2x﹣1﹣x2﹣2x﹣1
=﹣4.
2.解:(1)将x+y=3两边平方得:
(x+y)2=x2+2xy+y2=9,
将xy=2代入得:
x2+y2=5;
(2)原式=xy﹣(x+y)+1
=2﹣3+1
=0.
3.解:(1)∵x2+y2=(x﹣y)2+2xy,
把x﹣y=8,xy=40,代入上式,得x2+y2=82+2×40=144.
故答案是:144;
(2)设25﹣x=a,x﹣10=b,
由(a+b)2=a2+2ab+b2进行变形得,
a2+b2=(a+b)2﹣2ab,
∴(25﹣x)2+(x﹣10)2
=[(25﹣x)+(x﹣10)]2﹣2(25﹣x)(x﹣10)
=152﹣2×(﹣15)
=225+30
=255.
4.解:(1)A=x2+4x+4+x+2﹣x2﹣2x﹣3=3x+3;
(2)∵(x+1)2=5,
∴x+1=±,
则A=3x+3=3(x+1)=±3 .
5.解:(1)观察上面的式子得到原式=1﹣xm+1,
故答案为:1﹣xm+1;
(2)①当x=2时,原式=1﹣22023;
②当x=2时,(1﹣2)(1+2+22+23+…+2m)=1﹣2m+1,
∴1+2+22+23+…+2m=2m+1﹣1,
∴原式=2m+1﹣2.
6.解:(1)设123=x,
∴1232﹣124×122
=x2﹣(x+1)(x﹣1)
=x2﹣x2+1
=1;
(2)设123456786=x,
∴M=123456789×123456786
=(x+3) x
=x2+3x,
N=123456788×123456787
=(x+2)(x+1)
=x2+3x+2,
∴M<N;
(3)设++...+=x,
=(x+)(1+x)﹣(1+x+) x
=x+x2++x﹣x﹣x2﹣x
=.
7.解:(1)①(x﹣3)(x2+3x+9)=x3﹣27;
②(2x+1)(4x2﹣2x+1)=8x3+1;
③(x﹣y)(x2+xy+y2)=x3﹣y3.
故答案为:①x3﹣27;②4x2﹣2x+1;③x﹣y;
(2)(a2﹣b2)(a2+ab+b2)(a2﹣ab+b2)
=[(a+b)(a2﹣ab+b2)][(a﹣b)(a2+ab+b2)]
=(a3+b3)(a3﹣b3)
=a6﹣b6.
8.解:(1)根据上述操作利用阴影部分的面积关系得到的等式:a2﹣b2=(a+b)(a﹣b),
故答案为:a2﹣b2=(a+b)(a﹣b);
(2)①∵4a2﹣b2=24,
∴(2a+b)(2a﹣b)=24,
∵2a+b=6,
∴2a﹣b=4,
故答案为:4,
②2002﹣1992+1982﹣1972+…+42﹣32+22﹣12
=(200+199)(200﹣199)+(198+197)(198﹣197)+...+(4+3)(4﹣3)+(2+1)(2﹣1)
=200+199+198+197+...+4+3+2+1
=×(200+1)×200
=20100.
9.解:(1)图1中阴影部分的面积=a2﹣b2,图②中阴影部分的面积=(a+b)(a﹣b).
∴a2﹣b2=(a+b)(a﹣b).
故选A.
(2)①∵(2a+b)(2a﹣b)=4a2﹣b2.
∴6(2a﹣b)=24,
∴2a﹣b=24÷6=4.
故答案为:4.
②=
=
=
=.
10.解:(1)由拼图可知,图形1的长为(a+b),宽为(a﹣b),因此面积为(a+b)(a﹣b),图形2的阴影部分的面积为两个正方形的面积差,即a2﹣b2,
由图形1,图形2的面积相等可得,(a+b)(a﹣b)=a2﹣b2,
故答案为:(a+b)(a﹣b),a2﹣b2,(a+b)(a﹣b)=a2﹣b2;
(2)①103×97=(100+3)(100﹣3)
=1002﹣32
=10000﹣9
=9991;
②原式=(2x+y﹣3)[2x﹣(y﹣3)]
=(2x)2﹣(y﹣3)2
=4x2﹣(y2﹣6y+9)
=4x2﹣y2+6y﹣9.
11.解:设x﹣2018=a,x﹣2021=b,
则a2+b2=31,a﹣b=x﹣2018﹣x+2021=3,
∴a2﹣2ab+b2=(a﹣b)2=9,
∴31﹣2ab=9,
解得ab=11,
即(x﹣2018)(x﹣2021)=11.
12.解:(1)∵图3面积为(a+2b)(2a+b)=2a2+5ab+2b2,
∴图3可以解释为等式(a+2b)(2a+b)=2a2+5ab+2b2.
(2)需要边长为a的正方形2块,长为b宽为a的长方形3块,边长为b的正方形1块.如下图所示:
整式乘法验证,(a+b)(2a+b)=2a2+ab+2ab+b2=2a2+3ab+b2,
∴需要a×a的正方形2块,需要a×b的长方形3块,需要b×b的正方形1块.
13.解:(1)图2,大正方形的边长为a+b,因此面积为(a+b)2,
小正方形的边长为a﹣b,因此面积为(a﹣b)2,
每个长方形的长为a,宽为b,因此面积为ab,
由面积之间的关系可得,(a+b)2=(a﹣b)2+4ab,
故答案为:(a+b)2=(a﹣b)2+4ab;
(2)由(1)得,(m+n)2=(m﹣n)2+4mn,
即(m+n)2=42+4×(﹣3),
∴m+n=2或m+n=﹣2;
(3)设正方形ACDE的边长为a,正方形BCFG的边长为b,则S1=a2,S2=b2,
由于AB=8,两正方形的面积和S1+S2=26,
因此a+b=8,a2+b2=26,
∵(a+b)2=a2+2ab+b2,即64=26+2ab,
∴ab=19,
∴阴影部分的面积为ab=.
14.解:(1)设(20﹣x)=a,(x﹣10)=b,
则(20﹣x)(x﹣10)=ab=﹣10,a+b=(20﹣x)+(x﹣10)=10,
所以(20﹣x)2+(x﹣10)2=a2+b2=(a+b)2﹣2ab=102+2×10=120;
(2)设(2022﹣x)=a,(2020﹣x)=b,
则a﹣b=(2022﹣x)﹣(2020﹣x)=2,
因为(2022﹣x)2+(2020﹣x)2=4048,
所以(2022﹣x)2+(2020﹣x)2=a2+b2=(a﹣b)2+2ab=4048,
即22+2×(2022﹣x)(2020﹣x)=4048,
(2019﹣x)(2017﹣x)=2022.
15.解:(1)阴影两部分求和为a2+b2,用总面积减去空白部分面积为(a+b)2﹣2ab,
故答案为:a2+b2,(a+b)2﹣2ab;
(2)由题意得,a2+b2=(a+b)2﹣2ab;
(3)①由(2)题结论a2+b2=(a+b)2﹣2ab可得ab=,
∴m+n=5,m2+n2=20时,
mn=
=
=,
(m﹣n)2
=m2﹣2mn+n2;
=20﹣2×
=20﹣5
=15;
②设a=x﹣2021,b=x﹣2023,
可得a+b=(x﹣2021)+(x﹣2023)
=x﹣2021+x﹣2023
=2x﹣4044
=2(x﹣2022),
由(2)题结论a2+b2=(a+b)2﹣2ab可得,
(a+b)2=a2+2ab+b2,
又∵(a﹣b)2=[(x﹣2021)﹣(x﹣2023)]2=22=4,
且由(a﹣b)2=a2﹣2ab+b2,可得2ab=(a2+b2)﹣(a﹣b)2=(x﹣2021)2+(x﹣2023)2﹣[(x﹣2021)﹣(x﹣2023)]2=34﹣4=30,
∴(x﹣2022)2=()2====16.
16.解:(1)∵图形②是边长为(a+b)的正方形,
∴S=(a+b)2.
∵大正方形的面积由一个边长为a的正方形和一个边长为b的正方形以及两个长为b,宽为a的长方形组合而成,
∴S=a2+2ab+b2.
∴(a+b)2=a2+2ab+b2.
故答案为:(a+b)2=a2+2ab+b2.
(2)①∵a+b=4,
∴(a+b)2=16.
∴a2+2ab+b2=16.
∵a2+b2=10,
∴ab=3.
②设x﹣2020=a,则x﹣2021=a﹣1,x﹣2019=a+1.
∵(x﹣2021)2+(x﹣2019)2=130,
∴(a﹣1)2+(a+1)2=130.
∴a2﹣2a+1+a2+2a+1=130.
∴2a2=128.
∴a2=64.
即(x﹣2020)2=64.
∴x﹣2020=±8.
17.解:(1)∵大正方形的面积等于4个小长方形和小正方形面积之和,
∴(a+b)2=4ab+(b﹣a)2.
∴(a+b)2=(a﹣b)2+4ab.
故答案为:(a+b)2=(a﹣b)2+4ab.
(2)由(1)得:
(3x+4y)2=(3x﹣4y)2+4×3x×4y.
∴(3x﹣4y)2=(3x+4y)2﹣48xy
∴(3x﹣4y)2=100﹣96=4.
∴3x﹣4y=±2.
(3)∵ABCD,AEFG为正方形,边长分别为x,y.BE=2,
∴DG=BE=2,x﹣y=2.
∴(x﹣y)2=4.
∴x2﹣2xy+y2=4.
∵x2+y2=34,
∴2xy=30.
∴x2+2xy+y2=34+30,
∴(x+y)2=64.
∵x>0,y>0,
∴x+y=8.
∴=y+x=8.
18.解:(1)∵长方形ABCD的周长为10,
∴a+b=5.
∵长方形ABCD的面积为4,
∴ab=4.
∵(a+b)2=a2+2ab+b2,
∴a2+b2=(a+b)2﹣2ab=25﹣8=17.
故答案为:5,4,17.
(2)∵(x+y)2=x2+2xy+y2,(x﹣y)2=x2﹣2xy+y2,
∴(x﹣y)2=(x+y)2﹣4xy.
∴(x﹣y)2=72﹣4×10=9.
19.解:(1)设2020﹣x=a,x﹣2016=b,则(2020﹣x)(x﹣2016)=ab=2,a+b=(2020﹣x)+(x﹣2016)=4,
所以(2020﹣x)2+(x﹣2016)2=a2+b2=(a+b)2﹣2ab=42﹣2×2=12;
故答案为:12;
(2)设2021﹣x=a,x﹣2018=b,则(2021﹣x)2+(x﹣2018)2=a2+b2=2020,a+b=(2021﹣x)+(x﹣2018)=3,
所以(2021﹣x)(x﹣2018)=ab=[(a+b)2﹣(a2+b2)]=×(32﹣2020)=﹣;
答:(2021﹣x)(x﹣2018)的值为﹣;
(3)由题意得,FC=(20﹣x),EC=(12﹣x),
∵长方形CEPF的面积为160,
∴(20﹣x)(12﹣x)=160,
∴(20﹣x)(x﹣12)=﹣160,
∴阴影部分的面积为(20﹣x)2+(12﹣x)2,
设20﹣x=a,x﹣12=b,则(20﹣x)(x﹣12)=ab=﹣160,a+b=(20﹣x)+(x﹣12)=8,
所以(20﹣x)2+(x﹣12)2=(20﹣x)2+(12﹣x)2=a2+b2=(a+b)2﹣2ab=82﹣2×(﹣160)=384;
故答案为:384.
20.解:(1)设(x﹣2)=a,(x﹣5)=b,则ab=(x﹣2)(x﹣5)=10,a﹣b=(x﹣2)﹣(x﹣5)=3,
∴(x﹣2)2+(x﹣5)2=a2+b2=(a﹣b)2+2ab=32+2×10=29;
(2)①∵AE=1,CF=3,正方形ABCD边长为x,
∴DE=x﹣1,DF=x﹣3.
故答案为:x﹣1,x﹣3;
②∵长方形EMFD的面积是15,
∴(x﹣1)(x﹣3)=15,
设x﹣1=a,x﹣3=b,则ab=15,a﹣b=2,
∴(x﹣1+x﹣3) =(a+b) =(a﹣b) +4ab=2 +4×15=64,
∵a≥0,b≥0,
∴x﹣1+x﹣3=a+b=8,
∴阴影部分面积为(x﹣1)2﹣(x﹣3)2=a ﹣b =(a+b)(a﹣b)=16.
