2022-2023学年北师大版 九年级数学上册4.6利用相似三角形测高同步训练(word、含解析)
文档属性
| 名称 | 2022-2023学年北师大版 九年级数学上册4.6利用相似三角形测高同步训练(word、含解析) |
|
|
| 格式 | docx | ||
| 文件大小 | 362.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-20 00:00:00 | ||
图片预览

文档简介
4.6利用相似三角形测高 九年级数学同步训练(基础演练+巩固提升)
【北师大版】
基础演练:
一、单选题
1.在某次活动课中,甲、乙两个学习小组于同一时刻在阳光下对校园中一些物体进行了测量.下面是他们通过测量得到的一些信息:如图1,甲组测得一根直立于平地,长为80cm的竹竿的影长为60cm.如图2,乙组测得学校旗杆的影长为900cm.则旗杆的长为( ).
A.900cm B.1000cm C.1100cm D.1200cm
2.在设计人体雕像时,使雕像上部(腰部以上)与下部(腰部以下)的高度比,等于下部与全部的高度比,可以增加视觉美感.如图,按此比例设计一座高度为2m 的雷锋雕像,那么该雕像的下部设计高度约是( )(结果精确到 .参考数据: , , )
A. B. C. D.
3.如图,小勇在探究课本“综合与实践”中的“制作视力表”时,根据测试距离为5 m的标准视力表制作了一个测试距离为3 m的视力表.如果标准视力表中“E”的高a是72.7 mm,那么制作出的视力表中相应“E”的高b是( )
A.121.17 mm B.43.62 mm C.43.36 mm D.29.08 mm
4.如图是小明设计用手电来测量某古城墙高度的示意图.点P处放一水平的平面镜,光线从点A出发经平面镜反射后刚好射到古城墙CD的顶端C处,已知AB⊥BD,CD⊥BD,且测得AB=1.2米,BP=1.8米,PD=12米,那么该古城墙的高度是( )
A.6米 B.8米 C.18米 D.24米
5.如图,A,D是电线杆AB上的两个瓷壶,AC和DE分别表示太阳光线,若某一时刻线段AD在地面上的影长CE=1m,BD在地面上的影长BE=3m,瓷壶D到地面的距离DB=20m,则电线杆AB的高为( )
A.15m B. m C.21m D. m
二、填空题
6.如图,在一场羽毛球比赛中,站在场内M处的运动员林丹把球从N点击到了对方内的B点,已知网高OA=1.52米,OB=4米,OM=5米,则林丹起跳后击球点N离地面的距离NM= 米.
7.为了测量校园水平地面上一棵不可攀的树的高度,学校数学兴趣小组做了如下的探索:根据光的反射定律,利用一面镜子和一根皮尺,设计如图所示的测量方案:把一面很小的镜子放在离树底(B)8.4米的点E处,然后沿着直线BE后退到点D,这时恰好在镜子里看到树梢顶点A,再用皮尺量得DE=2.4米,观察者目高CD=1.6米,则树(AB)的高度为 米.
8.在阳光体育课上,小腾在打网球,如图所示,网高0.9m,球刚好打过网,而且落在离网6m的位置上,则球拍击球的高度h= m.
9.“今有井径五尺,不知其深,立五尺木于井上,从木末望水岸,入径四寸,问井深几何?”这是我国古代数学《九章算术》中的“井深几何”问题,它的题意可以由图获得,则井深为 尺.
10.小明在离路灯底部6处测得自己的影子长为1.2,小明的身高为1.6,那么路灯的高度为 .
三、解答题
11.《九章算术》中记载了一种测量井深的方法.如图所示,在井口B处立一根垂直于井口的木杆BD,从木杆的顶端D点观察井内水岸C点,视线DC与井口的直径AB交于点E.如果测得AB=1.8米,BD=1米,BE=0.2米.请求出井深AC的长.
12.如图,小明同学为了测量教学楼的高度 ,先在操场上点A处放一面镜子,从点A处后退 到点B处,恰好在镜子中看到楼的顶部E点;再将镜子向后移动 放在C处,从点C处向后退 点D处,恰好再次在镜子中看到楼的顶部E点,测得小明的眼睛距地面的高度 , 为 ,点O,A,B,C,D在同一水平线上,镜子可看成一个点.求教学楼的高度 .
13.如图,已知A、B两村庄的坐标分别为(2,2)、(7,4),一辆汽车在x轴上行驶,从原点O出发.
(1)汽车行驶到什么位置时离A村最近?写出此点的坐标;
(2)汽车行驶到什么位置时离B村最近?写出此点的坐标;
(3)请在图中画出汽车行驶到什么位置时,距离两村的和最短?
巩固提升:
一、单选题
1.在同一时刻,身高1.6米的小强在阳光下的影长为0.8米,一棵大树的影长为4.8米,则树的高度为( )
A.10米 B.9.6米 C.6.4米 D.4.8米
2.如图,为了测量一池塘的宽DE,在岸边找到一点C,测得CD=30m,在DC的延长线上找一点A,测得AC=5m,过点A作AB∥DE交EC的延长线于B,测出AB=8m,则池塘的宽DE为( )
A.32m B.36m C.48m D.56m
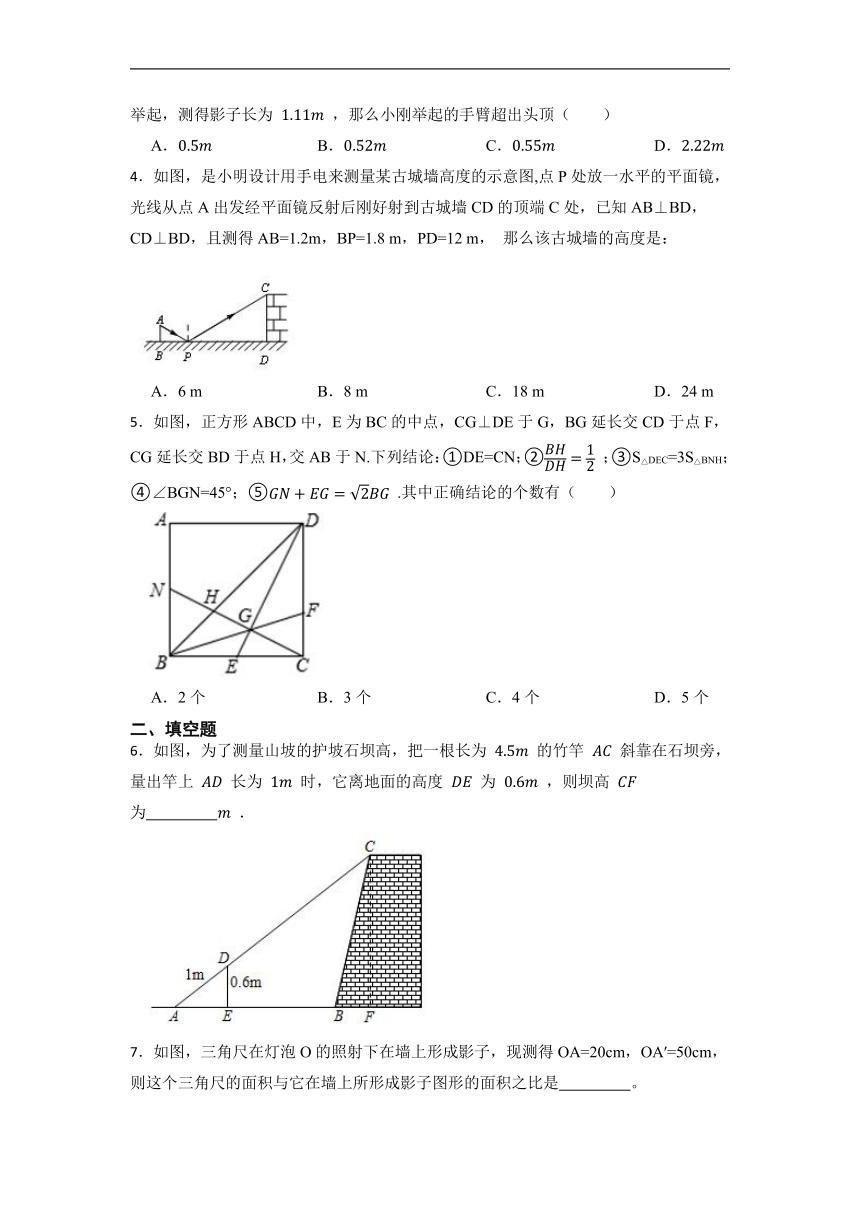
3.小刚身高 ,测得他站立在阳光下的影子长为 ,紧接着他把手臂竖直举起,测得影子长为 ,那么小刚举起的手臂超出头顶( )
A. B. C. D.
4.如图,是小明设计用手电来测量某古城墙高度的示意图,点P处放一水平的平面镜,光线从点A出发经平面镜反射后刚好射到古城墙CD的顶端C处,已知AB⊥BD,CD⊥BD,且测得AB=1.2m,BP=1.8 m,PD=12 m, 那么该古城墙的高度是:
A.6 m B.8 m C.18 m D.24 m
5.如图,正方形ABCD中,E为BC的中点,CG⊥DE于G,BG延长交CD于点F,CG延长交BD于点H,交AB于N.下列结论:①DE=CN;② ;③S△DEC=3S△BNH;④∠BGN=45°;⑤ .其中正确结论的个数有( )
A.2个 B.3个 C.4个 D.5个
二、填空题
6.如图,为了测量山坡的护坡石坝高,把一根长为 的竹竿 斜靠在石坝旁,量出竿上 长为 时,它离地面的高度 为 ,则坝高 为 .
7.如图,三角尺在灯泡O的照射下在墙上形成影子,现测得OA=20cm,OA′=50cm,则这个三角尺的面积与它在墙上所形成影子图形的面积之比是 。
8.如图,现有一张矩形纸片ABCD,其中AB=4cm,BC=6cm,点E是BC的中点.将纸片沿直线AE折叠,使点B落在梯形AECD内,记为点B′,那么B′、C两点之间的距离是 cm.
9.在某时刻的阳光照耀下,高为4米的旗杆在水平地面上的影长为5米,附近一个建筑物的影长为20米,则该建筑物的高为 米.
10.墙壁CD上D处有一盏灯(如图),小明站在A站测得他的影长与身长相等都为1.5m,他向墙壁走1m到B处时发现影子刚好落在A点,则灯泡与地面的距离CD= m.
三、解答题
11.如图,M、N为山两侧的两个村庄,为了两村交通方便,根据国家的惠民政策,政府决定打一直线涵洞.工程人员为了计算工程量,必须计算M、N两点之间的直线距离,选择测量点A、B、C,点B、C分别在AM、AN上,现测得AM=1千米、AN=1.8千米,AB=54米、BC=45米、AC=30米,求M、N两点之间的直线距离.
12.如图,AB表示路灯,当身高为1.6米的小名站在离路灯1.6的D处时,他测得自己在路灯下的影长DE与身高CD相等,当小明继续沿直线BD往前走到E点时,画出此时小明的影子,并计算此时小明的影长.
13.“今有邑,东西七里,南北九里,各开中门,出东门一十五里有木,问:出南门几何步而见木?”这段话摘自《九章算术》,意思是说:如图,矩形城池ABCD,东边城墙AB长9里,南边城墙AD长7里,东门点E,南门点F分别是AB、AD的中点,EG⊥AB,FH⊥AD,EG=15里,HG经过点A,问FH多少里?
答案解析
基础演练:
1.【答案】D
【解析】【解答】∵同一时刻物高与影长成正比,
∴ = ,
解得旗杆的高度=1200cm;
故选D.
【分析】根据同一时刻物高与影长成正比即可求出旗杆的高度;
2.【答案】B
【解析】【解答】解:设该雕像的下部设计高度约是xm,则上部的高度为(2-x)m,
∵使雕像上部(腰部以上)与下部(腰部以下)的高度比,等于下部与全部的高度比,
∴
解之:(舍去)
经检验,x1是方程的根,
故答案为:B.
【解答】设该雕像的下部设计高度约是xm,则上部的高度为(2-x)m,根据雕像上部(腰部以上)与下部(腰部以下)的高度比,等于下部与全部的高度比,建立关于x的方程,解方程求出符合题意的x的值.
3.【答案】B
【解析】【解答】解:如下图所示:
由题意可知: ,
故有: ,即 ,解得 ,
故答案为:B.
【分析】图形中隐含BC∥ED,可得到△ABC∽△ADE,利用相似三角形的对应边成比例,可得比例式,由此可求出b的值.
4.【答案】B
【解析】解答:由题意知:∠ABP=∠CDP= ,∠APB=∠CPD,
∴Rt△ABP∽Rt△CDP,
∴ ,
∴CD= =8(米).
故选:B.
分析:由已知条件得△ABP∽△CDP,根据相似形的性质得 ,代入数据进行解答.此题综合考查了平面镜反射和相似三角形在测量中的应用.
5.【答案】B
【解析】【解答】解:∵太阳光线是平行的,
∴AC∥DE,
∴△BDE∽△BAC,
∴ ,
∵BE=3m,CE=1m,
∴BC=4m,
∴ ,
解得:AB= .
故选:B.
【分析】根据阳光是平行的得到△BDE∽△BAC,利用相似三角形对应边成比例得到关于AB的比例式,再代入数据求解即可.
6.【答案】3.42
【解析】【解答】解:根据题意得:AO⊥BM,NM⊥BM,
∴AO∥NM,
∴△ABO∽△NBM,
∴ ,
∵OA=1.52米,OB=4米,OM=5米,
∴BM=OB+OM=4+5=9(米),
∴ ,
解得:NM=3.42(米),
∴林丹起跳后击球点N离地面的距离NM为3.42米.
故答案为:3.42.
【分析】根据同一平面内垂直于同一直线的两条直线互相平行得出AO∥NM,根据平行于三角形一边的直线截其它两边,所截的三角形与原三角形相似得出△ABO∽△NBM,根据相似三角形对应边成比例建立方程即可求出MN的长度。
7.【答案】5.6
【解析】【解答】解:根据题意,易得∠CDE=∠ABE=90°,∠CED=∠AEB,
则△ABE∽△CDE,
则 ,即 ,
解得:AB=5.6米.
故答案为:5.6
【分析】将实际问题转化为数学问题,可证得△ABE∽△CDE,的长对应边成比例,建立关于AB的方程,求解即可。
8.【答案】1.5
【解析】【解答】解:∵DE∥BC,
∴△ADE∽△ACB,
DE:BC=AE:AB,
则 ,
∴h=1.5m.
故答案为:1.5.
【分析】如下图,根据球网和击球时球拍的垂直线段平行即DE∥BC可知,△ADE∽△ACB,根据其相似比即可求解.
9.【答案】57.5
【解析】【解答】如图,AB与BC交于点F,
由题意得△ABF∽△ADE,
∴AB:AD=BF:DE,即5:AD=0.4:5,
解得:AD=62.5(尺),
则BD=AD-AB=62.5-5=57.5(尺)
故答案为57.5.
【分析】如图,设AB与BC交于点F,根据平行于三角形一边的直线和其它两边相交,所构成的三角形与原三角形相似可得△ABF∽△ADE,由相似三角形的对应边成比例可得AB:AD=BF:DE,从中求出AD,j进而可求BD的长,即井深 .
10.【答案】9.6
【解析】【解答】解:如图,AB=1.6m,DB=6m,BE=1.2m,
∵AB⊥DE,CD⊥DE,
∴AB//CD
∴△EAB∽△ECD,
∴,
∵AB=1.6m,DB=6m,BE=1.2m,
∴,
解得:CD=9.6m.
故答案为:9.6.
【分析】画出示意图,由题意可得AB=1.6m,DB=6m,BE=1.2m,易证△EAB∽△ECD,然后根据相似三角形的性质进行计算即可.
11.【答案】解:由题意,BD∥AC.
∴△BDE∽△ACE.
∴.
∴.
解得AC=8.
答:井深AC的长为8米.
【解析】【分析】先证明△BDE∽△ACE,再利用相似三角形的性质可得,然后将数据代入计算可得AC=8。
12.【答案】解:由已知得, , , ,
, ,
∴在 和 中
∴
∴ ,即 ,
∴ ,
在 和 中
∴
∴ ,即 ,
∴
∴ ,
∴
∴ ,
答:教学楼的高度 为 .
【解析】【分析】结合图形,利用相似三角形的判定与性质计算求解即可。
13.【答案】解:(1)在x轴上离A村最近的地方是过A作x轴垂线的垂足,即点(2,0);(2)离B村最近的是点(7,0);(3)A关于x轴的对称的点C(2,﹣2),并将其与B连接起来,容易看出△CDE∽△BDF,ED:DF=CE:BF=1:2,故所连直线与x轴交于点D(,0),所以当汽车行驶到D处时,距离两村的和最短.
【解析】【分析】(1)(2)根据垂线段最短的原则确定最近点的位置,表示出坐标.
(3)作出点A关于x轴的对称点C,连接CB,交于x轴于点D,则有AD=CD,根据三角形三边关系:任意两边之和大于第三边,知点C与点B的所有连线中,CB是最短的线段,所以点D是满足要求的点.
巩固提升:
1.【答案】B
【解析】【解答】解:设树高为x米,
因为 ,
所以 ,
解得:x=9.6.
答:这棵树的高度为9.6米.
故选:B.
【分析】在同一时刻物高和影长成正比,即在同一时刻的两个物体,影子,经过物体顶部的太阳光线三者构成的两个直角三角形相似.
2.【答案】C
【解析】【解答】∵AB∥DE,
∴△ABC∽△DEC,
∴ ,
∴ ,
∴DE=48m,
故答案为:C.
【分析】先根据AB∥DE证得△ABC∽△DEC,然后利用相似三角形对应边成比例得,即,故可求出DE.
3.【答案】B
【解析】【解答】解:设手臂竖直举起时总高度 ,列方程得:
,
解得 ,
,
所以小刚举起的手臂超出头顶的高度为 .
故答案为:B.
【分析】同一时刻,物体的实际高度与影长成比例,根据等量关系列方程。
4.【答案】B
【解析】【分析】因为小明和古城墙均和地面垂直,且光线的入射角等于反射角,因此构成一组相似三角形,利用对应边成比例即可解答.
【解答】由题意可得△PAB∽△PCD
∴
即
CD=8m,
答:古城墙的高度为8m.
选B
5.【答案】D
【解析】【解答】解:①∵在正方形ABCD中, , ,
∴
即:
∴ (ASA)
∴CN= DE,故①符合题意;
②∴在正方形ABCD中, ,
∴ ,
∴ ,
∵ ,E为BC的中点, 四边形ABCD是正方形
∴ ,
∴ ,故②符合题意;
③如下图示,过H点作 ,
∴根据 ,有 ,
则:
∴ ,
即是: ,故③符合题意 ;
④过B作BP⊥CN于P,BQ⊥DG,交DE的延长线于E,
∴∠BPC=∠BQD=∠PGQ=90°,
∴四边形PBQG是矩形,
∴∠PBQ=90°,
∵∠ABC=90°,
∴∠NBP=∠QBE,
由①得:△BNC≌△CED,
∴EC=BN,
∵E是BC的中点,
∴BE=EC,
∴BE=BN,
∵∠BPN=∠BQE=90°,
∴△BPN≌△BQE,
∴BP=BQ,
∴四边形PBQG是正方形,
∴∠BGE=45°,故④符合题意;
⑤如图示,连接N,E
设 ,则 , ,
∵CG⊥DE,
∴ ,
,
由 的面积可得:
化简得: ,
∴ ,
则有:
∴ ,
∵ ,
∴ ,
∴ ,
∴ ,
则 ,
,
并∵
∴
∴ ,故⑤符合题意.
综上所述,
故答案为:D.
【分析】根据题目已知证明 可判断①符合题意;证明 可判断②符合题意;过H点作 ,利用 , 求解即可判断③符合题意;添加辅助线过B作BP⊥CN于P,BQ⊥DG,交DE的延长线于E,利用△BNC≌△CED,证得△BPN≌△BQE,即可判断④符合题意;连接N,E,设 ,则 , ,利用勾股定理求出CN,CE的长,然后根据 的面积求出GE,GN,再证 ,利用相似三角形对应边成比例,求出BG,BF的长,即可得⑤符合题意.
6.【答案】2.7
【解析】【解答】解:如图,过 作 于 ,则 ,
∴ ,即 ,
解得 ,
故答案为:2.7
【分析】先求出,再求出,最后求解即可。
7.【答案】4:25
【解析】【解答】∵ ,∴三角尺的面积与它在墙上形成的影子的面积的比= .
【分析】根据物高 :影长可得相似比的值,再根据相似三角形的面积的比等于相似比的平方可求解。
8.【答案】
【解析】【解答】解:如图所示:过点B′作B′F⊥BC,垂足为F,连接B′C.
∵点E是BC的中点,
∴BE= .
在Rt△ABE中,AE= .
由射影定理可知;OE AE=BE2,
∴OE= .
由翻折的性质可知;BO⊥AE.
∴ .
∴OB= .
∴BB′= .
∵∠OBE=∠FBB′,∠BOE=∠BFB′,
∴△BOE∽△BFB′.
∴ ,即 = .
解得: .
∴FC= .
在Rt△B′FC中,B′C= = .
故答案为: .
【分析】先在Rt△ABE中,用勾股定理求得AE,再根据射影定理求得OE,运用△ABE面积的两种表示求得OB的长度,运用△BOE∽△BFB′求得BF,最后在Rt△B′FC中,运用勾股定理求得B′C。
9.【答案】16
【解析】【解答】解:∵,
∴,
∴建筑物的高=16(米)
故答案为:16.
【分析】在同一时刻物高和影长成正比,即在同一时刻的两个物体,影子,经过物体顶部的太阳光线三者构成的三角形相似,根据相似三角形的性质列出等式,即可求出答案.
10.【答案】
【解析】【解答】如图:
根据题意得:BG=AF=AE=1.5m,AB=1m,
∵BG∥AF∥CD
∴△EAF∽△ECD,△ABG∽△ACD,
∴AE:EC=AF:CD,AB:AC=BG:CD,
设BC=xm,CD=ym,则CE=(x+2.5)m,AC=(x+1)m,
则 , ,
解得:x=2,y=4.5,
即CD=4.5米,
故答案为:4.5.
【分析】首先抽象出数学图形,根据平行于三角形一边的直线截其他两边,所截得的三角形与原三角形系数得出△EAF∽△ECD,△ABG∽△ACD,根据相似三角形对应边成比例得出AE:EC=AF:CD,AB:AC=BG:CD,设BC=xm,CD=ym,则CE=(x+2.5)m,AC=(x+1)m,根据比例式建立出方程组,求解即可得出答案。
11.【答案】解:在△ABC与△AMN中,
= , = ,∴ ,又∵∠A=∠A,
∴△ABC∽△AMN,
∴ ,即 ,
解得:MN=1500米,
答:M、N两点之间的直线距离是1500米
【解析】【分析】先根据相似三角形的判定得出△ABC∽△AMN,再利用相似三角形的性质解答即可.
12.【答案】解:如图所示:线段EG表示小明此时的影子;根据题意得:BD=CD=DE=EF=1.6米,AB∥CD,∴BE=3.2米,△CDE∽△ABE,∴ ,即 ,解得:AB=3.2米,同理:△FEG∽△ABG,∴ ,即 ,解得:EG=3.2米;答:此时小明的影长为3.2米.
【解析】【分析】灯A与小明一次所在位置CD的顶端C的连线与地面BD的延长线的相交于点GEG即为所求影子。易得△CDE∽△ABE可求得AB=3.2米,再利用△FEG∽△ABG,可求得小明现在的影长为3.2米。
13.【答案】解:∵EG⊥AB,FH⊥AD,HG经过点A,
∴FA∥EG,EA∥FH,
∴∠AEG=∠HFA=90°,∠EAG=∠FHA,
∴△GEA∽△AFH,
∴ .
∵AB=9里,AD=7里,EG=15里,
∴AF=3.5里,AE=4.5里,
∴ ,
∴FH=1.05里.
【解析】【分析】首先根据题意得到△GEA∽△AFH,然后利用相似三角形的对应边的比相等列出比例式求得答案即可.
【北师大版】
基础演练:
一、单选题
1.在某次活动课中,甲、乙两个学习小组于同一时刻在阳光下对校园中一些物体进行了测量.下面是他们通过测量得到的一些信息:如图1,甲组测得一根直立于平地,长为80cm的竹竿的影长为60cm.如图2,乙组测得学校旗杆的影长为900cm.则旗杆的长为( ).
A.900cm B.1000cm C.1100cm D.1200cm
2.在设计人体雕像时,使雕像上部(腰部以上)与下部(腰部以下)的高度比,等于下部与全部的高度比,可以增加视觉美感.如图,按此比例设计一座高度为2m 的雷锋雕像,那么该雕像的下部设计高度约是( )(结果精确到 .参考数据: , , )
A. B. C. D.
3.如图,小勇在探究课本“综合与实践”中的“制作视力表”时,根据测试距离为5 m的标准视力表制作了一个测试距离为3 m的视力表.如果标准视力表中“E”的高a是72.7 mm,那么制作出的视力表中相应“E”的高b是( )
A.121.17 mm B.43.62 mm C.43.36 mm D.29.08 mm
4.如图是小明设计用手电来测量某古城墙高度的示意图.点P处放一水平的平面镜,光线从点A出发经平面镜反射后刚好射到古城墙CD的顶端C处,已知AB⊥BD,CD⊥BD,且测得AB=1.2米,BP=1.8米,PD=12米,那么该古城墙的高度是( )
A.6米 B.8米 C.18米 D.24米
5.如图,A,D是电线杆AB上的两个瓷壶,AC和DE分别表示太阳光线,若某一时刻线段AD在地面上的影长CE=1m,BD在地面上的影长BE=3m,瓷壶D到地面的距离DB=20m,则电线杆AB的高为( )
A.15m B. m C.21m D. m
二、填空题
6.如图,在一场羽毛球比赛中,站在场内M处的运动员林丹把球从N点击到了对方内的B点,已知网高OA=1.52米,OB=4米,OM=5米,则林丹起跳后击球点N离地面的距离NM= 米.
7.为了测量校园水平地面上一棵不可攀的树的高度,学校数学兴趣小组做了如下的探索:根据光的反射定律,利用一面镜子和一根皮尺,设计如图所示的测量方案:把一面很小的镜子放在离树底(B)8.4米的点E处,然后沿着直线BE后退到点D,这时恰好在镜子里看到树梢顶点A,再用皮尺量得DE=2.4米,观察者目高CD=1.6米,则树(AB)的高度为 米.
8.在阳光体育课上,小腾在打网球,如图所示,网高0.9m,球刚好打过网,而且落在离网6m的位置上,则球拍击球的高度h= m.
9.“今有井径五尺,不知其深,立五尺木于井上,从木末望水岸,入径四寸,问井深几何?”这是我国古代数学《九章算术》中的“井深几何”问题,它的题意可以由图获得,则井深为 尺.
10.小明在离路灯底部6处测得自己的影子长为1.2,小明的身高为1.6,那么路灯的高度为 .
三、解答题
11.《九章算术》中记载了一种测量井深的方法.如图所示,在井口B处立一根垂直于井口的木杆BD,从木杆的顶端D点观察井内水岸C点,视线DC与井口的直径AB交于点E.如果测得AB=1.8米,BD=1米,BE=0.2米.请求出井深AC的长.
12.如图,小明同学为了测量教学楼的高度 ,先在操场上点A处放一面镜子,从点A处后退 到点B处,恰好在镜子中看到楼的顶部E点;再将镜子向后移动 放在C处,从点C处向后退 点D处,恰好再次在镜子中看到楼的顶部E点,测得小明的眼睛距地面的高度 , 为 ,点O,A,B,C,D在同一水平线上,镜子可看成一个点.求教学楼的高度 .
13.如图,已知A、B两村庄的坐标分别为(2,2)、(7,4),一辆汽车在x轴上行驶,从原点O出发.
(1)汽车行驶到什么位置时离A村最近?写出此点的坐标;
(2)汽车行驶到什么位置时离B村最近?写出此点的坐标;
(3)请在图中画出汽车行驶到什么位置时,距离两村的和最短?
巩固提升:
一、单选题
1.在同一时刻,身高1.6米的小强在阳光下的影长为0.8米,一棵大树的影长为4.8米,则树的高度为( )
A.10米 B.9.6米 C.6.4米 D.4.8米
2.如图,为了测量一池塘的宽DE,在岸边找到一点C,测得CD=30m,在DC的延长线上找一点A,测得AC=5m,过点A作AB∥DE交EC的延长线于B,测出AB=8m,则池塘的宽DE为( )
A.32m B.36m C.48m D.56m
3.小刚身高 ,测得他站立在阳光下的影子长为 ,紧接着他把手臂竖直举起,测得影子长为 ,那么小刚举起的手臂超出头顶( )
A. B. C. D.
4.如图,是小明设计用手电来测量某古城墙高度的示意图,点P处放一水平的平面镜,光线从点A出发经平面镜反射后刚好射到古城墙CD的顶端C处,已知AB⊥BD,CD⊥BD,且测得AB=1.2m,BP=1.8 m,PD=12 m, 那么该古城墙的高度是:
A.6 m B.8 m C.18 m D.24 m
5.如图,正方形ABCD中,E为BC的中点,CG⊥DE于G,BG延长交CD于点F,CG延长交BD于点H,交AB于N.下列结论:①DE=CN;② ;③S△DEC=3S△BNH;④∠BGN=45°;⑤ .其中正确结论的个数有( )
A.2个 B.3个 C.4个 D.5个
二、填空题
6.如图,为了测量山坡的护坡石坝高,把一根长为 的竹竿 斜靠在石坝旁,量出竿上 长为 时,它离地面的高度 为 ,则坝高 为 .
7.如图,三角尺在灯泡O的照射下在墙上形成影子,现测得OA=20cm,OA′=50cm,则这个三角尺的面积与它在墙上所形成影子图形的面积之比是 。
8.如图,现有一张矩形纸片ABCD,其中AB=4cm,BC=6cm,点E是BC的中点.将纸片沿直线AE折叠,使点B落在梯形AECD内,记为点B′,那么B′、C两点之间的距离是 cm.
9.在某时刻的阳光照耀下,高为4米的旗杆在水平地面上的影长为5米,附近一个建筑物的影长为20米,则该建筑物的高为 米.
10.墙壁CD上D处有一盏灯(如图),小明站在A站测得他的影长与身长相等都为1.5m,他向墙壁走1m到B处时发现影子刚好落在A点,则灯泡与地面的距离CD= m.
三、解答题
11.如图,M、N为山两侧的两个村庄,为了两村交通方便,根据国家的惠民政策,政府决定打一直线涵洞.工程人员为了计算工程量,必须计算M、N两点之间的直线距离,选择测量点A、B、C,点B、C分别在AM、AN上,现测得AM=1千米、AN=1.8千米,AB=54米、BC=45米、AC=30米,求M、N两点之间的直线距离.
12.如图,AB表示路灯,当身高为1.6米的小名站在离路灯1.6的D处时,他测得自己在路灯下的影长DE与身高CD相等,当小明继续沿直线BD往前走到E点时,画出此时小明的影子,并计算此时小明的影长.
13.“今有邑,东西七里,南北九里,各开中门,出东门一十五里有木,问:出南门几何步而见木?”这段话摘自《九章算术》,意思是说:如图,矩形城池ABCD,东边城墙AB长9里,南边城墙AD长7里,东门点E,南门点F分别是AB、AD的中点,EG⊥AB,FH⊥AD,EG=15里,HG经过点A,问FH多少里?
答案解析
基础演练:
1.【答案】D
【解析】【解答】∵同一时刻物高与影长成正比,
∴ = ,
解得旗杆的高度=1200cm;
故选D.
【分析】根据同一时刻物高与影长成正比即可求出旗杆的高度;
2.【答案】B
【解析】【解答】解:设该雕像的下部设计高度约是xm,则上部的高度为(2-x)m,
∵使雕像上部(腰部以上)与下部(腰部以下)的高度比,等于下部与全部的高度比,
∴
解之:(舍去)
经检验,x1是方程的根,
故答案为:B.
【解答】设该雕像的下部设计高度约是xm,则上部的高度为(2-x)m,根据雕像上部(腰部以上)与下部(腰部以下)的高度比,等于下部与全部的高度比,建立关于x的方程,解方程求出符合题意的x的值.
3.【答案】B
【解析】【解答】解:如下图所示:
由题意可知: ,
故有: ,即 ,解得 ,
故答案为:B.
【分析】图形中隐含BC∥ED,可得到△ABC∽△ADE,利用相似三角形的对应边成比例,可得比例式,由此可求出b的值.
4.【答案】B
【解析】解答:由题意知:∠ABP=∠CDP= ,∠APB=∠CPD,
∴Rt△ABP∽Rt△CDP,
∴ ,
∴CD= =8(米).
故选:B.
分析:由已知条件得△ABP∽△CDP,根据相似形的性质得 ,代入数据进行解答.此题综合考查了平面镜反射和相似三角形在测量中的应用.
5.【答案】B
【解析】【解答】解:∵太阳光线是平行的,
∴AC∥DE,
∴△BDE∽△BAC,
∴ ,
∵BE=3m,CE=1m,
∴BC=4m,
∴ ,
解得:AB= .
故选:B.
【分析】根据阳光是平行的得到△BDE∽△BAC,利用相似三角形对应边成比例得到关于AB的比例式,再代入数据求解即可.
6.【答案】3.42
【解析】【解答】解:根据题意得:AO⊥BM,NM⊥BM,
∴AO∥NM,
∴△ABO∽△NBM,
∴ ,
∵OA=1.52米,OB=4米,OM=5米,
∴BM=OB+OM=4+5=9(米),
∴ ,
解得:NM=3.42(米),
∴林丹起跳后击球点N离地面的距离NM为3.42米.
故答案为:3.42.
【分析】根据同一平面内垂直于同一直线的两条直线互相平行得出AO∥NM,根据平行于三角形一边的直线截其它两边,所截的三角形与原三角形相似得出△ABO∽△NBM,根据相似三角形对应边成比例建立方程即可求出MN的长度。
7.【答案】5.6
【解析】【解答】解:根据题意,易得∠CDE=∠ABE=90°,∠CED=∠AEB,
则△ABE∽△CDE,
则 ,即 ,
解得:AB=5.6米.
故答案为:5.6
【分析】将实际问题转化为数学问题,可证得△ABE∽△CDE,的长对应边成比例,建立关于AB的方程,求解即可。
8.【答案】1.5
【解析】【解答】解:∵DE∥BC,
∴△ADE∽△ACB,
DE:BC=AE:AB,
则 ,
∴h=1.5m.
故答案为:1.5.
【分析】如下图,根据球网和击球时球拍的垂直线段平行即DE∥BC可知,△ADE∽△ACB,根据其相似比即可求解.
9.【答案】57.5
【解析】【解答】如图,AB与BC交于点F,
由题意得△ABF∽△ADE,
∴AB:AD=BF:DE,即5:AD=0.4:5,
解得:AD=62.5(尺),
则BD=AD-AB=62.5-5=57.5(尺)
故答案为57.5.
【分析】如图,设AB与BC交于点F,根据平行于三角形一边的直线和其它两边相交,所构成的三角形与原三角形相似可得△ABF∽△ADE,由相似三角形的对应边成比例可得AB:AD=BF:DE,从中求出AD,j进而可求BD的长,即井深 .
10.【答案】9.6
【解析】【解答】解:如图,AB=1.6m,DB=6m,BE=1.2m,
∵AB⊥DE,CD⊥DE,
∴AB//CD
∴△EAB∽△ECD,
∴,
∵AB=1.6m,DB=6m,BE=1.2m,
∴,
解得:CD=9.6m.
故答案为:9.6.
【分析】画出示意图,由题意可得AB=1.6m,DB=6m,BE=1.2m,易证△EAB∽△ECD,然后根据相似三角形的性质进行计算即可.
11.【答案】解:由题意,BD∥AC.
∴△BDE∽△ACE.
∴.
∴.
解得AC=8.
答:井深AC的长为8米.
【解析】【分析】先证明△BDE∽△ACE,再利用相似三角形的性质可得,然后将数据代入计算可得AC=8。
12.【答案】解:由已知得, , , ,
, ,
∴在 和 中
∴
∴ ,即 ,
∴ ,
在 和 中
∴
∴ ,即 ,
∴
∴ ,
∴
∴ ,
答:教学楼的高度 为 .
【解析】【分析】结合图形,利用相似三角形的判定与性质计算求解即可。
13.【答案】解:(1)在x轴上离A村最近的地方是过A作x轴垂线的垂足,即点(2,0);(2)离B村最近的是点(7,0);(3)A关于x轴的对称的点C(2,﹣2),并将其与B连接起来,容易看出△CDE∽△BDF,ED:DF=CE:BF=1:2,故所连直线与x轴交于点D(,0),所以当汽车行驶到D处时,距离两村的和最短.
【解析】【分析】(1)(2)根据垂线段最短的原则确定最近点的位置,表示出坐标.
(3)作出点A关于x轴的对称点C,连接CB,交于x轴于点D,则有AD=CD,根据三角形三边关系:任意两边之和大于第三边,知点C与点B的所有连线中,CB是最短的线段,所以点D是满足要求的点.
巩固提升:
1.【答案】B
【解析】【解答】解:设树高为x米,
因为 ,
所以 ,
解得:x=9.6.
答:这棵树的高度为9.6米.
故选:B.
【分析】在同一时刻物高和影长成正比,即在同一时刻的两个物体,影子,经过物体顶部的太阳光线三者构成的两个直角三角形相似.
2.【答案】C
【解析】【解答】∵AB∥DE,
∴△ABC∽△DEC,
∴ ,
∴ ,
∴DE=48m,
故答案为:C.
【分析】先根据AB∥DE证得△ABC∽△DEC,然后利用相似三角形对应边成比例得,即,故可求出DE.
3.【答案】B
【解析】【解答】解:设手臂竖直举起时总高度 ,列方程得:
,
解得 ,
,
所以小刚举起的手臂超出头顶的高度为 .
故答案为:B.
【分析】同一时刻,物体的实际高度与影长成比例,根据等量关系列方程。
4.【答案】B
【解析】【分析】因为小明和古城墙均和地面垂直,且光线的入射角等于反射角,因此构成一组相似三角形,利用对应边成比例即可解答.
【解答】由题意可得△PAB∽△PCD
∴
即
CD=8m,
答:古城墙的高度为8m.
选B
5.【答案】D
【解析】【解答】解:①∵在正方形ABCD中, , ,
∴
即:
∴ (ASA)
∴CN= DE,故①符合题意;
②∴在正方形ABCD中, ,
∴ ,
∴ ,
∵ ,E为BC的中点, 四边形ABCD是正方形
∴ ,
∴ ,故②符合题意;
③如下图示,过H点作 ,
∴根据 ,有 ,
则:
∴ ,
即是: ,故③符合题意 ;
④过B作BP⊥CN于P,BQ⊥DG,交DE的延长线于E,
∴∠BPC=∠BQD=∠PGQ=90°,
∴四边形PBQG是矩形,
∴∠PBQ=90°,
∵∠ABC=90°,
∴∠NBP=∠QBE,
由①得:△BNC≌△CED,
∴EC=BN,
∵E是BC的中点,
∴BE=EC,
∴BE=BN,
∵∠BPN=∠BQE=90°,
∴△BPN≌△BQE,
∴BP=BQ,
∴四边形PBQG是正方形,
∴∠BGE=45°,故④符合题意;
⑤如图示,连接N,E
设 ,则 , ,
∵CG⊥DE,
∴ ,
,
由 的面积可得:
化简得: ,
∴ ,
则有:
∴ ,
∵ ,
∴ ,
∴ ,
∴ ,
则 ,
,
并∵
∴
∴ ,故⑤符合题意.
综上所述,
故答案为:D.
【分析】根据题目已知证明 可判断①符合题意;证明 可判断②符合题意;过H点作 ,利用 , 求解即可判断③符合题意;添加辅助线过B作BP⊥CN于P,BQ⊥DG,交DE的延长线于E,利用△BNC≌△CED,证得△BPN≌△BQE,即可判断④符合题意;连接N,E,设 ,则 , ,利用勾股定理求出CN,CE的长,然后根据 的面积求出GE,GN,再证 ,利用相似三角形对应边成比例,求出BG,BF的长,即可得⑤符合题意.
6.【答案】2.7
【解析】【解答】解:如图,过 作 于 ,则 ,
∴ ,即 ,
解得 ,
故答案为:2.7
【分析】先求出,再求出,最后求解即可。
7.【答案】4:25
【解析】【解答】∵ ,∴三角尺的面积与它在墙上形成的影子的面积的比= .
【分析】根据物高 :影长可得相似比的值,再根据相似三角形的面积的比等于相似比的平方可求解。
8.【答案】
【解析】【解答】解:如图所示:过点B′作B′F⊥BC,垂足为F,连接B′C.
∵点E是BC的中点,
∴BE= .
在Rt△ABE中,AE= .
由射影定理可知;OE AE=BE2,
∴OE= .
由翻折的性质可知;BO⊥AE.
∴ .
∴OB= .
∴BB′= .
∵∠OBE=∠FBB′,∠BOE=∠BFB′,
∴△BOE∽△BFB′.
∴ ,即 = .
解得: .
∴FC= .
在Rt△B′FC中,B′C= = .
故答案为: .
【分析】先在Rt△ABE中,用勾股定理求得AE,再根据射影定理求得OE,运用△ABE面积的两种表示求得OB的长度,运用△BOE∽△BFB′求得BF,最后在Rt△B′FC中,运用勾股定理求得B′C。
9.【答案】16
【解析】【解答】解:∵,
∴,
∴建筑物的高=16(米)
故答案为:16.
【分析】在同一时刻物高和影长成正比,即在同一时刻的两个物体,影子,经过物体顶部的太阳光线三者构成的三角形相似,根据相似三角形的性质列出等式,即可求出答案.
10.【答案】
【解析】【解答】如图:
根据题意得:BG=AF=AE=1.5m,AB=1m,
∵BG∥AF∥CD
∴△EAF∽△ECD,△ABG∽△ACD,
∴AE:EC=AF:CD,AB:AC=BG:CD,
设BC=xm,CD=ym,则CE=(x+2.5)m,AC=(x+1)m,
则 , ,
解得:x=2,y=4.5,
即CD=4.5米,
故答案为:4.5.
【分析】首先抽象出数学图形,根据平行于三角形一边的直线截其他两边,所截得的三角形与原三角形系数得出△EAF∽△ECD,△ABG∽△ACD,根据相似三角形对应边成比例得出AE:EC=AF:CD,AB:AC=BG:CD,设BC=xm,CD=ym,则CE=(x+2.5)m,AC=(x+1)m,根据比例式建立出方程组,求解即可得出答案。
11.【答案】解:在△ABC与△AMN中,
= , = ,∴ ,又∵∠A=∠A,
∴△ABC∽△AMN,
∴ ,即 ,
解得:MN=1500米,
答:M、N两点之间的直线距离是1500米
【解析】【分析】先根据相似三角形的判定得出△ABC∽△AMN,再利用相似三角形的性质解答即可.
12.【答案】解:如图所示:线段EG表示小明此时的影子;根据题意得:BD=CD=DE=EF=1.6米,AB∥CD,∴BE=3.2米,△CDE∽△ABE,∴ ,即 ,解得:AB=3.2米,同理:△FEG∽△ABG,∴ ,即 ,解得:EG=3.2米;答:此时小明的影长为3.2米.
【解析】【分析】灯A与小明一次所在位置CD的顶端C的连线与地面BD的延长线的相交于点GEG即为所求影子。易得△CDE∽△ABE可求得AB=3.2米,再利用△FEG∽△ABG,可求得小明现在的影长为3.2米。
13.【答案】解:∵EG⊥AB,FH⊥AD,HG经过点A,
∴FA∥EG,EA∥FH,
∴∠AEG=∠HFA=90°,∠EAG=∠FHA,
∴△GEA∽△AFH,
∴ .
∵AB=9里,AD=7里,EG=15里,
∴AF=3.5里,AE=4.5里,
∴ ,
∴FH=1.05里.
【解析】【分析】首先根据题意得到△GEA∽△AFH,然后利用相似三角形的对应边的比相等列出比例式求得答案即可.
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
