2022-2023学年人教版九年级数学上册24.1圆的有关性质 同步达标测试题 (word、含答案)
文档属性
| 名称 | 2022-2023学年人教版九年级数学上册24.1圆的有关性质 同步达标测试题 (word、含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 294.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-20 00:00:00 | ||
图片预览



文档简介
2022-2023学年人教版九年级数学上册《24.1圆的有关性质》同步达标测试题(附答案)
一.选择题(共8小题,满分40分)
1.如图,⊙O中,点A,O,D以及点B,O,C分别在一条直线上,图中弦的条数有( )
A.2条 B.3条 C.4条 D.5条
2.下列说法正确的个数是( )
①直径是圆中最长的弦;②弧是半圆;③过圆心的直线是直径;④半圆不是弧;⑤长度相等的弧是等弧.
A.1个 B.2个 C.3个 D.4个
3.如图所示,⊙O是正方形ABCD的外接圆,P是⊙O上不与A、B重合的任意一点,则∠APB等于( )
A.45° B.60° C.45° 或135° D.60° 或120°
4.如图,⊙O的弦AB、CD相交于点P,若AP=6,BP=8,CP=4,则CD长为( )
A.16 B.24 C.12 D.不能确定
5.如图,在△ABC中,∠C=90°,∠B=28°,以C为圆心,CA为半径的圆交AB于点D,交BC于点E,则弧AD的度数为( )
A.28° B.34° C.56° D.62°
6.如图.已知A、B、C三点在⊙O上,点C在劣弧AB上,且∠AOB=130°,则∠ACB的度数为( )
A.130° B.125° C.120° D.115°
7.如图为某桥的桥拱平面图形,拱宽AB=12,拱高CD为4,则该桥拱所在圆弧的半径为( )
A.4.5 B.5.5 C.6.5 D.7.5
8.“圆材埋壁”是我国古代著名的数学著作《九章算术》中的一个问题,“今有圆材,埋在壁中,不知大小,以锯锯之,深一寸,锯道长一尺,问锯几何?”用现代的数学语言表述是:“如图,CD为⊙O的直径,弦AB⊥CD垂足为E,CE=1寸,AB=10寸,求直径CD的长”,依题意,CD长为( )
A.12寸 B.13寸 C.24寸 D.26寸
二.填空题(共8小题,满分40分)
9.如图,在⊙O中,直径AB∥弦CD,若∠COD=110°,则的度数为 .
10.在同圆中,若,则AB 2CD(填>,<,=).
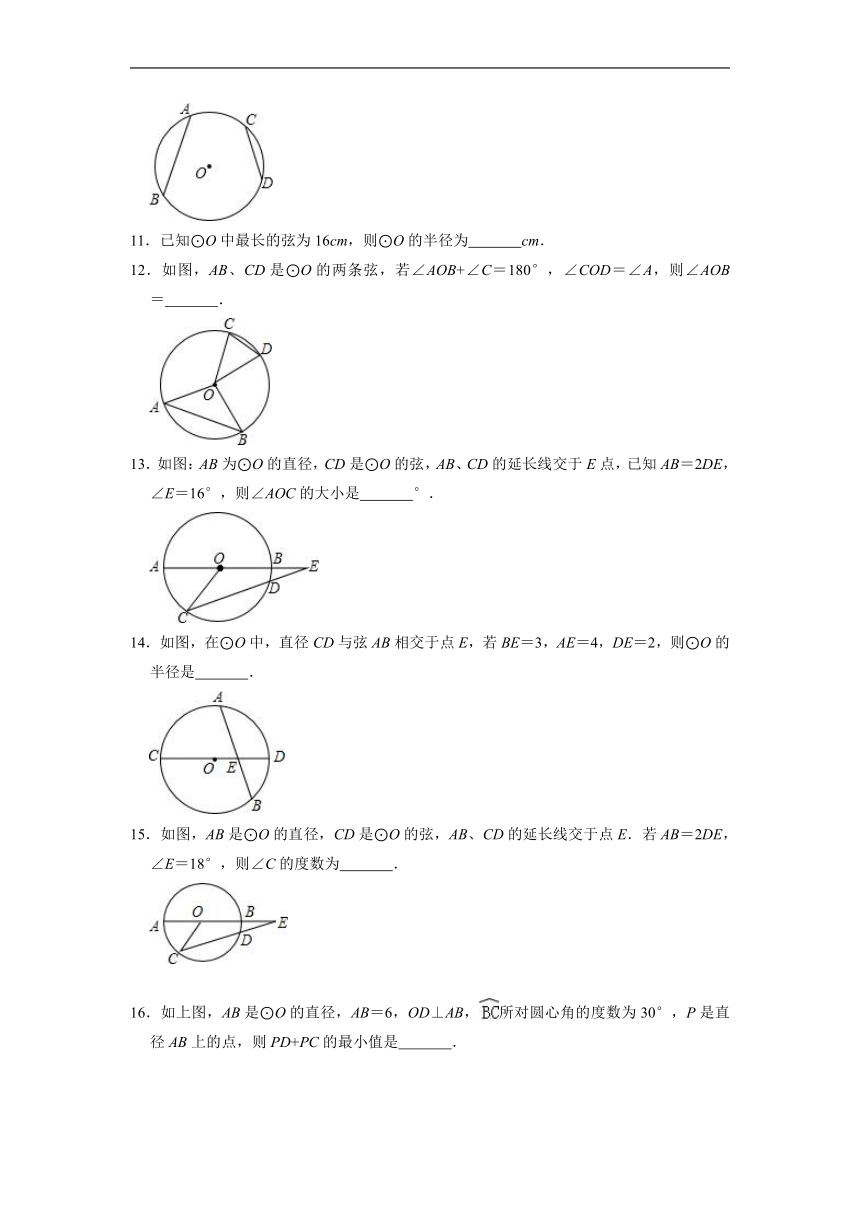
11.已知⊙O中最长的弦为16cm,则⊙O的半径为 cm.
12.如图,AB、CD是⊙O的两条弦,若∠AOB+∠C=180°,∠COD=∠A,则∠AOB= .
13.如图:AB为⊙O的直径,CD是⊙O的弦,AB、CD的延长线交于E点,已知AB=2DE,∠E=16°,则∠AOC的大小是 °.
14.如图,在⊙O中,直径CD与弦AB相交于点E,若BE=3,AE=4,DE=2,则⊙O的半径是 .
15.如图,AB是⊙O的直径,CD是⊙O的弦,AB、CD的延长线交于点E.若AB=2DE,∠E=18°,则∠C的度数为 .
16.如上图,AB是⊙O的直径,AB=6,OD⊥AB,所对圆心角的度数为30°,P是直径AB上的点,则PD+PC的最小值是 .
三.解答题(共6小题,满分40分)
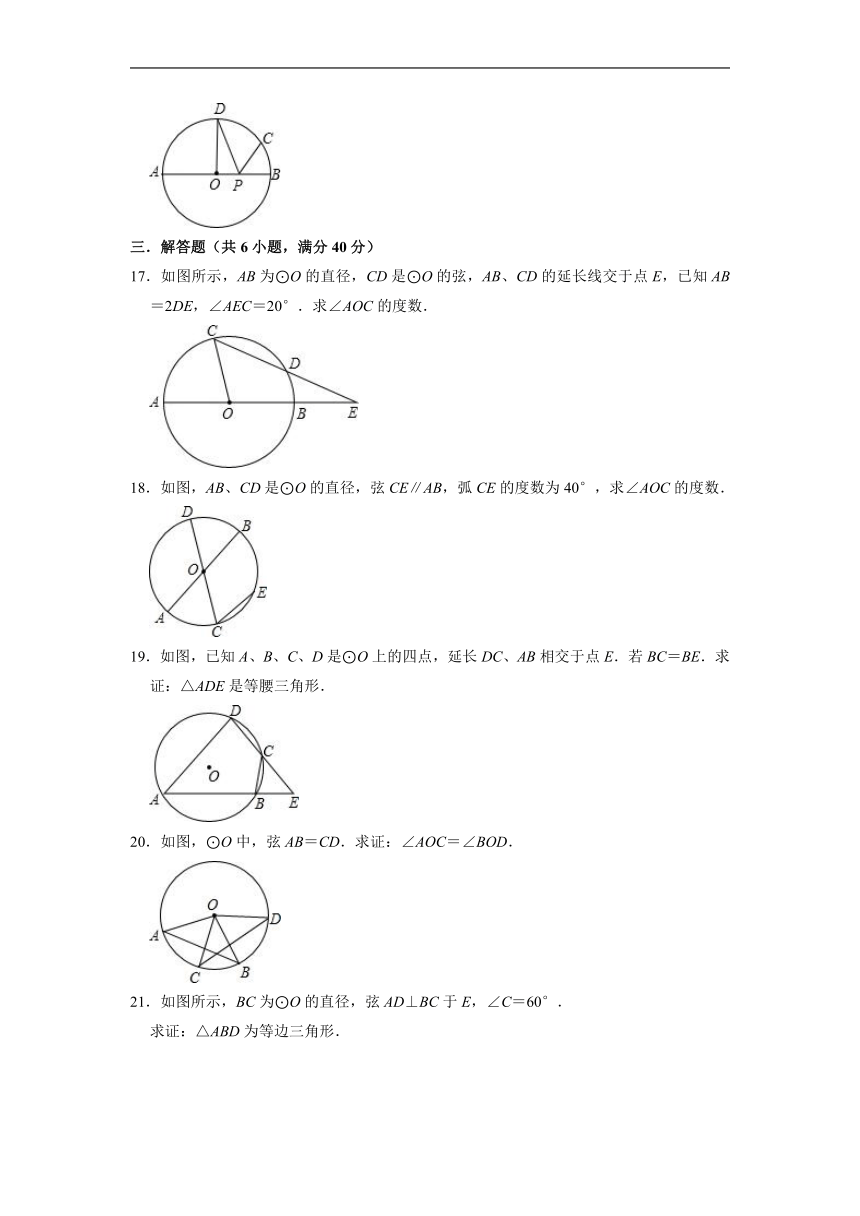
17.如图所示,AB为⊙O的直径,CD是⊙O的弦,AB、CD的延长线交于点E,已知AB=2DE,∠AEC=20°.求∠AOC的度数.
18.如图,AB、CD是⊙O的直径,弦CE∥AB,弧CE的度数为40°,求∠AOC的度数.
19.如图,已知A、B、C、D是⊙O上的四点,延长DC、AB相交于点E.若BC=BE.求证:△ADE是等腰三角形.
20.如图,⊙O中,弦AB=CD.求证:∠AOC=∠BOD.
21.如图所示,BC为⊙O的直径,弦AD⊥BC于E,∠C=60°.
求证:△ABD为等边三角形.
22.如图,在⊙O中,DE是⊙O的直径,AB是⊙O的弦,AB的中点C在直径DE上.已知AB=8cm,CD=2cm.
(1)求⊙O的面积;
(2)连接AE,过圆心O向AE作垂线,垂足为F,求OF的长.
参考答案
一.选择题(共8小题,满分40分)
1.解:图中的弦有AB,BC,CE共三条,
故选:B.
2.解:直径是圆中最长的弦,所以①正确;
弧不一定是半圆,所以②错误;
过圆心的弦是直径,所以③错误;
半圆是弧,所以④错误;
在同圆或等圆中,长度相等的弧是等弧,所以⑤错误.
故选:A.
3.解:连接OA,OB,
∵⊙O是正方形ABCD的外接圆,
∴∠AOB=90°,
若点P在优弧ADB上,则∠APB=∠AOB=45°;
若点P在劣弧AB上,
则∠APB=180°﹣45°=135°.
∴∠APB=45°或135°.
故选:C.
4.解:∵AP BP=CP DP,
∴PD=,
∵AP=6,BP=8,CP=4,
∴PD=12,
∴CD=PC+PD=12+4=16.
故选:A.
5.解:∵在△ABC中,∠ACB=90°,∠B=28°
∴∠A=90°﹣∠B=62度.
∵CA=CD
∴∠CDA=∠CAD=62°
∴∠ACD=56°
故选:C.
6.解:在优弧上取一点D,连接AD、BD,
∠D=∠AOB=65°,
∵四边形ADBC是⊙O的内接四边形,
∴∠D+∠ACB=180°,
∴∠ACB=115°,
故选:D.
7.解:∵OC⊥AB,OC过O,
∴根据垂径定理得:AD=BD=6,
∵在Rt△ADO中,AD2+OD2=AO2,
∴62+(R﹣4)2=R2,
解得:R=6.5,
故选:C.
8.解:连接OA,如图所示,
设直径CD的长为2x,则半径OC=x,
∵CD为⊙O的直径,弦AB⊥CD于E,AB=10寸,
∴AE=BE=AB=×10=5寸,
连接OA,则OA=x寸,
根据勾股定理得x2=52+(x﹣1)2,
解得x=13,
CD=2x=2×13=26(寸).
故选:D.
二.填空题(共8小题,满分40分)
9.解:∵OC=OD,
∴∠C=∠D,
∴∠C=(180°﹣∠COD)=×(180°﹣110°)=35°,
∵CD∥AB,
∴∠AOC=∠C=35°,
∴的度数为35°.
故答案为35°.
10.解:找出的中点E,连接AE、BE,
∵的中点E,
∴==,
∵,
∴==,
∴AE=EB=CD,
∵AE+EB>AB,
∴AB<2CD,
故答案为:<.
11.解:∵⊙O中最长的弦为16cm,即直径为16cm,
∴⊙O的半径为8cm.
故答案为:8.
12.解:设∠COD=∠A=x°,
∴∠AOB=(180﹣2x)°,
∠OCD=∠ODC=°,
∵∠AOB+∠C=180°,
∴+180﹣2x=180
解得:x=36
∴∠AOB=(180﹣2x)°=108°,
故答案为:108°.
13.解:连接OD,如图,
∵AB=2DE,
∴DE=DO,
∴∠E=∠DOE=16°,
∴∠CDO=∠E+∠DOE=32°,
∵OC=OD,
∴∠C=∠CDO=32°,
∴∠AOC=∠C+∠E=32°+16°=48°.
故答案为48.
14.解:根据相交弦定理,AE BE=CE DE,
又∵BE=3,AE=4,DE=2,
∴CE=6
∴CD=CE+DE=8
那么圆的半径等于4.
故答案为:4.
15.解:连接OD,∵AB=2DE,
∴OD=DE,
∴∠E=∠EOD,
在△EDO中,∠ODC=∠E+∠EOD=36°,
∵OC=OD,
∴∠C=∠ODC=36°.
故答案为:36°.
16.解:作C点关于AB的对称点C′,连DC′交AB于P点,过D点作直径DE,连EC′,OC、OC′,如图,
∵所对圆心角的度数为30°,
即∠BOC=30°,
∴∠BOC′=30°,PC=PC′,
∴DC′是PD+PC的最小值.
又∵∠EOC′=90°﹣30°=60°,
∴∠D=30°,
而DE=AB=6,
在Rt△DEC′中,EC′=AB=3,DC′=EC′=3.
即PD+PC的最小值是3.
故答案为3.
三.解答题(共6小题,满分40分)
17.解:连接OD,如图,
∵AB=2DE,
而AB=2OD,
∴OD=DE,
∴∠DOE=∠E=20°,
∴∠CDO=∠DOE+∠E=40°,
而OC=OD,
∴∠C=∠ODC=40°,
∴∠AOC=∠C+∠E=60°.
18.解:连接OE,如图,
∵弧CE的度数为40°,
∴∠COE=40°,
∵OC=OE,
∴∠OCE=∠OEC,
∴∠OCE=(180°﹣40°)÷2=70°,
∵弦CE∥AB,
∴∠AOC=∠OCE=70°.
19.证明:∵A、D、C、B四点共圆,
∴∠A=∠BCE,
∵BC=BE,
∴∠BCE=∠E,
∴∠A=∠E,
∴AD=DE,
即△ADE是等腰三角形.
20.解:∵弦AB=CD(已知),
∴=;
∴∠AOB=∠COD,
∴∠AOB﹣∠BOC=∠COD﹣∠BOC,
即∠AOC=∠BOD.
21.证明:∵BC为⊙O的直径,AD⊥BC,
∴AE=DE,
∴BD=BA,
∵∠D=∠C=60°,
∴△ABD为等边三角形.
22.解:(1)连接OA,如图1所示.
∵C为AB的中点,AB=8cm,
∴AC=4cm.
又∵CD=2cm,
设⊙O的半径为rcm,则(r﹣2)2+42=r2.
解得:r=5.
∴S=πr2=π×25=25π(cm );
(2)OC=OD﹣CD=5﹣2=3(cm),
EC=EO+OC=5+3=8(cm),
∴EA===4(cm).
∴EF===2(cm).
∴OF===(cm).
一.选择题(共8小题,满分40分)
1.如图,⊙O中,点A,O,D以及点B,O,C分别在一条直线上,图中弦的条数有( )
A.2条 B.3条 C.4条 D.5条
2.下列说法正确的个数是( )
①直径是圆中最长的弦;②弧是半圆;③过圆心的直线是直径;④半圆不是弧;⑤长度相等的弧是等弧.
A.1个 B.2个 C.3个 D.4个
3.如图所示,⊙O是正方形ABCD的外接圆,P是⊙O上不与A、B重合的任意一点,则∠APB等于( )
A.45° B.60° C.45° 或135° D.60° 或120°
4.如图,⊙O的弦AB、CD相交于点P,若AP=6,BP=8,CP=4,则CD长为( )
A.16 B.24 C.12 D.不能确定
5.如图,在△ABC中,∠C=90°,∠B=28°,以C为圆心,CA为半径的圆交AB于点D,交BC于点E,则弧AD的度数为( )
A.28° B.34° C.56° D.62°
6.如图.已知A、B、C三点在⊙O上,点C在劣弧AB上,且∠AOB=130°,则∠ACB的度数为( )
A.130° B.125° C.120° D.115°
7.如图为某桥的桥拱平面图形,拱宽AB=12,拱高CD为4,则该桥拱所在圆弧的半径为( )
A.4.5 B.5.5 C.6.5 D.7.5
8.“圆材埋壁”是我国古代著名的数学著作《九章算术》中的一个问题,“今有圆材,埋在壁中,不知大小,以锯锯之,深一寸,锯道长一尺,问锯几何?”用现代的数学语言表述是:“如图,CD为⊙O的直径,弦AB⊥CD垂足为E,CE=1寸,AB=10寸,求直径CD的长”,依题意,CD长为( )
A.12寸 B.13寸 C.24寸 D.26寸
二.填空题(共8小题,满分40分)
9.如图,在⊙O中,直径AB∥弦CD,若∠COD=110°,则的度数为 .
10.在同圆中,若,则AB 2CD(填>,<,=).
11.已知⊙O中最长的弦为16cm,则⊙O的半径为 cm.
12.如图,AB、CD是⊙O的两条弦,若∠AOB+∠C=180°,∠COD=∠A,则∠AOB= .
13.如图:AB为⊙O的直径,CD是⊙O的弦,AB、CD的延长线交于E点,已知AB=2DE,∠E=16°,则∠AOC的大小是 °.
14.如图,在⊙O中,直径CD与弦AB相交于点E,若BE=3,AE=4,DE=2,则⊙O的半径是 .
15.如图,AB是⊙O的直径,CD是⊙O的弦,AB、CD的延长线交于点E.若AB=2DE,∠E=18°,则∠C的度数为 .
16.如上图,AB是⊙O的直径,AB=6,OD⊥AB,所对圆心角的度数为30°,P是直径AB上的点,则PD+PC的最小值是 .
三.解答题(共6小题,满分40分)
17.如图所示,AB为⊙O的直径,CD是⊙O的弦,AB、CD的延长线交于点E,已知AB=2DE,∠AEC=20°.求∠AOC的度数.
18.如图,AB、CD是⊙O的直径,弦CE∥AB,弧CE的度数为40°,求∠AOC的度数.
19.如图,已知A、B、C、D是⊙O上的四点,延长DC、AB相交于点E.若BC=BE.求证:△ADE是等腰三角形.
20.如图,⊙O中,弦AB=CD.求证:∠AOC=∠BOD.
21.如图所示,BC为⊙O的直径,弦AD⊥BC于E,∠C=60°.
求证:△ABD为等边三角形.
22.如图,在⊙O中,DE是⊙O的直径,AB是⊙O的弦,AB的中点C在直径DE上.已知AB=8cm,CD=2cm.
(1)求⊙O的面积;
(2)连接AE,过圆心O向AE作垂线,垂足为F,求OF的长.
参考答案
一.选择题(共8小题,满分40分)
1.解:图中的弦有AB,BC,CE共三条,
故选:B.
2.解:直径是圆中最长的弦,所以①正确;
弧不一定是半圆,所以②错误;
过圆心的弦是直径,所以③错误;
半圆是弧,所以④错误;
在同圆或等圆中,长度相等的弧是等弧,所以⑤错误.
故选:A.
3.解:连接OA,OB,
∵⊙O是正方形ABCD的外接圆,
∴∠AOB=90°,
若点P在优弧ADB上,则∠APB=∠AOB=45°;
若点P在劣弧AB上,
则∠APB=180°﹣45°=135°.
∴∠APB=45°或135°.
故选:C.
4.解:∵AP BP=CP DP,
∴PD=,
∵AP=6,BP=8,CP=4,
∴PD=12,
∴CD=PC+PD=12+4=16.
故选:A.
5.解:∵在△ABC中,∠ACB=90°,∠B=28°
∴∠A=90°﹣∠B=62度.
∵CA=CD
∴∠CDA=∠CAD=62°
∴∠ACD=56°
故选:C.
6.解:在优弧上取一点D,连接AD、BD,
∠D=∠AOB=65°,
∵四边形ADBC是⊙O的内接四边形,
∴∠D+∠ACB=180°,
∴∠ACB=115°,
故选:D.
7.解:∵OC⊥AB,OC过O,
∴根据垂径定理得:AD=BD=6,
∵在Rt△ADO中,AD2+OD2=AO2,
∴62+(R﹣4)2=R2,
解得:R=6.5,
故选:C.
8.解:连接OA,如图所示,
设直径CD的长为2x,则半径OC=x,
∵CD为⊙O的直径,弦AB⊥CD于E,AB=10寸,
∴AE=BE=AB=×10=5寸,
连接OA,则OA=x寸,
根据勾股定理得x2=52+(x﹣1)2,
解得x=13,
CD=2x=2×13=26(寸).
故选:D.
二.填空题(共8小题,满分40分)
9.解:∵OC=OD,
∴∠C=∠D,
∴∠C=(180°﹣∠COD)=×(180°﹣110°)=35°,
∵CD∥AB,
∴∠AOC=∠C=35°,
∴的度数为35°.
故答案为35°.
10.解:找出的中点E,连接AE、BE,
∵的中点E,
∴==,
∵,
∴==,
∴AE=EB=CD,
∵AE+EB>AB,
∴AB<2CD,
故答案为:<.
11.解:∵⊙O中最长的弦为16cm,即直径为16cm,
∴⊙O的半径为8cm.
故答案为:8.
12.解:设∠COD=∠A=x°,
∴∠AOB=(180﹣2x)°,
∠OCD=∠ODC=°,
∵∠AOB+∠C=180°,
∴+180﹣2x=180
解得:x=36
∴∠AOB=(180﹣2x)°=108°,
故答案为:108°.
13.解:连接OD,如图,
∵AB=2DE,
∴DE=DO,
∴∠E=∠DOE=16°,
∴∠CDO=∠E+∠DOE=32°,
∵OC=OD,
∴∠C=∠CDO=32°,
∴∠AOC=∠C+∠E=32°+16°=48°.
故答案为48.
14.解:根据相交弦定理,AE BE=CE DE,
又∵BE=3,AE=4,DE=2,
∴CE=6
∴CD=CE+DE=8
那么圆的半径等于4.
故答案为:4.
15.解:连接OD,∵AB=2DE,
∴OD=DE,
∴∠E=∠EOD,
在△EDO中,∠ODC=∠E+∠EOD=36°,
∵OC=OD,
∴∠C=∠ODC=36°.
故答案为:36°.
16.解:作C点关于AB的对称点C′,连DC′交AB于P点,过D点作直径DE,连EC′,OC、OC′,如图,
∵所对圆心角的度数为30°,
即∠BOC=30°,
∴∠BOC′=30°,PC=PC′,
∴DC′是PD+PC的最小值.
又∵∠EOC′=90°﹣30°=60°,
∴∠D=30°,
而DE=AB=6,
在Rt△DEC′中,EC′=AB=3,DC′=EC′=3.
即PD+PC的最小值是3.
故答案为3.
三.解答题(共6小题,满分40分)
17.解:连接OD,如图,
∵AB=2DE,
而AB=2OD,
∴OD=DE,
∴∠DOE=∠E=20°,
∴∠CDO=∠DOE+∠E=40°,
而OC=OD,
∴∠C=∠ODC=40°,
∴∠AOC=∠C+∠E=60°.
18.解:连接OE,如图,
∵弧CE的度数为40°,
∴∠COE=40°,
∵OC=OE,
∴∠OCE=∠OEC,
∴∠OCE=(180°﹣40°)÷2=70°,
∵弦CE∥AB,
∴∠AOC=∠OCE=70°.
19.证明:∵A、D、C、B四点共圆,
∴∠A=∠BCE,
∵BC=BE,
∴∠BCE=∠E,
∴∠A=∠E,
∴AD=DE,
即△ADE是等腰三角形.
20.解:∵弦AB=CD(已知),
∴=;
∴∠AOB=∠COD,
∴∠AOB﹣∠BOC=∠COD﹣∠BOC,
即∠AOC=∠BOD.
21.证明:∵BC为⊙O的直径,AD⊥BC,
∴AE=DE,
∴BD=BA,
∵∠D=∠C=60°,
∴△ABD为等边三角形.
22.解:(1)连接OA,如图1所示.
∵C为AB的中点,AB=8cm,
∴AC=4cm.
又∵CD=2cm,
设⊙O的半径为rcm,则(r﹣2)2+42=r2.
解得:r=5.
∴S=πr2=π×25=25π(cm );
(2)OC=OD﹣CD=5﹣2=3(cm),
EC=EO+OC=5+3=8(cm),
∴EA===4(cm).
∴EF===2(cm).
∴OF===(cm).
同课章节目录
