2022-2023学年人教版九年级数学上册24.1圆的有关性质 自主达标测试题(word、含解析)
文档属性
| 名称 | 2022-2023学年人教版九年级数学上册24.1圆的有关性质 自主达标测试题(word、含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 262.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-20 15:46:38 | ||
图片预览




文档简介
2022-2023学年人教版九年级数学上册《24.1圆的有关性质》自主达标测试题(附答案)
一.选择题(共8小题,满分40分)
1.如图,在⊙O中,弦的条数是( )
A.2 B.3 C.4 D.以上均不正确
2.如图,半径为5的⊙A中,弦BC,ED所对的圆心角分别是∠BAC,∠EAD,若DE=6,∠BAC+∠EAD=180°,则弦BC的长等于( )
A.8 B.10 C.11 D.12
3.如图,在⊙O中,弦AB为8mm,圆心O到AB的距离为3mm,则⊙O的半径等于( )
A.3mm B.4mm C.5mm D.8mm
4.下列说法中正确的个数有( )
①相等的圆心角所对的弧相等;②平分弦的直径一定垂直于弦;
③圆是轴对称图形,每一条直径都是对称轴;④直径是弦;⑤长度相等的弧是等弧.
A.1个 B.2个 C.3个 D.4个
5.如图,四边形ABCD内接于⊙O.∠B=α,则∠D的度数为( )
A.90°+α B.90°﹣α C.180°+α D.180°﹣α
6.如图,⊙O的弦AB、CD相交于点P,若AP=3,BP=4,CP=2,则CD长为( )
A.6 B.12 C.8 D.不能确定
7.如图,AB为⊙O的直径,CD为⊙O的弦,若∠CAB=51°,则∠ADC的度数为( )
A.45° B.35° C.42° D.39°
8.《九章算术》是我国古代第一部自成体系的数学专著,代表了东方数学的最高成就.它的算法体系至今仍在推动着计算机的发展和应用.书中记载:“今有圆材埋在壁中,不知大小,以锯锯之,深一寸,锯道长一尺,问径几何?”译为:“今有一圆柱形木材,埋在墙壁中,不知其大小,用锯去锯这木材,锯口深1寸(ED=1寸),锯道长1尺(AB=1尺=10寸)”,问这块圆柱形木材的直径是多少?”
如图所示,请根据所学知识计算:圆柱形木材的直径AC是( )
A.13寸 B.20寸 C.26寸 D.28寸
二.填空题(共6小题,满分30分)
9.如图,⊙O的半径为10cm,AB是⊙O的弦,OC⊥AB于D,交⊙O于点C,且CD=4cm,弦AB的长为 cm.
10.把球放在长方体纸盒内,球的一部分露出盒外,其截面如图所示,已知EF=CD=4cm,则球的半径为 cm.
11.一个圆的半径为2,弦长是2,求这条弦所对的圆周角是 .
12.利用圆周角定理,我们可以得到圆内接四边形的一个性质,请规范写出我们所学的这个性质的内容 ,并利用这个性质完成下题:如图,四边形ABCD内接于⊙O,若∠A=60°,则∠DCE的度数是 .
13.如图,CD是⊙O的直径,∠EOD=84°,AE交⊙O于点B,且AB=OC,则∠A的度数是 .
14.如图,⊙O的动弦AB,CD相交于点E,且AB=CD,∠BED=α(0°<α<90°).在①∠BOD=α,②∠OAB=90°﹣α,③∠ABC=α中,一定成立的是 (填序号).
三.解答题(共7小题,满分50分)
15.如图,已知AB是⊙O的直径,C是⊙O上的一点,CD⊥AB于D,AD<BD,若CD=2cm,AB=5cm,求AD、AC的长.
16.如图,在⊙O中,AD=BC,求证:DC=AB.
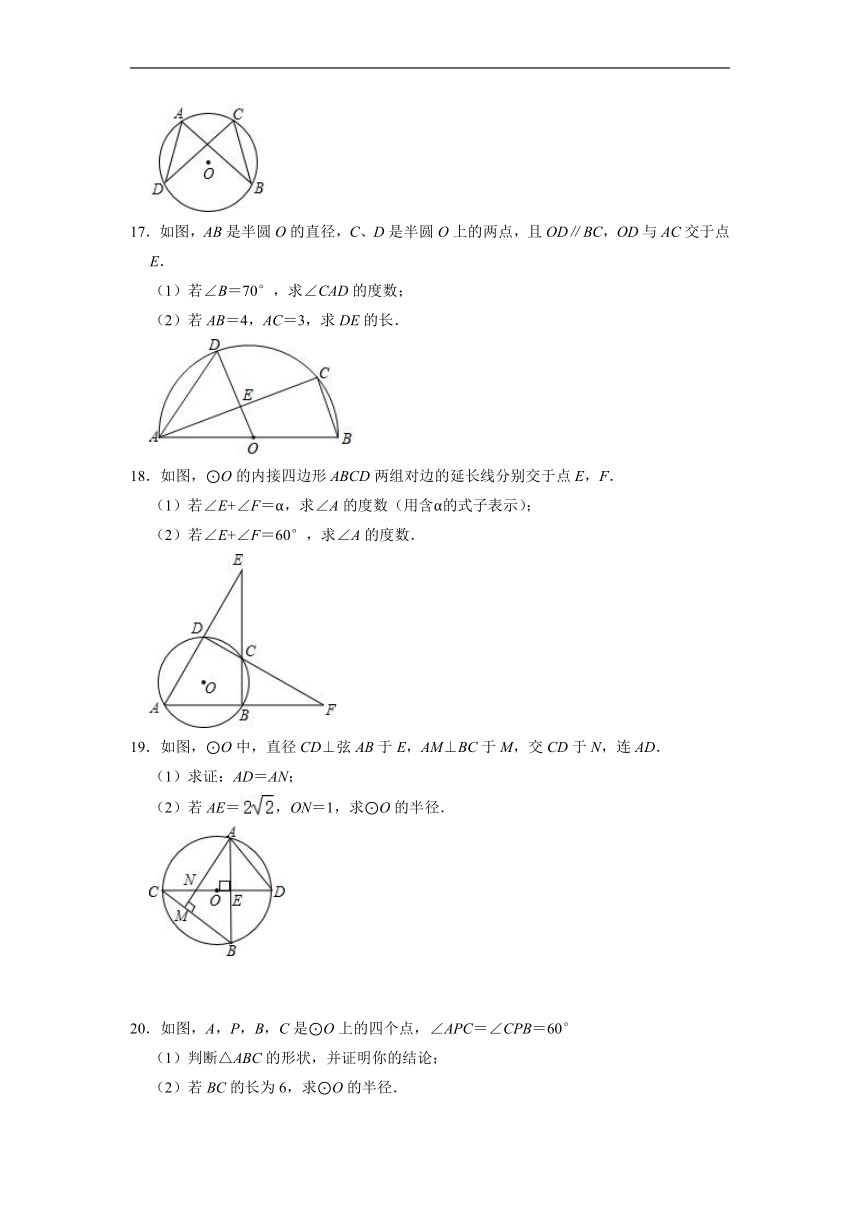
17.如图,AB是半圆O的直径,C、D是半圆O上的两点,且OD∥BC,OD与AC交于点E.
(1)若∠B=70°,求∠CAD的度数;
(2)若AB=4,AC=3,求DE的长.
18.如图,⊙O的内接四边形ABCD两组对边的延长线分别交于点E,F.
(1)若∠E+∠F=α,求∠A的度数(用含α的式子表示);
(2)若∠E+∠F=60°,求∠A的度数.
19.如图,⊙O中,直径CD⊥弦AB于E,AM⊥BC于M,交CD于N,连AD.
(1)求证:AD=AN;
(2)若AE=,ON=1,求⊙O的半径.
20.如图,A,P,B,C是⊙O上的四个点,∠APC=∠CPB=60°
(1)判断△ABC的形状,并证明你的结论;
(2)若BC的长为6,求⊙O的半径.
21.如图,四边形ABCD是⊙O的内接四边形,点F是CD延长线上的一点,且AD平分∠BDF,AE⊥CD于点E.
(1)求证:AB=AC.
(2)若BD=11,DE=2,求CD的长.
参考答案
一.选择题(共8小题,满分40分)
1.解:如图,在⊙O中,有弦AB、弦DB、弦CB、弦CD.共有4条弦.
故选:C.
2.解:作直径CF,连接BF,如图,
则∠FBC=90°,
∵∠BAC+∠EAD=180°,
而∠BAC+∠BAF=180°,
∴∠DAE=∠BAF,
∴=,
∴DE=BF=6,
∴BC==8.
解法二:如图,过点A作AM⊥BC于M,AN⊥DE于N.
∵AM⊥BC,AN⊥DE,
∴CM=MB,DN=NE=3,
∵AC=AB=AD=AE,
∴∠BAC=2∠MAC,∠EAD=2∠DAN,
∵∠BAC+∠EAD=180°,
∴2∠CAM+2∠DAN=180°,
∴∠CAM+∠DAN=90°,
∵∠ACM+∠CAM=90°,
∴∠ACM=∠DAN,
∵∠AMC=∠AND=90°,
∴△AMC≌△DNA(AAS),
∴AM=DN=3,
∴CM===4,
∴BC=2CM=8.
故选:A.
3.解:连接OA,
∵OD⊥AB,
∴AD=AB=4(mm),
由勾股定理得,OA==5(mm),
故选:C.
4.解:①相等的圆心角所对的弧相等;错误.必须在同圆或等圆中;
②平分弦的直径一定垂直于弦;错误,此弦不是直径;
③圆是轴对称图形,每一条直径都是对称轴;错误,应该是每一条直径所在的直线都是对称轴;
④直径是弦;正确;
⑤长度相等的弧是等弧.错误.能够完全重合的两条弧是等弧;
故选:A.
5.解:∵四边形ABCD内接于⊙O,
∴∠D+∠B=180°,
又∠B=α,
∴∠D=180°﹣∠B=180°﹣α.
故选:D.
6.解:∵AP BP=CP DP,
∴PD=,
∵AP=3,BP=4,CP=2,
∴PD=6,
∴CD=PC+PD=2+6=8.
故选:C.
7.解:如图,连接BD,
∴∠CDB=∠CAB=51°,
∵AB是⊙O的直径,
∴∠ADB=90°,
∴∠ADC=90°﹣∠CDB=39°,
故选:D.
8.解:设⊙O的半径为r寸.
在Rt△ADO中,AD=5寸,OD=(r﹣1)寸,OA=r寸,
则有r2=52+(r﹣1)2,
解得r=13,
∴⊙O的直径为26寸,
故选:C.
二.填空题(共6小题,满分30分)
9.解:连接OA,
∵OA=OC=10cm,CD=4cm,
∴OD=10﹣4=6cm,
在Rt△OAD中,有勾股定理得:AD==8cm,
∵OC⊥AB,OC过O,
∴AB=2AD=16cm.
故答案为16.
10.解:EF的中点M,作MN⊥AD于点M,取MN上的球心O,连接OF,
∵四边形ABCD是矩形,
∴∠C=∠D=90°,
∴四边形CDMN是矩形,
∴MN=CD=4,
设OF=x,则ON=OF,
∴OM=MN﹣ON=4﹣x,MF=2,
在直角三角形OMF中,OM2+MF2=OF2
即:(4﹣x)2+22=x2
解得:x=2.5
故答案为:2.5
11.解:连接OA,过点O作OD⊥AB于点D,
∵OA=2,AB=2,
∴AD=BD=2,
∴AD:OA=:2,
∴∠AOD=60°,
∴∠AOB=120°,
∴∠AMB=60°,
∴∠ANB=120°.
故答案为:60°或120°.
12.解:∵圆内接四边形的对角互补,
∴∠A+∠BCD=180°,
∵∠A=60°,
∴∠BCD=120°,
∴∠DCE=180°﹣∠BCD=60°,
故答案为;圆内接四边形的对角互补,60°.
13.解:由AB=OC,得
AB=OB,
∠A=∠AOB.
由BO=EO,得
∠BEO=∠EBO.
由∠EBO是△ABO的外角,得
∠EBO=∠A+∠AOB=2∠A,
∠BEO=∠EBO=2∠A.
由∠DOE是△AOE的外角,得
∠A+∠AEO=∠EOD,
即∠A+2∠A=84°,
∠A=28°.
故答案为:28°.
14.解:如图,连接OC,设OB交CD于K.
∵AB=CD,OD=OC=OB=OA,
∴△AOB≌△COD(SSS),
∴∠CDO=∠OBA,
∵∠DKO=∠BKE,
∴∠DOK=∠BEK=α,
即∠BOD=α,故①正确,
不妨设,∠OAB=90°﹣α,
∵OA=OB,
∴∠OAB=∠OBA,
∴∠OBE+∠BEK=90°,
∴∠BKE=90°,
∴OB⊥CD,从条件上看,AB=CD,推不出OB⊥CD这样的位置关系,故②错误,
∵CD=AB,
∴=,
∴=,
∴∠ABC=∠DOB=α,故③正确.
故答案为①③.
三.解答题(共7小题,满分50分)
15.解:连接OC,
∵AB=5cm,
∴OC=OA=AB=cm,
Rt△CDO中,由勾股定理得:DO==cm,
∴AD=﹣=1cm,
由勾股定理得:AC==,
则AD的长为1cm,AC的长为cm.
16.证明:∵AD=BC,
∴=,
∴+=+,
即=,
∴DC=AB.
17.解:(1)∵AB是半圆O的直径,
∴∠ACB=90°,
又∵OD∥BC,
∴∠AEO=90°,即OE⊥AC,
∠CAB=90°﹣∠B=90°﹣70°=20°,∠AOD=∠B=70°.
∵OA=OD,
∴∠DAO=∠ADO=(180°﹣∠AOD)=(180°﹣70°)=55°,
∴∠CAD=∠DAO﹣∠CAB=55°﹣20°=35°;
(2)在直角△ABC中,BC===.
∵OE⊥AC,
∴AE=EC,
又∵OA=OB,
∴OE=BC=.
又∵OD=AB=2,
∴DE=OD﹣OE=2﹣.
18.解:(1)∵四边形ABCD为⊙O的内接四边形,
∴∠A=∠BCF,
∵∠EBF=∠A+∠E,
而∠EBF=180°﹣∠BCF﹣∠F,
∴∠A+∠E=180°﹣∠BCF﹣∠F,
∴∠A+∠E=180﹣∠A﹣∠F,
即2∠A=180°﹣(∠E+∠F),
∵∠E+∠F=α,
∴∠A=90°﹣α;
(2)当α=60°时,∠A=90°﹣×60°=60°.
19.(1)证明:∵∠BAD与∠BCD是同弧所对的圆周角,
∴∠BAD=∠BCD,
∵AE⊥CD,AM⊥BC,
∴∠AMC=∠AEN=90°,
∵∠ANE=∠CNM,
∴∠BCD=∠BAM,
∴∠BAM=BAD,
在△ANE与△ADE中,
,
∴△ANE≌△ADE,
∴AD=AN;
(2)∵AE=2,AE⊥CD,
又∵ON=1,
∴设NE=x,则OE=x﹣1,NE=ED=x,
r=OD=OE+ED=2x﹣1
连接AO,则AO=OD=2x﹣1,
∵△AOE是直角三角形,AE=2,OE=x﹣1,AO=2x﹣1,
∴(2)2+(x﹣1)2=(2x﹣1)2,
解得x=2,
∴r=2x﹣1=3;
20.解:(1)△ABC是等边三角形,
理由如下:由圆周角定理得,∠ABC=∠APC=60°,∠CAB=∠CPB=60°,
∴△ABC是等边三角形;
(2)延长BO交⊙O于E,连接CE,
由圆周角定理得,∠E=∠BAC=60°,
∴BE=4,
∴⊙O的半径为2.
21.(1)证明:∵AD平分∠BDF,
∴∠ADF=∠ADB,
∵∠ABC+∠ADC=180°,∠ADC+∠ADF=180°,
∴∠ADF=∠ABC,
∵∠ACB=∠ADB,
∴∠ABC=∠ACB,
∴AB=AC;
(2)解:过点A作AG⊥BD,垂足为点G.
∵AD平分∠BDF,AE⊥CF,AG⊥BD,
∴AG=AE,∠AGB=∠AEC=90°,
在Rt△AED和Rt△AGD中,
,
∴Rt△AED≌Rt△AGD,
∴GD=ED=2,
在Rt△AEC和Rt△AGB中,
,
∴Rt△AEC≌Rt△AGB(HL),
∴BG=CE,
∵BD=11,
∴BG=BD﹣GD=11﹣2=9,
∴CE=BG=9,
∴CD=CE﹣DE=9﹣2=7.
一.选择题(共8小题,满分40分)
1.如图,在⊙O中,弦的条数是( )
A.2 B.3 C.4 D.以上均不正确
2.如图,半径为5的⊙A中,弦BC,ED所对的圆心角分别是∠BAC,∠EAD,若DE=6,∠BAC+∠EAD=180°,则弦BC的长等于( )
A.8 B.10 C.11 D.12
3.如图,在⊙O中,弦AB为8mm,圆心O到AB的距离为3mm,则⊙O的半径等于( )
A.3mm B.4mm C.5mm D.8mm
4.下列说法中正确的个数有( )
①相等的圆心角所对的弧相等;②平分弦的直径一定垂直于弦;
③圆是轴对称图形,每一条直径都是对称轴;④直径是弦;⑤长度相等的弧是等弧.
A.1个 B.2个 C.3个 D.4个
5.如图,四边形ABCD内接于⊙O.∠B=α,则∠D的度数为( )
A.90°+α B.90°﹣α C.180°+α D.180°﹣α
6.如图,⊙O的弦AB、CD相交于点P,若AP=3,BP=4,CP=2,则CD长为( )
A.6 B.12 C.8 D.不能确定
7.如图,AB为⊙O的直径,CD为⊙O的弦,若∠CAB=51°,则∠ADC的度数为( )
A.45° B.35° C.42° D.39°
8.《九章算术》是我国古代第一部自成体系的数学专著,代表了东方数学的最高成就.它的算法体系至今仍在推动着计算机的发展和应用.书中记载:“今有圆材埋在壁中,不知大小,以锯锯之,深一寸,锯道长一尺,问径几何?”译为:“今有一圆柱形木材,埋在墙壁中,不知其大小,用锯去锯这木材,锯口深1寸(ED=1寸),锯道长1尺(AB=1尺=10寸)”,问这块圆柱形木材的直径是多少?”
如图所示,请根据所学知识计算:圆柱形木材的直径AC是( )
A.13寸 B.20寸 C.26寸 D.28寸
二.填空题(共6小题,满分30分)
9.如图,⊙O的半径为10cm,AB是⊙O的弦,OC⊥AB于D,交⊙O于点C,且CD=4cm,弦AB的长为 cm.
10.把球放在长方体纸盒内,球的一部分露出盒外,其截面如图所示,已知EF=CD=4cm,则球的半径为 cm.
11.一个圆的半径为2,弦长是2,求这条弦所对的圆周角是 .
12.利用圆周角定理,我们可以得到圆内接四边形的一个性质,请规范写出我们所学的这个性质的内容 ,并利用这个性质完成下题:如图,四边形ABCD内接于⊙O,若∠A=60°,则∠DCE的度数是 .
13.如图,CD是⊙O的直径,∠EOD=84°,AE交⊙O于点B,且AB=OC,则∠A的度数是 .
14.如图,⊙O的动弦AB,CD相交于点E,且AB=CD,∠BED=α(0°<α<90°).在①∠BOD=α,②∠OAB=90°﹣α,③∠ABC=α中,一定成立的是 (填序号).
三.解答题(共7小题,满分50分)
15.如图,已知AB是⊙O的直径,C是⊙O上的一点,CD⊥AB于D,AD<BD,若CD=2cm,AB=5cm,求AD、AC的长.
16.如图,在⊙O中,AD=BC,求证:DC=AB.
17.如图,AB是半圆O的直径,C、D是半圆O上的两点,且OD∥BC,OD与AC交于点E.
(1)若∠B=70°,求∠CAD的度数;
(2)若AB=4,AC=3,求DE的长.
18.如图,⊙O的内接四边形ABCD两组对边的延长线分别交于点E,F.
(1)若∠E+∠F=α,求∠A的度数(用含α的式子表示);
(2)若∠E+∠F=60°,求∠A的度数.
19.如图,⊙O中,直径CD⊥弦AB于E,AM⊥BC于M,交CD于N,连AD.
(1)求证:AD=AN;
(2)若AE=,ON=1,求⊙O的半径.
20.如图,A,P,B,C是⊙O上的四个点,∠APC=∠CPB=60°
(1)判断△ABC的形状,并证明你的结论;
(2)若BC的长为6,求⊙O的半径.
21.如图,四边形ABCD是⊙O的内接四边形,点F是CD延长线上的一点,且AD平分∠BDF,AE⊥CD于点E.
(1)求证:AB=AC.
(2)若BD=11,DE=2,求CD的长.
参考答案
一.选择题(共8小题,满分40分)
1.解:如图,在⊙O中,有弦AB、弦DB、弦CB、弦CD.共有4条弦.
故选:C.
2.解:作直径CF,连接BF,如图,
则∠FBC=90°,
∵∠BAC+∠EAD=180°,
而∠BAC+∠BAF=180°,
∴∠DAE=∠BAF,
∴=,
∴DE=BF=6,
∴BC==8.
解法二:如图,过点A作AM⊥BC于M,AN⊥DE于N.
∵AM⊥BC,AN⊥DE,
∴CM=MB,DN=NE=3,
∵AC=AB=AD=AE,
∴∠BAC=2∠MAC,∠EAD=2∠DAN,
∵∠BAC+∠EAD=180°,
∴2∠CAM+2∠DAN=180°,
∴∠CAM+∠DAN=90°,
∵∠ACM+∠CAM=90°,
∴∠ACM=∠DAN,
∵∠AMC=∠AND=90°,
∴△AMC≌△DNA(AAS),
∴AM=DN=3,
∴CM===4,
∴BC=2CM=8.
故选:A.
3.解:连接OA,
∵OD⊥AB,
∴AD=AB=4(mm),
由勾股定理得,OA==5(mm),
故选:C.
4.解:①相等的圆心角所对的弧相等;错误.必须在同圆或等圆中;
②平分弦的直径一定垂直于弦;错误,此弦不是直径;
③圆是轴对称图形,每一条直径都是对称轴;错误,应该是每一条直径所在的直线都是对称轴;
④直径是弦;正确;
⑤长度相等的弧是等弧.错误.能够完全重合的两条弧是等弧;
故选:A.
5.解:∵四边形ABCD内接于⊙O,
∴∠D+∠B=180°,
又∠B=α,
∴∠D=180°﹣∠B=180°﹣α.
故选:D.
6.解:∵AP BP=CP DP,
∴PD=,
∵AP=3,BP=4,CP=2,
∴PD=6,
∴CD=PC+PD=2+6=8.
故选:C.
7.解:如图,连接BD,
∴∠CDB=∠CAB=51°,
∵AB是⊙O的直径,
∴∠ADB=90°,
∴∠ADC=90°﹣∠CDB=39°,
故选:D.
8.解:设⊙O的半径为r寸.
在Rt△ADO中,AD=5寸,OD=(r﹣1)寸,OA=r寸,
则有r2=52+(r﹣1)2,
解得r=13,
∴⊙O的直径为26寸,
故选:C.
二.填空题(共6小题,满分30分)
9.解:连接OA,
∵OA=OC=10cm,CD=4cm,
∴OD=10﹣4=6cm,
在Rt△OAD中,有勾股定理得:AD==8cm,
∵OC⊥AB,OC过O,
∴AB=2AD=16cm.
故答案为16.
10.解:EF的中点M,作MN⊥AD于点M,取MN上的球心O,连接OF,
∵四边形ABCD是矩形,
∴∠C=∠D=90°,
∴四边形CDMN是矩形,
∴MN=CD=4,
设OF=x,则ON=OF,
∴OM=MN﹣ON=4﹣x,MF=2,
在直角三角形OMF中,OM2+MF2=OF2
即:(4﹣x)2+22=x2
解得:x=2.5
故答案为:2.5
11.解:连接OA,过点O作OD⊥AB于点D,
∵OA=2,AB=2,
∴AD=BD=2,
∴AD:OA=:2,
∴∠AOD=60°,
∴∠AOB=120°,
∴∠AMB=60°,
∴∠ANB=120°.
故答案为:60°或120°.
12.解:∵圆内接四边形的对角互补,
∴∠A+∠BCD=180°,
∵∠A=60°,
∴∠BCD=120°,
∴∠DCE=180°﹣∠BCD=60°,
故答案为;圆内接四边形的对角互补,60°.
13.解:由AB=OC,得
AB=OB,
∠A=∠AOB.
由BO=EO,得
∠BEO=∠EBO.
由∠EBO是△ABO的外角,得
∠EBO=∠A+∠AOB=2∠A,
∠BEO=∠EBO=2∠A.
由∠DOE是△AOE的外角,得
∠A+∠AEO=∠EOD,
即∠A+2∠A=84°,
∠A=28°.
故答案为:28°.
14.解:如图,连接OC,设OB交CD于K.
∵AB=CD,OD=OC=OB=OA,
∴△AOB≌△COD(SSS),
∴∠CDO=∠OBA,
∵∠DKO=∠BKE,
∴∠DOK=∠BEK=α,
即∠BOD=α,故①正确,
不妨设,∠OAB=90°﹣α,
∵OA=OB,
∴∠OAB=∠OBA,
∴∠OBE+∠BEK=90°,
∴∠BKE=90°,
∴OB⊥CD,从条件上看,AB=CD,推不出OB⊥CD这样的位置关系,故②错误,
∵CD=AB,
∴=,
∴=,
∴∠ABC=∠DOB=α,故③正确.
故答案为①③.
三.解答题(共7小题,满分50分)
15.解:连接OC,
∵AB=5cm,
∴OC=OA=AB=cm,
Rt△CDO中,由勾股定理得:DO==cm,
∴AD=﹣=1cm,
由勾股定理得:AC==,
则AD的长为1cm,AC的长为cm.
16.证明:∵AD=BC,
∴=,
∴+=+,
即=,
∴DC=AB.
17.解:(1)∵AB是半圆O的直径,
∴∠ACB=90°,
又∵OD∥BC,
∴∠AEO=90°,即OE⊥AC,
∠CAB=90°﹣∠B=90°﹣70°=20°,∠AOD=∠B=70°.
∵OA=OD,
∴∠DAO=∠ADO=(180°﹣∠AOD)=(180°﹣70°)=55°,
∴∠CAD=∠DAO﹣∠CAB=55°﹣20°=35°;
(2)在直角△ABC中,BC===.
∵OE⊥AC,
∴AE=EC,
又∵OA=OB,
∴OE=BC=.
又∵OD=AB=2,
∴DE=OD﹣OE=2﹣.
18.解:(1)∵四边形ABCD为⊙O的内接四边形,
∴∠A=∠BCF,
∵∠EBF=∠A+∠E,
而∠EBF=180°﹣∠BCF﹣∠F,
∴∠A+∠E=180°﹣∠BCF﹣∠F,
∴∠A+∠E=180﹣∠A﹣∠F,
即2∠A=180°﹣(∠E+∠F),
∵∠E+∠F=α,
∴∠A=90°﹣α;
(2)当α=60°时,∠A=90°﹣×60°=60°.
19.(1)证明:∵∠BAD与∠BCD是同弧所对的圆周角,
∴∠BAD=∠BCD,
∵AE⊥CD,AM⊥BC,
∴∠AMC=∠AEN=90°,
∵∠ANE=∠CNM,
∴∠BCD=∠BAM,
∴∠BAM=BAD,
在△ANE与△ADE中,
,
∴△ANE≌△ADE,
∴AD=AN;
(2)∵AE=2,AE⊥CD,
又∵ON=1,
∴设NE=x,则OE=x﹣1,NE=ED=x,
r=OD=OE+ED=2x﹣1
连接AO,则AO=OD=2x﹣1,
∵△AOE是直角三角形,AE=2,OE=x﹣1,AO=2x﹣1,
∴(2)2+(x﹣1)2=(2x﹣1)2,
解得x=2,
∴r=2x﹣1=3;
20.解:(1)△ABC是等边三角形,
理由如下:由圆周角定理得,∠ABC=∠APC=60°,∠CAB=∠CPB=60°,
∴△ABC是等边三角形;
(2)延长BO交⊙O于E,连接CE,
由圆周角定理得,∠E=∠BAC=60°,
∴BE=4,
∴⊙O的半径为2.
21.(1)证明:∵AD平分∠BDF,
∴∠ADF=∠ADB,
∵∠ABC+∠ADC=180°,∠ADC+∠ADF=180°,
∴∠ADF=∠ABC,
∵∠ACB=∠ADB,
∴∠ABC=∠ACB,
∴AB=AC;
(2)解:过点A作AG⊥BD,垂足为点G.
∵AD平分∠BDF,AE⊥CF,AG⊥BD,
∴AG=AE,∠AGB=∠AEC=90°,
在Rt△AED和Rt△AGD中,
,
∴Rt△AED≌Rt△AGD,
∴GD=ED=2,
在Rt△AEC和Rt△AGB中,
,
∴Rt△AEC≌Rt△AGB(HL),
∴BG=CE,
∵BD=11,
∴BG=BD﹣GD=11﹣2=9,
∴CE=BG=9,
∴CD=CE﹣DE=9﹣2=7.
同课章节目录
