5.2 函数的表示方法 同步练习(Word版含答案)
文档属性
| 名称 | 5.2 函数的表示方法 同步练习(Word版含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 219.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-18 21:06:36 | ||
图片预览





文档简介
《第二节 函数的表示方法》同步练习
一、基础巩固
知识点1 函数的表示方法
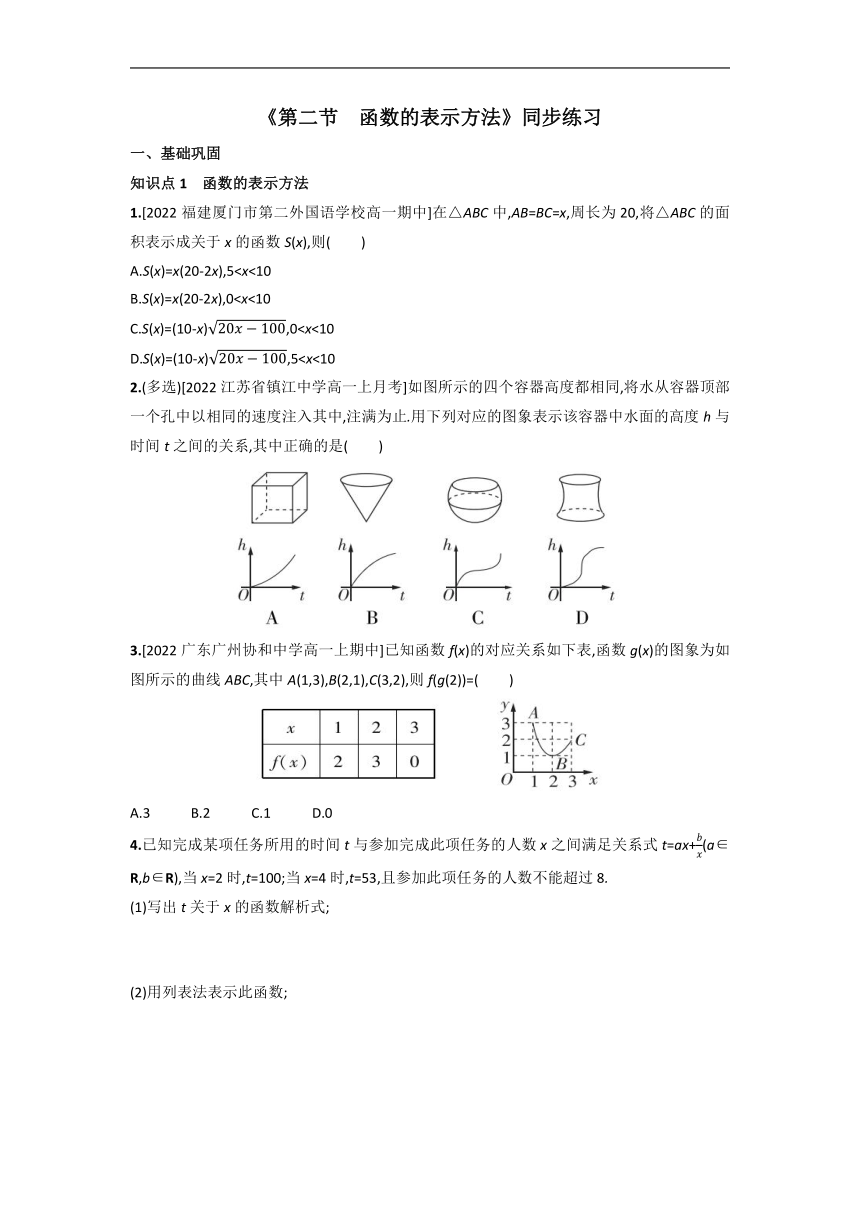
1.[2022福建厦门市第二外国语学校高一期中]在△ABC中,AB=BC=x,周长为20,将△ABC的面积表示成关于x的函数S(x),则( )
A.S(x)=x(20-2x),5B.S(x)=x(20-2x),0C.S(x)=(10-x),0D.S(x)=(10-x),52.(多选)[2022江苏省镇江中学高一上月考]如图所示的四个容器高度都相同,将水从容器顶部一个孔中以相同的速度注入其中,注满为止.用下列对应的图象表示该容器中水面的高度h与时间t之间的关系,其中正确的是( )
3.[2022广东广州协和中学高一上期中]已知函数f(x)的对应关系如下表,函数g(x)的图象为如图所示的曲线ABC,其中A(1,3),B(2,1),C(3,2),则f(g(2))=( )
A.3 B.2 C.1 D.0
4.已知完成某项任务所用的时间t与参加完成此项任务的人数x之间满足关系式t=ax+(a∈R,b∈R),当x=2时,t=100;当x=4时,t=53,且参加此项任务的人数不能超过8.
(1)写出t关于x的函数解析式;
(2)用列表法表示此函数;
(3)画出此函数的图象.
知识点2 函数的解析式的求解
5.[2022江苏南京外国语学校高一期中]若函数f(2x+1)=6x+4,则f(x)=( )
A.3x+1 B.3x-1 C.6x+1 D.6x+3
6.(多选)[2022江苏省盐城中学高一期中]一次函数f(x)满足f(f(x))=4x+3,则f(x)可以是( )
A.2x+1 B.1-2x C.2x-3 D.-2x-3
7.[2021安徽蚌埠怀远一中高一上月考]已知集合A={-1,0,1},B={0,1,2},试写出从A到B的一个函数h(x)= .
8.(1)已知f(x)=x2,求f(2x+1)的解析式;
(2)已知f(+2)=x+4,求函数f(x)的解析式;
(3)已知f(x)是二次函数,且满足f(0)=1,f(x+1)=f(x)+2x,求函数f(x)的解析式;
(4)已知f(x)+2f(-x)=2x+3,求f(x)的解析式.
知识点3 分段函数
9.已知f(x)=则f(f(2))=( )
A.5 B.-1 C.-7 D.2
10.(多选)[2022广东广州执信中学高一期中]设函数f(x)=若f(a)=4,则实数a的值可以是( )
A.2 B.-2 C.4 D.-4
11.[2022江苏启东市汇龙中学高一期中]定义运算ab=设函数f(x)=x(x+1),则该函数的图象是( )
12.[2022甘肃平凉静宁一中高三月考]已知函数f(x)=则函数f(x)的值域为( )
A.R B.(-∞,1]∪[2,+∞)
C.[1,2] D.(-∞,-1]∪[2,+∞)
13.[2022湖北武汉部分学校高一上期末]国家规定个人稿酬纳税办法:不超过800元的不纳税;超过800元而不超过4 000元的按超过800元部分的14%纳税;超过4 000元的按全部稿酬的11.2%纳税.已知某人出版一本书,共纳税420元,则这个人应得稿酬(扣税前)为( )
A.2 800元 B.3 000元
C.3 800元 D.3 818元
14.作出下列函数的图象:
(1) f(x)=|x-1|+|x+1|.
(2)f(x)=
15.[2022江苏盐城阜宁县高一上期中]已知函数y=|x|(x-4).
(1)将函数y=|x|(x-4)写成分段函数的形式,并画出图象.
(2)利用图象回答:当k为何值时,关于x的方程|x|(x-4)=k有一个解 有两个解 有三个解
16.如图所示,已知底角为45°的等腰梯形ABCD,底边BC长为7 cm,腰长为2 cm,当垂直于底边BC(垂足为F)的直线l从左至右移动(与梯形ABCD有公共点)时,直线l把梯形分成两部分,令BF=x,试写出直线l左边部分的面积y关于x的函数解析式,并画出大致图象.
二、能力提升
1.定义:[x]表示不超过实数x的最大整数,称为“地板函数”.年级要召开学生代表大会,规定各班每10人推选一名代表,当各班人数除以10的余数大于5时可增选一名代表,那么各班可推选代表人数y与该班人数x之间的函数关系用“地板函数”可以表示为( )
A.y=[] B.y=[]
C.y=[] D.y=[]
2.(多选)[2022辽宁葫芦岛协作校高一上联考]若函数f(1-2x)=(x≠0),则( )
A.f()=15
B.f(2)=-
C.f(x)=-1(x≠0)
D.f()=-1(x≠0且x≠1)
3.[2022江苏泰州高一上期末]若函数f(x)和g(x)分别由下表给出,则不等式f(g(x))≥0的解集为( )
A.{2} B.{3}
C.{1,3} D.{1,2}
4.(多选)[2022四川成都七中高一上期中]设函数y=f(x)的定义域为R,对于任意给定的正数p,定义函数fp(x)= 则称函数fp(x)为f(x)的“p界函数”.若给定函数f(x)=x2-2x-1,p=2,则下列结论不成立的是( )
A.fp(f(0))=f(fp(0))
B.fp(f(1))=f(fp(1))
C.fp(fp(2))=f(f(2))
D.fp(fp(3))=f(f(3))
5.[2022江苏苏南三校高三下调研]在一种新型流行病疫情防控中,病毒检测是确诊患病与否的有效快捷手段.某医院在成为病毒检测的定点医院并开展检测工作的第n天,每个检测对象平均耗时t(n)(单位:h)大致服从的关系为t(n)=
t0,N0为常数.已知第16天每个检测对象平均耗时为16 h,第64天和第67天每个检测对象平均耗时均为8 h,
则第25天每个检测对象平均耗时大致为( )
A.16 h B.13 h C.9 h D.8 h
6.[2022江苏南京外国语学校高一上期中]已知函数f(x)满足 x,y∈R,f(xy)=f(x)f(y),写出一个符合要求的解析式f(x)= .
7.[2022江苏省金湖中学、涟水中学等七校高一上期中联考]已知函数f(x)=则f(f(4))= ;若存在实数a,使得f(a)=f(f(a)),则实数a的个数是 .
8.已知函数f(x)=
(1)若有且仅有三个不相等的正数x1,x2,x3,使得f(x1)=f(x2)=f(x3),则x1+x2+x3的值为 ;
(2)若存在09.某省两城市之间人员交流频繁,为了缓解交通压力,特修一条专用铁路,用一列火车作为交通车,若该车车头每次拖4节车厢,每天能来回16次(来、回各算作一次),若每次拖7节车厢,则每天能来回10次.
(1)若每天来回的次数是车头每次拖挂车厢节数的一次函数,求此一次函数的解析式.
(2)在(1)的条件下,每节车厢能载客110人.问这列火车每天来回多少次才能使载客人数最多 并求出每天最多载客人数.
10.如图所示的自动通风设施.该设施的下部分ABCD是等腰梯形,其中AB为2 m,梯形的高为1 m,CD为3 m,上部分是以CD为直径的半圆,固定点E为CD的中点.MN是由电脑控制可以上下滑动的伸缩横杆(横杆的截面积可忽略不计),且滑动过程中始终和CD保持平行.当MN位于CD下方(图1)和上方(图2)时,通风窗的形状均为矩形MNGH(阴影部分均不通风).设MN与AB之间的距离为x(0≤x<且x≠1)m,试将通风窗的通风面积S(单位:m2)表示成关于x的函数S(x).
11.设函数y=f(x)的定义域与函数y=f(f(x))的定义域的交集为D,若对任意的x∈D,都有f(f(x))=x,则称函数f(x)是集合M的元素.
(1)判断函数f(x)=2x-1和g(x)=是不是集合M中的元素,并说明理由;
(2)设函数f(x)∈M,且f(x)=kx+b(k,b为常数,且k≠0),试求函数f(x)的解析式;
(3)已知a≠0,f(x)=∈M,试求实数a,b应满足的关系.
12.[2022江苏南京二十九中高一上期中]在①f(a)=5,②f()=a,③2f(1)=f(2)+1这三个条件中任选一个,补充到下面的横线上,并作答.
已知一次函数f(x)满足f(x+1)=ax+3,且 (其中a∈R).
(1)求f(x)的函数解析式;
(2)解关于x的不等式xf(x)≤2b2+b(b∈R).
参考答案
一、基础巩固
1.D 由题意知△ABC是等腰三角形,则S(x)=(20-2x)=(10-x),又解得52.BCD
3.B 观察函数g(x)的图象得g(2)=1,由表格知f(1)=2,所以f(g(2))=f(1)=2.
4.(1)由题意,可得解得所以t=x+.
又x≤8,x为正整数,
所以此函数的定义域是{x|0故此函数的解析式是t=x+(0(2)由(1)知x=1,2,3,4,5,6,7,8,
x,t的值列表如下:
x 1 2 3 4 5 6 7 8
t 197 100 53 35
(3)此函数的图象如图所示:
5.A 令t=2x+1,则x=t-,所以f(t)=6(t-)+4=3t+1,所以f(x)=3x+1.
6.AD 设f(x)=ax+b(a≠0),所以f(f(x))=af(x)+b=a(ax+b)+b=a2x+ab+b=4x+3,所以解得或所以f(x)=2x+1或f(x)=-2x-3.
7.x+1(答案不唯一)
8.(1)因为f(x)=x2,
所以f(2x+1)=(2x+1)2=4x2+4x+1.
(2)方法一 设t=+2,
则t≥2,=t-2,即x=(t-2)2,
所以f(t)=(t-2)2+4(t-2)=t2-4,
所以f(x)=x2-4(x≥2).
方法二 因为f(+2)=(+2)2-4,
所以f(x)=x2-4(x≥2).
(3)因为f(x)是二次函数,
所以设f(x)=ax2+bx+c(a≠0).
由f(0)=1,得c=1.
由f(x+1)=f(x)+2x,得a(x+1)2+b(x+1)+1=ax2+bx+1+2x,整理得(2a-2)x+(a+b)=0,
所以所以
所以f(x)=x2-x+1.
(4)用-x替换f(x)+2f(-x)=2x+3中的x,
得f(-x)+2f(x)=-2x+3.
由
解得f(x)=-2x+1.
9. D 因为f(x)=所以f(2)=-2×2+3=-1,所以f(f(2))=f(-1)=(-1)2+1=2.故选D.
10.AD 因为f(a)=4,所以或解得a=-4或a=2.故选AD.
11.C 由ab的定义可知f(x)=因为f(0)=0-1=-1,所以函数图象过点(0,-1),排除A,B;当x<0时,f(x)=x2>0,排除D,只有C符合.
12.B 当x≤0时,f(x)=-x2-2x=-(x+1)2+1,因为当x=-1时,f(x)取得最大值1,所以x≤0时,函数f(x)的取值范围为(-∞,1].当x>0时, f(x)==x+-2,由基本不等式可得x+≥2=4(当且仅当x=,即x=2时等号成立),所以x>0时,函数f(x)的取值范围为[2,+∞).综上,函数f(x)的值域为(-∞,1]∪[2,+∞).
13.C
14.(1)因为函数f(x)=,
画出其图象如图①所示.
(2)函数的图象是两段抛物线(部分)与一点,画出其图象如图②所示.
15.(1)当x<0时,y=|x|(x-4)=-x(x-4);
当x≥0时,y=|x|(x-4)=x(x-4).
综上,y=
其函数图象如图所示.
(2)由(1)中函数图象可得当k<-4或k>0时,原方程有一个解;当k=-4或k=0时,原方程有两个解;当-416.如图,过点A,D分别作AG⊥BC,DH⊥BC,垂足分别是G,H.因为四边形ABCD是等腰梯形,
底角为45°,AB=2 cm,
所以BG=AG=DH=HC=2 cm.
又BC=7 cm,所以AD=GH=3 cm.
当点F在BG(不包括点B)上时,即x∈(0,2]时,y=x2;
当点F在GH(不包括点G)上时,即x∈(2,5]时,y=2+2(x-2)=2x-2;
当点F在HC(不包括点H,C)上时,即x∈(5,7)时,y=×(7+3)×2-(7-x)2=-(x-7)2+10.
综上,得直线l左边部分的面积y关于x的函数解析式为y=
其大致图象如图所示.
二、能力提升
1.C
2.AD 令1-2x=t(t≠1),则x=,所以f(t)=-1,则f(x)=-1(x≠1),故C错误;f()=15,故A正确;f(2)=3,故B错误;f()=-1=-1(x≠0且x≠1),故D正确.故选AD.
3.C 当x=1时,f(g(1))=f(0)=0;当x=2时,f(g(2))=f(1)=-1<0;当x=3时,f(g(3))=f(-1)=1>0.综上,不等式f(g(x))≥0的解集为{1,3}.
4.ACD 5.B
6.x
7.1 5
8.(1)12;(2)(96,100)
9.(1)设每天来回y次,每次拖挂x(x∈N*)节车厢,则可设y=kx+b(k≠0).
由题意,得16=4k+b,10=7k+b,解得k=-2,b=24,所以y=-2x+24(x∈N*).
(2)设S为每天营运的车厢数,则S=x(-2x+24)=-2x2+24x=-2(x-6)2+72,
所以当x=6时,Smax=72,此时y=12,
则这列火车每天最多载客人数为110×72=7 920.
所以这列火车每天来回12次,才能使载客人数最多,每天最多载客人数为7 920.
10.当0≤x<1时,过点A作AK⊥CD于点K,则AK=1,DK=,HM=1-x,由=2,得DH=,
所以HG=3-2DH=2+x,
所以S(x)=HM·HG=(1-x)(2+x)=-x2-x+2.
当1则ET=x-1,TN=,
所以MN=2,
所以S(x)=MN·ET=2·(x-1)=(x-1).
综上,S(x)=
11.(1)因为对任意的x∈R,f(f(x))=2(2x-1)-1=4x-3,所以f(x)=2x-1 M.
因为对任意的x∈(-∞,0)∪(0,+∞),
g(g(x))==x,所以g(x)∈M.
故f(x)不是集合M的元素,g(x)是集合M的元素.
(2)因为函数f(x)∈M,且f(x)=kx+b(k≠0),所以f(f(x))=k(kx+b)+b=x,
所以解得或
所以f(x)=x或f(x)=-x+b(b∈R).
(3)易知y=f(x)与y=f(f(x))的定义域的交集D由满足的x构成.
因为f(x)=∈M,所以f(f(x))=x对x∈D恒成立,所以=x,即(a+b)x2-(a2-b2)x=0对x∈D恒成立,故a+b=0.
12.方案一 选择条件①.
(1)设f(x)=kx+b(k≠0),则f(x+1)=k(x+1)+b=kx+k+b.
又f(x+1)=ax+3,且f(a)=5,
所以解得或
所以f(x)=-x+4或f(x)=2x+1.
(2)当f(x)=2x+1时,xf(x)=2x2+x,
所以2x2+x≤2b2+b,即2x2+x-b(2b+1)≤0,
即[2x+(2b+1)](x-b)≤0.
当-=b,即b=-时,解得x=-;
当->b,即b<-时,解得b≤x≤-;
当--时,解得-≤x≤b.
综上,当b=-时,原不等式的解集为{-};
当b<-时,原不等式的解集为[b,-];
当b>-时,原不等式的解集为[-,b].
当f(x)=-x+4时,xf(x)=-x2+4x,
所以-x2+4x≤2b2+b,即x2-4x+2b2+b≥0.
当Δ=(-4)2-4(2b2+b)≤0,即b≤或b≥时,不等式的解集为R;
当Δ=(-4)2-4(2b2+b)>0,即综上,当b≤或b≥时,不等式的解集为R;当方案二 选择条件②.
(1)设f(x)=kx+b(k≠0),则f(x+1)=k(x+1)+b=kx+k+b.
又f(x+1)=ax+3,且f()=a,
所以解得所以f(x)=2x+1.
(2)由(1)知f(x)=2x+1,则xf(x)=2x2+x,
所以2x2+x≤2b2+b,即2x2+x-b(2b+1)≤0,
即[2x+(2b+1)](x-b)≤0.
当-=b,即b=-时,解得x=-;
当->b,即b<-时,解得b≤x≤-;
当--时,解得-≤x≤b.
综上,当b=-时,原不等式的解集为{-};
当b<-时,原不等式的解集为[b,-];
当b>-时,原不等式的解集为[-,b].
方案三 选择条件③.
(1)设f(x)=kx+b(k≠0),则f(x+1)=k(x+1)+b=kx+k+b.
又f(x+1)=ax+3,且2f(1)=f(2)+1,
则解得
所以f(x)=2x+1.
(2)同方案二.
一、基础巩固
知识点1 函数的表示方法
1.[2022福建厦门市第二外国语学校高一期中]在△ABC中,AB=BC=x,周长为20,将△ABC的面积表示成关于x的函数S(x),则( )
A.S(x)=x(20-2x),5
3.[2022广东广州协和中学高一上期中]已知函数f(x)的对应关系如下表,函数g(x)的图象为如图所示的曲线ABC,其中A(1,3),B(2,1),C(3,2),则f(g(2))=( )
A.3 B.2 C.1 D.0
4.已知完成某项任务所用的时间t与参加完成此项任务的人数x之间满足关系式t=ax+(a∈R,b∈R),当x=2时,t=100;当x=4时,t=53,且参加此项任务的人数不能超过8.
(1)写出t关于x的函数解析式;
(2)用列表法表示此函数;
(3)画出此函数的图象.
知识点2 函数的解析式的求解
5.[2022江苏南京外国语学校高一期中]若函数f(2x+1)=6x+4,则f(x)=( )
A.3x+1 B.3x-1 C.6x+1 D.6x+3
6.(多选)[2022江苏省盐城中学高一期中]一次函数f(x)满足f(f(x))=4x+3,则f(x)可以是( )
A.2x+1 B.1-2x C.2x-3 D.-2x-3
7.[2021安徽蚌埠怀远一中高一上月考]已知集合A={-1,0,1},B={0,1,2},试写出从A到B的一个函数h(x)= .
8.(1)已知f(x)=x2,求f(2x+1)的解析式;
(2)已知f(+2)=x+4,求函数f(x)的解析式;
(3)已知f(x)是二次函数,且满足f(0)=1,f(x+1)=f(x)+2x,求函数f(x)的解析式;
(4)已知f(x)+2f(-x)=2x+3,求f(x)的解析式.
知识点3 分段函数
9.已知f(x)=则f(f(2))=( )
A.5 B.-1 C.-7 D.2
10.(多选)[2022广东广州执信中学高一期中]设函数f(x)=若f(a)=4,则实数a的值可以是( )
A.2 B.-2 C.4 D.-4
11.[2022江苏启东市汇龙中学高一期中]定义运算ab=设函数f(x)=x(x+1),则该函数的图象是( )
12.[2022甘肃平凉静宁一中高三月考]已知函数f(x)=则函数f(x)的值域为( )
A.R B.(-∞,1]∪[2,+∞)
C.[1,2] D.(-∞,-1]∪[2,+∞)
13.[2022湖北武汉部分学校高一上期末]国家规定个人稿酬纳税办法:不超过800元的不纳税;超过800元而不超过4 000元的按超过800元部分的14%纳税;超过4 000元的按全部稿酬的11.2%纳税.已知某人出版一本书,共纳税420元,则这个人应得稿酬(扣税前)为( )
A.2 800元 B.3 000元
C.3 800元 D.3 818元
14.作出下列函数的图象:
(1) f(x)=|x-1|+|x+1|.
(2)f(x)=
15.[2022江苏盐城阜宁县高一上期中]已知函数y=|x|(x-4).
(1)将函数y=|x|(x-4)写成分段函数的形式,并画出图象.
(2)利用图象回答:当k为何值时,关于x的方程|x|(x-4)=k有一个解 有两个解 有三个解
16.如图所示,已知底角为45°的等腰梯形ABCD,底边BC长为7 cm,腰长为2 cm,当垂直于底边BC(垂足为F)的直线l从左至右移动(与梯形ABCD有公共点)时,直线l把梯形分成两部分,令BF=x,试写出直线l左边部分的面积y关于x的函数解析式,并画出大致图象.
二、能力提升
1.定义:[x]表示不超过实数x的最大整数,称为“地板函数”.年级要召开学生代表大会,规定各班每10人推选一名代表,当各班人数除以10的余数大于5时可增选一名代表,那么各班可推选代表人数y与该班人数x之间的函数关系用“地板函数”可以表示为( )
A.y=[] B.y=[]
C.y=[] D.y=[]
2.(多选)[2022辽宁葫芦岛协作校高一上联考]若函数f(1-2x)=(x≠0),则( )
A.f()=15
B.f(2)=-
C.f(x)=-1(x≠0)
D.f()=-1(x≠0且x≠1)
3.[2022江苏泰州高一上期末]若函数f(x)和g(x)分别由下表给出,则不等式f(g(x))≥0的解集为( )
A.{2} B.{3}
C.{1,3} D.{1,2}
4.(多选)[2022四川成都七中高一上期中]设函数y=f(x)的定义域为R,对于任意给定的正数p,定义函数fp(x)= 则称函数fp(x)为f(x)的“p界函数”.若给定函数f(x)=x2-2x-1,p=2,则下列结论不成立的是( )
A.fp(f(0))=f(fp(0))
B.fp(f(1))=f(fp(1))
C.fp(fp(2))=f(f(2))
D.fp(fp(3))=f(f(3))
5.[2022江苏苏南三校高三下调研]在一种新型流行病疫情防控中,病毒检测是确诊患病与否的有效快捷手段.某医院在成为病毒检测的定点医院并开展检测工作的第n天,每个检测对象平均耗时t(n)(单位:h)大致服从的关系为t(n)=
t0,N0为常数.已知第16天每个检测对象平均耗时为16 h,第64天和第67天每个检测对象平均耗时均为8 h,
则第25天每个检测对象平均耗时大致为( )
A.16 h B.13 h C.9 h D.8 h
6.[2022江苏南京外国语学校高一上期中]已知函数f(x)满足 x,y∈R,f(xy)=f(x)f(y),写出一个符合要求的解析式f(x)= .
7.[2022江苏省金湖中学、涟水中学等七校高一上期中联考]已知函数f(x)=则f(f(4))= ;若存在实数a,使得f(a)=f(f(a)),则实数a的个数是 .
8.已知函数f(x)=
(1)若有且仅有三个不相等的正数x1,x2,x3,使得f(x1)=f(x2)=f(x3),则x1+x2+x3的值为 ;
(2)若存在0
(1)若每天来回的次数是车头每次拖挂车厢节数的一次函数,求此一次函数的解析式.
(2)在(1)的条件下,每节车厢能载客110人.问这列火车每天来回多少次才能使载客人数最多 并求出每天最多载客人数.
10.如图所示的自动通风设施.该设施的下部分ABCD是等腰梯形,其中AB为2 m,梯形的高为1 m,CD为3 m,上部分是以CD为直径的半圆,固定点E为CD的中点.MN是由电脑控制可以上下滑动的伸缩横杆(横杆的截面积可忽略不计),且滑动过程中始终和CD保持平行.当MN位于CD下方(图1)和上方(图2)时,通风窗的形状均为矩形MNGH(阴影部分均不通风).设MN与AB之间的距离为x(0≤x<且x≠1)m,试将通风窗的通风面积S(单位:m2)表示成关于x的函数S(x).
11.设函数y=f(x)的定义域与函数y=f(f(x))的定义域的交集为D,若对任意的x∈D,都有f(f(x))=x,则称函数f(x)是集合M的元素.
(1)判断函数f(x)=2x-1和g(x)=是不是集合M中的元素,并说明理由;
(2)设函数f(x)∈M,且f(x)=kx+b(k,b为常数,且k≠0),试求函数f(x)的解析式;
(3)已知a≠0,f(x)=∈M,试求实数a,b应满足的关系.
12.[2022江苏南京二十九中高一上期中]在①f(a)=5,②f()=a,③2f(1)=f(2)+1这三个条件中任选一个,补充到下面的横线上,并作答.
已知一次函数f(x)满足f(x+1)=ax+3,且 (其中a∈R).
(1)求f(x)的函数解析式;
(2)解关于x的不等式xf(x)≤2b2+b(b∈R).
参考答案
一、基础巩固
1.D 由题意知△ABC是等腰三角形,则S(x)=(20-2x)=(10-x),又解得5
3.B 观察函数g(x)的图象得g(2)=1,由表格知f(1)=2,所以f(g(2))=f(1)=2.
4.(1)由题意,可得解得所以t=x+.
又x≤8,x为正整数,
所以此函数的定义域是{x|0
x,t的值列表如下:
x 1 2 3 4 5 6 7 8
t 197 100 53 35
(3)此函数的图象如图所示:
5.A 令t=2x+1,则x=t-,所以f(t)=6(t-)+4=3t+1,所以f(x)=3x+1.
6.AD 设f(x)=ax+b(a≠0),所以f(f(x))=af(x)+b=a(ax+b)+b=a2x+ab+b=4x+3,所以解得或所以f(x)=2x+1或f(x)=-2x-3.
7.x+1(答案不唯一)
8.(1)因为f(x)=x2,
所以f(2x+1)=(2x+1)2=4x2+4x+1.
(2)方法一 设t=+2,
则t≥2,=t-2,即x=(t-2)2,
所以f(t)=(t-2)2+4(t-2)=t2-4,
所以f(x)=x2-4(x≥2).
方法二 因为f(+2)=(+2)2-4,
所以f(x)=x2-4(x≥2).
(3)因为f(x)是二次函数,
所以设f(x)=ax2+bx+c(a≠0).
由f(0)=1,得c=1.
由f(x+1)=f(x)+2x,得a(x+1)2+b(x+1)+1=ax2+bx+1+2x,整理得(2a-2)x+(a+b)=0,
所以所以
所以f(x)=x2-x+1.
(4)用-x替换f(x)+2f(-x)=2x+3中的x,
得f(-x)+2f(x)=-2x+3.
由
解得f(x)=-2x+1.
9. D 因为f(x)=所以f(2)=-2×2+3=-1,所以f(f(2))=f(-1)=(-1)2+1=2.故选D.
10.AD 因为f(a)=4,所以或解得a=-4或a=2.故选AD.
11.C 由ab的定义可知f(x)=因为f(0)=0-1=-1,所以函数图象过点(0,-1),排除A,B;当x<0时,f(x)=x2>0,排除D,只有C符合.
12.B 当x≤0时,f(x)=-x2-2x=-(x+1)2+1,因为当x=-1时,f(x)取得最大值1,所以x≤0时,函数f(x)的取值范围为(-∞,1].当x>0时, f(x)==x+-2,由基本不等式可得x+≥2=4(当且仅当x=,即x=2时等号成立),所以x>0时,函数f(x)的取值范围为[2,+∞).综上,函数f(x)的值域为(-∞,1]∪[2,+∞).
13.C
14.(1)因为函数f(x)=,
画出其图象如图①所示.
(2)函数的图象是两段抛物线(部分)与一点,画出其图象如图②所示.
15.(1)当x<0时,y=|x|(x-4)=-x(x-4);
当x≥0时,y=|x|(x-4)=x(x-4).
综上,y=
其函数图象如图所示.
(2)由(1)中函数图象可得当k<-4或k>0时,原方程有一个解;当k=-4或k=0时,原方程有两个解;当-4
底角为45°,AB=2 cm,
所以BG=AG=DH=HC=2 cm.
又BC=7 cm,所以AD=GH=3 cm.
当点F在BG(不包括点B)上时,即x∈(0,2]时,y=x2;
当点F在GH(不包括点G)上时,即x∈(2,5]时,y=2+2(x-2)=2x-2;
当点F在HC(不包括点H,C)上时,即x∈(5,7)时,y=×(7+3)×2-(7-x)2=-(x-7)2+10.
综上,得直线l左边部分的面积y关于x的函数解析式为y=
其大致图象如图所示.
二、能力提升
1.C
2.AD 令1-2x=t(t≠1),则x=,所以f(t)=-1,则f(x)=-1(x≠1),故C错误;f()=15,故A正确;f(2)=3,故B错误;f()=-1=-1(x≠0且x≠1),故D正确.故选AD.
3.C 当x=1时,f(g(1))=f(0)=0;当x=2时,f(g(2))=f(1)=-1<0;当x=3时,f(g(3))=f(-1)=1>0.综上,不等式f(g(x))≥0的解集为{1,3}.
4.ACD 5.B
6.x
7.1 5
8.(1)12;(2)(96,100)
9.(1)设每天来回y次,每次拖挂x(x∈N*)节车厢,则可设y=kx+b(k≠0).
由题意,得16=4k+b,10=7k+b,解得k=-2,b=24,所以y=-2x+24(x∈N*).
(2)设S为每天营运的车厢数,则S=x(-2x+24)=-2x2+24x=-2(x-6)2+72,
所以当x=6时,Smax=72,此时y=12,
则这列火车每天最多载客人数为110×72=7 920.
所以这列火车每天来回12次,才能使载客人数最多,每天最多载客人数为7 920.
10.当0≤x<1时,过点A作AK⊥CD于点K,则AK=1,DK=,HM=1-x,由=2,得DH=,
所以HG=3-2DH=2+x,
所以S(x)=HM·HG=(1-x)(2+x)=-x2-x+2.
当1
所以MN=2,
所以S(x)=MN·ET=2·(x-1)=(x-1).
综上,S(x)=
11.(1)因为对任意的x∈R,f(f(x))=2(2x-1)-1=4x-3,所以f(x)=2x-1 M.
因为对任意的x∈(-∞,0)∪(0,+∞),
g(g(x))==x,所以g(x)∈M.
故f(x)不是集合M的元素,g(x)是集合M的元素.
(2)因为函数f(x)∈M,且f(x)=kx+b(k≠0),所以f(f(x))=k(kx+b)+b=x,
所以解得或
所以f(x)=x或f(x)=-x+b(b∈R).
(3)易知y=f(x)与y=f(f(x))的定义域的交集D由满足的x构成.
因为f(x)=∈M,所以f(f(x))=x对x∈D恒成立,所以=x,即(a+b)x2-(a2-b2)x=0对x∈D恒成立,故a+b=0.
12.方案一 选择条件①.
(1)设f(x)=kx+b(k≠0),则f(x+1)=k(x+1)+b=kx+k+b.
又f(x+1)=ax+3,且f(a)=5,
所以解得或
所以f(x)=-x+4或f(x)=2x+1.
(2)当f(x)=2x+1时,xf(x)=2x2+x,
所以2x2+x≤2b2+b,即2x2+x-b(2b+1)≤0,
即[2x+(2b+1)](x-b)≤0.
当-=b,即b=-时,解得x=-;
当->b,即b<-时,解得b≤x≤-;
当-
综上,当b=-时,原不等式的解集为{-};
当b<-时,原不等式的解集为[b,-];
当b>-时,原不等式的解集为[-,b].
当f(x)=-x+4时,xf(x)=-x2+4x,
所以-x2+4x≤2b2+b,即x2-4x+2b2+b≥0.
当Δ=(-4)2-4(2b2+b)≤0,即b≤或b≥时,不等式的解集为R;
当Δ=(-4)2-4(2b2+b)>0,即
(1)设f(x)=kx+b(k≠0),则f(x+1)=k(x+1)+b=kx+k+b.
又f(x+1)=ax+3,且f()=a,
所以解得所以f(x)=2x+1.
(2)由(1)知f(x)=2x+1,则xf(x)=2x2+x,
所以2x2+x≤2b2+b,即2x2+x-b(2b+1)≤0,
即[2x+(2b+1)](x-b)≤0.
当-=b,即b=-时,解得x=-;
当->b,即b<-时,解得b≤x≤-;
当-
综上,当b=-时,原不等式的解集为{-};
当b<-时,原不等式的解集为[b,-];
当b>-时,原不等式的解集为[-,b].
方案三 选择条件③.
(1)设f(x)=kx+b(k≠0),则f(x+1)=k(x+1)+b=kx+k+b.
又f(x+1)=ax+3,且2f(1)=f(2)+1,
则解得
所以f(x)=2x+1.
(2)同方案二.
同课章节目录
- 第1章 集合
- 1.1 集合的概念与表示
- 1.2 子集、全集、补集
- 1.3 交集、并集
- 第2章 常用逻辑用语
- 2.1 命题、定理、定义
- 2.2 充分条件、必要条件、冲要条件
- 2.3 全称量词命题与存在量词命题
- 第3章 不等式
- 3.1 不等式的基本性质
- 3.2 基本不等式
- 3.3 从函数观点看一元二次方程和一元二次不等式
- 第4章 指数与对数
- 4.1 指数
- 4.2 对数
- 第5章 函数概念与性质
- 5.1 函数的概念和图象
- 5.2 函数的表示方法
- 5.3 函数的单调性
- 5.4 函数的奇偶性
- 第6章 幂函数、指数函数和对数函数
- 6.1 幂函数
- 6.2 指数函数
- 6.3 对数函数
- 第7章 三角函数
- 7.1 角与弧度
- 7.2 三角函数概念
- 7.3 三角函数的图象和性质
- 7.4 三角函数应用
- 第8章 函数应用
- 8.1 二分法与求方程近似解
- 8.2 函数与数学模型
