1.3 交集、并集 教案
文档属性
| 名称 | 1.3 交集、并集 教案 |

|
|
| 格式 | docx | ||
| 文件大小 | 500.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-18 21:15:25 | ||
图片预览




文档简介
1.3交集、并集
教学目标:
(1)理解两个集合的交集、并集的概念,并会求集合的交集与并集,并掌握集合交、并的相关性质;
(2)能用Venn图表示集合的交集、并集运算的结果,体会直观图对理解抽象概念的作用;
(3)掌握集合中的相关数学术语和符号,并能正确的运用符号进行集合的运算.
教学重难点:
重点:集合的交集、并集运算的含义、识记与运用.
难点:掌握交集、并集的求法,并能用Venn图表示集合运算的结果.
课 型:新授课
教学方法:讲练结合
教学过程
一、情景导入
学校有一个小超市,老板第一周进的货有这么几样:圆珠笔、钢笔、铅笔、笔记本、方便面、火腿肠.一周后进的货有:铅笔、方便面、火腿肠、汽水.大家想一想:哪些商品的销路比较好?
由这些对象为元素分别构成了以下三个集合,请学生用Venn图表示这三个集合.
教材引例:用Venn图分别表示下列各组中的三个集合
⑴;
⑵;
⑶A={x|x为高一⑺班语文测验优秀者},B={x|x为高一⑺班数学测验优秀者},C={x|x为高一⑺班语文、数学测验两门都优秀者}.
上述每组集合中,A、B、C之间均具有怎样的关系?
二、新课讲授
1. 交集
定义:(1)文字语言:一般地,给定两个集合A,B由既属于A又属于集合B的所有元素组成的集合,称为A与B的交集,记作,读作“A交B”.
符号语言:A∩B={x|x∈A且x∈B}
图形语言:
性质探究:A∩B与B∩A、A∩B和A、A∩B和B、A∩ 之间的关系.
尝试与发现:用Venn图分别画出A∩B和B∩A,然后观察A∩B和B∩A的关系、A∩B和A的关系及A∩B和B的关系.
结论:①A∩B=B∩A,②A∩A=A,③A∩ = ∩A= ,
④如果,则,反之也成立.
例1.全集,,,则( )
A. B. C. D.
【答案】B
【分析】根据集合的补集和交集的运算公式进行计算即可.
【详解】因为,,,,
所以,
所以.
故选:B
已知全集,集合,.
(1)若,求;.
(2)若,求实数a的取值范围.
【答案】(1),或.
(2).
【分析】(1)根据集合的运算法则计算;
(2)由得,结合包含关系可得参数范围.
(1)时,,,又或,所以或.
(2)由得,若,即,则满足题意,若,则,无解,综上,.
练习1:已知集合,,则( )
A. B. C. D.
【答案】C
【分析】先化简集合B,再利用交集定义去求
【详解】由,解得,则,
所以.
故选:C.
练习2: 图1中的四块区域Ⅰ,Ⅱ,Ⅲ,Ⅳ分别表示下列四个集合:,,,,则图2中的阴影部分表示的集合为( )
A. B. C. D.
【答案】D
【分析】由集合的运算与Venn图表示判断.
【详解】由题意知题图2中的阴影部分为:集合A与集合B的交集去掉属于集合C的部分,即图2中的阴影部分表示的集合为.
故选:D.
并集
定义:(1)文字语言:一般地,给定两个集合A,B,由这两个集合的所有元素组成的集合,称为集合A与B的并集,记作,读作“A并B”
(2)符号语言:
(3)图形语言:
性质探究:A∪B与B∪A、A∪B和A、A∪B和B、A∪ 之间的关系.
尝试与发现:用Venn图分别画出A∪B和B∪A,然后观察A∪B和B∪A的关系、A∪B和A的关系及A∪B和B的关系.
结论:①A∪B=B∪A,②A∪A=A,③A∪ = ∪A=A,
④如果A B,则A∪B=B,反之也成立.
已知集合,集合,则=( )
A. B. C. D.
【答案】D
【分析】根据给定条件,利用并集的定义直接求解作答.
【详解】因集合,集合,所以.
故选:D
已知全集U=R,集合A={x|1≤x≤3},B={x|x=m+1,m∈A}.
(1)求图中阴影部分表示的集合C;
(2)若非空集合D={x|4﹣a<x<a},且D (A∪B),求实数a的取值范围.
【答案】(1){x|1≤x<2} (2)
【分析】(1)根据条件求出集合A,B结合Venn图即可求图中阴影部分表示的集合C;
(2)根据集合关系进行转化求解即可.
(1)因为,.所以B={x|2≤x≤4},根据题意,由图可得:,因为B={x|2≤x≤4},则={x|x>4或x<2},而A={x|1≤x≤3},则;
(2)因为集合A={x|1≤x≤3},B={x|2≤x≤4},所以A∪B={x|1≤x≤4},若非空集合D={x|4﹣a<x<a},且D (A∪B),则有,解得2<a≤3,即实数a的取值范围为
练习3:已知全集U,集合A,B为其子集,若,则( )
A. B. C.A D.B
【答案】C
【分析】根据给定条件,判断集合A,B的关系,再利用并集的定义计算作答.
【详解】全集U,集合A,B为其子集,因,则有,
所以.
故选:C
练习4:已知集合,,则A∪B=( )
A. B. C. D.
【答案】B
【分析】由并集的定义求解即可.
【详解】∵,
∴.
故选:B.
区间
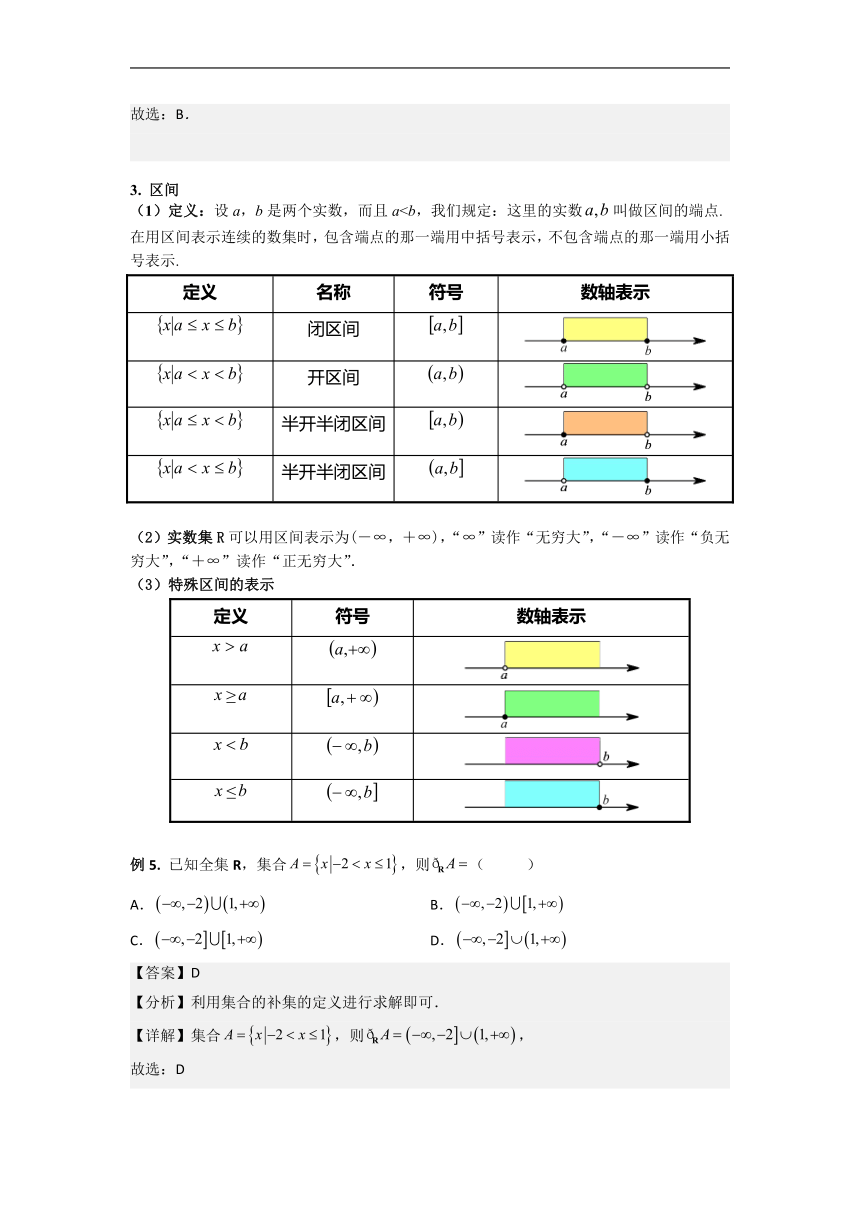
(1)定义:设a,b是两个实数,而且a在用区间表示连续的数集时,包含端点的那一端用中括号表示,不包含端点的那一端用小括号表示.
定义 名称 符号 数轴表示
闭区间
开区间
半开半闭区间
半开半闭区间
(2)实数集R可以用区间表示为(-∞,+∞),“∞”读作“无穷大”,“-∞”读作“负无穷大”,“+∞”读作“正无穷大”.
(3)特殊区间的表示
定义 符号 数轴表示
≥
≤
已知全集R,集合,则( )
A. B.
C. D.
【答案】D
【分析】利用集合的补集的定义进行求解即可.
【详解】集合,则,
故选:D
练习5:已知集合,,则( )
A. B. C. D.
【答案】A
【分析】通过解不等式求出集合、,再求交集.
【详解】由,得,故;
由得,故,
则,所以A正确.
故选:A.
拓展巩固
已知集合,,则( )
A. B. C. D.
【答案】C
【分析】根据两集合的特征结合交集的定义分析求解
【详解】集合A是一个以数为元素的集合,集合B是一个以点为元素的集合,
他们元素的属性不一样,则.
故选:C.
2.设全集,集合,则( )
A. B. C. D.
【答案】A
【分析】先求出,再根据交集的定义可求.
【详解】,故,
故选:A.
3.已知全集,设集合,,则( )
A. B. C. D.
【答案】A
【分析】直接由补集和交集的概念求解即可.
【详解】,所以.
故选:A.
4.已知集合,,则A∪B=( )
A. B. C. D.
【答案】B
【分析】由并集的定义求解即可.
【详解】∵,
∴.
故选:B.
5.设全集,集合 ,,则( )
A. B.
C. D.
【答案】D
【分析】利用集合的补集和并集的定义求解即可.
【详解】因为,所以,
所以,故选:D.
6.已知集合,,则( )
A. B. C. D.
【答案】A
【分析】根据并集的定义,即可求解.
【详解】因为集合,,
所以.
故选:A
7.设全集,集合,则( )
A. B. C. D.
【答案】C
【分析】由并集运算求得,由列举法表示出,再由补集运算求得.
【详解】解:由,,,,得
,,,3,.
又,2,3,4,,
,,
故选:C.
已知全集U,集合A,B为其子集,若,则( )
A. B. C.A D.B
【答案】C
【分析】根据给定条件,判断集合A,B的关系,再利用并集的定义计算作答.
【详解】全集U,集合A,B为其子集,因,则有,
所以.
故选:C
图中阴影部分所表示的集合是( )
A. B.
C. D.
【答案】AC
【分析】根据Venn图,由集合运算的概念,即可得出结果.
【详解】阴影部分所表示的集合中的元素属于N,不属于M,故其表示集合或.
故选:AC.
10.若集合A,B满足:,,则下列关系可能成立的是( )
A.AB B. C.BA D.
【答案】ABD
【分析】根据给定条件,“举例子”说明判断A,B,D;利用子集的定义说明判断C作答.
【详解】当A={1,2},B={1,2,3}时,有,满足条件“,”,且有AB,{1,2},则A正确,B正确.
若BA,则,都有,与“,”矛盾,那么B不可能是A的真子集,则C错误.
当A={1,2},B={3,4}时满足条件“,”且有,则D正确.
故选:ABD
11.设集合,,则下列选项中,满足的实数a的取值范围可以是( )
A.{a|0≤a≤6} B.{a|a≤2或a≥4}
C.{a|a≤0} D.{a|a≥8}
【答案】CD
【分析】由,得到a﹣1≥5或a+1≤1,由此能求出实数a的取值范围.
【详解】∵集合,满足,
∴或,解得或.
∴实数a的取值范围可以是{a|a≤0}或{a|a≥8}.
故选:CD.
集合,.
(1)若,,求实数a的值;
(2)从①,②,③这三个条件中选择一个作为已知条件,求实数a的取值范围.
【答案】(1)1
(2)条件选择见解析,
【分析】(1)由可知、,即可求出答案.
(2)三个条件中选择一个都可得,由此即可列出不等式组,即可求出答案.
(1)
因为,所以,
所以,得或.
当时,,不满足,故舍去;
当时,,满足题意.
故实数a的值为1.
(2)
方案一 选择条件①.
由,得,
所以,解得.
故实数a的取值范围是.
方案二 选择条件②.
由,得,
所以,解得.
故实数a的取值范围是.
方案三 选择条件③.
由,得,
所以解得.
故实数a的取值范围是.
设全集,集合,,
(1)求,
(2)若,求实数的取值范围.
【答案】(1),
(2)
【分析】(1)解一元二次不等式得集合M,按集合的交并补运算即可;
(2)利用集合间的包含关系,列不等式求解.
(1)
解:由得,
所以
由得,
所以
(2)
解:根据集合得,解得
教学目标:
(1)理解两个集合的交集、并集的概念,并会求集合的交集与并集,并掌握集合交、并的相关性质;
(2)能用Venn图表示集合的交集、并集运算的结果,体会直观图对理解抽象概念的作用;
(3)掌握集合中的相关数学术语和符号,并能正确的运用符号进行集合的运算.
教学重难点:
重点:集合的交集、并集运算的含义、识记与运用.
难点:掌握交集、并集的求法,并能用Venn图表示集合运算的结果.
课 型:新授课
教学方法:讲练结合
教学过程
一、情景导入
学校有一个小超市,老板第一周进的货有这么几样:圆珠笔、钢笔、铅笔、笔记本、方便面、火腿肠.一周后进的货有:铅笔、方便面、火腿肠、汽水.大家想一想:哪些商品的销路比较好?
由这些对象为元素分别构成了以下三个集合,请学生用Venn图表示这三个集合.
教材引例:用Venn图分别表示下列各组中的三个集合
⑴;
⑵;
⑶A={x|x为高一⑺班语文测验优秀者},B={x|x为高一⑺班数学测验优秀者},C={x|x为高一⑺班语文、数学测验两门都优秀者}.
上述每组集合中,A、B、C之间均具有怎样的关系?
二、新课讲授
1. 交集
定义:(1)文字语言:一般地,给定两个集合A,B由既属于A又属于集合B的所有元素组成的集合,称为A与B的交集,记作,读作“A交B”.
符号语言:A∩B={x|x∈A且x∈B}
图形语言:
性质探究:A∩B与B∩A、A∩B和A、A∩B和B、A∩ 之间的关系.
尝试与发现:用Venn图分别画出A∩B和B∩A,然后观察A∩B和B∩A的关系、A∩B和A的关系及A∩B和B的关系.
结论:①A∩B=B∩A,②A∩A=A,③A∩ = ∩A= ,
④如果,则,反之也成立.
例1.全集,,,则( )
A. B. C. D.
【答案】B
【分析】根据集合的补集和交集的运算公式进行计算即可.
【详解】因为,,,,
所以,
所以.
故选:B
已知全集,集合,.
(1)若,求;.
(2)若,求实数a的取值范围.
【答案】(1),或.
(2).
【分析】(1)根据集合的运算法则计算;
(2)由得,结合包含关系可得参数范围.
(1)时,,,又或,所以或.
(2)由得,若,即,则满足题意,若,则,无解,综上,.
练习1:已知集合,,则( )
A. B. C. D.
【答案】C
【分析】先化简集合B,再利用交集定义去求
【详解】由,解得,则,
所以.
故选:C.
练习2: 图1中的四块区域Ⅰ,Ⅱ,Ⅲ,Ⅳ分别表示下列四个集合:,,,,则图2中的阴影部分表示的集合为( )
A. B. C. D.
【答案】D
【分析】由集合的运算与Venn图表示判断.
【详解】由题意知题图2中的阴影部分为:集合A与集合B的交集去掉属于集合C的部分,即图2中的阴影部分表示的集合为.
故选:D.
并集
定义:(1)文字语言:一般地,给定两个集合A,B,由这两个集合的所有元素组成的集合,称为集合A与B的并集,记作,读作“A并B”
(2)符号语言:
(3)图形语言:
性质探究:A∪B与B∪A、A∪B和A、A∪B和B、A∪ 之间的关系.
尝试与发现:用Venn图分别画出A∪B和B∪A,然后观察A∪B和B∪A的关系、A∪B和A的关系及A∪B和B的关系.
结论:①A∪B=B∪A,②A∪A=A,③A∪ = ∪A=A,
④如果A B,则A∪B=B,反之也成立.
已知集合,集合,则=( )
A. B. C. D.
【答案】D
【分析】根据给定条件,利用并集的定义直接求解作答.
【详解】因集合,集合,所以.
故选:D
已知全集U=R,集合A={x|1≤x≤3},B={x|x=m+1,m∈A}.
(1)求图中阴影部分表示的集合C;
(2)若非空集合D={x|4﹣a<x<a},且D (A∪B),求实数a的取值范围.
【答案】(1){x|1≤x<2} (2)
【分析】(1)根据条件求出集合A,B结合Venn图即可求图中阴影部分表示的集合C;
(2)根据集合关系进行转化求解即可.
(1)因为,.所以B={x|2≤x≤4},根据题意,由图可得:,因为B={x|2≤x≤4},则={x|x>4或x<2},而A={x|1≤x≤3},则;
(2)因为集合A={x|1≤x≤3},B={x|2≤x≤4},所以A∪B={x|1≤x≤4},若非空集合D={x|4﹣a<x<a},且D (A∪B),则有,解得2<a≤3,即实数a的取值范围为
练习3:已知全集U,集合A,B为其子集,若,则( )
A. B. C.A D.B
【答案】C
【分析】根据给定条件,判断集合A,B的关系,再利用并集的定义计算作答.
【详解】全集U,集合A,B为其子集,因,则有,
所以.
故选:C
练习4:已知集合,,则A∪B=( )
A. B. C. D.
【答案】B
【分析】由并集的定义求解即可.
【详解】∵,
∴.
故选:B.
区间
(1)定义:设a,b是两个实数,而且a
定义 名称 符号 数轴表示
闭区间
开区间
半开半闭区间
半开半闭区间
(2)实数集R可以用区间表示为(-∞,+∞),“∞”读作“无穷大”,“-∞”读作“负无穷大”,“+∞”读作“正无穷大”.
(3)特殊区间的表示
定义 符号 数轴表示
≥
≤
已知全集R,集合,则( )
A. B.
C. D.
【答案】D
【分析】利用集合的补集的定义进行求解即可.
【详解】集合,则,
故选:D
练习5:已知集合,,则( )
A. B. C. D.
【答案】A
【分析】通过解不等式求出集合、,再求交集.
【详解】由,得,故;
由得,故,
则,所以A正确.
故选:A.
拓展巩固
已知集合,,则( )
A. B. C. D.
【答案】C
【分析】根据两集合的特征结合交集的定义分析求解
【详解】集合A是一个以数为元素的集合,集合B是一个以点为元素的集合,
他们元素的属性不一样,则.
故选:C.
2.设全集,集合,则( )
A. B. C. D.
【答案】A
【分析】先求出,再根据交集的定义可求.
【详解】,故,
故选:A.
3.已知全集,设集合,,则( )
A. B. C. D.
【答案】A
【分析】直接由补集和交集的概念求解即可.
【详解】,所以.
故选:A.
4.已知集合,,则A∪B=( )
A. B. C. D.
【答案】B
【分析】由并集的定义求解即可.
【详解】∵,
∴.
故选:B.
5.设全集,集合 ,,则( )
A. B.
C. D.
【答案】D
【分析】利用集合的补集和并集的定义求解即可.
【详解】因为,所以,
所以,故选:D.
6.已知集合,,则( )
A. B. C. D.
【答案】A
【分析】根据并集的定义,即可求解.
【详解】因为集合,,
所以.
故选:A
7.设全集,集合,则( )
A. B. C. D.
【答案】C
【分析】由并集运算求得,由列举法表示出,再由补集运算求得.
【详解】解:由,,,,得
,,,3,.
又,2,3,4,,
,,
故选:C.
已知全集U,集合A,B为其子集,若,则( )
A. B. C.A D.B
【答案】C
【分析】根据给定条件,判断集合A,B的关系,再利用并集的定义计算作答.
【详解】全集U,集合A,B为其子集,因,则有,
所以.
故选:C
图中阴影部分所表示的集合是( )
A. B.
C. D.
【答案】AC
【分析】根据Venn图,由集合运算的概念,即可得出结果.
【详解】阴影部分所表示的集合中的元素属于N,不属于M,故其表示集合或.
故选:AC.
10.若集合A,B满足:,,则下列关系可能成立的是( )
A.AB B. C.BA D.
【答案】ABD
【分析】根据给定条件,“举例子”说明判断A,B,D;利用子集的定义说明判断C作答.
【详解】当A={1,2},B={1,2,3}时,有,满足条件“,”,且有AB,{1,2},则A正确,B正确.
若BA,则,都有,与“,”矛盾,那么B不可能是A的真子集,则C错误.
当A={1,2},B={3,4}时满足条件“,”且有,则D正确.
故选:ABD
11.设集合,,则下列选项中,满足的实数a的取值范围可以是( )
A.{a|0≤a≤6} B.{a|a≤2或a≥4}
C.{a|a≤0} D.{a|a≥8}
【答案】CD
【分析】由,得到a﹣1≥5或a+1≤1,由此能求出实数a的取值范围.
【详解】∵集合,满足,
∴或,解得或.
∴实数a的取值范围可以是{a|a≤0}或{a|a≥8}.
故选:CD.
集合,.
(1)若,,求实数a的值;
(2)从①,②,③这三个条件中选择一个作为已知条件,求实数a的取值范围.
【答案】(1)1
(2)条件选择见解析,
【分析】(1)由可知、,即可求出答案.
(2)三个条件中选择一个都可得,由此即可列出不等式组,即可求出答案.
(1)
因为,所以,
所以,得或.
当时,,不满足,故舍去;
当时,,满足题意.
故实数a的值为1.
(2)
方案一 选择条件①.
由,得,
所以,解得.
故实数a的取值范围是.
方案二 选择条件②.
由,得,
所以,解得.
故实数a的取值范围是.
方案三 选择条件③.
由,得,
所以解得.
故实数a的取值范围是.
设全集,集合,,
(1)求,
(2)若,求实数的取值范围.
【答案】(1),
(2)
【分析】(1)解一元二次不等式得集合M,按集合的交并补运算即可;
(2)利用集合间的包含关系,列不等式求解.
(1)
解:由得,
所以
由得,
所以
(2)
解:根据集合得,解得
同课章节目录
- 第1章 集合
- 1.1 集合的概念与表示
- 1.2 子集、全集、补集
- 1.3 交集、并集
- 第2章 常用逻辑用语
- 2.1 命题、定理、定义
- 2.2 充分条件、必要条件、冲要条件
- 2.3 全称量词命题与存在量词命题
- 第3章 不等式
- 3.1 不等式的基本性质
- 3.2 基本不等式
- 3.3 从函数观点看一元二次方程和一元二次不等式
- 第4章 指数与对数
- 4.1 指数
- 4.2 对数
- 第5章 函数概念与性质
- 5.1 函数的概念和图象
- 5.2 函数的表示方法
- 5.3 函数的单调性
- 5.4 函数的奇偶性
- 第6章 幂函数、指数函数和对数函数
- 6.1 幂函数
- 6.2 指数函数
- 6.3 对数函数
- 第7章 三角函数
- 7.1 角与弧度
- 7.2 三角函数概念
- 7.3 三角函数的图象和性质
- 7.4 三角函数应用
- 第8章 函数应用
- 8.1 二分法与求方程近似解
- 8.2 函数与数学模型
