24.1.2 垂直于弦的直径精准自测卷(含解析)
文档属性
| 名称 | 24.1.2 垂直于弦的直径精准自测卷(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-14 17:59:36 | ||
图片预览


文档简介
第二十四章 圆
24.1 圆的有关性质
24.1.2 垂直于弦的直径
夯基知识梳理
知识点1 圆的轴对称性
1.下列说法中,不正确的是 ( )
A.圆既是轴对称图形,又是中心对称图形 B.圆绕着它的圆心旋转任意角度,都能与自身重合
C.圆的对称轴有无数条,对称中心只有一个 D.圆的每一条直径都是它的对称轴
知识点2 垂径定理及其推论
2.(2022广东广州荔湾期中)如图,AB是⊙0的直径,CD为弦,CD⊥AB于点E,则下列结论中不一定成立的是 ( )
A.= B.= C.OE=BE D.CE=DE
3.下列说法:①平分弧的直径垂直平分弧所对的弦;②平分弦的直径平分弦所对的弧;③垂直于弦的直线必过圆心;④垂直于弦的直径平分弦所对的弧.其中正确的是 ( )
A.②③ B.①③ C.②④ D.①④
4.如图,已知AB、AC都是⊙O的弦,OM⊥AB,ON⊥AC,垂足分别为M,N,若MN=,则BC等于 ( )
A.5 B. C.2 D.
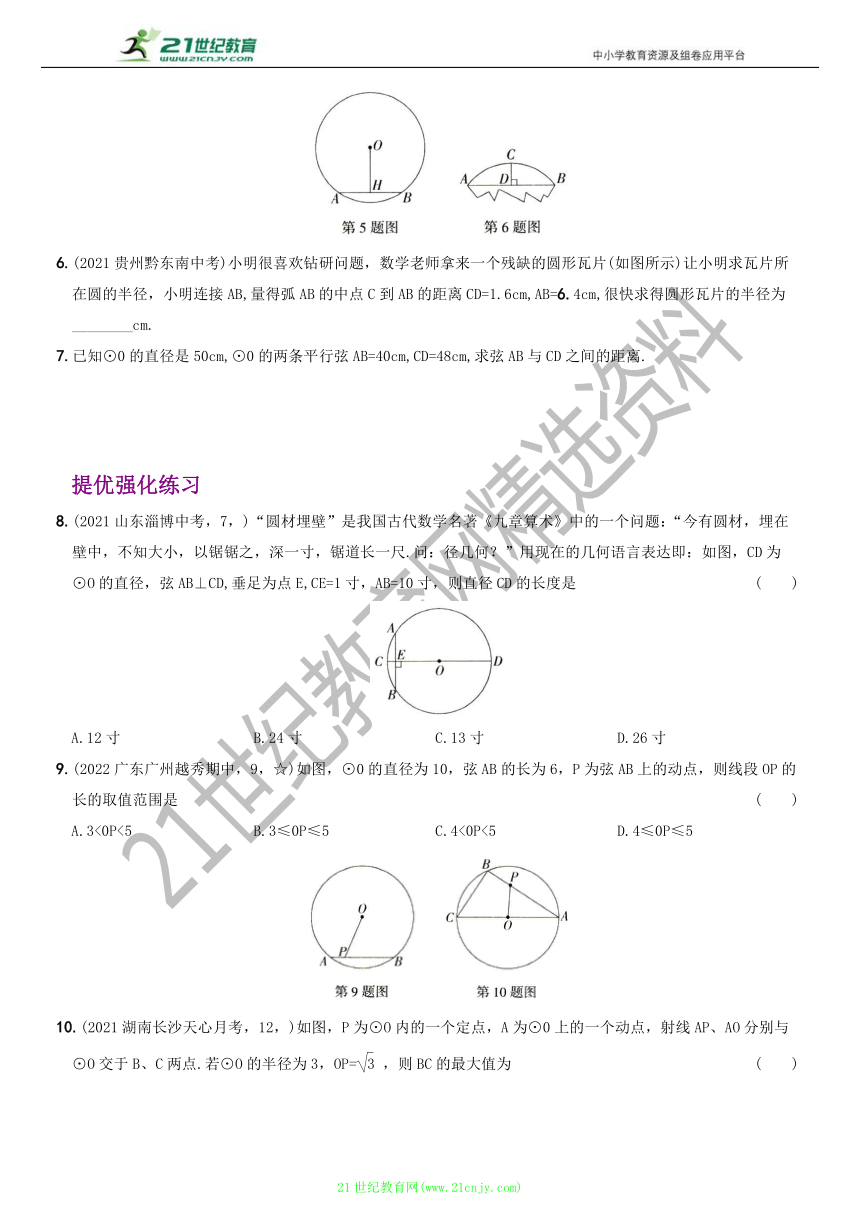
5.如图,在半径为5的⊙0中,弦AB=6,0H⊥AB于点H,则OH= ( )
A.3 B.4 C.5 D.6
6.(2021贵州黔东南中考)小明很喜欢钻研问题,数学老师拿来一个残缺的圆形瓦片(如图所示)让小明求瓦片所在圆的半径,小明连接AB,量得弧AB的中点C到AB的距离CD=1.6cm,AB=6.4cm,很快求得圆形瓦片的半径为________cm.
7.已知⊙0的直径是50cm,⊙0的两条平行弦AB=40cm,CD=48cm,求弦AB与CD之间的距离.
提优强化练习
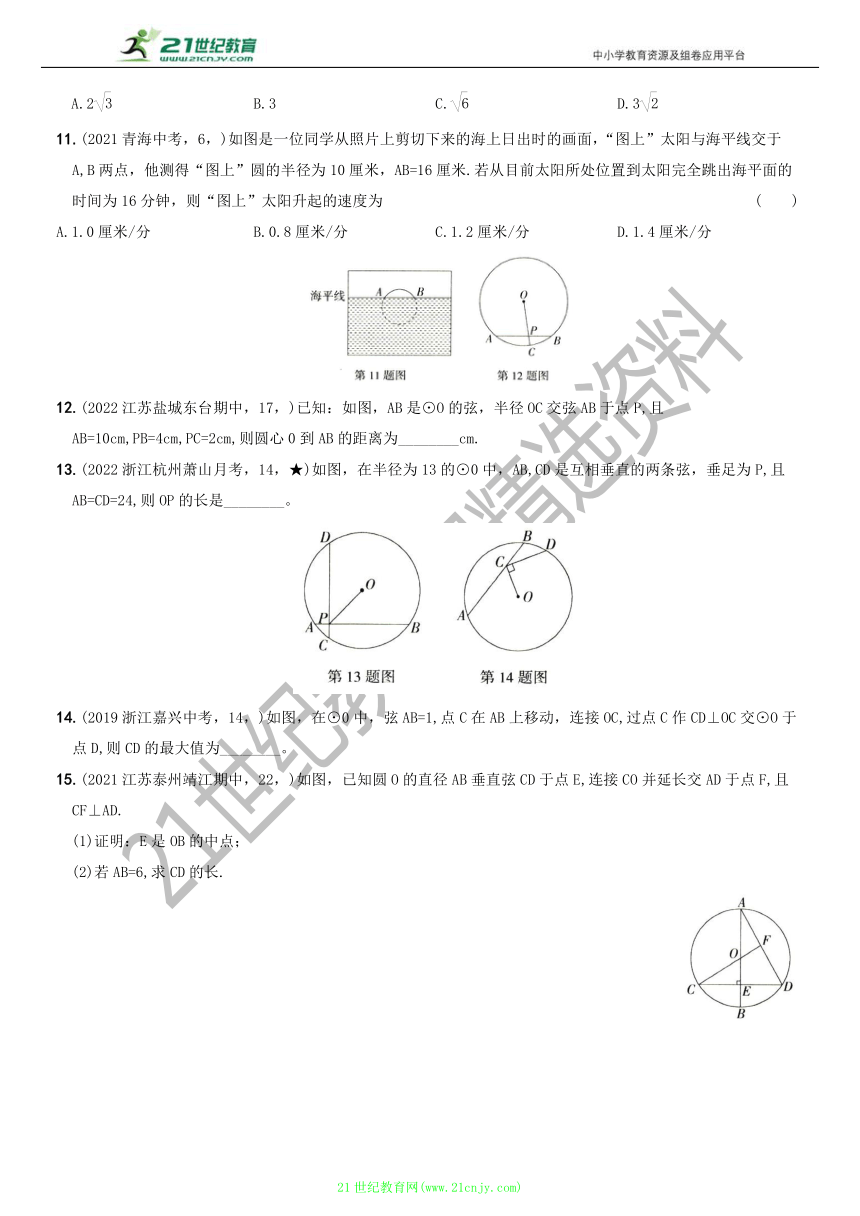
8.(2021山东淄博中考,7,)“圆材埋壁”是我国古代数学名著《九章算术》中的一个问题:“今有圆材,埋在壁中,不知大小,以锯锯之,深一寸,锯道长一尺.问:径几何?”用现在的几何语言表达即:如图,CD为⊙O的直径,弦AB⊥CD,垂足为点E,CE=1寸,AB=10寸,则直径CD的长度是 ( )
A.12寸 B.24寸 C.13寸 D.26寸
9.(2022广东广州越秀期中,9,☆)如图,⊙0的直径为10,弦AB的长为6,P为弦AB上的动点,则线段OP的长的取值范围是 ( )
A.3<0P<5 B.3≤0P≤5 C.4<0P<5 D.4≤0P≤5
10.(2021湖南长沙天心月考,12,)如图,P为⊙O内的一个定点,A为⊙0上的一个动点,射线AP、AO分别与⊙O交于B、C两点.若⊙O的半径为3,OP=,则BC的最大值为 ( )
A.2 B.3 C. D.3
11.(2021青海中考,6,)如图是一位同学从照片上剪切下来的海上日出时的画面,“图上”太阳与海平线交于A,B两点,他测得“图上”圆的半径为10厘米,AB=16厘米.若从目前太阳所处位置到太阳完全跳出海平面的时间为16分钟,则“图上”太阳升起的速度为 ( )
A.1.0厘米/分 B.0.8厘米/分 C.1.2厘米/分 D.1.4厘米/分
12.(2022江苏盐城东台期中,17,)已知:如图,AB是⊙O的弦,半径OC交弦AB于点P,且AB=10cm,PB=4cm,PC=2cm,则圆心0到AB的距离为________cm.
13.(2022浙江杭州萧山月考,14,★)如图,在半径为13的⊙0中,AB,CD是互相垂直的两条弦,垂足为P,且AB=CD=24,则OP的长是________。
14.(2019浙江嘉兴中考,14,)如图,在⊙0中,弦AB=1,点C在AB上移动,连接OC,过点C作CD⊥OC交⊙O于点D,则CD的最大值为________。
15.(2021江苏泰州靖江期中,22,)如图,已知圆O的直径AB垂直弦CD于点E,连接CO并延长交AD于点F,且CF⊥AD.
(1)证明:E是OB的中点;
(2)若AB=6,求CD的长.
素养能力培优
16.[数学运算]如图,在平面直角坐标系中,以原点0为圆心的圆过点A(0,3),直线y=kx-3k+4(k≠0)与⊙0交于B,C两点,则弦BC的长的最小值为________。
17.[逻辑推理]如图,已知⊙0的半径为2.弦AB的长度为2,点C是⊙0上一动点,若△ABC为等腰三角形,则BC2=____________________
【参考答案及解析】
24.1.2垂直于弦的直径
夯基知识梳理
1.D 圆既是轴对称图形,又是中心对称图形,所以A说法正确;圆是一个特殊的中心对称图形,它绕着圆心旋转任意角度都能与自身重合,所以B说法正确;圆的对称轴是过圆心的直线,这样的直线有无数条,对称中心只有一个,是圆心,所以说法正确;直径是线段而不是直线,不能说直径是圆的对称轴,所以D说法错误.
2.C ∵AB是⊙O的直径,CD为弦,CD⊥AB于点E,∴=,=,CE=DE,但OE不一定等于BE,故选项A、B、D成立,选项C不一定成立.
3.D 平分弦(不是直径)的直径平分弦所对的弧,故②错误.垂直于弦且平分弦的直线必过圆心,故③错误①④正确.故选D.
4.C ·∵OM⊥AB,ON⊥AC,垂足分别为M、N,∴M、N分别是AB、AC的中点,∴MN是△ABC的中位线,∴BC=2MN=2.故选C.
5.B 如图,连接0A,∵AB=6,OH⊥AB,∴AH=BH=AB=3,∠OHA=90°,在Rt△OHA中,由勾股定理得0H===4.故选B.
6.【答案】4
【解析】如图,设圆心为O,连接OA、OC,∵C为的中点,∴OC⊥AB,又CD⊥AB,∴C、D、O三点共线,∴AD=BD=AB=×6.4=3.2(cm).设⊙0的半径为rcm22则0D=(r-1.6)cm,在Rt△OAD中,(r-1.6)2+3.22=r2,解得r=4,所以圆形瓦片的半径为4cm.
7.【解析】本题有两种情况:
(1)当AB,CD在圆心0的同侧时,如图1所示,作OF⊥AB于F,交CD于E,连接OA,OC,则0A=0C=25cm.∵AB∥CD,∴OE⊥CD,由垂径定理知AF=AB=20(cm),CE=CD=24(cm),∴0E==7(cm),0F==15(cm),∴弦AB与CD之间的距离EF=15-7=8(cm).
(2)当AB,CD在圆心0的异侧时,如图2所示,同(1)可知0E=7cm,0F=15cm,∴弦AB与CD之间的距离EF=15+7=22(cm).综上,弦AB与CD之间的距离为8cm或22cm.
提优强化练习
8.D 如图,连接OA,∵AB⊥CD,且AB=10寸,∴AE=BE=5寸.设⊙0的半径OA的长为x寸,则OC=OD=x寸.∵CE=1寸,∴OE=(x-1)寸.在Rt△AOE中,由勾股定理得x2-(x-1)2=52,化简得x2-x2+2x-1=25,即2x=26,∴CD=26寸,即直径CD的长为26寸.
9.D 如图,连接OA,过点O作OH⊥AB于H,则AH=HB=AB=3.⊙0的直径为10,0A=5,由勾股定理得,0H===4,当点P与点A(或点B)重合时,OP的长度最大,当点P与点H重合时,OP的长度最小,∴线段0P的长的取值范围是4≤0P≤5.
10.A 如图,过点0作0E⊥AB于E,∵0为圆心,∴AE=BE,∵OA=OC,∴OE为△ABC的中位线,∴OE=BC.∵OE≤OP,∴BC≤2OP,∴当E、P重合,即OP⊥AB时,BC取得最大值,∴BC的最大值为2OP=2.故选A.
11.A 设“图上”圆的圆心为0,连接0A,作0D⊥AB于D,延长DO交圆于点C,如图所示:
∵AB=16厘米,∴AD=AB=8(厘米),∵0A=10厘米,∴0D===6(厘米),∴DC=0C+0D=10+6=16(厘米),∵太阳从所处位置到完全跳出海平面的时间为16分钟,∴“图上”太阳升起的速度=16÷16=1.0(厘米/分),故选A.
12.【答案】2
【解析】如图,连接OA,作OD⊥AB于D,则AD=BD=AB=5(cm),DP=BD-PB=1(cm).设0A=0C=rcm,在Rt△AOD和Rt△OPD中,由勾股定理得OD2=0A2-AD2=0P2-DP2,即r2-52=(r-2)2-12,解得r=7,即0A=7cm,∴0D==2(cm),即圆心0到AB的距离为2cm.
13.【答案】5
【解析】如图,作OM⊥AB于M,ON⊥CD于N,连接OB,OD,∴DN=CD,BM=AB,∵AB=CD=24,∴DN=BM=12,∴0M=0N==5.∵弦AB、CD互相垂直,∴∠DPB=90°.∵0M⊥AB于M,ON⊥CD于N,∴∠OMP=∠ONP=90°,∴四边形MONP是矩形.∵OM=ON,∴四边形MONP是正方形,∴OP=5.
14.【答案】
【解析】如图,连接0D,∵CD⊥0C,∴∠DCO=90°,∴CD==(r为圆0的半径),当OC的长最小时,CD的长最大,而OC⊥AB时,OC的长最小,此时D、B两点重合,CD=CB=AB=×1=,∴CD的最大值为
15.【解析】
(1)证明:如图,连接AC,∵直径AB垂直弦CD于点E,∴CE=DE,∴AC=AD.∵CF⊥AD,且CF经过圆心O,∴AF=DF,∴CF所在直线是AD的垂直平分线,∴AC=CD,∴AC=AD=CD,即△ACD是等边三角形,∴∠FCD=30∴在R△COE中,OE=OC,OE=OB,∴点E为OB的中点.
(2)∵AB=6,∴0B=0C=AB=3.∵点E为OB的中点,∴BE=OE,∴OE=∴CE==∴CD=2CE=3.
素养能力培优
16.【答案】4
【解析】如图,连接OB,过点O作OD⊥BC于点D,∴BC=2BD=20B2-0D2,∵以原点0为圆心的圆过点A(0,3),∴圆的半径为3,∴0B=3,∴BC=2,∵直线y=kx-3k+4必过点(3,4),∴点D的坐标为(3,4)时,0D的长度最大,弦BC的长度最小,此时0D=5,BC=2=2=4,∴弦BC的长的最小值为4.
17.【答案】8±4或12或4
【解析】分以下两种情况:①如图1,以AB为底边时,存在△ABC1与△ABC2,连接C1C2、AO,C1C2与AB交于点D,则C1C2垂直平分AB,∴C1C2过圆心O,AD=AB=1.∵0A=2,∴0D==,∴C1D=2+,C2D=2-,∴BC12=(2+)2+12=8+4,BC22=(2-)2+12=8-4.②如图2,以AB为腰时,存在△ABC3与△ABC4,则AC3=BC4=AB=2,连接OC3、BO、AO,AO交BC3于E,则BC42=4,∵OC3=OB,AC3=AB,∴OA垂直平分BC3,∴BE=C3E,OA⊥BC3,∵OC3=AO=AC3=2,∴△AC3O是等边三角形,∴∠EOC3=60°,∵0A⊥BC3,∴∠OC3E=30°,∴0E=1,C3E=,∴BC3=2,∴BC32=(2)2=12.综上,BC2=8±4或12或4.
21世纪教育网(www.21cnjy.com)
24.1 圆的有关性质
24.1.2 垂直于弦的直径
夯基知识梳理
知识点1 圆的轴对称性
1.下列说法中,不正确的是 ( )
A.圆既是轴对称图形,又是中心对称图形 B.圆绕着它的圆心旋转任意角度,都能与自身重合
C.圆的对称轴有无数条,对称中心只有一个 D.圆的每一条直径都是它的对称轴
知识点2 垂径定理及其推论
2.(2022广东广州荔湾期中)如图,AB是⊙0的直径,CD为弦,CD⊥AB于点E,则下列结论中不一定成立的是 ( )
A.= B.= C.OE=BE D.CE=DE
3.下列说法:①平分弧的直径垂直平分弧所对的弦;②平分弦的直径平分弦所对的弧;③垂直于弦的直线必过圆心;④垂直于弦的直径平分弦所对的弧.其中正确的是 ( )
A.②③ B.①③ C.②④ D.①④
4.如图,已知AB、AC都是⊙O的弦,OM⊥AB,ON⊥AC,垂足分别为M,N,若MN=,则BC等于 ( )
A.5 B. C.2 D.
5.如图,在半径为5的⊙0中,弦AB=6,0H⊥AB于点H,则OH= ( )
A.3 B.4 C.5 D.6
6.(2021贵州黔东南中考)小明很喜欢钻研问题,数学老师拿来一个残缺的圆形瓦片(如图所示)让小明求瓦片所在圆的半径,小明连接AB,量得弧AB的中点C到AB的距离CD=1.6cm,AB=6.4cm,很快求得圆形瓦片的半径为________cm.
7.已知⊙0的直径是50cm,⊙0的两条平行弦AB=40cm,CD=48cm,求弦AB与CD之间的距离.
提优强化练习
8.(2021山东淄博中考,7,)“圆材埋壁”是我国古代数学名著《九章算术》中的一个问题:“今有圆材,埋在壁中,不知大小,以锯锯之,深一寸,锯道长一尺.问:径几何?”用现在的几何语言表达即:如图,CD为⊙O的直径,弦AB⊥CD,垂足为点E,CE=1寸,AB=10寸,则直径CD的长度是 ( )
A.12寸 B.24寸 C.13寸 D.26寸
9.(2022广东广州越秀期中,9,☆)如图,⊙0的直径为10,弦AB的长为6,P为弦AB上的动点,则线段OP的长的取值范围是 ( )
A.3<0P<5 B.3≤0P≤5 C.4<0P<5 D.4≤0P≤5
10.(2021湖南长沙天心月考,12,)如图,P为⊙O内的一个定点,A为⊙0上的一个动点,射线AP、AO分别与⊙O交于B、C两点.若⊙O的半径为3,OP=,则BC的最大值为 ( )
A.2 B.3 C. D.3
11.(2021青海中考,6,)如图是一位同学从照片上剪切下来的海上日出时的画面,“图上”太阳与海平线交于A,B两点,他测得“图上”圆的半径为10厘米,AB=16厘米.若从目前太阳所处位置到太阳完全跳出海平面的时间为16分钟,则“图上”太阳升起的速度为 ( )
A.1.0厘米/分 B.0.8厘米/分 C.1.2厘米/分 D.1.4厘米/分
12.(2022江苏盐城东台期中,17,)已知:如图,AB是⊙O的弦,半径OC交弦AB于点P,且AB=10cm,PB=4cm,PC=2cm,则圆心0到AB的距离为________cm.
13.(2022浙江杭州萧山月考,14,★)如图,在半径为13的⊙0中,AB,CD是互相垂直的两条弦,垂足为P,且AB=CD=24,则OP的长是________。
14.(2019浙江嘉兴中考,14,)如图,在⊙0中,弦AB=1,点C在AB上移动,连接OC,过点C作CD⊥OC交⊙O于点D,则CD的最大值为________。
15.(2021江苏泰州靖江期中,22,)如图,已知圆O的直径AB垂直弦CD于点E,连接CO并延长交AD于点F,且CF⊥AD.
(1)证明:E是OB的中点;
(2)若AB=6,求CD的长.
素养能力培优
16.[数学运算]如图,在平面直角坐标系中,以原点0为圆心的圆过点A(0,3),直线y=kx-3k+4(k≠0)与⊙0交于B,C两点,则弦BC的长的最小值为________。
17.[逻辑推理]如图,已知⊙0的半径为2.弦AB的长度为2,点C是⊙0上一动点,若△ABC为等腰三角形,则BC2=____________________
【参考答案及解析】
24.1.2垂直于弦的直径
夯基知识梳理
1.D 圆既是轴对称图形,又是中心对称图形,所以A说法正确;圆是一个特殊的中心对称图形,它绕着圆心旋转任意角度都能与自身重合,所以B说法正确;圆的对称轴是过圆心的直线,这样的直线有无数条,对称中心只有一个,是圆心,所以说法正确;直径是线段而不是直线,不能说直径是圆的对称轴,所以D说法错误.
2.C ∵AB是⊙O的直径,CD为弦,CD⊥AB于点E,∴=,=,CE=DE,但OE不一定等于BE,故选项A、B、D成立,选项C不一定成立.
3.D 平分弦(不是直径)的直径平分弦所对的弧,故②错误.垂直于弦且平分弦的直线必过圆心,故③错误①④正确.故选D.
4.C ·∵OM⊥AB,ON⊥AC,垂足分别为M、N,∴M、N分别是AB、AC的中点,∴MN是△ABC的中位线,∴BC=2MN=2.故选C.
5.B 如图,连接0A,∵AB=6,OH⊥AB,∴AH=BH=AB=3,∠OHA=90°,在Rt△OHA中,由勾股定理得0H===4.故选B.
6.【答案】4
【解析】如图,设圆心为O,连接OA、OC,∵C为的中点,∴OC⊥AB,又CD⊥AB,∴C、D、O三点共线,∴AD=BD=AB=×6.4=3.2(cm).设⊙0的半径为rcm22则0D=(r-1.6)cm,在Rt△OAD中,(r-1.6)2+3.22=r2,解得r=4,所以圆形瓦片的半径为4cm.
7.【解析】本题有两种情况:
(1)当AB,CD在圆心0的同侧时,如图1所示,作OF⊥AB于F,交CD于E,连接OA,OC,则0A=0C=25cm.∵AB∥CD,∴OE⊥CD,由垂径定理知AF=AB=20(cm),CE=CD=24(cm),∴0E==7(cm),0F==15(cm),∴弦AB与CD之间的距离EF=15-7=8(cm).
(2)当AB,CD在圆心0的异侧时,如图2所示,同(1)可知0E=7cm,0F=15cm,∴弦AB与CD之间的距离EF=15+7=22(cm).综上,弦AB与CD之间的距离为8cm或22cm.
提优强化练习
8.D 如图,连接OA,∵AB⊥CD,且AB=10寸,∴AE=BE=5寸.设⊙0的半径OA的长为x寸,则OC=OD=x寸.∵CE=1寸,∴OE=(x-1)寸.在Rt△AOE中,由勾股定理得x2-(x-1)2=52,化简得x2-x2+2x-1=25,即2x=26,∴CD=26寸,即直径CD的长为26寸.
9.D 如图,连接OA,过点O作OH⊥AB于H,则AH=HB=AB=3.⊙0的直径为10,0A=5,由勾股定理得,0H===4,当点P与点A(或点B)重合时,OP的长度最大,当点P与点H重合时,OP的长度最小,∴线段0P的长的取值范围是4≤0P≤5.
10.A 如图,过点0作0E⊥AB于E,∵0为圆心,∴AE=BE,∵OA=OC,∴OE为△ABC的中位线,∴OE=BC.∵OE≤OP,∴BC≤2OP,∴当E、P重合,即OP⊥AB时,BC取得最大值,∴BC的最大值为2OP=2.故选A.
11.A 设“图上”圆的圆心为0,连接0A,作0D⊥AB于D,延长DO交圆于点C,如图所示:
∵AB=16厘米,∴AD=AB=8(厘米),∵0A=10厘米,∴0D===6(厘米),∴DC=0C+0D=10+6=16(厘米),∵太阳从所处位置到完全跳出海平面的时间为16分钟,∴“图上”太阳升起的速度=16÷16=1.0(厘米/分),故选A.
12.【答案】2
【解析】如图,连接OA,作OD⊥AB于D,则AD=BD=AB=5(cm),DP=BD-PB=1(cm).设0A=0C=rcm,在Rt△AOD和Rt△OPD中,由勾股定理得OD2=0A2-AD2=0P2-DP2,即r2-52=(r-2)2-12,解得r=7,即0A=7cm,∴0D==2(cm),即圆心0到AB的距离为2cm.
13.【答案】5
【解析】如图,作OM⊥AB于M,ON⊥CD于N,连接OB,OD,∴DN=CD,BM=AB,∵AB=CD=24,∴DN=BM=12,∴0M=0N==5.∵弦AB、CD互相垂直,∴∠DPB=90°.∵0M⊥AB于M,ON⊥CD于N,∴∠OMP=∠ONP=90°,∴四边形MONP是矩形.∵OM=ON,∴四边形MONP是正方形,∴OP=5.
14.【答案】
【解析】如图,连接0D,∵CD⊥0C,∴∠DCO=90°,∴CD==(r为圆0的半径),当OC的长最小时,CD的长最大,而OC⊥AB时,OC的长最小,此时D、B两点重合,CD=CB=AB=×1=,∴CD的最大值为
15.【解析】
(1)证明:如图,连接AC,∵直径AB垂直弦CD于点E,∴CE=DE,∴AC=AD.∵CF⊥AD,且CF经过圆心O,∴AF=DF,∴CF所在直线是AD的垂直平分线,∴AC=CD,∴AC=AD=CD,即△ACD是等边三角形,∴∠FCD=30∴在R△COE中,OE=OC,OE=OB,∴点E为OB的中点.
(2)∵AB=6,∴0B=0C=AB=3.∵点E为OB的中点,∴BE=OE,∴OE=∴CE==∴CD=2CE=3.
素养能力培优
16.【答案】4
【解析】如图,连接OB,过点O作OD⊥BC于点D,∴BC=2BD=20B2-0D2,∵以原点0为圆心的圆过点A(0,3),∴圆的半径为3,∴0B=3,∴BC=2,∵直线y=kx-3k+4必过点(3,4),∴点D的坐标为(3,4)时,0D的长度最大,弦BC的长度最小,此时0D=5,BC=2=2=4,∴弦BC的长的最小值为4.
17.【答案】8±4或12或4
【解析】分以下两种情况:①如图1,以AB为底边时,存在△ABC1与△ABC2,连接C1C2、AO,C1C2与AB交于点D,则C1C2垂直平分AB,∴C1C2过圆心O,AD=AB=1.∵0A=2,∴0D==,∴C1D=2+,C2D=2-,∴BC12=(2+)2+12=8+4,BC22=(2-)2+12=8-4.②如图2,以AB为腰时,存在△ABC3与△ABC4,则AC3=BC4=AB=2,连接OC3、BO、AO,AO交BC3于E,则BC42=4,∵OC3=OB,AC3=AB,∴OA垂直平分BC3,∴BE=C3E,OA⊥BC3,∵OC3=AO=AC3=2,∴△AC3O是等边三角形,∴∠EOC3=60°,∵0A⊥BC3,∴∠OC3E=30°,∴0E=1,C3E=,∴BC3=2,∴BC32=(2)2=12.综上,BC2=8±4或12或4.
21世纪教育网(www.21cnjy.com)
同课章节目录
