24.1.3 弧、弦、圆心角精准自测卷(含解析)
文档属性
| 名称 | 24.1.3 弧、弦、圆心角精准自测卷(含解析) |
|
|
| 格式 | docx | ||
| 文件大小 | 892.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-14 00:00:00 | ||
图片预览



文档简介
第二十四章 圆
24.1 圆的有关性质
24.1.3 弧、弦、圆心角
夯基知识梳理
知识点1 弧、弦、圆心角之间的关系
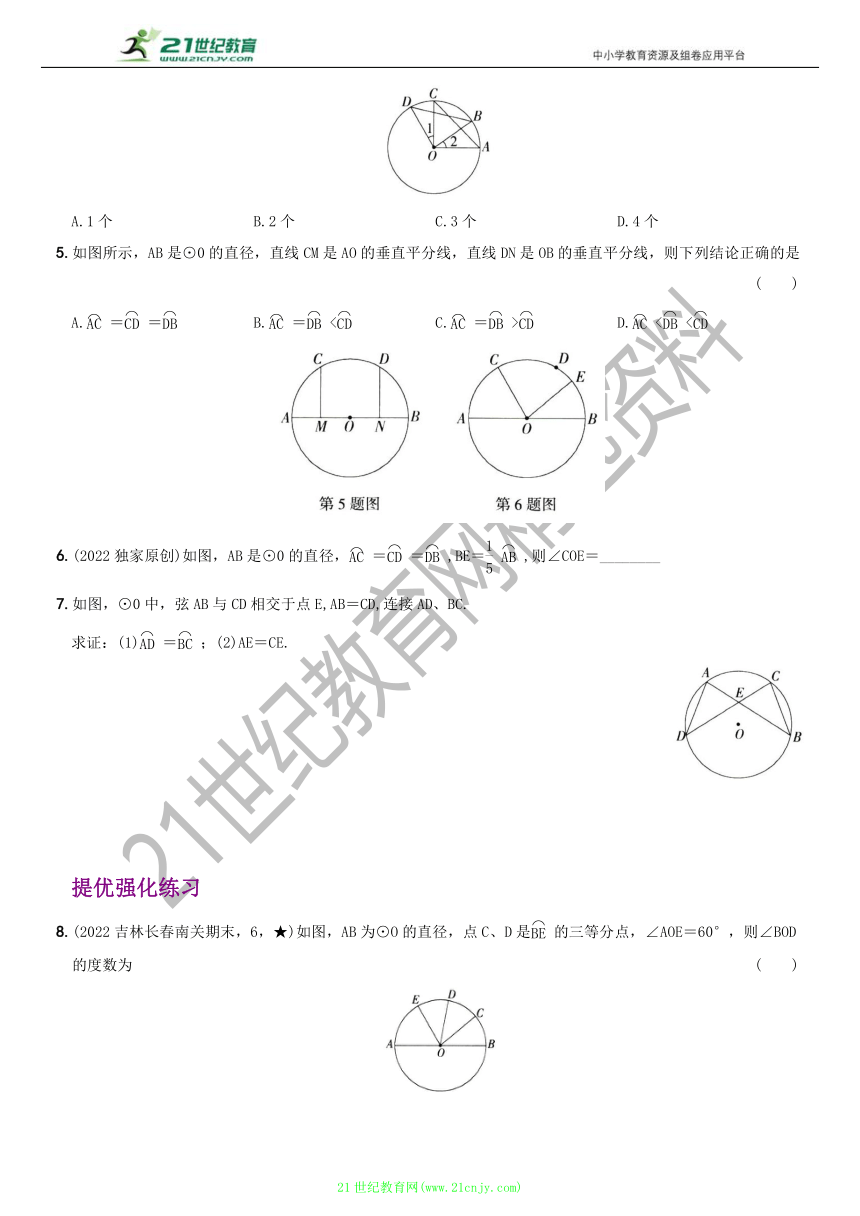
1.(2022独家原创)如图,点A、B、Q在⊙O上,点P在⊙O外,点M在⊙O内,则图中标记的四个角中,是圆心角的是 ( )
A.∠APB B.∠AQB C.∠AOB D.∠AMB
2.观察下列图形及相应的推理,其中正确的是 ( )
A.①② B.③④ C.①③ D.②④
3.如图所示,在⊙0中,AB=AC,∠A=30°,则∠B= ( )
A.150° B.75° C.60° D.15°
4.如图,A、B、C、D是⊙0上的点,∠1=∠2,则下列
结论:①=;②=;③=; ④∠BOD=∠AOC.其中正确的有 ( )
A.1个 B.2个 C.3个 D.4个
5.如图所示,AB是⊙0的直径,直线CM是AO的垂直平分线,直线DN是OB的垂直平分线,则下列结论正确的是 ( )
A.== B.=< C.=> D.<<
6.(2022独家原创)如图,AB是⊙0的直径,==,BE=,则∠COE=________
7.如图,⊙0中,弦AB与CD相交于点E,AB=CD,连接AD、BC.
求证:(1)=;(2)AE=CE.
提优强化练习
8.(2022吉林长春南关期末,6,★)如图,AB为⊙O的直径,点C、D是的三等分点,∠AOE=60°,则∠BOD的度数为 ( )
A.40° B.60° C.80° D.120°
9.(2022四川绵阳江油期末,10,)如图,AB为⊙O的直径,点D是的中点,过点D作DE⊥AB于点E,延长DE交⊙O于点F,若AE=3,⊙0的直径为15,则AC的长为 ( )
A.10 B.13 C.12 D.11
10.如图,AB是⊙O的直径,C、D为半圆的三等分点,CE⊥AB于点E,则∠ACE的度数为________.
11.(2022辽宁鞍山立山期中,10,)如图,半径为5的⊙A中,弦BC、ED所对的圆心角分别是∠BAC、∠EAD,已知DE=6,∠BAC+∠EAD=180°,则圆心A到弦BC的距离等于________。
12.(2021陕西西安雁塔期中,23,)如图,AB为⊙O的弦,半径OC,OD分别交AB于点E,F,且=.
(1)求证:AE=BF;
(2)作半径ON⊥AB于点M,若AB=12,MN=3,求OM的长.
素养能力培优
13.[逻辑推理]如图,C、D三等分以0为圆心的,连MN、CD、OC、OD、OM,下列结论错误的是 ( )
A.∠COM=∠COD B.若OM=MN,则∠COD=20°
C.MN//CD D.MN=3CD
14.[逻辑推理]如图所示,MN为⊙0的直径,点A是上靠近点N的三等分点,点B是的中点,点P是直径MN上一动点,若⊙O的直径为2,则AP+BP的最小值是____________________。
【参考答案及解析】
24.1.3弧、弦、圆心角
夯基知识梳理
1.C 顶点在圆心的角叫做圆心角,所以∠AOB是圆心角,其他3个角都不是圆心角.
2.C ①中,在同圆或等圆中,如果两个圆心角、两条弧、两条弦中有一组量相等,那么相应的其余各组量都分别相等,故①正确;③中,∵=,∴+=+,即=,∴AB=CD,故③正确;②和④中,不是在同圆或等圆中,故②④不正确.
3.B ∵在⊙O中,=,∴AB=AC,∴∠B=∠C,又∠A=30°,∴∠B==75°.
4.D ∵∠1=∠2,∴=,∠BOD=∠AOC,∴=,∴AC=BD,∴①②③④正确,故选D.
5.A 如图,连接AC,OC,OD,BD,∵直线CM是AO的垂直平分线,直线DN是OB的垂直平分线,∴AC=OC,BD=OD.∵OC=OD=OA=OB,∴△AOC,△BOD都是等边三角形,∴∠AOC=∠BOD=60.∵AB是⊙0的直径,∴∠COD=60°,∴∠AOC=∠COD=∠BOD,∴==.故选A.
6.【答案】84°
【解析】∵AB是⊙O的直径,==,∴∠AOC=×180°=60°,∵BE=÷AB,∴∠BOE=×180°=36°,∴∠COE=180°-60°-36°=84°
7.证明
(1)∵AB=CD,∴=,即+=+,∴=
(2)如图,连接AC,=,∴AD=BC.又∵CD=AB,AC=AC,∴△ADC≌△CBA(SSS),∴∠ACD=∠CAB.∴AE=CE.
提优强化练习
8.C ∵∠AOE=60°,∴∠BOE=180°-∠AOE=120°∵点C、D是BE的三等分点,∴∠BOD=×120°=80°
9.C 如图,连接OF,∵DE⊥AB,AB为⊙O的直径,∴DE=EF,=,∵D为的中点,∴=DC,∴=,∴AC=DF.∵⊙0的直径为15,∴OF=OA=∵AE=3,∴OE=OA-AE=,在Rt△OEF中,由勾股定理得EF===6,∴DE=EF=6,∴AC=DF=DE+EF=6+6=12.
10.【答案】30°
【解析】如图,连接OC.∵AB是直径,==,∴∠AOC=∠COD=∠DOB=60.O A=OC,∴△AOC是等边三角形,∴∠A=60°,∵CE⊥OA,∴∠AEC=90°,∴∠ACE=90°-60°=30°
11.【答案】3
【解析】如图,作AH⊥BC于H,作直径CF,连接BF.∵∠BAC+∠EAD=180°,∠BAC+∠BAF=180°,∴∠BAF=∠DAE,∴BF=DE,∴==6.A H⊥BC,∴CH=BH,CA=AF,∴AH为△CBF的中位线,∴AH=BF=3.∴点A到弦BC的距离为3.
12.
【解析】
(1)证明:如图1,连接OA、OB,∵OA=OB,∴∠A=∠B.∵=,∴∠AOE=∠BOF在△AOE和△BOF中,,∴△AOE≌△BOF(ASA),∴AE=BF.
(2)如图2,连接OA,∵OM⊥AB,∴AM=AB=6,设OM=x,则OA=ON=x+3,在Rt△AOM中,由勾股定理得62+x2=(x+3)2,解得x=4.5,∴OM=4.5.
素养能力培优
13.D 如图,连接ON、MC、DN,过点O作OE⊥CD交于点E,∵=,∴∠COM=∠COD,故A正确;当OM=MN时,∵OM=ON,∴OM=ON=MN,∴△OMN为等边三角形,∴∠MON=60°,∵==,∴∠COM=∠COD=∠DON,∴∠COD=20°,故B正确:OE⊥CD,∴=,∴=,∴OE⊥MN,∴MN∥CD,故C正确;∵==,∴MC=CD=DN,∵MC+CD+DN>MN,∴MN<3CD,故D错误.
14.【答案】
【解析】如图,作点B关于直线MN的对称点B′,连接AB′交MN于点P′,连接BP′,OB′,OB.∵点B和点B′关于直线MN对称,∴P′B=P′B′,=,AP′+BP′=AP′+B′P′=AB′,易知点P位于点P′处时,AP+BP的值最小.∵点A是上靠近点N的三等分点,点B是的中点,=,∴∠AON=180°÷3=60°,∠B′ON=∠BON=∠AON=30°,∴∠AOB′=∠AON+∠B′ON=90.O A=OB′=1,∴AB′=,故AP+BP的最小值为.
21世纪教育网(www.21cnjy.com)
24.1 圆的有关性质
24.1.3 弧、弦、圆心角
夯基知识梳理
知识点1 弧、弦、圆心角之间的关系
1.(2022独家原创)如图,点A、B、Q在⊙O上,点P在⊙O外,点M在⊙O内,则图中标记的四个角中,是圆心角的是 ( )
A.∠APB B.∠AQB C.∠AOB D.∠AMB
2.观察下列图形及相应的推理,其中正确的是 ( )
A.①② B.③④ C.①③ D.②④
3.如图所示,在⊙0中,AB=AC,∠A=30°,则∠B= ( )
A.150° B.75° C.60° D.15°
4.如图,A、B、C、D是⊙0上的点,∠1=∠2,则下列
结论:①=;②=;③=; ④∠BOD=∠AOC.其中正确的有 ( )
A.1个 B.2个 C.3个 D.4个
5.如图所示,AB是⊙0的直径,直线CM是AO的垂直平分线,直线DN是OB的垂直平分线,则下列结论正确的是 ( )
A.== B.=< C.=> D.<<
6.(2022独家原创)如图,AB是⊙0的直径,==,BE=,则∠COE=________
7.如图,⊙0中,弦AB与CD相交于点E,AB=CD,连接AD、BC.
求证:(1)=;(2)AE=CE.
提优强化练习
8.(2022吉林长春南关期末,6,★)如图,AB为⊙O的直径,点C、D是的三等分点,∠AOE=60°,则∠BOD的度数为 ( )
A.40° B.60° C.80° D.120°
9.(2022四川绵阳江油期末,10,)如图,AB为⊙O的直径,点D是的中点,过点D作DE⊥AB于点E,延长DE交⊙O于点F,若AE=3,⊙0的直径为15,则AC的长为 ( )
A.10 B.13 C.12 D.11
10.如图,AB是⊙O的直径,C、D为半圆的三等分点,CE⊥AB于点E,则∠ACE的度数为________.
11.(2022辽宁鞍山立山期中,10,)如图,半径为5的⊙A中,弦BC、ED所对的圆心角分别是∠BAC、∠EAD,已知DE=6,∠BAC+∠EAD=180°,则圆心A到弦BC的距离等于________。
12.(2021陕西西安雁塔期中,23,)如图,AB为⊙O的弦,半径OC,OD分别交AB于点E,F,且=.
(1)求证:AE=BF;
(2)作半径ON⊥AB于点M,若AB=12,MN=3,求OM的长.
素养能力培优
13.[逻辑推理]如图,C、D三等分以0为圆心的,连MN、CD、OC、OD、OM,下列结论错误的是 ( )
A.∠COM=∠COD B.若OM=MN,则∠COD=20°
C.MN//CD D.MN=3CD
14.[逻辑推理]如图所示,MN为⊙0的直径,点A是上靠近点N的三等分点,点B是的中点,点P是直径MN上一动点,若⊙O的直径为2,则AP+BP的最小值是____________________。
【参考答案及解析】
24.1.3弧、弦、圆心角
夯基知识梳理
1.C 顶点在圆心的角叫做圆心角,所以∠AOB是圆心角,其他3个角都不是圆心角.
2.C ①中,在同圆或等圆中,如果两个圆心角、两条弧、两条弦中有一组量相等,那么相应的其余各组量都分别相等,故①正确;③中,∵=,∴+=+,即=,∴AB=CD,故③正确;②和④中,不是在同圆或等圆中,故②④不正确.
3.B ∵在⊙O中,=,∴AB=AC,∴∠B=∠C,又∠A=30°,∴∠B==75°.
4.D ∵∠1=∠2,∴=,∠BOD=∠AOC,∴=,∴AC=BD,∴①②③④正确,故选D.
5.A 如图,连接AC,OC,OD,BD,∵直线CM是AO的垂直平分线,直线DN是OB的垂直平分线,∴AC=OC,BD=OD.∵OC=OD=OA=OB,∴△AOC,△BOD都是等边三角形,∴∠AOC=∠BOD=60.∵AB是⊙0的直径,∴∠COD=60°,∴∠AOC=∠COD=∠BOD,∴==.故选A.
6.【答案】84°
【解析】∵AB是⊙O的直径,==,∴∠AOC=×180°=60°,∵BE=÷AB,∴∠BOE=×180°=36°,∴∠COE=180°-60°-36°=84°
7.证明
(1)∵AB=CD,∴=,即+=+,∴=
(2)如图,连接AC,=,∴AD=BC.又∵CD=AB,AC=AC,∴△ADC≌△CBA(SSS),∴∠ACD=∠CAB.∴AE=CE.
提优强化练习
8.C ∵∠AOE=60°,∴∠BOE=180°-∠AOE=120°∵点C、D是BE的三等分点,∴∠BOD=×120°=80°
9.C 如图,连接OF,∵DE⊥AB,AB为⊙O的直径,∴DE=EF,=,∵D为的中点,∴=DC,∴=,∴AC=DF.∵⊙0的直径为15,∴OF=OA=∵AE=3,∴OE=OA-AE=,在Rt△OEF中,由勾股定理得EF===6,∴DE=EF=6,∴AC=DF=DE+EF=6+6=12.
10.【答案】30°
【解析】如图,连接OC.∵AB是直径,==,∴∠AOC=∠COD=∠DOB=60.O A=OC,∴△AOC是等边三角形,∴∠A=60°,∵CE⊥OA,∴∠AEC=90°,∴∠ACE=90°-60°=30°
11.【答案】3
【解析】如图,作AH⊥BC于H,作直径CF,连接BF.∵∠BAC+∠EAD=180°,∠BAC+∠BAF=180°,∴∠BAF=∠DAE,∴BF=DE,∴==6.A H⊥BC,∴CH=BH,CA=AF,∴AH为△CBF的中位线,∴AH=BF=3.∴点A到弦BC的距离为3.
12.
【解析】
(1)证明:如图1,连接OA、OB,∵OA=OB,∴∠A=∠B.∵=,∴∠AOE=∠BOF在△AOE和△BOF中,,∴△AOE≌△BOF(ASA),∴AE=BF.
(2)如图2,连接OA,∵OM⊥AB,∴AM=AB=6,设OM=x,则OA=ON=x+3,在Rt△AOM中,由勾股定理得62+x2=(x+3)2,解得x=4.5,∴OM=4.5.
素养能力培优
13.D 如图,连接ON、MC、DN,过点O作OE⊥CD交于点E,∵=,∴∠COM=∠COD,故A正确;当OM=MN时,∵OM=ON,∴OM=ON=MN,∴△OMN为等边三角形,∴∠MON=60°,∵==,∴∠COM=∠COD=∠DON,∴∠COD=20°,故B正确:OE⊥CD,∴=,∴=,∴OE⊥MN,∴MN∥CD,故C正确;∵==,∴MC=CD=DN,∵MC+CD+DN>MN,∴MN<3CD,故D错误.
14.【答案】
【解析】如图,作点B关于直线MN的对称点B′,连接AB′交MN于点P′,连接BP′,OB′,OB.∵点B和点B′关于直线MN对称,∴P′B=P′B′,=,AP′+BP′=AP′+B′P′=AB′,易知点P位于点P′处时,AP+BP的值最小.∵点A是上靠近点N的三等分点,点B是的中点,=,∴∠AON=180°÷3=60°,∠B′ON=∠BON=∠AON=30°,∴∠AOB′=∠AON+∠B′ON=90.O A=OB′=1,∴AB′=,故AP+BP的最小值为.
21世纪教育网(www.21cnjy.com)
同课章节目录
