24.3 正多边形和圆精准自测卷(含解析)
文档属性
| 名称 | 24.3 正多边形和圆精准自测卷(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 978.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-14 17:59:36 | ||
图片预览


文档简介
第二十四章 圆
24.3 正多边形和圆
夯基知识梳理
知识点1 正多边形的有关概念及计算全解
1.(2021内蒙古兴安盟中考)一个正多边形的中心角为30°,这个正多边形的边数是 ( )
A.3 B.6 C.8 D.12
2.(2022江苏南京秦淮期末)如图,正八边形ABC-DEFGH中,∠EAG大小为 ( )
A.30° B.40° C.45° D.50°
3.(2022独家原创)如图,平面直角坐标系中,正六边形ABCDEF的顶点A、B在x轴上,顶点F在y轴上,若AB=2,则中心P的坐标为 ( )
A.(2,) B.(1,) C.(2,2) D.(3,2)
4.(2022独家原创)如图,A、B、C、D、E为一个正九边形的顶点,O为正九边形的中心,点P为动点,从点C出发,沿CD向点D运动,在运动的过程中,下列关于∠APB大小的说法,正确的是 ( )
A.始终为20° B.由大变小 C.由小变大 D.由小变大再变小
5.(2021江苏常州武进期中)如图,⊙O的半径为,以⊙O的内接正八边形的一边为边在⊙O内作正方形ABCD,则正方形ABCD的面积为________。
知识点2 正多边形的画法
6.作图与证明:
如图,已知⊙O和⊙O上的一点A,请完成下列任务:
(1)用尺规作⊙O的内接正六边形ABCDEF;
(2)连接BF,CE,判断四边形BCEF的形状并加以证明.
提优强化练习
7.(2021湖南株洲中考,8,)如图所示,在正六边形ABCDEF内,以AB为边作正五边形ABGHI,则∠FAI= ( )
A.10° B.12° C.14° D.15°
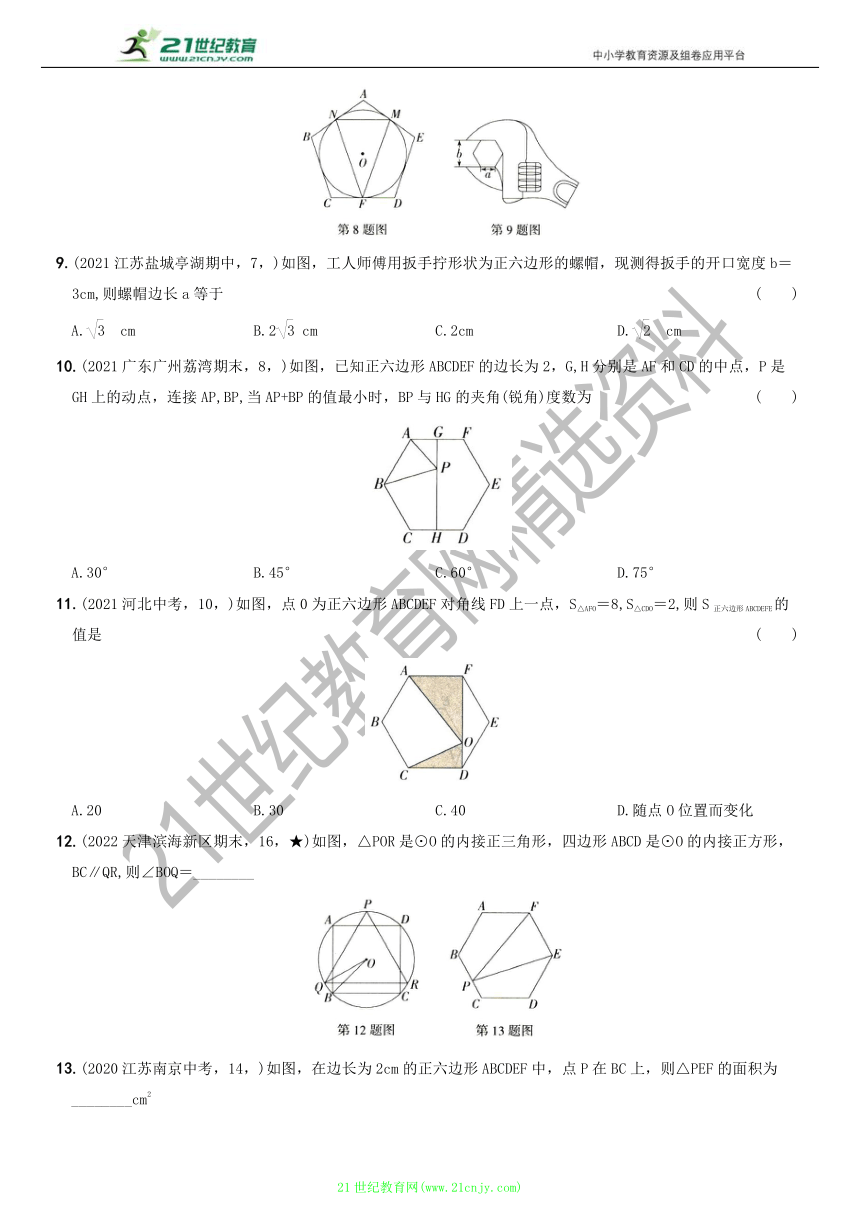
8.(2022福建福州鼓楼月考,9,★)如图,⊙O是正五边形ABCDE的内切圆,点M,N,F分别是边AE,AB,CD与⊙O的切点,则∠MFN的度数为 ( )
A.25° B.36° C.35° D.40°
9.(2021江苏盐城亭湖期中,7,)如图,工人师傅用扳手拧形状为正六边形的螺帽,现测得扳手的开口宽度b=3cm,则螺帽边长a等于 ( )
A. cm B.2cm C.2cm D. cm
10.(2021广东广州荔湾期末,8,)如图,已知正六边形ABCDEF的边长为2,G,H分别是AF和CD的中点,P是GH上的动点,连接AP,BP,当AP+BP的值最小时,BP与HG的夹角(锐角)度数为 ( )
A.30° B.45° C.60° D.75°
11.(2021河北中考,10,)如图,点0为正六边形ABCDEF对角线FD上一点,S△AFO=8,S△CDO=2,则S正六边形ABCDEFE的值是 ( )
A.20 B.30 C.40 D.随点O位置而变化
12.(2022天津滨海新区期末,16,★)如图,△POR是⊙O的内接正三角形,四边形ABCD是⊙O的内接正方形,BC∥QR,则∠BOQ=________
13.(2020江苏南京中考,14,)如图,在边长为2cm的正六边形ABCDEF中,点P在BC上,则△PEF的面积为
________cm2
素养能力培优
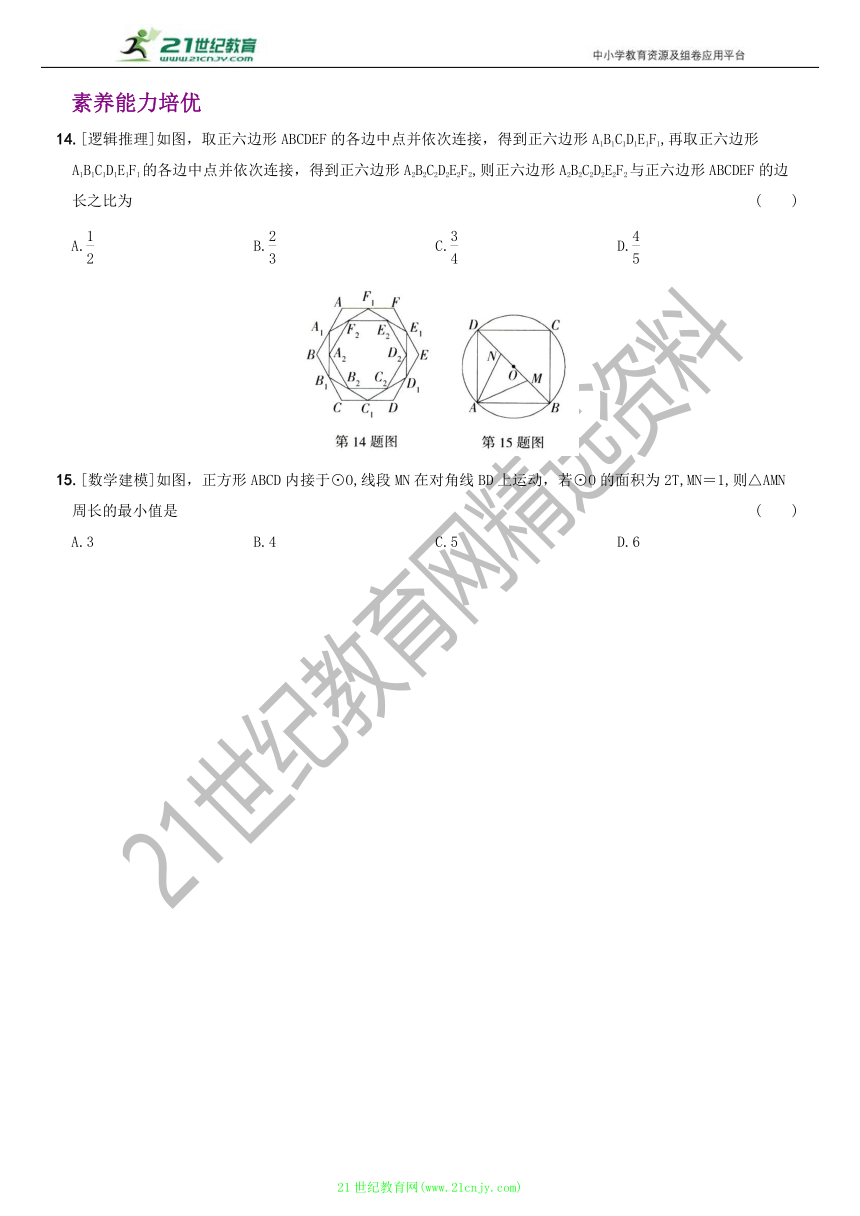
14.[逻辑推理]如图,取正六边形ABCDEF的各边中点并依次连接,得到正六边形A1B1C1D1E1F1,再取正六边形A1B1C1D1E1F1的各边中点并依次连接,得到正六边形A2B2C2D2E2F2,则正六边形A2B2C2D2E2F2与正六边形ABCDEF的边长之比为 ( )
A. B. C. D.
15.[数学建模]如图,正方形ABCD内接于⊙O,线段MN在对角线BD上运动,若⊙O的面积为2T,MN=1,则△AMN周长的最小值是 ( )
A.3 B.4 C.5 D.6
【参考答案及解析】
24.3 正多边形和圆
夯基知识梳理
1.D 这个正多边形的边数==12.
2.C 如图,连接AC、GE、EC,∵正八边形ABCDEFGH的各顶点是其外接圆的八等分点,∴四边形ACEG为正方形,∴∠EAG=45°
3.A 如图,连接PA、PF,作P⊥AB于O,由正六边形的性质可得PF=PA=AF=AB=2,∠APQ=30°在Rt△APQ中,AQ=AP=1,∴PQ==.易证四边形OFPQ是矩形,∴OQ=PF=2,∴点P的坐标为(2,).
4.D 如图,作正九边形的外接圆⊙O,连接OA、OB、AC.由题意得∠AOB==40°,则∠ACB=∠AOB=20°.当点P与点C、D重合时,∠APB=∠ACB=20°,当点P在边CD上且不与C、D重合时,∵点P在圆内,∴∠APB>20°,∴在运动过程中,∠APB由小变大再变小
5.【答案】4-2
【解析】如图,连接OA、OD,过A作AE⊥OD于E,则∠AEO=∠AED=90°,∵∠AOD是正八边形的中心角,∴∠AOD==45°,△AOE是等腰直角三角形,∴AE=OE=OA=1,∴DE=OD-OE=-1,∴AD2=AE2+DE2=1+(-1)2=4-2,∴正方形ABCD的面积=AD2=4-2.
6.【解析】
(1)如图,首先作直径AD,然后分别以A,D为圆心,OA长为半径画弧,交⊙O于点B,F,C,E,连接AB,BC,CD,DE,EF,AF,则正六边形ABCDEF即为所求.
(2)四边形BCEF是矩形.理由:如图,连接OE,∵六边形ABCDEF是正六边形,∴AB=AF=DE=DC=FE=BC,∴===,∴=,BF=CE,∴四边形BCEF是平行四边形∵六边形ABCDEF为正六边形,∴∠EDC=∠FED==120°∵DE=DC,∴∠DEC=∠DCE=30°,∴∠CEF=∠DEF-∠CED=90°,∴四边形BCEF是矩形.
提优强化练习
7.B 在正六边形ABCDEF和正五边形ABGHI中,∠FAB=120°,∠IAB=108°,∴∠FAI=∠FAB-∠IAB=120°-108°=12°
8.B 如图,连接OM,ON.∵M,N分别是AE,AB与⊙O的切点,∴OM⊥AE,ON⊥AB,∴∠OMA=∠ONA=90°.∵∠A=108°,∴∠MON=180°-108°=72°,∴∠MFN=∠MON=36°
9.A 如图,连接AC,过点B作BD⊥AC于D,由题意得∠ABC=120°,AB=BC=a,∴∠BCD=∠BAC=30°,由AC=3,得AD=CD=1.5,∵Rt△ABD中,∠BAD=30°,∴BD=AB=a,∴AD=
=a,即a=1.5,∴a=(cm).故选A.
10.C 如图,连接PF,BF,BF交GH于点P′,连接AP′∵正六边形ABCDEF中,G,H分别是AF和CD的中点,∴直线GH是正六边形的对称轴,∴PA=PF,∴PA+PB=PF+PB.∵PB+PF≥BF,∴当点P与点P′重合时,PA+PB的值最小.∵∠BAF=120°,AB=AF,∴∠ABF=∠AFB=30°.∠FGP′=90°,∴∠FP′G=60°,即∠BP′H=60°.故选C.
11.B 如图,设正六边形ABCDEF的中心为G,连接GC,GD,GE,GF,AC.易得△EFG,△DEG和△CDG都是等边三角形,且大小相同,点C,G,F在同一条直线上,则S△CDG=S△DFG=S正六边形ABCDEF,易得四边形ACDF是矩形,∵S△AFO=8,S△CDO=2,∴S矩形ACDF=2×(8+2)=20,∴S△CDG=S矩形ACDF=5,S正六边形ABCDEF=6S△CDG=30.
12.【答案】15°
【解析】如图,连接OA,OD,OP,∵△PQR是⊙O的内接正三角形,∴PQ=PR=QR,∴∠POQ=×360°=120°.∵BC∥QR,OP⊥QR,∴OP⊥BC.∵四边形ABCD是⊙O的内接正方形,∴OP⊥AD,∠AOD=90°,∴=,∴∠AOP=∠DOP,∴∠AOP=×90°=45°,∴∠AOQ=∠POQ-∠AOP=75°.∵∠AOB=90°,∴∠0OB=15°
13.【答案】2
【解析】如图,连接BF,BE,过点A作AT⊥BF于T,六边形ABCDEF是正六边形,∴CB∥EF,AB=AF,∠BAF=120°,∴S△PEF=S△BEF∵AT⊥BF,AB=AF,∴BT=FT,∠BAT=∠FAT=60°,∴∠ABT=30°,∴AT=AB=1cm,∴BT=cm.∴BF=2BT=2cm,∵∠AFE=120°,∠AFB=∠ABF=30°,∴∠BFE=90°,∴S△PFF=S△BEF=EF·BF=×2×2=2(cm2).
素养能力培优
14.C 如图,连接AF2,设AF1=FF1=a,∵∠BAF=120°AA1=AF1=a,∴∠AF1F2=30°,∠AF2F1=90°,AF2=a,由勾股定理得A1F2=F2F1=a∴A1F1=a.同理可得F2E2=F2F1=a,∴正六边形A2B2C2D2E,F2与正六边形ABCDEF的边长之比a:2a=
15.B 由正方形的性质知,点C和点A关于直线BD对称,如图,过点C作CA′∥BD,且使CA′=1,连接AA′交BD于点N′,截取N′M′=1,连接AM′、CM′,易知A′N′=CM′=AM′,△AMN的周长的最小值等于△AM′N′的周长.连接AC,∵⊙O的面积为2π,∴圆的半径为,则BD=2=AC.∵AC⊥BD,CA′∥BD,∴∠A′CA=90°.在Rt△A′AC中,A′A===3.∴△AM′N′的周长=AM′+AN′+M′N′=AA′+M′N′=3+1=4,∴△AMN周长的最小值是4.
21世纪教育网(www.21cnjy.com)
24.3 正多边形和圆
夯基知识梳理
知识点1 正多边形的有关概念及计算全解
1.(2021内蒙古兴安盟中考)一个正多边形的中心角为30°,这个正多边形的边数是 ( )
A.3 B.6 C.8 D.12
2.(2022江苏南京秦淮期末)如图,正八边形ABC-DEFGH中,∠EAG大小为 ( )
A.30° B.40° C.45° D.50°
3.(2022独家原创)如图,平面直角坐标系中,正六边形ABCDEF的顶点A、B在x轴上,顶点F在y轴上,若AB=2,则中心P的坐标为 ( )
A.(2,) B.(1,) C.(2,2) D.(3,2)
4.(2022独家原创)如图,A、B、C、D、E为一个正九边形的顶点,O为正九边形的中心,点P为动点,从点C出发,沿CD向点D运动,在运动的过程中,下列关于∠APB大小的说法,正确的是 ( )
A.始终为20° B.由大变小 C.由小变大 D.由小变大再变小
5.(2021江苏常州武进期中)如图,⊙O的半径为,以⊙O的内接正八边形的一边为边在⊙O内作正方形ABCD,则正方形ABCD的面积为________。
知识点2 正多边形的画法
6.作图与证明:
如图,已知⊙O和⊙O上的一点A,请完成下列任务:
(1)用尺规作⊙O的内接正六边形ABCDEF;
(2)连接BF,CE,判断四边形BCEF的形状并加以证明.
提优强化练习
7.(2021湖南株洲中考,8,)如图所示,在正六边形ABCDEF内,以AB为边作正五边形ABGHI,则∠FAI= ( )
A.10° B.12° C.14° D.15°
8.(2022福建福州鼓楼月考,9,★)如图,⊙O是正五边形ABCDE的内切圆,点M,N,F分别是边AE,AB,CD与⊙O的切点,则∠MFN的度数为 ( )
A.25° B.36° C.35° D.40°
9.(2021江苏盐城亭湖期中,7,)如图,工人师傅用扳手拧形状为正六边形的螺帽,现测得扳手的开口宽度b=3cm,则螺帽边长a等于 ( )
A. cm B.2cm C.2cm D. cm
10.(2021广东广州荔湾期末,8,)如图,已知正六边形ABCDEF的边长为2,G,H分别是AF和CD的中点,P是GH上的动点,连接AP,BP,当AP+BP的值最小时,BP与HG的夹角(锐角)度数为 ( )
A.30° B.45° C.60° D.75°
11.(2021河北中考,10,)如图,点0为正六边形ABCDEF对角线FD上一点,S△AFO=8,S△CDO=2,则S正六边形ABCDEFE的值是 ( )
A.20 B.30 C.40 D.随点O位置而变化
12.(2022天津滨海新区期末,16,★)如图,△POR是⊙O的内接正三角形,四边形ABCD是⊙O的内接正方形,BC∥QR,则∠BOQ=________
13.(2020江苏南京中考,14,)如图,在边长为2cm的正六边形ABCDEF中,点P在BC上,则△PEF的面积为
________cm2
素养能力培优
14.[逻辑推理]如图,取正六边形ABCDEF的各边中点并依次连接,得到正六边形A1B1C1D1E1F1,再取正六边形A1B1C1D1E1F1的各边中点并依次连接,得到正六边形A2B2C2D2E2F2,则正六边形A2B2C2D2E2F2与正六边形ABCDEF的边长之比为 ( )
A. B. C. D.
15.[数学建模]如图,正方形ABCD内接于⊙O,线段MN在对角线BD上运动,若⊙O的面积为2T,MN=1,则△AMN周长的最小值是 ( )
A.3 B.4 C.5 D.6
【参考答案及解析】
24.3 正多边形和圆
夯基知识梳理
1.D 这个正多边形的边数==12.
2.C 如图,连接AC、GE、EC,∵正八边形ABCDEFGH的各顶点是其外接圆的八等分点,∴四边形ACEG为正方形,∴∠EAG=45°
3.A 如图,连接PA、PF,作P⊥AB于O,由正六边形的性质可得PF=PA=AF=AB=2,∠APQ=30°在Rt△APQ中,AQ=AP=1,∴PQ==.易证四边形OFPQ是矩形,∴OQ=PF=2,∴点P的坐标为(2,).
4.D 如图,作正九边形的外接圆⊙O,连接OA、OB、AC.由题意得∠AOB==40°,则∠ACB=∠AOB=20°.当点P与点C、D重合时,∠APB=∠ACB=20°,当点P在边CD上且不与C、D重合时,∵点P在圆内,∴∠APB>20°,∴在运动过程中,∠APB由小变大再变小
5.【答案】4-2
【解析】如图,连接OA、OD,过A作AE⊥OD于E,则∠AEO=∠AED=90°,∵∠AOD是正八边形的中心角,∴∠AOD==45°,△AOE是等腰直角三角形,∴AE=OE=OA=1,∴DE=OD-OE=-1,∴AD2=AE2+DE2=1+(-1)2=4-2,∴正方形ABCD的面积=AD2=4-2.
6.【解析】
(1)如图,首先作直径AD,然后分别以A,D为圆心,OA长为半径画弧,交⊙O于点B,F,C,E,连接AB,BC,CD,DE,EF,AF,则正六边形ABCDEF即为所求.
(2)四边形BCEF是矩形.理由:如图,连接OE,∵六边形ABCDEF是正六边形,∴AB=AF=DE=DC=FE=BC,∴===,∴=,BF=CE,∴四边形BCEF是平行四边形∵六边形ABCDEF为正六边形,∴∠EDC=∠FED==120°∵DE=DC,∴∠DEC=∠DCE=30°,∴∠CEF=∠DEF-∠CED=90°,∴四边形BCEF是矩形.
提优强化练习
7.B 在正六边形ABCDEF和正五边形ABGHI中,∠FAB=120°,∠IAB=108°,∴∠FAI=∠FAB-∠IAB=120°-108°=12°
8.B 如图,连接OM,ON.∵M,N分别是AE,AB与⊙O的切点,∴OM⊥AE,ON⊥AB,∴∠OMA=∠ONA=90°.∵∠A=108°,∴∠MON=180°-108°=72°,∴∠MFN=∠MON=36°
9.A 如图,连接AC,过点B作BD⊥AC于D,由题意得∠ABC=120°,AB=BC=a,∴∠BCD=∠BAC=30°,由AC=3,得AD=CD=1.5,∵Rt△ABD中,∠BAD=30°,∴BD=AB=a,∴AD=
=a,即a=1.5,∴a=(cm).故选A.
10.C 如图,连接PF,BF,BF交GH于点P′,连接AP′∵正六边形ABCDEF中,G,H分别是AF和CD的中点,∴直线GH是正六边形的对称轴,∴PA=PF,∴PA+PB=PF+PB.∵PB+PF≥BF,∴当点P与点P′重合时,PA+PB的值最小.∵∠BAF=120°,AB=AF,∴∠ABF=∠AFB=30°.∠FGP′=90°,∴∠FP′G=60°,即∠BP′H=60°.故选C.
11.B 如图,设正六边形ABCDEF的中心为G,连接GC,GD,GE,GF,AC.易得△EFG,△DEG和△CDG都是等边三角形,且大小相同,点C,G,F在同一条直线上,则S△CDG=S△DFG=S正六边形ABCDEF,易得四边形ACDF是矩形,∵S△AFO=8,S△CDO=2,∴S矩形ACDF=2×(8+2)=20,∴S△CDG=S矩形ACDF=5,S正六边形ABCDEF=6S△CDG=30.
12.【答案】15°
【解析】如图,连接OA,OD,OP,∵△PQR是⊙O的内接正三角形,∴PQ=PR=QR,∴∠POQ=×360°=120°.∵BC∥QR,OP⊥QR,∴OP⊥BC.∵四边形ABCD是⊙O的内接正方形,∴OP⊥AD,∠AOD=90°,∴=,∴∠AOP=∠DOP,∴∠AOP=×90°=45°,∴∠AOQ=∠POQ-∠AOP=75°.∵∠AOB=90°,∴∠0OB=15°
13.【答案】2
【解析】如图,连接BF,BE,过点A作AT⊥BF于T,六边形ABCDEF是正六边形,∴CB∥EF,AB=AF,∠BAF=120°,∴S△PEF=S△BEF∵AT⊥BF,AB=AF,∴BT=FT,∠BAT=∠FAT=60°,∴∠ABT=30°,∴AT=AB=1cm,∴BT=cm.∴BF=2BT=2cm,∵∠AFE=120°,∠AFB=∠ABF=30°,∴∠BFE=90°,∴S△PFF=S△BEF=EF·BF=×2×2=2(cm2).
素养能力培优
14.C 如图,连接AF2,设AF1=FF1=a,∵∠BAF=120°AA1=AF1=a,∴∠AF1F2=30°,∠AF2F1=90°,AF2=a,由勾股定理得A1F2=F2F1=a∴A1F1=a.同理可得F2E2=F2F1=a,∴正六边形A2B2C2D2E,F2与正六边形ABCDEF的边长之比a:2a=
15.B 由正方形的性质知,点C和点A关于直线BD对称,如图,过点C作CA′∥BD,且使CA′=1,连接AA′交BD于点N′,截取N′M′=1,连接AM′、CM′,易知A′N′=CM′=AM′,△AMN的周长的最小值等于△AM′N′的周长.连接AC,∵⊙O的面积为2π,∴圆的半径为,则BD=2=AC.∵AC⊥BD,CA′∥BD,∴∠A′CA=90°.在Rt△A′AC中,A′A===3.∴△AM′N′的周长=AM′+AN′+M′N′=AA′+M′N′=3+1=4,∴△AMN周长的最小值是4.
21世纪教育网(www.21cnjy.com)
同课章节目录
